双轨火箭橇轨道系统模态及振动特性研究

孙 义,张 琪,赵良玉

(1.北京理工大学 宇航学院, 北京 100081;2.北华航天工业学院, 河北 廊坊 065000)

0 引言

火箭橇是一种可以沿地面固定轨道高速滑行,模拟待测样品高速飞行的地面试验系统[1-6]。由于火箭橇在运行时速度较快,滑块与滑轨之间的碰撞与耦合作用可能会引起滑轨共振,并进而导致滑轨损伤,因此对轨道系统的振动特性进行深入研究是十分必要的。

国内外对火箭橇轨道系统的耦合振动现象均有一定的研究。Laird等[7-8]利用Hydrocode CTH软件针对超音速下的滑车-滑轨撞击过程进行了仿真分析。Yeo等[9]通过建立滑车滑轨撞击的三维有限元模型,系统地分析了滑车-滑轨运行撞击过程中对滑轨产生的热损伤。Lamb[10]通过分析HHSTT滑轨断裂的试验数据,明确了火箭橇滑轨共振是导致滑轨断裂的一个因素,并通过分析弹性波的传播特性,得到了滑轨速度-频率共振通频带,指出火箭橇在特定运行速度下会引起滑轨共振,导致滑轨断裂。张雨诗等[11]以单滑块火箭橇为研究对象,利用ANSYS软件建立了滑轨的简化周期梁模型,进而分析了滑轨的共振特性,仿真得出了0～2 000 Hz频率-速度通频带曲线,指出一定范围的滑车速度及滑车与滑轨的碰撞频率也可能引起共振。余元元等[12]对火箭橇滑轨进行瞬态动力学分析,获得了火箭橇轨道系统对冲击动载荷的响应,并给出了火箭橇在指定速度范围内运行时,滑轨垂向位移和垂向加速度的变化规律。闫华东等[13]以超声速双轨滑车为研究对象,分别基于ANSYS和ABAQUS对滑车的进行模态与强度进行对比分析,总结了2个软件的差异性,以便更好地利用软件进行橇车结构的设计分析。上述研究在建模过程中均对轨道系统进行了不同程度的结构简化,且大都未考虑承轨梁对轨道系统振动特性的影响,为此,建立包含承轨梁的火箭橇轨道系统耦合模型,能够有效地提高计算模型的完整度与仿真结果的可信度。

本文依据真实的火箭橇轨道系统,建立了双轨火箭橇轨道-承轨梁耦合模型,分析了承轨梁对轨道系统固有频率及振动传递特性等的影响规律,为进一步分析滑车和滑轨的耦合振动奠定了基础。

1 耦合模型的建立

1.1 双轨火箭橇轨道系统的三维实体模型

本文所研究的双轨火箭橇轨道系统由滑轨(双)、横向扣件、垂向扣件、H型承轨梁4部分组成。通过三维结构设计软件对轨道系统进行建模,如图1所示。其中,承轨梁长度取15 m,扣件之间距离为0.18 m,每组扣件的间距为1.25 m。

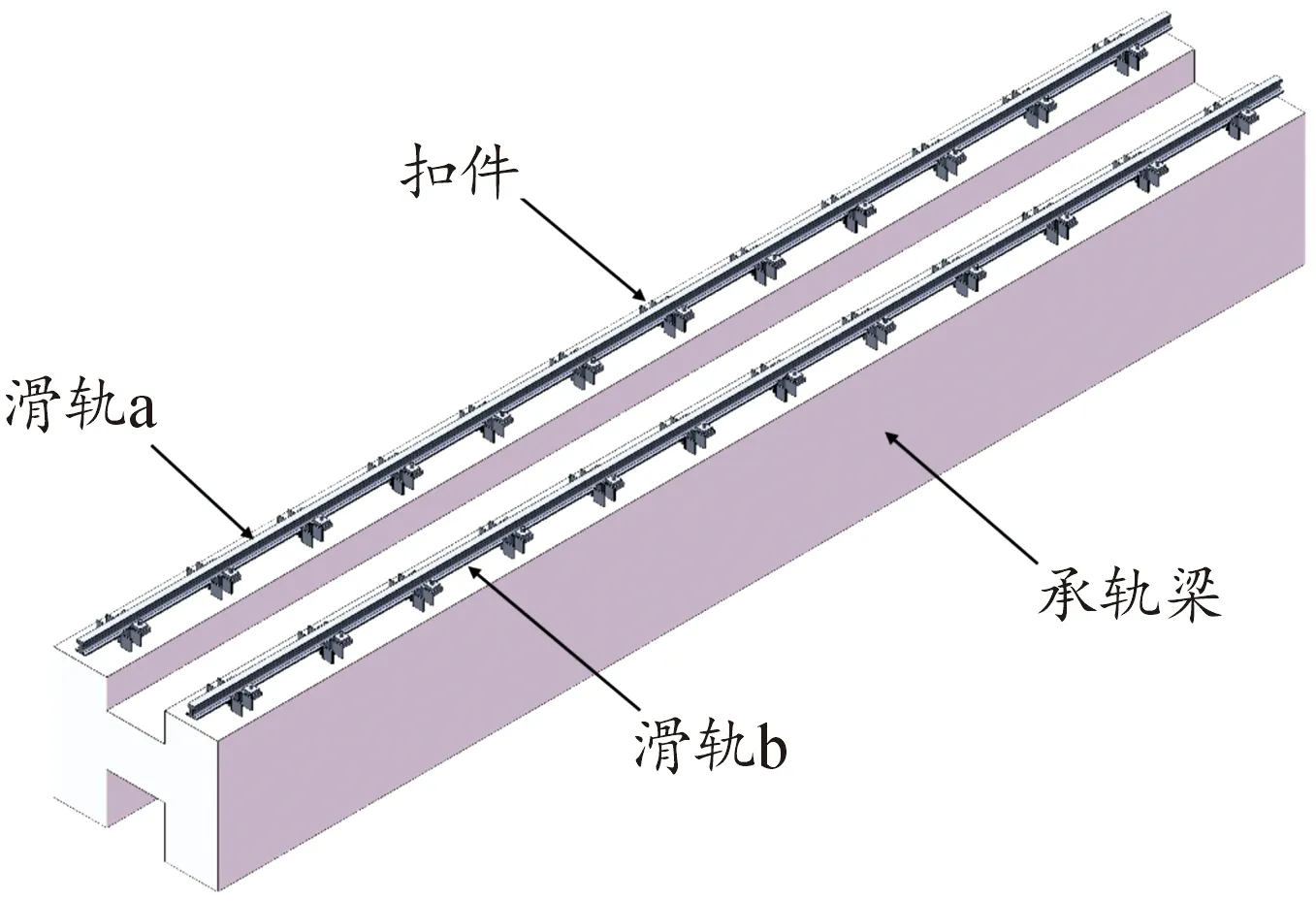
图1 轨道系统的实体模型

1.2 轨道系统的材料属性

滑轨和扣件的材料取为钢,承轨梁的材料设为钢筋混凝土,2种材料的密度、杨氏模量、泊松比及剪切模量等属性如表1所示。

表1 材料参数

1.3 边界条件的确定

考虑到实际情况中扣件与承轨梁、滑轨之间不存在相对滑动,故可将他们之间设为绑定约束;由于每段滑轨之间是通过焊接无缝连结在一起的,可以将其视为一个周期性延长的物体,因此可在每段滑轨两端添加对称约束;承轨梁由4个角上的承台进行支撑,故在其底面的4个角进行固定约束。

1.4 轨道系统网格划分

将上述三维实体模型导入有限元软件ABAQUS[14-15],并对其进行网格划分,网格的单元类型采用C3D8R六面体单元,网格数量为520 007。对承轨梁预埋扣件部分划分较密的网格,其他部分划分较疏的网格以减少计算量,对扣件中较薄的部分划分多层网格,避免刚度失真。垂向扣件、横向扣件、承轨梁和滑轨的网格划分结果分别如图2—图4所示。

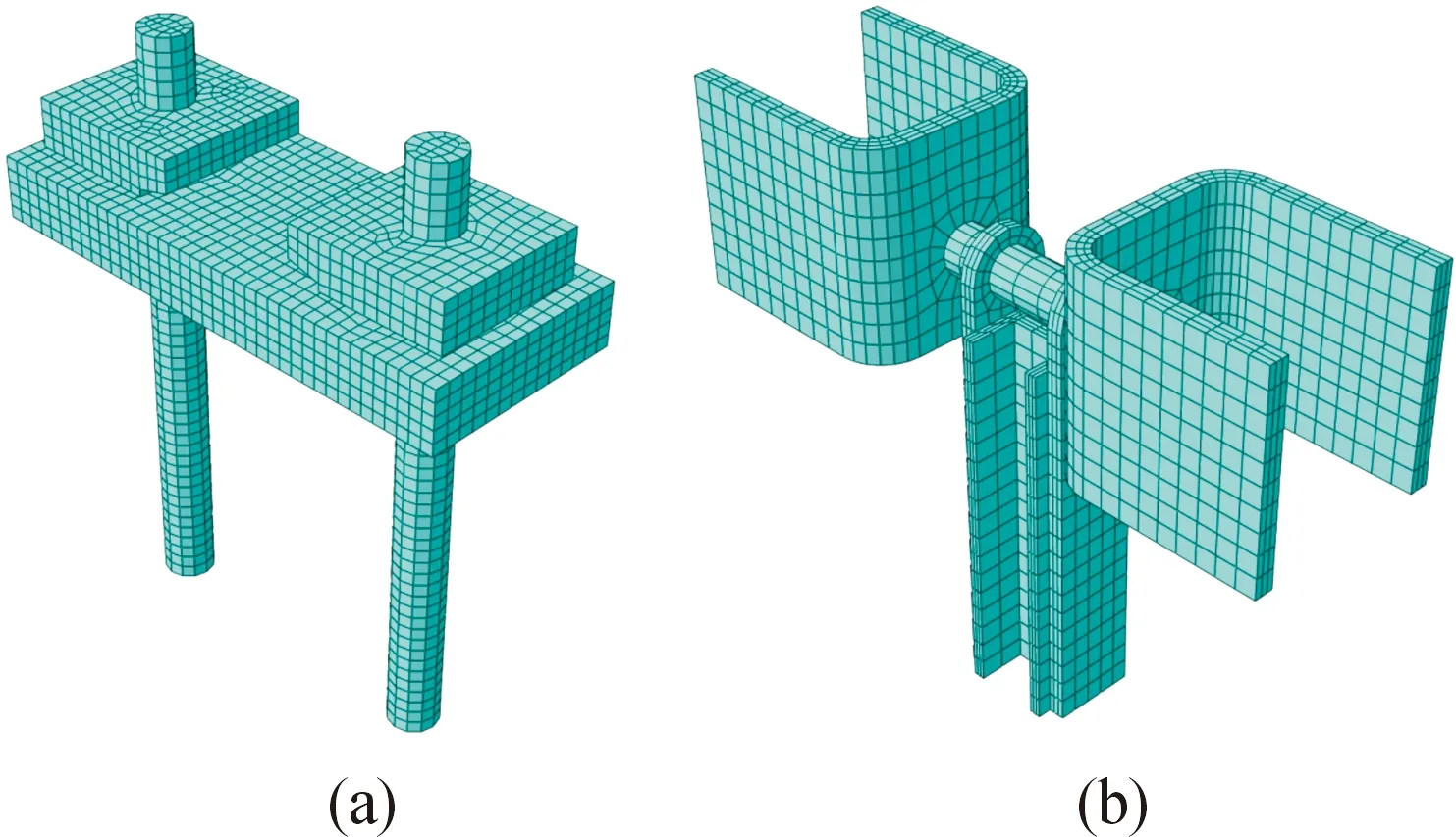
图2 垂向扣件(a)和横向扣件(b)

图3 承轨梁

图4 滑轨

2 模态分析

模态分析是研究结构振动特性的常用手段,通过模态分析,可以提取物体的固有频率和振型等,为避免发生共振现象提供参考[16-17]。此外,为了建立可信的数值模型,需要确保每一部分的模型都在其固有频率范围内。为此,首先对承轨梁、滑轨及扣件开展模态分析。

2.1 承轨梁模态分析

将承轨梁底面的4个角与地面进行固定约束,通过求解可得到承轨梁的频率与振型,前20阶频率如表2所示,第一阶振型如图5所示。

表2 承轨梁前20阶频率

2.2 滑轨与扣件模态分析

将滑轨与扣件之间进行绑定约束,扣件的底部螺柱与地面进行固定约束,计算得到前20阶固有频率,如表3所示。通过分析结构振型,发现侧向一阶弯曲模态的固有频率为188.35 Hz,垂向一阶弯曲的固有频率为303.72 Hz,如图6和图7所示,对比试验数据(见表4),可发现仿真所得固有频率与试验测得固有频率的误差在5%以内,证明所建立的滑轨与扣件模型准确可信。

表3 滑轨与扣件的前20阶固有频率

图6 滑轨和扣件的横向一阶振型

图7 垂向一阶弯曲时滑轨和扣件的振型

表4 模态分析结果与模态试验频率的对比

2.3 轨道系统模态分析

为获得轨道系统的各阶模态,将承轨梁底面的4个角与地面进行固定约束,承轨梁与扣件进行绑定约束,扣件与滑轨进行绑定约束,2条滑轨两端施加Z方向的对称约束,计算得到轨道系统的20阶模态如表5所示,第一阶振型如图8所示。

表5 轨道系统的前20阶固有频率

图8 轨道系统的一阶振型

对比表3和表5中的数据,可以看出承轨梁对轨道系统的固有频率具有较大的影响,因此在滑轨系统建模中不能忽略承轨梁的作用。

3 振动特性影响分析

为探究承轨梁对轨道系统响应特性的影响,对只考虑滑轨和扣件的轨道系统与考虑承轨梁的轨道系统进行数值计算,并通过施加激励的方式,观测滑轨上不同观测点的响应,以探究双轨火箭橇轨道系统的振动特性。

为更加直观地表示振动在滑轨中传递时的变化,引入传递率T的概念,并将其定义为测量值和参考值之比的对数(此处参考值取激励点位置的位移):

(1)

其中:X为测量值;X0为参考值。

3.1 激励载荷大小对振动的影响

为研究激励载荷大小对传递率的影响,对2种工况下的轨道系统进行仿真分析。对于只考虑滑轨和扣件的轨道系统,在滑轨上表面的一端施加正弦激励,激励时间为10 s,周期为π。在激励点、滑轨1/4处、滑轨中间点、滑轨3/4处和滑轨远端点建立相应的观测点,即为观测点1—观测点5(如图9所示)。同理,对考虑承轨梁的轨道系统,在其中一条滑轨上施加相同激励,而另一条滑轨不施加激励。其中,施加激励的滑轨定义为滑轨a,另一条滑轨定义为滑轨b,以同样的方式选取观测点,即为观测点a1—观测点a5、观测点b1—观测点b5。通过改变激励载荷的大小进行仿真,分别取2种工况下滑轨的中间点,即观测点3、观测点a3、观测点b3在Y方向上的传递率进行对比,结果如图10所示。可以看出,激励载荷大小对于2种工况下的轨道系统传递率没有影响。

图9 观测点位置示意图

图10 力的大小对轨道系统传递率的影响

3.2 振动在轨道系统中的传递规律

对于只考虑滑轨和扣件的轨道系统,选取观测点1、观测点3、观测点5在Y方向上的位移变化进行分析,结果如图11所示。可以看出,在施加激励的滑轨上,Y方向上的振幅随着距离的增加而衰减。

图11 滑轨上不同观测点对激励的响应

对于考虑承轨梁的轨道系统,选取观测点a1、观测点a3、观测点a5,以及观测点b1、观测点b3、观测点b5在X方向上的位移变化进行分析,结果如图12、图13所示。

图12 滑轨a上不同观测点的响应

图13 滑轨b上不同观测点的响应

可以发现,在施加激励的滑轨a上,X方向上的振幅随着距离的增加而衰减,滑轨b上传递规律与之相同。对比观测点a1和观测点b1的振幅,可发现振动通过承轨梁传递到另一条滑轨时会产生适当的衰减,这是由于扣件将两条滑轨与混凝土承轨梁绑定在一起,产生了相互的耦合作用。

3.3 承轨梁对轨道系统振动特性的影响

为探究承轨梁对滑轨振动特性的影响。对2种工况下轨道系统的传递率进行分析。

对于只考虑滑轨和扣件的工况,仿真结果如图14所示,X、Y表示相应观测点在X方向和Y方向上的传递率。可以看出,滑轨振动随着激励在轨道的传递而产生衰减,且衰减程度较大。

图14 只考虑轨道和扣件的情况时,各观测点的传递率

对于考虑承轨梁的工况,仿真结果如图15、图16所示。由图可知滑轨的振动随着距离的增加产生衰减,且在X方向上的衰减程度比Y方向上的衰减程度要小。振动在X方向上的衰减趋势是单调的,在Y方向上则有所不同。通过对比图16中滑轨a和滑轨b中各观测点的传递率,可以发现在Y方向上观测点b2、观测点b3的传递率比观测点b1高,这由轨道系统中多个弹性波的叠加引起,但总体来看,此处的传递率较低,对于整体结构的影响较小。

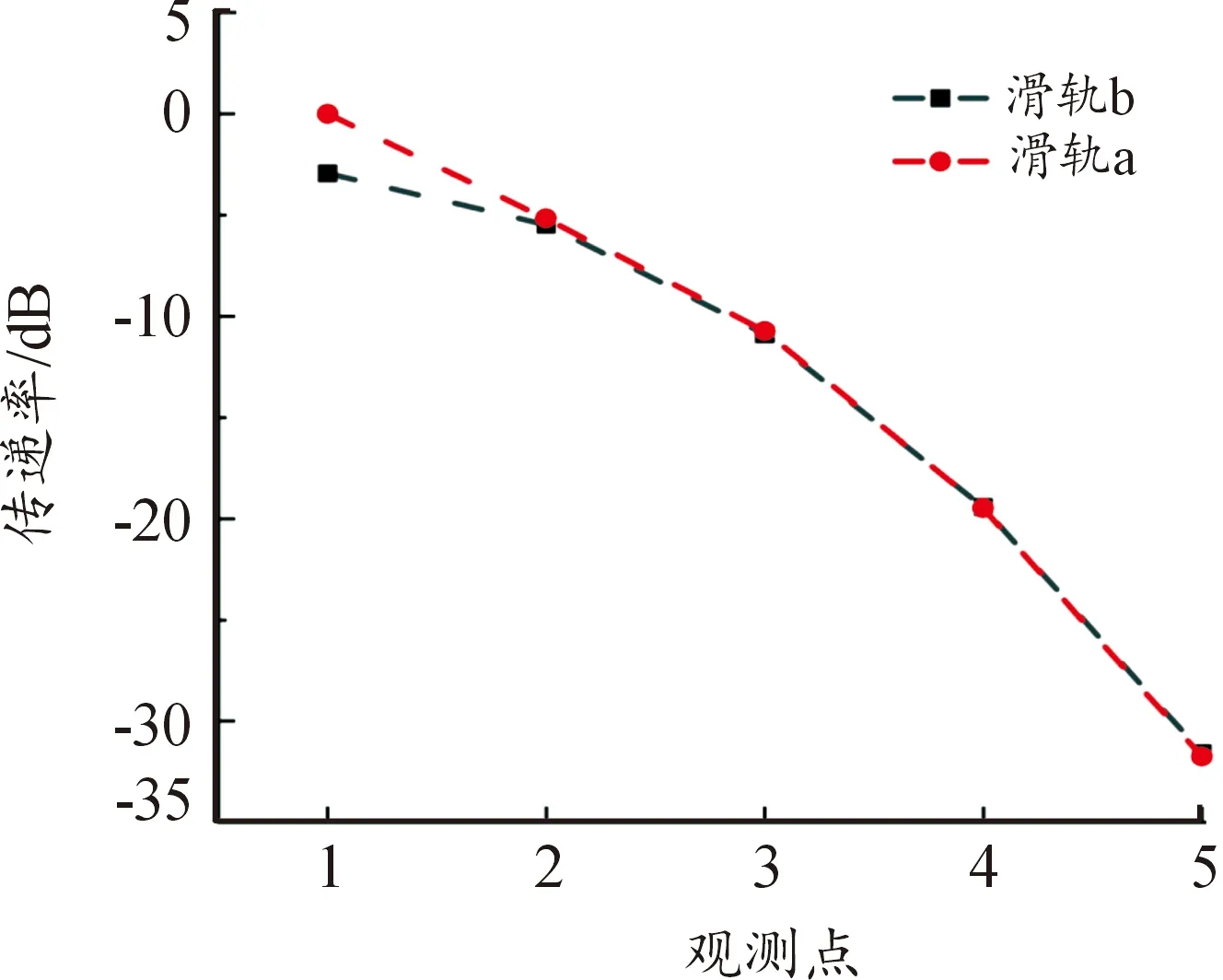
图15 2条滑轨中的观测点在X方向上的传递率

图16 2条滑轨中的观测点在Y方向上的传递率

取激励大小为50 kN时观测点1和观测点a1的Y方向振幅进行分析,如表6所示,可发现承轨梁能有效减小激励点处的振幅,具有良好的减振作用。

表6 不同观测点在50 kN激励下的振幅

4 结论

本文在建立双轨火箭橇轨道-承轨梁三维实体模型的基础上,采用有限单元法分析了承轨梁对轨道系统模态振型、固有频率以及振动传递特性等的影响规律。

1) 建立了双轨火箭橇轨道-承轨梁相互作用的耦合模型,通过模态分析结果与试验测得数据的对比,验证了模型的准确性与可信度。

2) 以轨道-承轨梁耦合模型为基础,探究了承轨梁对轨道系统固有频率的影响,发现承轨梁会大幅降低双滑轨系统的固有频率,在建模过程中不能忽略。

3) 通过引入传递率分析了承轨梁对滑轨振动特性的影响,发现承轨梁可以有效降低激励点处的振幅,具有较好地减振作用。