多环境枪弹高速垂直入水运动特性数值模拟研究

王艺霏,姜伟兵,许 辉,徐化睿,刘亚雷,刘 坤

(1.南京理工大学 机械工程学院, 南京 210094; 2.陆军驻重庆地区第七军代室, 重庆 400000; 3.中国人民武装警察部队海警学院, 浙江 宁波 3158013)

0 引言

传统枪弹侵彻入水后,失去有效杀伤能力,无法对目标造成打击,而多环境枪弹跨介质入水时,利用超空泡技术实现弹头运动减阻,增加弹头有效射程。因此,研究跨介质枪弹入水运动特性对研发新型高效打击枪弹,提高海上作战能力具有重要的军事意义。

枪弹入水过程是由空气进入水中的跨介质过程,该过程涉及介质突变和气液两相耦合,受到了国内外学者的青睐。部分学者[1-2]早期主要集中于低速和垂直入水方面,通过刚性球垂直入水试验,研究了空泡发展、入水弹道和阻力系数等,提出了水花溅射、空泡生成和闭合等概念。随着入水问题的深入研究,国内外学者进一步取得了一定成果。对于刚性球体入水运动,Truscott[3]、Thoroddsen[4]和Holfeld等[5]分别进行了球体入水试验,获得了球体入水过程冲击载荷、空泡形态变化和运动轨迹偏转规律。对于回转体入水方面,国内外主要对弹头形状对入水过程的影响开展了研究。Truscott等[6]对步枪弹小角度入水进行了试验研究,证明了常规步枪弹在水中不能稳定运动;杨衡等[7]、路丽睿等[8]开展了不同形状弹头低速(<6 m/s)入水试验,分析了弹头形状和入水速度对空泡、弹道特性的影响;施红辉等[9-10]研究了钝体、细长体倾斜入水,分析了空泡形成和弹头运动轨迹;侯宇等[11]对超空泡射弹小角度斜入水进行了研究,分析了入水角度对空泡、弹道和弹头结构的影响。可见,现有研究主要集中于锥头圆柱体和大口径超空泡射弹,而对枪弹跨介质入水研究较少。

本文基于56式7.62 mm普通弹,设计一种多环境枪弹,利用ANSYS/LS-DYNA软件,采用流固耦合算法,对该枪弹高速垂直入水过程进行数值模拟,通过与常规步枪弹入水过程数值模拟结果对比,分析多环境枪弹入水过程、空泡形态和弹道性能。研究成果可充实弹药设计理论,为武器优化提供理论参考。

1 有限元模型的建立

1.1 有限元模型

本文参考56式7.62 mm普通弹外形,提出了一种7.62 mm口径的多环境(multi-environment ammunition, MEA)枪弹结构方案,以适用于陆上/水下多环境作战,实现跨介质杀伤,枪弹结构如图1所示,枪弹基本参数如表1所示。多环境枪弹弹头分为弧形部、圆柱部和尾部,尾部开有倒角,弧形部采用平头多梯度锥体加空化槽的特殊结构,圆柱部增加多个环槽,提高稳定性,该外形促进了弹头入水后气泡生成,减少了水与弹头的接触面积,降低了粘性阻力,实现弹头的水下减阻增程。

图1 枪弹模型Fig.1 Bullet model

表1 枪弹模型参数Table 1 Bullet parameters

1.2 材料模型

弹头材料为钢,侵彻入水过程受到应变率、损伤等多因素的影响,将产生塑性变形,选用*MAT_JOHNSON_COOK模型进行描述,该材料模型广泛应用于弹道侵彻冲击、金属爆炸成型等数值计算。Johnson-Cook模型本构关系表示为[12]:

(1)

熔化无量纲温度可表示为:

(2)

式中:Tr为室温;Tm为熔化温度。

Johnson-Cook模型通过损伤参数D描述损伤度,可表示为:

D=∑Δεp/εf

(3)

式(3)中:Δεp为等效塑性应变增量;εf为材料失效应变。

材料失效应变εf可表示为:

(4)

式中:D1、D2、D3、D4、D5为损伤参数;σ*为压力与等效应力σeff的比值(σ*=p/σeff)。Johnson-Cook材料模型参数如表2所示。

表2 Johnson-Cook材料模型参数Table 2 Projectile material parameters

水和空气选用*MAT_NULL模型,均采用EOS_GRUNEISEN状态方程,可通过该方程定义其压力体积的关系,从而确定材料的压缩状态。状态方程可表示为:

(5)

式中:p为材料压力;E为材料的内能;c为冲击波速度-质点速度Hugoniot曲线的截距;S1～S3为曲线的斜率;γ0为Gruneisen系数;μ为体积变化率;a是和μ的一阶体积修正量。

水和空气具体参数如表3所示。

表3 水和空气参数

1.3 网格划分

为研究弹头侵彻入水过程,采用ALE算法进行流固耦合计算,设置空气和水域为无反射边界条件,避免入水后冲击波在空气域和水域模型边界反射对求解产生影响。

仿真计算时,引入如下假设:

1) 将弹丸视作整体且入水后不旋转。

2) 水为不可压缩、无旋、有势、不计粘性的流体。

3) 忽略重力影响。

考虑数值模拟的计算效率和计算量,采用二分之一模型,取水域和空气域宽度为弹头直径的10倍,空气域为8 cm×4 cm×3 cm,水域为8 cm×4 cm×40 cm,设置为对称边界,以保证观测到完整空泡形态和初始冲击波的传播。在弹头与水域的直接接触区及附近划分网格较密,网格尺寸与弹头单元尺寸相近,与接触区域较远处采用相对较粗的网格。分别采取不同密度进行网格划分,将数量为86万网格和120万网格进行仿真结果对比,计算结果误差不高于2%。考虑到计算效率,本文采用86万网格进行仿真计算,弹头网格数量为1 900,水域网格数量为68万。有限元网格模型如图2所示。

图2 网格划分模型Fig.2 Grid division model

2 结果分析

本文通过弹头高速垂直入水数值模拟,分析7.62 mm口径MEA枪弹在750 m/s初速下垂直入水时的空泡形态和弹道变化规律,并与56式7.62 mm普通弹垂直入水仿真结果进行对比。

2.1 有限元算法验证

为验证模型算法和参数的正确性,通过文献[14]中圆柱体入水实验得出的理论公式与采用本文有限元算法计算的平头圆柱弹入水结果进行对比,当射弹以603 m/s初速垂直入水,弹头直径为12.66 mm,长度为25.4 mm,所得速度时间、位移时间曲线如图3所示。从图3可知,仿真所得速度与位移变化情况与文献[14]一致性较好,误差小于4%,验证了有限元算法的可行性。

图3 仿真结果与理论结果对比Fig.3 Comparison between simulation results and theoretical results

2.2 枪弹流场结构特性和空泡形态变化

枪弹入水过程可分为冲击、流动形成、空泡航行及全湿航行等4个阶段,本文主要研究冲击、流动形成和空泡航行阶段弹头的运动特性。在入水冲击阶段,弹头以高速冲击水面,较短时间内经历了由空气到水介质的突变,弹头与水相互作用,能量迅速传至弹头附近水域。附近水域将获得的能量转化成远离弹头表面方向的动量,形成了惯性扩张力,导致弹头流动分离形成,此时能量耗损主要用于排开弹头周围流体,形成空泡,弹头的动能转化成周围水质点的动能。

图4为MEA枪弹垂直入水后不同时刻液相的压力云图。由图4可知,弹头入水初期(1～20 μs),产生了一个较大的冲击波在水中传播并逐渐衰减,随着弹头进一步与水面接触,冲击波幅值逐渐变小,弹头弧形部附近始终处于高压区状态;弹尖完全入水后(20～50 μs),弹头空化槽附近出现低压区,随着入水深度不断增加,空化槽后低压区域不断扩大,最后包裹弹尖部分,这是空化槽处形成的涡旋现象导致,涡旋使局部流速加快,局部压力降低。弹头入水时,弹尖首先与水面发生撞击,压力迅速增大至峰值,弹头弧形部前方高压区域靠近弹体位置压力较高,压强峰值出现在弹头弧形部中点区域,高达100 MPa。

图4 入水压力变化云图Fig.4 Cloud image of entry pressure variation

MEA枪弹和56式7.62 mm普通弹以750 m/s初速垂直入水时,不同时刻空泡图如表4所示。由表4可知,MEA枪弹入水50μs时,弹头入水距离约1.5倍弹长,弹尖采用的多梯度锥体结构促进流动分离,在弹头弧形部出现较为明显的流动分离,空泡包围弹体和尾部且不发生接触;100 μs时,空泡最大直径趋于稳定,弹体附近的空泡形态基本保持不变,空泡最大直径为28.01 mm,约弹径的3.5倍。56式7.62 mm普通弹50 μs时,弹头垂直进入水面,入水距离约1.5倍弹长,形成对称空泡,由于弹体形状流畅光滑,空化效果差,空泡内部产生雾化液滴;100 μs后,空泡最大直径逐渐稳定,弹体附近的空泡形态基本保持不变。弹体后部空泡区域不断增大,弹体周围空泡扩张程度低,空泡壁面与弹头接触,并逐渐向弹尾方向移动,空泡不能完全包围住弹体,使弹头直接接触到液体产生扰动,导致弹道失稳,其产生的空泡最大直径18.1 mm,约弹径的2.3倍。

综上所述,通过对比可知,MEA枪弹和56式7.62 mm普通弹入水空泡形态差异较大,常规步枪弹入水空化程度低,空泡壁面轮廓不清晰,空泡内雾滴较多,对空泡形态破坏明显;MEA枪弹入水后产生的空泡形态对称,空泡壁光滑,内部无液滴生成,空化程度较高,与常规步枪弹相比,空泡直径更大,空泡分离点更稳定。

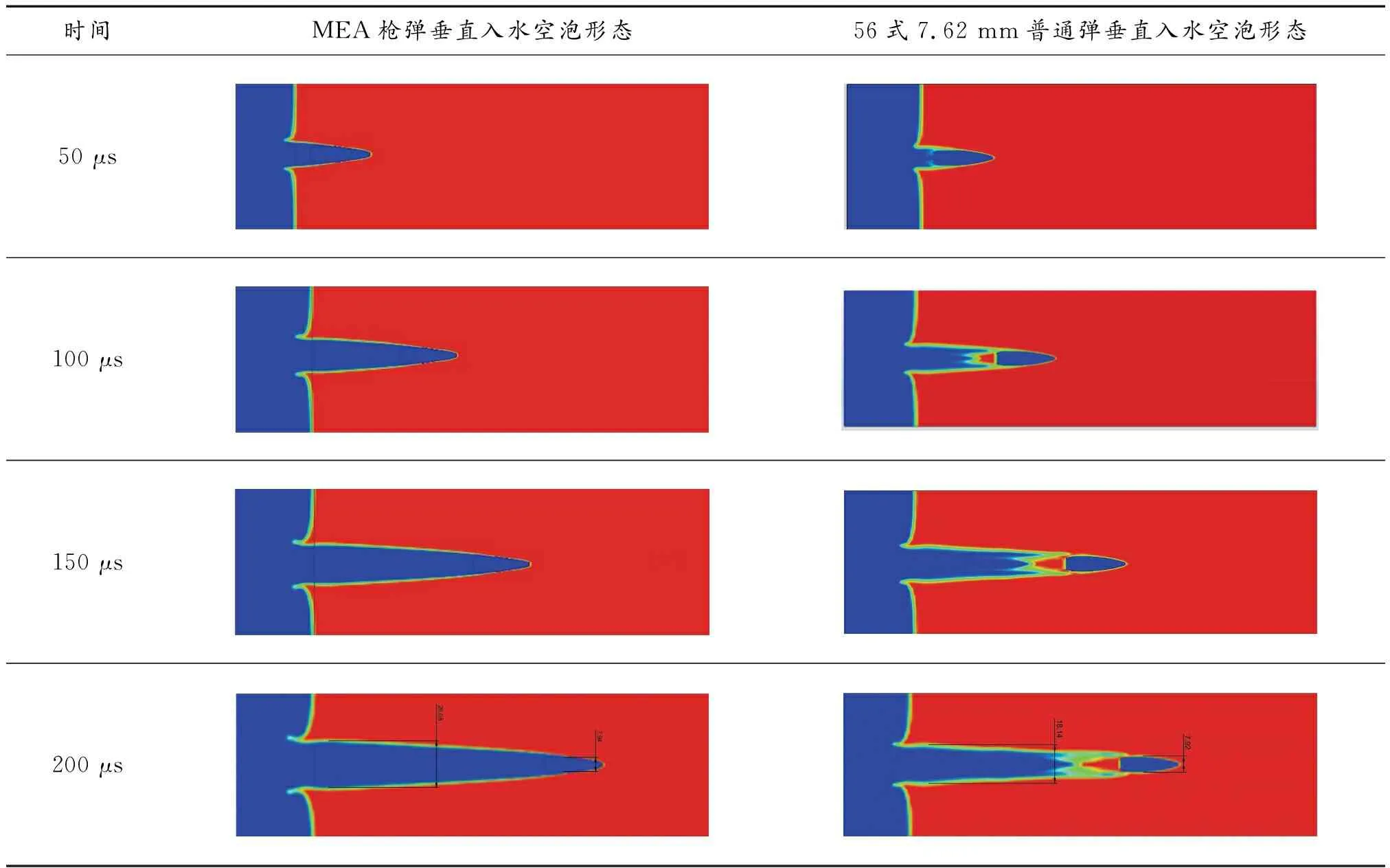
表4 2种弹丸垂直入水空泡图Table 4 Cavitation diagram of two projectiles entering water vertically

2.3 入水过程运动规律分析

MEA枪弹和56式7.62 mm普通弹在初速为750 m/s垂直入水时,弹头速度随时间变化规律如图5所示,图6为2种枪弹入水后侵彻距离随时间变化规律。由图5、图6可知,由于常规步枪弹外形较为光滑,对流场扰动能力弱,入水过程中弹头传递给周围流域的动量低,使前期速度衰减较慢;50 μs后,弹头全部入水,由于弹头产生的空泡空化程度低,弹体与水产生接触,其运动过程所受阻力增大,速度衰减加快。由于MEA枪弹在弹头弧形部增加了空化槽,入水初期发生局部流域增速,入水过程中弹头传递给流域的动量降低,在弹头全部入水后,产生稳定的空泡包裹弹体,弹头不会与液体产生直接接触,速度衰减变慢。在400μs时,MEA枪弹速度为678.9 m/s,位移为28.6 cm;常规步枪弹速度为534.1 m/s,位移为25.3 cm。与常规步枪弹相比,MEA枪弹入水400 μs后,存速能力提高了19.3%,侵彻位移增加了13%,相较常规步枪弹起到了减阻增程的效果。

图5 MEA弹与常规步枪弹入水速度变化Fig.5 Variation of water entry velocity between MEA projectile and standard projectile

图6 MEA弹与常规步枪弹入水深度变化Fig.6 Variation of water entry depth between MEA projectile and standard projectile

3 结论

本文基于56式7.62 mm普通弹,设计了一种MEA枪弹,通过ANSYS/LS-DYNA软件对其入水过程开展了数值模拟,分析了MEA枪弹高速垂直入水时空泡形态、弹道轨迹与流体动力特性变化规律,并与常规步枪弹入水仿真进行了对比,得到以下结论:

1) MEA枪弹入水产生冲击波,随着弹头不断接触水面,冲击波幅值逐渐变小,高压区始终在弹头弧形部附近,空化槽有利于降低局部压力,弹尖入水后空化槽周围出现低压区,且低压区逐渐扩张包裹住弹头。

2) MEA枪弹多梯度斜锥体的弹形设计比常规步枪弹更利于产生流体分离,常规步枪弹入水空化程度低,空泡壁面轮廓不清晰,而MEA枪弹入水产生的空泡壁面光滑,空化程度高、空泡直径更大和空泡分离点更稳定。

3) 相同初速垂直入水情况下,入水400 μs后,MEA枪弹相较常规步枪弹存速能力提高19.3%,侵彻位移增加13%,减阻增程效果明显。