基于混频Lamb波的闭合裂纹定位方法仿真

孟佳颖,郑慧峰,凌田昊,赵 娜

(1. 中国计量大学计量测试工程学院,浙江 杭州 310018;2. 中国特种设备检测研究院,北京100029)

1 引言

金属材料由于其良好的物理性能、化学性质和工艺性能,在航空航天、国防军工和机械制造等领域得到了广泛的应用。但在使用过程中,金属材料受到长时间的载荷作用,必然会出现材料性能的退化和内部微观组织结构的损伤,给整个设备的安全性和可靠性带来巨大的风险,因此要尽早对其中可能存在的缺陷进行检测[1]。常规的Lamb波检测技术基于线性传播理论,利用反射透射系数等传播参数来对材料内部缺陷进行检测,然而闭合裂纹的尺度在微米级,远小于波长量级,对于反射透射等特性的影响不明显,无法使用常规Lamb波检测技术进行检测。基于非线性传播理论的混频Lamb波检测技术则可以克服上述缺陷,对闭合裂纹进行有效检测[3]。

混频Lamb波检测技术是一种将非线性混频方式与超声Lamb波技术相结合的检测技术[4]。通过选取合适的入射频率和入射角度,可使产生的混频波沿着理想的方向传播,能够给大型金属板结构中早期损伤的检测带来便利。并且非线性混频方法可以解决非线性超声检测中二次谐波不足的问题,有着对早期损伤灵敏度高的优势。

目前对混频检测技术结合导波形式来进行检测的研究还比较少,主要分布在两块:对非线性混频导波条件的理论推导;针对混频条件验证及混频导波信号分析的仿真研究。本文将在此基础上对共线混频Lamb波检测技术进行研究。在理论推导方面,李卫彬等人[5]讨论了两个基频兰姆波产生二阶和三阶组合谐波的内共振条件,并预测了在不同混频频率下二阶和三阶组合谐波的存在。在仿真研究方面,Han Chen等[6]研究了两个不同频率的反向传播Lamb波在双层板中引起的频率混合响应模型,并数值模拟和分析了界面性质对混频效应的影响。Hasanian等[7]针对局部材料退化损伤,利用有限元仿真手段分析混频信号并对退化程度进行了表征。焦敬品[8]以数值仿真和实验的方式对板中疲劳裂纹进行了非线性Lamb波混频检测,结果表明混频波能够有效检测出板中疲劳裂纹。Feilong Li等[9]用数值模拟的方法研究了薄板中混频二阶非线性Lamb波的传播。

本文利用有限元软件对对向共线混频Lamb波检测技术进行仿真,对生成的混频Lamb波进行了验证,确定其有效混频范围,应用混频Lamb波检测技术分析了不同尺寸的闭合裂纹对非线性参数的影响,探究非线性参量对闭合裂纹表征的可行性,并对铝板中闭合裂纹进行了检测与定位。

2 基本原理

2.1 混频Lamb波理论

混频Lamb波的基本理论如图1所示,两个基频波信号从不同方向入射,在板结构中某处相遇,当两Lamb波满足混频发生的“共振条件”时,就可以产生具有累积效应的混频波了[5]。

图1 对向共线混频示意图

当板状材料出现微损伤时,其材料结构会随之发生改变,使之成为弱的各向同性板。弹性波在弱各项同性、均匀的非线性弹性材料中传播的运动方程为

(1)

其中u为力学位移,λ和μ为二阶弹性系数,ρ为材料的初始质量密度,F(u)为与u相关的非线性项。考虑到两个平板导波“a”和“b”在板状材料中沿着相同方向传播,则运动方程的位移场接通过摄动近似法分解得到与基频波相关项(ua和ub)、自作用的相关项(uaa和ubb)和相互作用的相关项(uab),具体如下所示[7]

u=ua+ub+uaa+ubb+uab

(2)

对于平板导波在x方向传播,基频波的位移解可以写成以下形式

ua(x,z)=Re{ua(z)ei(kax-ωat)}

ub(x,z)=Re{ub(z)ei(kbx-ωbt)},

(3)

其中k和ω分别代表波数和角频率,并且k值可正可负。将基频波位移解ua和ub的实部代入到各项同性材料的Landau-Lifshitz应变能函数,得到包含指数函数的项

ei((ka±kb)x-(ωa±ωb)t),e-i((ka±kb)x-(ωa±ωb)t),ωa≥ωb

(4)

这些指数函数项在(ωa+ωb,ka+kb)和(ωa-ωb,ka-kb)处符合对应的二次谐波项,即分别是和谐波和差谐波。

2.2 混频超声非线性系数

目前二次谐波法是非线性超声检测中研究最多、应用最广、检测技术最为成熟的方法,根据相关文献可知,材料的二阶非线性声学系数

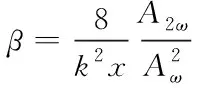
(5)

(6)

其中k1、k2分别为频率为ω1和ω2的波数。对于频率和相速度确定的基频波以及传播距离x确定的条件下,为了便于测量和计算可以采用相对非线性参数β′=Aω2±ω1/Aω2Aω1评价材料的疲劳损伤程度。

2.3 闭合裂纹定位理论

非线性混频Lamb波除了能够检测闭合裂纹,还需要对结构中的闭合裂纹进行准确定位,通过控制两列基频波激发时间延时的方式可以进行结构的线扫查,以此来确定闭合裂纹的位置。

若在t=0时刻激励左侧基频波a,将右侧基频波b进行t=Tdb延时激励,则二者相遇时间为

(7)

其中L为板的长度,Cga和Cgb分别为基频波a、b的群速度。此时,两列基频波发生混频的位置到板的左端点的距离l为

l=Cgat

(8)

将(7)式代入(8)式可得混频位置与基频波b延时激励时间的函数关系表达式为

(9)

同理可得对左侧基频波a进行t=Tda延时激励的情况。分析式(9)可知,如果分别使两列基频波的激励延时时间逐渐增加,则能使混频位置存在板水平方向任意区域,从而实现利用混频Lamb波对整个结构的线扫查。通过对板进行粗略的扫查,观察板中各处接收到的信号中是否存在混频波,即可初步判断出闭合裂纹的存在区间。对该区间进一步细化扫查,应用前述推导的式(6)可对区间内各处的损伤程度进行评价,当非线性系数超过某一阈值时即可判断为闭合裂纹存在,否则可认为该处板材是无损的。

3 仿真研究

3.1 对向共线混频Lamb波仿真

在COMSOL中建立如图2所示的二维模型,该模型尺寸为800mm×3mm,材料为上节铝合金6061。两个基频Lamb波S模态信号加载采用端面方式加载,在试件侧边处施加指定面内位移模拟激励信号所选择的Lamb波的模态,激发出的Lamb波信号比较纯净且可以避免端面反射和反对称模式影响。激励信号源均为汉宁窗调制正弦信号,根据混频波生成的“共振条件”,选取源u1为0.8MHz的30周期,源u2为1.8MHz的50周期,如式(10),指定位移的幅值均为10-4mm,等同于几个MPa量级的应力,与实际固体中超声应力相等[12]。选择在瞬态研究下进行分析,总时长是根据两个基频Lamb波信号群速度计算出合适的分析时长10-4s,此时两个信号均不会在端面产生反射信号。

图2 对向共线混频Lamb波仿真示意图

当两基频信号的中心完全重合时,可认为两基频信号完全混频,使两基频信号完全混频的位置称为混频的中心点,混频的中心点位置取决于两基频信号的群速度、板长以及两基频信号时域波包长度等因素。通过计算可知,两列基频Lamb波u1、u2将在板中300mm处完全重合并发生混频,则可以在该处设置信号接受点去分析是否产生2.6MHz的和频二阶谐波u3。

取x=300mm处的面内位移信号进行频域特性分析,如图3所示。从图中可以清楚看到基频频率项0.8MHz和1.8MHz、和频频率项2.6MHz以及基频二倍频项3.6MHz等。由此可认为两基频Lamb波信号在x=300mm处发生相互作用产生混频信号。

图3 300mm处面内位移信号频响曲线

3.2 有效检测区域分析

为确定混频Lamb波的有效检测区域,需要对板上各处接收信号进行分析。根据接收信号中混频波的有无,可确定两基频波相遇后的大致混叠区域在240mm～320mm之间。为进一步确定有效混频区域,可以在该范围内以10mm等距设置采样点接收各个位置的时域信号,并进行FFT变换得到该范围内的频谱图。从各个信号的频谱中提取混频二阶谐波的幅值和两个基频谐波的幅值,计算非线性系数β′并进行归一化处理,结果如图4所示。

图4 不同位置非线性系数图

从图中可以看出不同位置的混频波非线性系数的变化情况,依据非线性系数的变化趋势可将该区域划分为三段,第一段即x=300mm右侧部分,混频波非线性系数大幅度减小,可认为该范围内混频信号即将分开,说明这一区域不在有效混频区范围内;第二段即x=260mm～300mm部分,此范围内混频波非线性系数大幅度增加,且可以观察到积累效应,说明两基频波混频程度逐渐增强,这一区域位于有效混频区域范围内;第三段即x=240mm～260mm,混频波非线性系数存在上下波动情况,说明此时两基频波刚好开始相遇进行混频过程,混频信号存在不稳定增长状态。由此可确认实际具有积累效应的有效混频区范围为x=260mm～300mm。

3.3 闭合裂纹检测模拟

为了确定共线混频Lamb波检测技术能够对接触类损伤进行检测及评价,Lamb波混频信号还需对材料中接触类损伤有很高的敏感度。在ABAQUS有限元仿真软件中研究两基频Lamb波与闭合裂纹相互作用产生混频非线性效应进行分析,二维仿真模型如图5所示,模型设置与前述基本相同,为避免材料非线性对研究的影响,铝合金6061的材料属性设置为为线性弹性材料,闭合裂纹设置在x=290mm,处于前述验证的两基频波有效混频范围内,模型中闭合裂纹形状为矩形,长度设置为2mm,宽度设置为0.05mm,接触条件为硬接触、无摩擦。

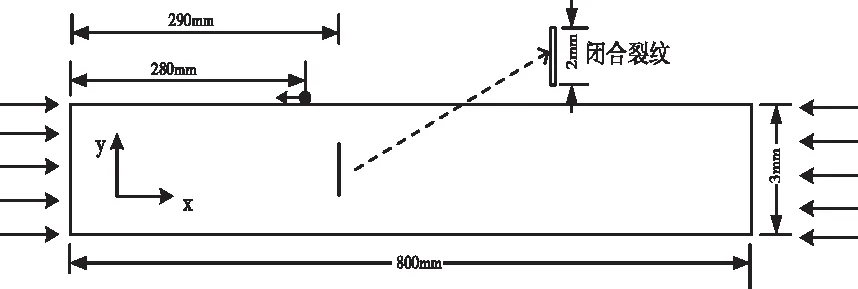
图5 含微裂纹铝板有限元模型图

当闭合裂纹位于混频波的有效范围时,若两基频波在混叠区域与闭合裂纹发生非线性效应,则在闭合裂纹左侧的接收面内位移信号中将会存在混频信号。同时设置另一无闭合裂纹的有限元模型进行对比,在相同信号接收点不能检测出混频信号,即可证明混频信号的产生需要接触类损伤存在,且对其十分敏感。在上述有限元模型设置完毕基础上开始混频Lamb波检测仿真,分别在后处理模块上提取面内位移信号输出,将两个信号通过FFT变换进行分析,结果如图6所示。

图6 有无裂纹模型信号对比图

从图6中可以观察到无闭合裂纹模型的信号中只存在两个基频波信号和谐波信号,而存在闭合裂纹模型中除之前所述的信号外,额外存在混频生成的2.6MHz和频信号。因此可以确定混频Lamb波能够检测板中存在的闭合裂纹。

4 仿真结果分析

4.1 闭合裂纹表征

在确定混频Lamb波能够检测板中存在的闭合裂纹后,进一步研究混频信号对闭合裂纹演化的响应情况。分别研究闭合裂纹的长度和宽度对产生的混频分量的影响,进行了具有不同长度和宽度闭合裂纹板中混频Lamb波检测有限元仿真。图7所示为带通滤波后两种情况下得到的不同损伤程度下的混频时域信号。

图7 混频信号对闭合裂纹演化的响应变化

从图中可以看出,当闭合裂纹的宽度固定时,混频信号的幅值随着闭合裂纹的长度增加而增加;当闭合裂纹的长度固定时,混频信号的幅值随之闭合裂纹的宽度增加而减小。将两种情况下的接收信号进行FFT变换后,分别计算不同损伤程度下的相对非线性声学系数β′。其结果如图8所示。

图8 非线性声学参量随裂纹尺寸变化关系

由图可知,闭合裂纹产生的非线性效应与闭合裂纹尺寸密切相关。随着闭合裂纹的长度增加,非线性声学系数β′也会增大,当裂纹长度小于1mm时,非线性系数对闭合裂纹长度变化敏感较低,当裂纹长度大于等于1mm时,随着长度的不断增加,非线性系数也急剧增大,可认为是裂纹界面的接触刚度呈现减小趋势,使得非线性效应增强。另一方面,随着闭合裂纹的宽度增加引起了非线性系数β′的减小,当裂纹宽度小于等于0.1mm时,非线性系数对闭合裂纹宽度变化比较敏感;当宽度大于0.1mm时,随着宽度的增加非线性系数以幅度较小的趋势降低,即此时对闭合裂纹宽度变化不敏感,可认为随着闭合裂纹宽度的增加,使得界面发生非线性效应所需要的激励幅值增加,从而导致混频的激发效率降低,非线性系数呈减小趋势。综上所述,可认为利用混频Lamb波信号追踪及评价材料中的闭合裂纹是可行的。

4.2 闭合裂纹定位

为对闭合裂纹进行定位,采用线扫查方式对有效混频区域进行扫查。对左基频波a分别施加2.6×10-4s和5.2×10-4s的时延,混频中心会随之移动至x=260mm和280mm处对附近进行探测,依此调整基频信号的延时并在相应混频中心位置处接收混频信号,对接收到的混频Lamb波信号进行FFT变换以得到混频信号的频域特征。图9为混频中心点移动不同距离处接收到的频域信号。

图9 不同混频中心的接收信号频域图

从图中可以看出,混频中心移动到x=280mm、x=300mm的接收信号中可以观察到明显的和频信号存在,而在其它混频中心的接收信号中均未观测到和频信号的存在,说明闭合裂纹大致存在于x=280mm～300mm之间。若要进一步确定闭合裂纹的尺寸信息,可以通过细化两基频波的激发时延去对x=280mm～300mm部分继续扫查。使混频中心以4mm的步长在该范围内移动,图10为不同混频中心点接收信号计算出的非线性系数分布。

图10 非线性系数定位分析图

从图中可以明显看出x=284mm和288mm处的非线性要大于其余三处位置,以该范围内非线性系数最大值的60%作为闭合裂纹存在的判断阈值,即图中红虚线。可认为在该阈值上是大概率存在闭合裂纹的,在该阈值下的位置是完好的,因此闭合裂纹在结构中大致位置是在x=284mm～292mm。

5 结论

1)本文基于有限元软件建立了二维铝板的材料模型,选取了模式对为0.8MHz的S0信号和1.8MHz的S0信号混频生成2.6MHz的S2信号,证明了共线混频Lamb波技术的可行性。

2)在有限元中应用混频Lamb波方法检测板中闭合裂纹,成功识别到了损伤信号,对不同尺寸的闭合裂纹进行了检测和表征,并用线扫查的方式对其进行了定位。