一种直接上升式轨道转移计算仿真方法

吴启星,赵灵峰,王 涛

(1. 北京跟踪与通信技术研究所,北京 100094;2. 中国科学院微小卫星创新研究院,上海 200120;3. 中山大学智能工程学院,广东 广州 510006)

1 引言

轨道交会是指两个运行在不同轨道上的航天器在空间某点彼此接近的过程。通常在轨运行的航天器并不需要进行轨道交会,甚至是要避免轨道交会。但是,随着空间技术的不断发展以及空间应用领域的拓展,轨道交会正逐渐成为许多空间任务执行过程中的重要环节,例如在轨服务[1]、天基空间目标监视等[2]。为了提高空间任务的执行效率,在有限末制导修正能力约束条件下实现在轨多目标快速交会显然非常有意义,尤其是针对不在同一轨道平面上的多颗卫星[3-6]。王伟林等[7]研究了在轨航天器不同约束条件下航天器交会追踪区、遭遇区的优化求解方法。韩威华等[8]研究了有限推力轨道转移与交会组合优化设计问题,给出一种基于时间最优的转移和交会模型。吴蓓蓓等[9]针对空间可交会目标数量与轨道转移所需的脉冲速度增量等约束条件提出了一种平台停泊轨道设计方法,并给出了优化分析模型。

本文提出了一种基于有限某修正能力的直接上升式轨道转移优化设计方法用于目标交会轨道设计,通过转移轨道约束条件的分析、转移轨道的设计方法以及转移轨道优化选择的标准分析,给出了空间飞行器快速直接上升式轨道交会计算方法。

2 轨道转移设计方法

空间飞行器采用直接上升轨道转移的方式实现快速空间交会,需要对轨道转移的约束条件进行分析,图1为轨道直接上升轨道转移空间交会几何示意图。

图1 交会几何条件示意图

约束条件:

1) 空间飞行器应与目标同时到达某一点,这一点即为预计交会点,且位于目标轨道上;

2) 假设空间飞行器在中末制导段作惯性飞行,空间飞行器助推加速是通过助推器一次点火完成,则空间飞行器在点火点的待增速度应小于助推器的视速度增量;

3)考虑到飞行器接近目标的末制导段采用可见光导引,因此在转移轨道的末段,进入导引头工作范围内时,目标星应在光照区内。

基于三个可交会约束条件,给出初制导段(助推点火段)的转移轨道设计方法如下:

1)选择目标轨道上的一段区域作为有效交会区域,选取一定的步长,对该区域进行搜索,并对其中的每一个预计交会点遍历。

2)每一个预计交会点同时又能对应找到空间飞行器驻泊轨道上的一系列可允许的转移区域。对这些可允许转移区域也进行搜索,选取一定的步长对其中的每一个可转移点进行遍历。

3)如果某一个预计交会点所对应的的转移点所需待增速度最小,则将其视为准最优转移点。

4)在所有预计交会点所对应的准最优转移点中,寻找所需代增速度最小的转移点。如此,经过对有效交会区域和可允许转移区域的两次遍历,最终能找到一对最佳预计交会点(位于目标轨道上)和最佳转移点(位于飞行器驻泊轨道上)。

5)最佳预计交会点(位于目标轨道上)和最佳转移点之间的转移轨道,即是设计得到的转移轨道。

上述计算步骤如图2所示。图中的目标在近地点附近出发,沿其轨道顺时针方向运动。空间飞行器在近地点附近出发,沿其轨道逆时针方向运动。有效交会区域中的两个预计交会点A1和A2分别对应空间飞行器的可转移点D11,D12及D21,D22。如果空间飞行器在这四个点中的某个点进行轨道转移时所需待增速度最小,就将其作为最佳转移点TD＿Optimal,对应的预计交会点作为最佳预计交会点TA＿Optimal,二者之间的转移轨道即是设计得到的转移轨道。

图2 有效交会区域与可转移区域示意图

3 轨道转移计算

1) 真近点角fd的取值范围

由于空间飞行器与目标要同时到达预计交会点,所以需要分析空间飞行器的转移点在转移轨道上真近点角的取值范围。转移轨道为椭圆,转移点和预计交会点分别为D(xd,yd,zd)和A(xa,ya,za)。这两点到地心的向径分别为rd、ra,满足

(1)

其中,a为转移轨道的椭圆半长轴,e为偏心率。fd、fa分别为D点、A点在转移轨道上的真近点角,并有

fa=fd+Δf

(2)

其中,Δf满足式

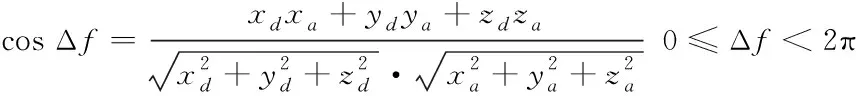
(3)

2) 满足时间约束的转移区域确定

设飞行器与目标的初始状态(位置、速度)已知,将目标轨道上的一点Aj作为预计交会点,目标由初始点飞行至该点的时间为taj;平台轨道上的Di点为转移点,平台由初始点飞行至该点的时间为tdi。则交会时间约束条件可写成

taj=tdi+tdi＿aj

(4)

其中,tdi＿aj为空间飞行器从转移点飞行至预计交会点的时间。

3) 满足速度增量约束的有效转移区域确定

由于采用液体燃料助推,燃烧时间可以随意进行控制。在空间飞行器满载质量和助推器燃料质量已知的情况下,由式(5)可以计算得到液体动能飞行器的视速度增量Δvs

(5)

其中,Isp为助推发动机比冲,m0为空间飞行器点火时刻质量,mF为助推发动机燃料质量。

将视速度增量Δvs与每个可允许转移区域的最小待增速度Δvdi＿aj＿min相比较,若有

Δvdi＿aj＿min≤Δvs

(6)

则表明一定可以从该可允许转移区域中找到一条转移轨道,使得空间飞行器沿着该转移轨道飞行时,既满足交会时间约束条件,助推器所提供的速度增量也能够满足待增速度要求,因此可以在该可允许转移区域中选取转移点。反之,则表明从该可允许转移区域中任何一点Di分离后飞往预计交会点Aj,尽管可以找到满足交会时间约束条件的转移轨道,但这些转移轨道在转移点Di处的待增速度始终大于助推器所能提供的速度增量,因此最终的转移点不能在该可允许转移区域中选取。

如果区域最小待增速度ΔvD＿aj＿min比视速度增量Δvs还大,则表明对于预计交会点Aj来说,不能在驻泊轨道上找到任意一个区域作为空间飞行器的有效转移区域,必须重新选择预计交会点的位置。

4 轨道优化选择算法

通过以上分析,可以找到既能满足时间约束条件又能满足待增速度限制的有效转移区域。对找到的k个有效转移区域再分别进行小步长Step＿m(m=1,…k)划分,而后对每个有效转移区域进行搜索,得到转移点Valid＿Dmi(m=1,…k,i=1,…n) 进行遍历。对Valid＿Dmi计算满足时间约束条件的转移轨道,并记下对应的待增速度增量ΔvDmi＿Aj。比较这m×n个待增速度,可以找出一个最小待增速度ΔvD＿Aj＿min。因此对于预计交会点Aj,也就找到了满足时间约束条件下最小待增速度最小的准最佳转移点Valid＿D＿Aj。

在目标有效交会区域内沿目标前进方向将目标轨道划分从而改变预计交会点,重复以上寻找有效转移区域和Valid＿D＿Aj的步骤,可以找到在目标有效交会区域内不同预计交会点对应的Valid＿D＿Aj。由于采用液体助推,为节约助推燃料,需要使待增速度尽量小。因此设定性能指标J满足

J=ΔvD＿Aj＿min

(7)

如果能使J达到最小,那么最佳预计交会点A＿optimal和最佳转移点D＿optimal也就确定下来了。然后根据这两点求出最优的一条转移轨道。

1) 确定转移时间和初始姿态

空间飞行器的转移诸元包括助推器点火时刻和点火过程中的姿态角。在最佳转移点、最佳预计交会点和最优转移轨道确定后,计算转移诸元。

已知飞行器的待增速度为ΔvD＿Aj＿min,空间飞行器在助推发动机工作前的初始质量为m0,得到助推发动机工作消耗燃料如下

(8)

因此,助推发动机工作时长为

(9)

其中,F为助推发动机推力大小。

设td时刻空间飞行器在转移点D处分离,当td≤t≤td+tf时,助推发动机点火,其余时间关闭。

然后是转移时初始姿态角的计算。设td时刻转移点D处的空间飞行器待增速度Δv在地心惯性系中的各方向分量分别为Δvx、Δvy、Δvz。根据弹体坐标系与地心惯性坐标系之间的转换关系,可以得到

(10)

将式(10)展开并进一步整理后,可以得到转移诸元中的偏航角ψc和俯仰角ϑc如下式所示

(11)

当对飞行器弹体Y1轴和Z1轴指向无特殊要求时,可设定转移诸元中的滚转角γc为任意角度(一般取为零)。

5 仿真结果

不加入误差参数,在理想情况下进行数学仿真,获得一些重要的仿真数据包括转移轨道的轨道根数、空间飞行器的转移诸元以及空间飞行器与目标的最小相对距离时刻、燃料消耗量等。仿真数据如下所示,其中涉及到时间的量均是按照初始时刻为0开始计算的。飞行过程中的仿真结果如图3和图4所示。

图3 飞行器与目标星的轨道高度

图4 飞行器姿态变化情况

在不加误差的情况下,分别改变目标的近地点幅角和轨道倾角的大小,考察空间飞行器在不同目标情况下的制导控制效果,从而验证了本设计方法的有效性。表中位置偏差(D)、助推剩余燃料(mT)、轨控剩余燃料(mo)、姿控剩余燃料(mA)。

从表1～2可以看出,改变目标空间轨道的初始位置分布,空间飞行器在满足时间约束、光照条件约束和能量最省约束条件的情况下,通过制导控制算法后得出相应的控制指令对空间飞行器进行制导飞行,达到了同目标交会的要求,位置偏差在2m～4m之间。

表1 同步卫星目标近地点幅角(ω)变化时最终仿真结果

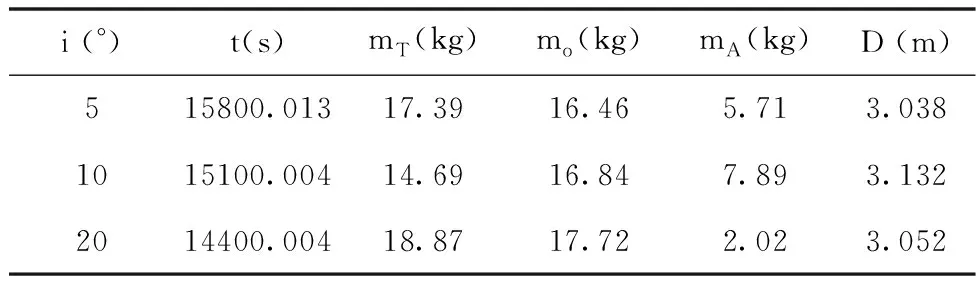
表2 同步卫星目标轨道倾角(i)变化时最终仿真结果

6 结论

随着空间应用领域的拓展,对空间飞行器的在轨交会能力需求越来越大。本文正是针对空间飞行器在有限末制导修正能力的基础上快速直接上升交会的实际需求,提出了一种直接上升式交会轨道设计优化选择方法。该方法突破了传统的共面交会轨道设计思想,有效解决飞行器与目标航天器快速交会问题提供了技术途径,具有较大的现实意义和广阔的应用前景。