经纱张力调节机构的拓扑优化设计与疲劳分析

赵全鹏 杨建成 刘艳哲 黄子文

摘 要：为提升经纱张力调节机构的动态补偿能力，适应三维间隔织物剑杆织机的高速化织造需要，引入可吸收应力的变刚度气动肌腱作为原动件，设计了一种新型经纱张力调节机构。采用有限元技术对该机构进行了静力学分析和模态分析，得到其静态特性及前六阶固有频率阵型，在此基础上采用变密度法对机构进行拓扑优化，随后根据优化结果在SW中进行结构优化并采用有限元仿真实验进行验证。结果表明：拓扑优化后的机构可以减重13.32%，同时应力、应变和固有频率等静动态性能均有较大提升，其最小疲劳寿命可达17.91年，满足织机使用年限的需要。最后在VSI系列样机上进行了对比实验，分析优化前后的张力采样曲线。实验结果表明优化后的织机经纱张力波动更加平稳，机构动态特性有效提升。

关键词：张力调节机构；拓扑优化；轻量化设计；模态分析；疲劳寿命分析

中图分类号：TS103.3

文献标志码：A

文章编号：1009-265X（2023）03-0027-09

基金项目：国家科技支撑计划重点项目（2011BAF08B02）

作者简介：赵全鹏（1998—），男，山东潍坊人，硕士研究生，主要从事纺织机械设计制造及自动化方面的研究。

通信作者：杨建成，E-mail：18222663096@163.com

织机送经系统的主要功能是按照织物结构对纬密的要求，以合适的送经量送出织造所需要的纱线；依据设置的上机张力，运用自身的运动来保持经纱张力的稳定，调节其它运动因素所引起的张力波动［1］。随着织机的高速化和智能化发展，间隔织物织机对送经系统的动态补偿能力提出了更高要求。间隔织物织机较常规织机具有特殊性，其具有两条用于织造层纱的地经和一条实现织物“站立”与层纱交织的绒经，三者相耦合组成整个间隔织物织机送经系统，每个送经机构分成三部分：送经轴部分、张力补偿机构、张力检测装置。张力调节机构是送经系统中实现动态补偿功能的部分，是实现送经功能的核心。

对于织机送经系统的完善与发展，国内外学者和工程人员付出了诸多努力。周东波［2］对送经系统的机械构件分别进行了整体和局部静力学分析研究，提出了相应的改进措施；王斯勇［3］建立了送经机构结构参数与性能间的联系，并深入探讨了不同织造工况下结构参数的调整方向；武银飞等［4］阐述了电子送经机构基本原理与组成，为送经机构的结构参数设计提供了参考方案；郑宝平等［5］详细分析了送经系统中张力调节的摆动性能及其对送经系统性能的具体影响，并运用几何知识将各个参数建立了联系，为电子送经系统的创新和优化奠定了理论基础；Kim等［6］建立了送经机构静力学和动力学模型，设计了单后梁的送经机械结构。

综合以上研究现状可知，现有的研究基本都是针对二维织物织机所进行的，二维织物织机和三维织物织机具有明显的差别，三维间隔织物剑杆织机送经机构较普通织机有如下特点：新增的实现织物“站立”的绒经对开口的幅度有较大要求，所设计送经机构应具备更高的动态张力调整能力，以应对较大的张力波动［7-10］；织物织造时速度在较高区间，送经系统应具有灵敏的响应性能［11-12］。因此研究三维间隔织物织机的经纱张力调节机构具有重要的实际意义。本文将对三维间隔织物织机经纱张力调节机构进行设计与优化。

1 经纱张力调节机构的设计

三维织机结构复杂，且工作时每个组织循环综框的动程是变化的，因此对调节机构的响应性和精确度提出了更高要求。现有张力调节机构的原理是运用变刚度气动肌腱驱动摆动双后梁实现对张力的调整，在张力检测和控制系统配合下控制张力波动在合理范围内。其所具有的反应速度快、调节力度可控的优势契合三维间隔织物织造需要。气动肌腱作为原动件，实现了精简机构，切实提高机构的运动精度和响应性能［13-16］。气动肌腱是仿照肌肉的自然运动而制成，由可伸缩管道和接头组成，可伸缩管道由橡胶膜片及表面的无弯曲纤维构成，膜片用于密封气体，纤维用于传递强度与力。气动肌腱的静态特性为f（p，ε，F）=0，则其单根肌腱的刚度特性如式（1）所示。通过改变内部气压可获得不同的刚度，在织造过程中可实时控制气压以适用不同织造工况，其功率重量比大，单位截面积输出力是单作用气缸的8倍以上。此外，气动肌腱具有阻尼性，可以缓冲减震，提高了送经的精确度。

式中：K为气动肌腱刚度，N/m；ΔF为输出力变化量，N；Δl为伸缩量，m；F为输出力，N；ε为收缩率；p为气动肌腱容腔内绝对压力，Pa。

所设计机构的三维模型中，固定后梁作为回转中心，其芯轴通过轴承安装在织机墙板上，摆臂将固定后梁和活动后梁芯轴联结为一体，气动肌腱与摆臂之间采用销钉铰接，气动肌腱驱动力通过摆臂精确传递，同时活动后梁外工作面与芯轴用轴承装配，保证经纱张力调节的顺利进行，最大限度地确保了织造三维织物时机构的动态特性。

2 张力调节机构的拓扑优化设计

为了验证所设计张力调节机构的可靠性，提升机构的静、动态力学性能以适应三维织物的织造需要，对机构进行了有限元静力学分析、模态分析，并在此基础上进行了拓扑优化，合理的轻量化设计使结构更加可靠。

2.1 机构有限元分析

运用Workbench中的Static Structural模块对机构进行极限工况下的仿真分析。

a） 创建机构的有限元模型

采用自下而上的建模方式，先建立张力调节各部件模型，然后生成整個机构的有限元模型。所建立的有限元分析模型如图1所示。

b） 机构各零件材料设定

基于对机构整体质量和其运动特性的考虑，同时兼顾连接强度和成本，选定各结构的材料。固定块和后梁的芯轴选用综合力学性能较好的45号钢，摆臂选用强度高和疲劳性能强的7075铝合金，气动肌腱作为原动件其外壳材料选择Carbon fiber。各材料的力学性能参数如表1所示。

c） 模型网格划分

网格划分时运用整体自动划分网格与关键零部件细化网格相结合的方法。网格划分之初，对比了网格尺寸7、5、3、1 mm几种情况，结果表明随着网格划分的细密，仿真时最大位移值和最大应力数值将收敛于精确值，但运算速度随之下降，为了兼顾求解速度和结果准确度，将网格大小设定为3 mm，划分后单元格数为105896，节点数目为259359，网格质量均值0.769，大于0.7，能达到较好效果。机构网格划分如图2所示。

d） 极限工况的载荷施加

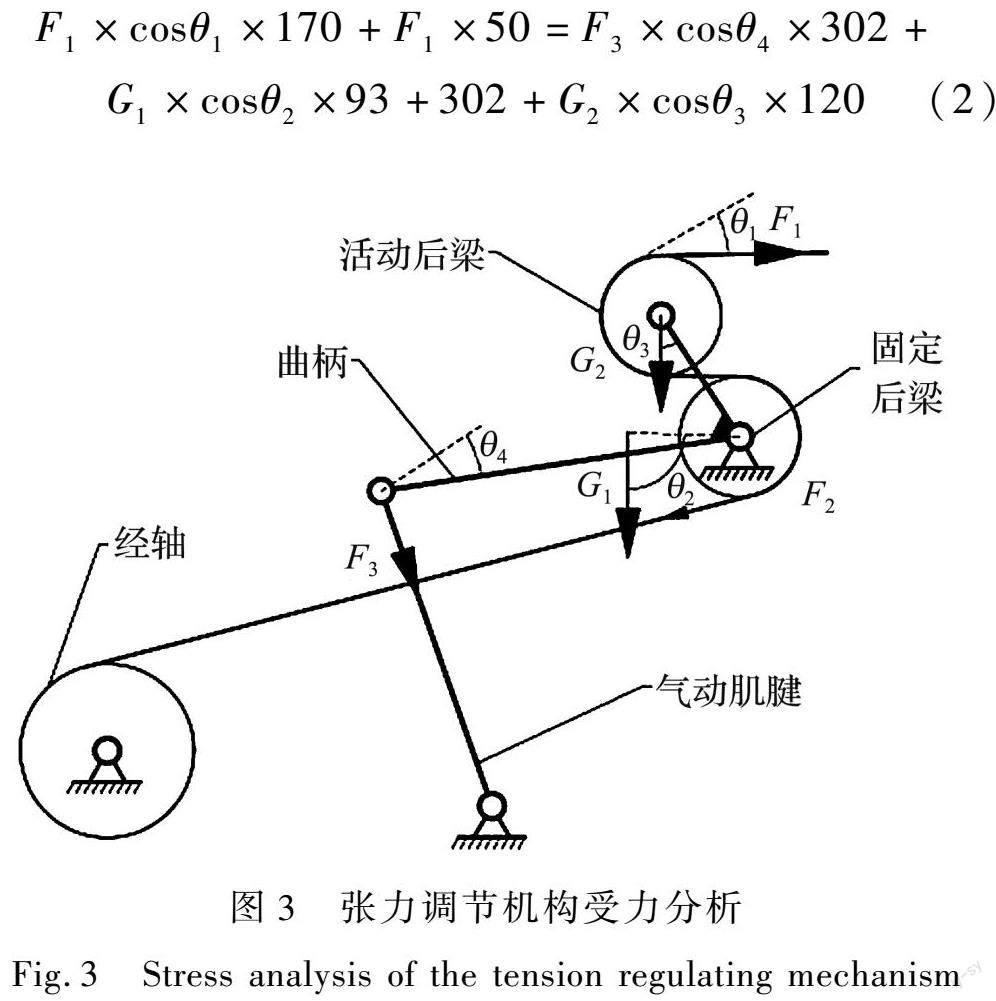
机构的驱动件是气动肌腱，从动件为摆臂，先通过受力分析确定张力调节机构极限工况时的载荷状态。机构的受力分析如图3所示，图3中F1、F2、F3分别为活动后梁上经纱张力、固定后梁处张力、摆臂所受气动肌腱的推动力，G1、G2分别为摆臂自重、活动后梁自重。

以摆臂为研究对象，建立力矩平衡方程式（2）。

极限工况时经纱张力F1为最大单根经纱张力与经纱根数的乘积，而最大单根经纱张力50 g，该三维织机经轴的单层经纱容纳量为4200根，故F1在极限工况下数值为2058 N。此时θ1、θ2、θ3和θ4分别为12°、109°、14°、12°。将以上各参数代入式（2）得F3=1419 N。得到极限工况下的载荷后，分解后施加在已建立模型中，具体约束条件与载荷如图4所示。

e） 机构静力学求解

对机构进行静力学求解后，后处理得到张力调节机构的最大变形云图和等效应力云图，如图5与图6所示。

由图5可知，张力调节机构最大变形发生在固定块与气动肌腱连接处，极限载荷工况下最大变形数值为0.8198 mm，如此的变形量对张力调节整体的性能影响不大，只需对连接处材料厚度处理即可，机构有较大的减重空间。

由图6可得，张力调节机构最大等效应力发生在摆臂与气压肌腱连接过渡的位置，最大等效应力值为4.859 MPa，远小于7075铝合金的屈服强度值505 MPa，故不会发生疲劳失效的状况，可以进一步减重以达到轻量化目标。

2.2 张力调节机构模态分析

张力调节机构受到纱线施加给的周期性激励，加之其自身的经纱调节运动也是周期性的，二者会产生周期性的振动。因此需进行模态分析掌握其固有频率特性，避免激振源与机构产生共振发生失效。图7为利用Workbench中的Modal模块解算出机构模态前六阶固有频率云图，由图7可知一阶固有频率为0，六阶固有频率最大，其值为1.503×10-3 Hz。

本文所研究的三维剑杆织机完整工作周期是0.1 s，周期内有两个峰值，分别为打纬运动与开口运动所产生。两峰值之间的间隔是10/36周期，由此可得该织机工作频率为36 Hz。同时，机构是安装在织机墙板上，需要考虑织造时机构与墙板发生共振的频率。对样机墙板进行共振测试后得其共振频率值是44.5 Hz［17］。张力调节机构前六阶固有频率与织机工作频率以及墙板共振频率之间差值巨大，机构在织造过程中发生共振的概率极低，其动态特性符合三维剑杆织机织造需要，故可以进一步轻量化。

2.3 变密度法拓扑优化设计

由静力学求解结果可知，经纱张力调节机构各项机械性能指标在极限载荷下仍具有较大的减重空間。为了在轻量化设计的基础上最大程度地提升刚度，在保证相同的载荷和约束条件，采用变密度法在有限元分析的基础上对机构进行拓扑优化。

a） 拓扑优化数学模型

优化区域是张力调节机构，设计变量为区域内相对单元材料密度，定义域设置为［0，1］，约束条件设置为最大应力和最大应变，模型的目标函数为最小重量，数学模型表达为：

式中：ρ为设计变量，c（x）是目标函数，V为计算区域体积，E（ρ）表示ρi弹性模量，P是惩罚因子，E0为实际弹性模量，M*是优化后重量上限，n为计算区域单元数。

为了缩短迭代的次数，最大限度提高收敛速度，本文基于目标函数的性质，引进了新的参数g改进此模型，每次迭代后所得的密度再参与该运算，如式（4）所示：

式中：g0和Δg分别为g的初始值和增量，γ和c*分别是强度因子。

需要注意的是，c*的选用合理与否会影响目标函数和模型收敛的速度［18-21］。

b） 拓扑优化的过程与结果分析

首先将拓扑优化模块链接到静力学分析结果。在拓扑优化的前处理中，选择优化区域为经纱张力调节机构中除固定后梁和活动后梁芯轴以外的区域，设定本次优化的效应约束为质量的80%，优化目标依照数模设置为最小质量进行求解，多次迭代后得出拓扑优化的结果如图8所示。从结果可得到可移除、需要保留以及临界区域，整个机构的总重由原来的197.61优化到现在的171.28，减重了13.32%。与静力学分析结果比较后得知移除材料位置均无明显超量的应变与应力，优化较合理。

依据拓扑优化的结果，在SW中进行了相对应的结构优化，具体结构改进包括：固定块长度精简至原来的2/3，宽度过渡面做相应圆角；起桥梁作用的摆臂左侧边角增大圆角至原来的2倍，右下方轮廓向内推进50 mm；作为支承件的轴承座在形状保持不变前提下直径减小10 mm。结构优化后的三维模型如图9所示。

3 仿真验证

3.1 静力学与模态分析验证

将优化后的经纱张力调节机构导入Workbench进行静力学分析，施加与第一节相同的约束和载荷，解算后处理得到机构的总变形云图和等效应力图，结果如图10与图11所示。

静力学分析结果表明（见表2），最大变形由优化前的8.1975×10-4变为2.9293×10-9，最大等效应力由优化前的4.859×106变为1.5664×103，均大幅度变小，且分布更加符合理想的预测效果，验证了结构优化的可行性。

对比优化前后的前六阶固有频率可知（见表3），两者处于同一数量级，机构的动态特性明显提升。综上所述，优化后机构的静态和动态特性均更加符合三维织造对调节机构的响应性要求。

3.2 关键零部件的疲劳分析

经纱张力调节机构需要周期性地运动来调节经纱波动，而调节机构中受载荷最频繁、复杂的就是摆臂。疲劳破坏一般是突发性的，如果没有提前预测会严重影响织造的正常进程，因此对摆臂进行疲劳分析十分关键。下面基于线性累积损伤理论对摆臂进行疲劳分析［22-23］。该理论认为，若零件在循环应力（应力幅σ）作用N次后破坏，那么每次作用对零件产生的破坏是D=1/N，第n次产生的破坏就是D=n/N，现假设零件受循环应力nn次，对应的应力幅σn，此时载荷对零件的破坏可表示为式（5）：

D=1时零件疲劳破坏发生。

摆臂的材料为7075高强度铝合金，在ANSYS中输入材料性能参数并运算，运用Goodman方法修正，获得ε－N曲线。为了得到摆臂载荷情况，在ADAMS中建立了机构多体动力学模型，输入与张力相同规律的激励，仿真得到摆臂处所受作用力，如图12所示。摆臂载荷谱显示，其所受作用力小于1500 N，而设计时所选用气动肌腱作用力范围为0～1600 N，证实了气动肌腱选型的恰当性，故气动肌腱能满足张力调节的需要。

采用nCode搭建摆臂的疲劳寿命分析仿真模型，将摆臂的静力学应力分析结果文件和摆臂材料的ε－N曲线以及载荷谱导入到模型中，求解器设置后进行仿真，后处理得到摆臂的疲劳寿命云图和循环次数与网格节点数对应表，如图13与表4所示。

通过摆臂疲劳寿命云图可知，摆臂在此载荷下最小循环次数为2.824×109，最大循环次数为3.606×1013。比对表4中数据可知最小循环次数对应的单元格为42514，据此判断出循环次数最小点发生在摆臂与活动后梁铰接处，这个最小循环次数换算后为17.91年（假定全年无休，每天12 h工作制），能够满足剑杆织机工作年限需求，契合优化设计目标。

4 实验验证

为了进一步验证拓扑优化对提高三维织机张力调节机构静、动态特性的有效性，在试制的VSI系列三维剑杆织机上进行了对比实验，即分别将制造出的优化前和优化后张力调节机构装配在样机上进行张力采样实验，实况如图14所示。实验在纬密为30根/cm，主轴转速为420 r/min的条件下进行，优化前和优化后经纱张力采样值对比如图15所示。

优化后的张力采样数据最大绝对误差为49.7 kg，比优化前产生的误差少65.7%；相对误差方面，优化后张力控制曲线最大值为4.6%，仅为优化前对应值的49.6%。显然，优化后的织机经纱张力波动更加平稳、调整周期更短、调整速度更快，证明拓扑优化后动态特性明显提升，契合三维织机对张力调节机构的响应性要求。

5 结 论

本文以三维间隔织物织机的经纱张力调节机构为研究对象，为提高其动态补偿特性和响应性，进行了创新设计、拓扑优化和疲劳分析，得到如下结论：

a） 设计了基于气动肌腱的经纱张力调节机构，运用ANSYS对其进行了静力学分析、模态分析，在此分析结果基础上进行了变密度拓扑优化，优化后减重13.32%。

b） 采用仿真实验验证了优化设计的可行性，对优化后的机构进行静力学分析、模态分析并在nCode中采用线性累计损伤理论对机构的关键零件摆臂进行了疲劳分析，仿真结果表明，极限工况下的应力、应变等机械性能保持良好，其静态特性和动态补偿能力得到了显著提升，机构的最小疲劳寿命可达17.91年，满足织机工作年限的需要。

c） 在VSI系列三维织机样机上进行了机构优化前后张力采样值对比实验，进一步证实了拓扑优化设计对提升张力调节机构动态性能的有效性。

d） 完善了经纱张力调节机构设计与优化流程，为采用该方案思路对三维织机其他关键零部件的设计与优化提供了参考。

参考文献：

［1］王斯勇，冯志华，孙浪，等.喷气织机单双后梁系统动态分析与比较［J］.苏州大学学报（工科版），2010，30（1）：56-59.

WANG Siyong， FENG Zhihua， SUN Lang， et al. Dynamic analysis and comparison of the single and double back rest systems for an air-jet loom［J］. Journal of Soochow University （Engineering Science Edition）， 2010， 30（1）： 56-59.

［2］周東波.毛巾织机低惯量后梁响应特性研究［D］.杭州：浙江理工大学，2020：23-34.

ZHOU Dongbo. Research on Response Characteristics of Low Inertia Back Rest of Towel Loom［D］. Hangzhou： Zhejiang Sci-Tech University， 2020： 23-34.

［3］王斯勇.喷气织机双后梁系统设计与经纱张力控制研究［D］.苏州：苏州大学，2010：45-66.

WANG Siyong. Double Back Rests System Design and the Control of Warp Tension on an Air-jet Loom［D］. Suzhou： Soochow University， 2010： 45-66.

［4］武银飞，臧瑞.GA747型剑杆织机送经与卷取机构的配合［J］.上海纺织科技，2017，45（7）：54-56.

WU Yinfei， ZANG Rui. Coordination of let-off and take-up institution on GA747 rapier loom［J］. Shanghai Textile Science & Technology， 2017， 45（7）： 54-56.

［5］郑宝平，蒋高明，夏风林，等.基于模型预测的经编送经动态张力补偿系统设计［J］.纺织学报，2021，42（9）：163-169.

ZHENG Baoping， JIANG Gaoming， XIA Fenglin， et al. Design of dynamic tension compensation system for warp knitting let-off based on model predictions［J］. Journal of Textile Research， 2021， 42（9）： 163-169.

［6］KIM H K， CHUN D H， KIM J H. A study on correlation between warp tension and weaving condition［J］. Fibers and Polymers， 2013， 14（12）： 2185-2190.

［7］黄锦波，祝成炎，张红霞，等.基于剑杆织机改造的三维间隔机织物工艺设计［J］.纺织学报，2021，42（6）：166-170.

HUANG Jinbo， ZHU Chengyan， ZHANG Hongxia， et al. Design of three-dimensional spacer fabrics based on rapier looms［J］. Journal of Textile Research， 2021， 42（6）： 166-170.

［8］陈家新，施广军，杨立新.剑杆织机经纱张力数学模型及仿真［J］.东华大学学报（自然科学版），2012，38（4）：465-470.

CHEN Jiaxin， SHI Guangjun， YANG Lixin. Modelling and simulating of the tension variation in warp yarn on the rapier loom［J］. Journal of Donghua University （Natural Science）， 2012， 38（4）： 465-470.

［9］周其洪.新型高速織机的关键控制技术研究［D］.上海：上海大学，2009：37-39.

ZHOU Qihong. Research on the Key Control Technique of the New Type and High Speed Loom［D］. Shanghai： Shanghai University， 2009： 37-39.

［10］李志鹏.基于双剑杆织机的中空织物织造工艺探讨［J］.纺织科技进展，2019（6）：27-29.

LI Zhipeng. Study on weaving process of hollow sandwich fabric based on double rapier loom［J］. Progress in Textile Science & Technology， 2019 （6）： 27-29.

［11］钟鹏.三维剑杆织机关键技术及结构优化设计［D］.西安：西安工程大学，2017：32-37.

ZHONG Peng. The Key Technology and Optimum Structural Design of Three-dimensional Multi-rapier Loom［D］. Xi'an： Xi'an Polytechnic University， 2017： 32-37.

［12］丁辛.织机后梁动态性能分析［J］.中国纺织大学学报，1993，19（2）：58-62.

DING Xin. An analysis of dynamic performance of back rest of weaving machine［J］. Journal of China Textile University， 1993， 19（2）： 58-62.

［13］刘薇，蒋秀明，杨建成，等.碳纤维多层角联机织装备的集成设计［J］.纺织学报，2016，37（4）：128-136.

LIU Wei， JIANG Xiuming， YANG Jiancheng， et al. Integration design of carbon fiber multi-layer diagonal weaving equipment［J］. Journal of Textile Research， 2016， 37（4）： 128-136.

［14］李鸣超.2.5D机织物的织造工艺设计与下机分析［D］.上海：东华大学，2016：40-46.

LI Mingchao. Weaving Process Design and Analysis Leave the Machine of 2.5D Woven Fabric［D］. Shanghai： Donghua University， 2016： 40-46.

［15］李佳.立体织机经纱系统和打纬机构的设计［D］.上海：东华大学，2013：37-39.

LI Jia. The Design of Warp System and Beating-up Mechanism in 3-D Weaving Machine［D］. Shanghai： Donghua University， 2013： 37-39.

［16］谢枫.立体织机送经系统的设计［D］.上海：东华大学，2014：32-38.

XIE Feng. The Design of Warp System in 3-D Weaving Machine［D］. Shanghai： Donghua University， 2014： 32-38.

［17］金玉珍，胡小冬，林培峰，等.喷气织机打纬机构及墙板的振动特性［J］.纺织学报，2016，37（7）：131-136，141.

JIN Yuzhen， HU Xiaodong， LIN Peifeng， et al. Vibration characteristics of wallboard and four-bar linkage beating-up mechanism of air-jet loom［J］. Journal of Textile Research， 2016， 37（7）： 131-136， 141.

［18］王景良，朱天成，朱龙彪，等.连续体结构的变密度拓扑优化方法研究［J］.工程设计学报，2022，29（3）：279-285.

WANG Jingliang， ZHU Tiancheng， ZHU Longbiao， et al. Research on variable density topology optimization method for continuum structure［J］. Chinese Journal of Engineering Design， 2022， 29（3）： 279-285.

［19］任帅阳，高爱民，张勇，等.六旋翼植保无人机旋翼折叠机构有限元分析及拓扑优化［J］.中国农机化学报，2021，42（9）：53-58，194.

REN Shuaiyang， GAO Aimin， ZHANG Yong， et al. Finite element analysis and topology optimization of folding mechanism of six-rotor plant protection UAV［J］. Journal of Chinese Agricultural Mechanization， 2021， 42（9）： 53-58， 194.

［20］丁飞.爬楼轮椅机架结构有限元分析及其优化设计［D］.天津：河北工业大学，2016：43-47.

DING Fei. The Finite Element Analysis and Optimization Design of a Stair-climbing Wheelchair Frame［D］. Tianjin： Hebei University of Technology， 2016： 43-47.

［21］WANG H， CHENG W M， DU R， et al. Improved proportional topology optimization algorithm for solving minimum compliance problem［J］. Structural and Multidisciplinary Optimization， 2020， 62（2）： 475-493.

［22］劉俊，张海剑，王威，等.基于轮胎六分力的某商用车车架疲劳分析［J］.中国机械工程，2019，30（21）：2583-2589.

LIU Jun， ZHANG Haijian， WANG Wei， et al. Fatigue analysis of commercial vehicle frames based on Six-dimensional wheel loads［J］. China Mechanical Engineering， 2019， 30（21）： 2583-2589.

［23］陈鹏.基于主动学习神经网络的转向架构架疲劳可靠性分析［J］.计算力学学报，2022，1（3）：1-9.

CHEN Peng. Fatigue reliability analysis of bogie frame based on active learning neural network［J］. Chinese Journal of Computational Mechanics， 2022， 1（3）： 1-9.

Abstract： The main function of the warp feeding system of a three-dimensional weaving machine is to feed the yarn required for weaving according to the weft density requirements of the fabric structure and to keep the warp tension stable during the weaving process by using its own regulating movements. The three-dimensional weaving machine has two ground warps for weaving ply yarns and a pile warp for "standing" of the fabric， which are coupled to form the warp feeding system of the entire interval fabric weaving machine. Each warp feeding system consists of three parts， namely， the warp feeding shaft parts， the warp tension regulator and the tension detection device. The warp tension regulator is the key part of the warp feeding system for dynamic compensation and is the core of the warp feeding function. With the development of high-speed and intelligent weaving machines， the dynamic compensation capability of the warp feeding system has become more demanding for interval fabric weaving machines.

In order to improve the dynamic compensation capability of the warp tension adjustment mechanism and to adapt to the high-speed weaving needs of the three-dimensional spacer fabric rapier weaving machine， a new warp tension adjustment mechanism is designed from the functional principle by introducing a variable stiffness pneumatic tendon as the prime mover that can absorb stress. The static stress and strain characteristics as well as the first six orders of inherent frequency pattern were obtained by using finite element technique. On this basis， the improved variable density method was used to optimize the topology of the mechanism， and then the structure was optimized in Solidworks according to the optimization results， and the finite element simulation experiment was used to verify the static and modal characteristics of the optimized mechanism. The fatigue life prediction based on linear cumulative damage theory was then performed on the core part of the mechanism， the swing arm， to confirm whether it meets the weaving needs after optimization. The results show that the topologically optimized mechanism has a weight reduction of 13.32%， while the static and dynamic properties such as stress， strain and inherent frequency are greatly improved， and its minimum fatigue life can reach 17.91 years， which meets the needs of the service life of the three-dimensional loom. Finally， a comparative experiment was conducted on a VSI series prototype to analyze the tension sampling curves corresponding to the optimized warp tension adjustment mechanism before and after the optimization. The experimental results show that the warp tension fluctuation in the optimized weaving machine is smoother and more accurate， and the dynamic characteristics of the mechanism are effectively improved.

The perfect design and optimization process of the warp tension adjustment mechanism can help to promote the improvement of the weaving quality of the three-dimensional loom， and the corresponding design optimization and experimental verification of other key components of the three-dimensional loom can be carried out according to the idea of this scheme， in order to meet the development requirements of high-speed and intelligent three-dimensional loom for spacer fabrics. At the same time， knowledge of dynamics can be introduced to study the various influencing factors in the weaving motion of the mechanism and to promote the joint improvement of the warp feeding system and other systems in the weaving machine.

Keywords： tension regulating mechanism; topology optimization; lightweight design; modal analysis; fatigue life analysis; spacer fabric three-dimensional loom