基于小波收缩的改进阈值脑电信号去噪方法研究

楚瑞博，王 剑，2，张 迁，陈欢欢

（1.昆明理工大学 信息工程与自动化学院，云南 昆明 650504；2.昆明理工大学 云南省人工智能重点实验室，云南 昆明 650504）

0 引 言

脑电（EEG）信号是一种记录大脑皮层产生的电活动的无创方法[1]，由于其成本低、时间分辨率好，常被用于癫痫等疾病的诊断。近年来，由于脑机接口技术的发展，脑电信号也被广泛应用于睡眠监测、情绪识别和神经系统研究等领域[2]。

脑电信号是一种随机性很强的非线性非平稳信号[3]，在原始脑电信号的采集过程中，由于眨眼、眼球运动、肌肉活动和电子设备信号的干扰，导致采集的脑电数据存在较大误差，这对信号的分析和研究工作产生了很大的影响[4]。因此，脑电去噪在脑电研究中起着十分重要的作用，降噪效果的优劣将直接影响到脑电信号的特征提取和识别。

小波变换在图像处理、信号处理等方面得到了广泛的应用。小波去噪技术包括模型极大值法、空间滤波法、阈值法等，而阈值法目前是国内外学者研究较多的一种去噪方法[5-6]。选取合适的阈值函数是小波阈值去噪的关键问题，其对脑电信号去噪的质量效果也会产生直接影响。作为最常用的两种传统阈值函数，无论是软阈值函数还是硬阈值函数在小波阈值中都发挥着重要作用。使用硬阈值函数对脑电信号去噪可以较好地保留脑电信号边缘细节等局部特征，但是处理后的脑电信号连续性较差；使用软阈值函数处理脑电信号虽然比硬阈值函数要更加平滑，但是会造成脑电信号一些奇异点的消失，并损失大量细节信息[7-8]。随着小波降噪技术的进一步发展，各种在软硬阈值函数的基础上而改进的阈值函数算法被陆续提出。文献[9]提出一种自适应阈值函数算法，利用小波变换对脑电信号进行分解得出小波系数，并以此为基础进行阈值处理，去除噪声信号，从而达到去噪的目的。相对于软阈值函数，此种方法较好地保留了原始信号的特征，进一步提高了信号去噪效果。文献[10]针对癫痫脑电数据提出了一种以拉普拉斯为最大后验概率估计，并通过小波变换处理脑电信号，以此得到小波变换处理后的小波系数，采用贝叶斯算法进行预估小波变换后的小波系数，然后对脑电信号进行重构，进而完成对脑电信号的去噪。文献[11]将小波去噪法和最小均方误差（MMSE）相结合，设计了一种自适应的阈值选取器，提出了一种基于自适应阈值的LMS 算法，通过提升格式的小波变换算法进行仿真信号的去噪实验，该方法能有效地减少噪声，提高信噪比，比传统的去噪方法去噪效果更精确。随后Donoho 和Johnstone 提出了小波收缩去噪理论，这种算法充分利用了正交小波基的特性，并结合正交小波的特性和信号与噪声的不同性质，可以有效地消除干扰。

本文提出的新阈值法是基于小波收缩的改进阈值法，并对脑电信号进行了去噪实验。实验结果表明：本文提出的基于小波收缩的改进阈值方法对脑电信号的去噪效果相对于软硬阈值方法和自适应阈值方法要更好、信噪比（SNR）更高、均方根误差（RMSE）更低。

1 小波阈值去噪

1.1 小波阈值去噪原理

将脑电信号通过小波变换（采用Mallat 算法）分解后成功得到已经处理好的脑电信号，产生的小波系数具有明显的特征，其包含脑电信号的基本信息，分解后噪声的小波系数要小于脑电信号的小波系数，设定相应的阈值，大于此阈值的小波系数被认为是由脑电信号产生的，对其保留；小于此阈值的高频小波系数则为噪声产生的，将其去除。然后重构处理后的低频系数和高频系数，从而完成脑电信号的噪声去除。

1.2 小波基函数的选择

选择合适的小波基函数可以使脑电信号的去噪效果更优，具有良好对称特性的小波基函数在对脑电信号处理时不会发生相位畸变。在进行脑电信号重构时，选择具有良好正交性的小波基能使重构后的脑电信号更加平滑，选择紧支撑的小波基函数可以加快脑电信号去噪时的处理速度。

1.3 阈值函数的选择

在对小波阈值去噪这一过程中需要重点关注阈值函数的选取，合适的函数直接影响去噪效果。通常情况下，去噪时采用的传统阈值函数有两种，即硬阈值函数[12]和 软 阈 值 函 数[13]。

2 改进阈值方法

虽然正交小波在一定程度上可以降低噪声，但是为了拥有更好的去噪效果，可根据每一个尺度下噪声的水平对其设置不同的阈值，也就是多尺度小波阈值降噪，又称为小波收缩（Wavelet Shrinkage）。硬阈值函数是一种简单的归零方法，并且硬阈值函数不具有良好的连续性，其重构后信号会产生震荡；软阈值函数是将绝对值较大的系数降低到一定程度，然后重构处理后的小波系数，但是经过软阈值函数重构后的信号会存在较大畸变。因此，本文提出了自适应小波收缩阈值函数，其表达式如下：

由式（1）可得，在|wj,k|=T时，，证明引入的自适应小波收缩阈值函数连续，并且在|wj,k|→∞时：

在|wj,k|→-∞时：

式中：参数k是分解层数；N为信号的长度；σ为噪声的标准误差。本文改进的阈值随着分解尺度的变化而变化，并且减少了计算量。改进后的阈值Tk与分解层数呈现出反比关系，符合噪声的特点，在不受人工干预的条件下能根据不同情况自动调节，从而达到了自适应特性。

3 实验结果及分析

3.1 实验数据采集

本次实验采用格茨数据集2a（Data sets 2a），该数据集由9 名不同的受试者脑电信号组成，实验数据的采样频率为250 Hz。BCI 范例分别给予了4 种不同的运动想象任务，分别是：左手、右手、双脚和舌头的四种类别的运动想象，分别从22 个Ag/AgCl 电极记录EEG 信号。按照国际标准10-20 系统，放置脑电信号的电极，所有脑电信号均以左侧乳突为参考电极，右侧乳突为地面电极记录。本实验选取受试者的测试数据集中Fz 通道的EEG 进行去噪实验，截取前10 000 个采样点进行分析。

3.2 实验结果及分析

本实验使用Matlab 2020a 平台对脑电信号进行去噪处理。为了便于判定各种阈值函数的性能优劣，实验中的评价指标为信噪比（SNR）与均方根误差（RMSE），其定义分别为：

式中：N为脑电信号的长度；f(i)是原始脑电信号；͂(i)是去噪重构后的脑电信号。脑电信号进行去噪后的信噪比（SNR）越高、均方根误差（RMSE）越低，则表明脑电信号进行去噪实验的效果越好[14-15]。

经过实验测试了haar 小波、sym6 小波、coif5 小波、db6 小波的去噪效果，本文选择的小波基函数为db6 小波，db6 小波曲线如图1 所示。

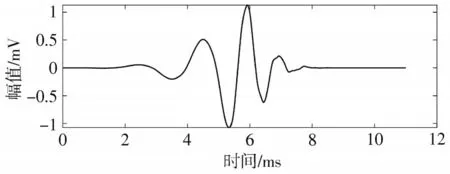
图1 db6 小波函数

经过测试本文选择的分解层次为5 层。图2 是Fz通道原始脑电信号采样点的波形图，图3 是Fz 通道原始脑电信号采样点经过小波分解5 层后低频部分的小波系数a1，图4 是Fz 通道原始脑电信号采样点经过小波分解5 层后高频部分的小波系数dn，图5 是Fz 通道原始脑电信号采样点经过小波分解6 层后低频部分的小波系数a1，图6 为Fz 通道原始脑电信号采样点经过小波分解6 层后高频部分的小波系数dn。从图中可以看出当分解层数低于5 层时，由于分解层数过低从而导致噪声不能去除完全，所以细节系数的波形图与原始脑电信号的波形图差别较大，当分解层数为6 层时，其细节系数的波形图边缘细节部分失真较大，并且加大了处理时的计算量。因此本实验选择了分解层次为5 层，因为原始脑电信号的波形与图4 中的小波分解5 层后的波形图相似度更高，所以选择分解层次为5 层。

图2 原始脑电信号

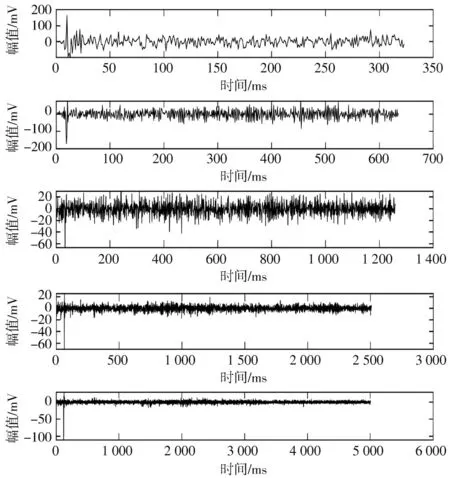
图4 脑电信号进行5 层小波分解细节系数dn

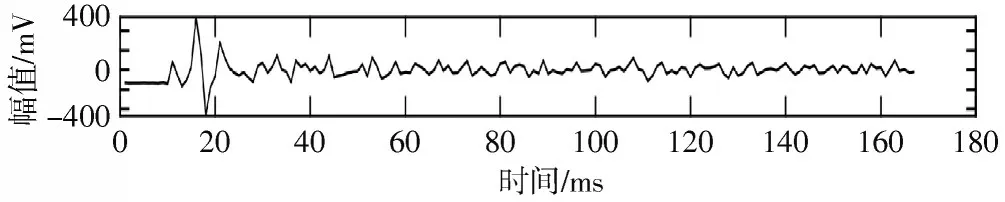
图5 脑电信号进行6 层小波分解近似系数a1

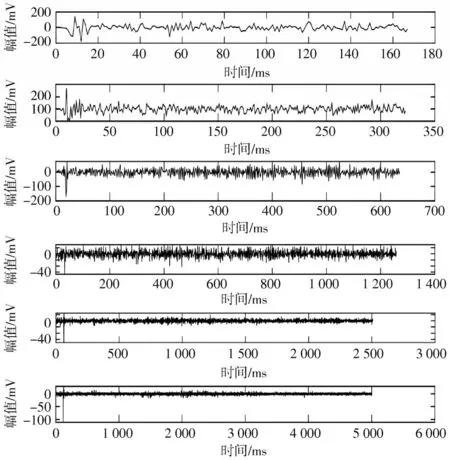
图6 脑电信号进行6 层小波分解细节系数dn

图7 为原始脑电信号采用db6 小波基使用硬阈值、软阈值、自适应阈值和本文改进的阈值算法去噪后的效果图。从图7 中可以看出：实验一采用硬阈值算法去噪，虽然保留了脑电信号的边缘细节信息，但是脑电信号的连续性较差，重构的脑电信号有震荡，不能很好地保留原始脑电信号的特征；实验二采用软阈值算法去噪，脑电信号的一些奇异点被淹没，造成大量脑电信号细节信息的丢失，其重构的脑电信号有较大的失真；实验三采用自适应阈值去噪，相对于两种传统的阈值去噪方法，该方法有计算量低、运算速度快等特点，能有效地保留脑电信号的细节信息，脑电信号较为平滑，但是该方法去噪后的脑电信号高频部分毛刺较多；实验四采用小波收缩改进阈值算法对脑电信号去噪，通过效果图对比可以看出，去噪后的脑电信号波形图与原始脑电信号波形图相似程度较高，不但保留了脑电信号的高频部分和低频部分的细节信息，而且重构后的脑电信号高频部分的毛刺相对于自适应阈值去噪方法减少，脑电信号也变得更加平滑，同时重构后的脑电信号与原始脑电信号的变化趋势相吻合。

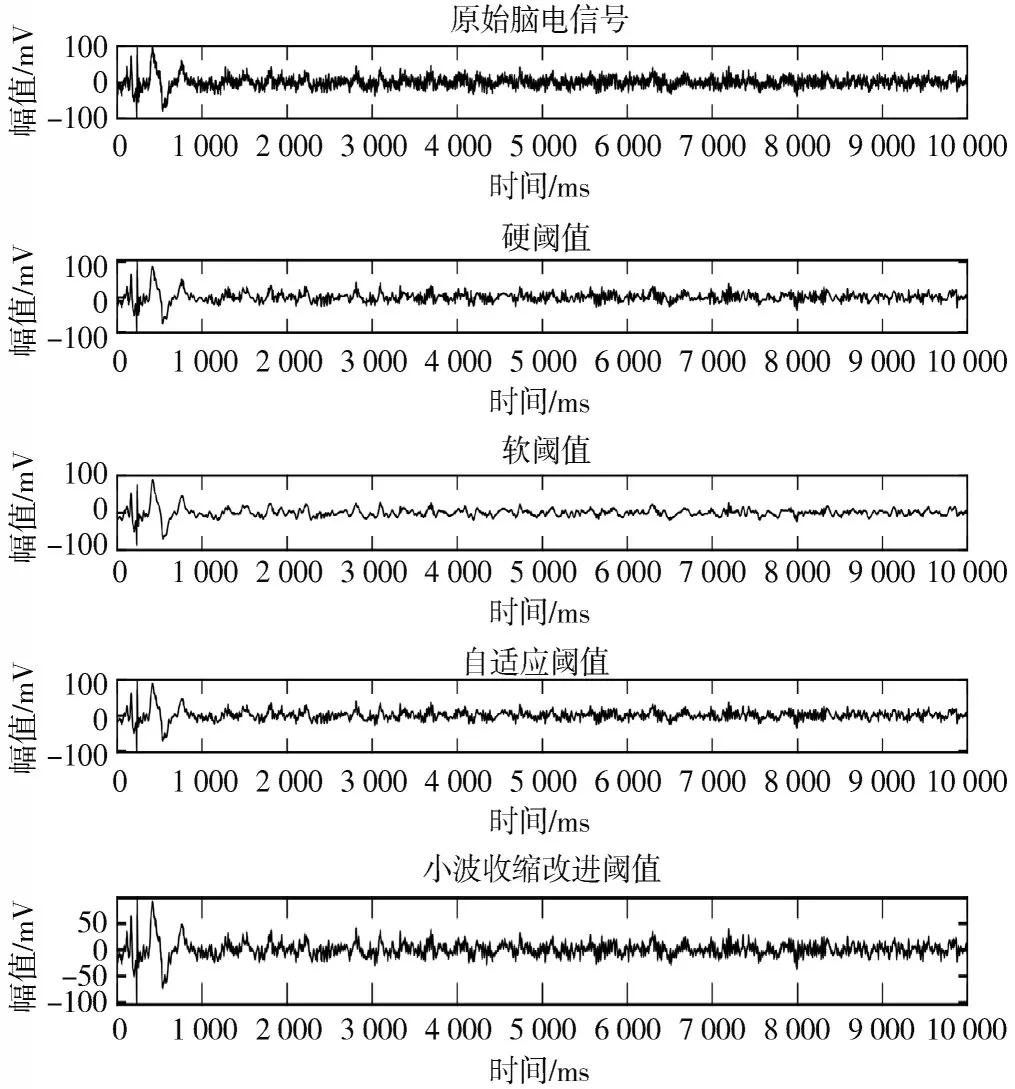
图7 脑电信号去噪效果图

本文将采用不同的阈值算法进行脑电信号去噪实验，并将对比采用db6 小波、sym6 小波、coif5 小波、haar小波4 种不同的小波基函数所得到的SNR 和RMSE 的结果，如表1 所示。

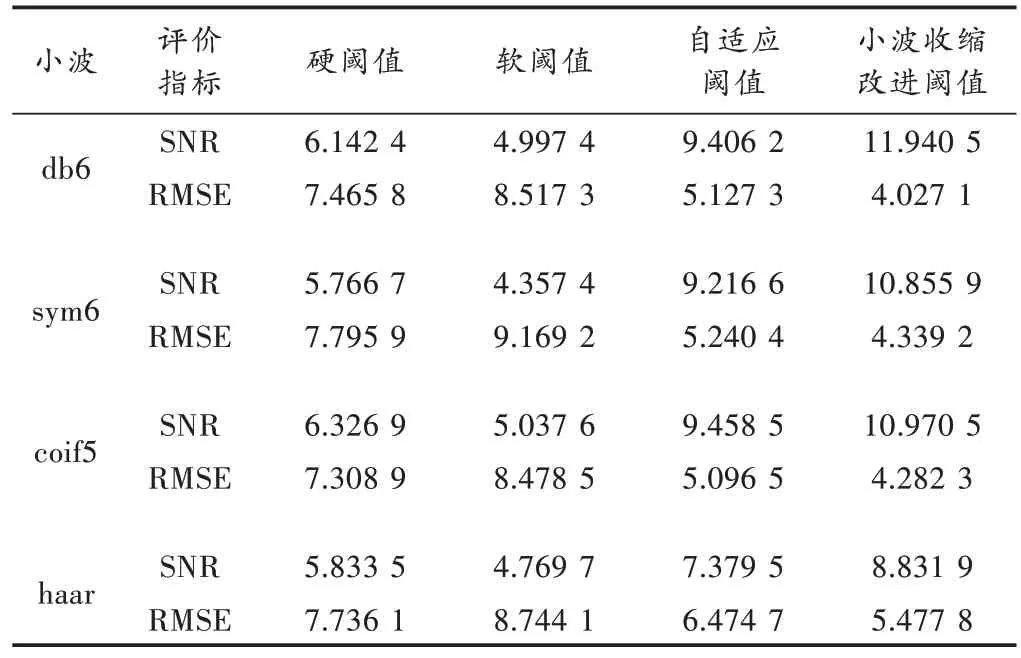
表1 不同阈值算法去噪效果的数据结果

从表1 中的数据可以看出：改进的阈值算法在采用不同的小波基函数对比其他阈值算法SNR 的值最高，同时其RMSE 的值最低，即去噪后脑电信号中有效成分与噪声成分的比值最大；去噪后信号与原信号之间的偏差最小，具有明显优势，去噪效果较好，并且在采用db6小波时其效果最好，从而得出使用本文改进的阈值算法相比软硬阈值算法以及自适应阈值算法对脑电信号的去噪效果更优。

4 结 论

本文将小波收缩和阈值法结合提出一种基于小波收缩的改进阈值去噪方法，并将其运用于脑电信号中噪声信号去除。选用db6 作为小波基函数，对含噪的脑电信号分别使用了硬阈值法、软阈值法、自适应阈值法以及本文提出基于小波收缩的改进阈值法进行实验，以脑电信号去噪后的效果图和SNR、RMSE 等指标评判去噪效果。实验结果表明，改进的阈值去噪算法对脑电信号的去噪效果要优于两种传统阈值去噪算法和常用的自适应阈值去噪算法，不仅有效地抑制了高斯噪声，又比较好地保留了原始脑电信号中的基本波形特征。本文的脑电信号去噪方法需要进一步完善，小波变换处理脑电信号时需要手动选择小波基，因此在后续工作中，可对如何自适应选取小波基作进一步研究。

注：本文通讯作者为王剑。