一种近空间飞行器整数规划复合控制分配方法 *

潘彦鹏，李迎博，张雪婷，谭黎立

（中国运载火箭技术研究院，北京 100076）

0 引言

近空间飞行器的飞行空域跨越稀薄大气层和稠密大气层，具有空域广、动态高等显著特点。由于其飞行环境特殊，依靠单一的气动控制难以满足飞控任务需求，通常采用复合控制方式，如RCS（reaction control system）+气动舵复合［1］、推力矢量+气动舵复合［2］、质量矩控制+气动舵复合等，由此产生了一个新的控制问题——异构复合控制问题［3-5］。如何对2 种控制特性显著不同的控制力矩进行分配，以最大限度地提升控制效能，是异构复合控制的难点问题。

RCS+气动力复合是目前近空间飞行器上应用最广泛的复合控制方式，国内外已有大量研究资料，对此类异构复合系统的控制律及其优化算法进行了研究［6-11］。主要解决思路是按照连续力矩执行机构产生的控制力矩需求进行分配，在分配方法方面采用线性或非线性的逐步过渡式分配，实现从RCS 力矩到控制力矩的控制过渡。但其方法仍有不足，主要体现在：①没有考虑异构特性带来的连续/离散混合动态系统特性，仍然按连续系统来设计；②控制分配中没有考虑执行机构异构的差异性，导致实际分配效果难以达到期望效果，姿态震荡和RCS 能量消耗都较大。本文以近空间飞行器为研究，针对上述问题②的技术难点，提出了一种基于整数规划策略的控制分配方案。该方法将直/气复合控制分配的力矩实现问题转为一个0-1 整数规划问题，使规划出的分配指令更加接近RCS 开关特性下的力矩实现，更有利于提升控制平稳性和降低能量消耗。

1 姿态运动模型

近空间飞行器常为升力体BTT（bank-to-turn）飞行器，姿态模型如下：

式中：v为速度；ωx，ωy，ωz为角速度；I1～I10为转动惯量决定的常数；α，β，μ分别为攻角、侧滑角和速度倾斜角；Y，Z分别为升力和侧向力；Mx，My，Mz为合外力矩，可表示为

式中：M0为除气动舵控制力矩之外的其他气动力矩；MRCS为RCS控制力矩；Mfin为气动舵产生的控制力矩。

2 控制分配问题的整数规划方法描述

本文的控制分配问题可描述为：如何实时调整RCS 和气动舵参与控制的比例，也即MRCS和Mfin的作用比例，使系统以某个最优指标达到期望的控制效果。

控制分配策略不仅要完成异构执行机构间控制作用分配，还要满足从RCS 控制到气动舵控制的平滑切换过程。由于气动控制严重依赖于动压，因此采用如下的基于动压包络线的分配函数：

式中：Mand为需求控制力矩，分别为分配至RCS 和舵面的需求力矩；kx为权重系数，复合控制段的动压通常单调递增，因此kx一般取为

式中：qdyn1和qdyn2为复合控制开始阶段和结束阶段的动压值。

从连续控制系统的角度来讲，式（4）可以实现2种执行机构控制作用的平缓过渡，但由于RCS 的离散输出特性，将存在下列问题：

（1） 难以实现从RCS 到气动舵控制的平缓过渡；

（2） 容易引起舵面的频繁震荡，造成燃料的额外消耗；

（3） 姿态的平稳性通常难以满足要求。

为此，采用基于整数规划的策略，使RCS 系统的实际输出力矩尽可能地逼近分配的指令力矩，以达到在保证姿态过渡过程要求的同时实现异构执行机构控制作用间的平缓过渡。

假设推力器输出为Ft，配置个数为n，则式（3）中RCS 合力矩可表示为

式中：At为RCS 配置矩阵；ai为推力器i的配置向量；x为n个推力器组的开关机指令向量；Ft为推力，则任意时刻的推进剂消耗量与式（7）成正比关系：

式中：Ftmax为推力器输出的最大推力。

因此，基于整数规划策略的控制分配实现问题可描述如下的最优解求解问题。

求解满足：

的一个最优解x，其中：cij为权重因子；bi为i通道的RCS 力矩指令。

3 整数规划算法设计

本文控制分配的实现过程也即求解式（8）描述的整数规划（integer programming，IP）问题［12-17］。为简化求解过程，先求解对应的松弛问题，即略去整数约束条件，将其视为一个单纯的线性规划问题（linear programming，LP）进行求解，然后对其最优解进行取整处理。由于RCS 系统是一个强离散输出特性的控制对象，取整处理得到的解未必是式（8）的最优解，甚至可能连可行解都不是。这里借鉴松弛问题及可行解区域分解优化的处理思想，采用分枝定界法来处理式（8）描述的IP 极值问题。

记式（8）描述的IP 问题为P，与之对应的松弛问题为P0，则问题P0的解与原问题P的解满足如下的基本关系：

（1） 若问题P0没有可行解，则问题P也没有可行解；

（2） 若问题P0有最优解，并符合问题P的整数条件，则该最优解也是P的最优解。

基于P与P0解的基本关系和分枝定界法基本操作，问题P的分枝定界法求解步骤如下：

（1） 初始步，求解P问题的松弛问题P0

1）P0问题的解判定：若P0没有可行解，则P也没有可行解，停机；若P0有可行解，则转2）。

2） 判定步骤1）解是否符合问题P的整数条件？若是，问题P0的解即为问题P的最优解，则寻优成功，停机；若为否，则转3）。

（2） 迭代步

1） 记P0问题的目标函数值为P问题的最优目标函数z*的上界，任意选取问题P的一个整数可行解（如xj= 0），求其目标函数，显然，有成立。

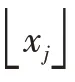
3） 比较和定界：找出各分枝（子问题）的最优值，有小于下界值的，则丢弃这个分枝；若大于，且不符合整数条件，则返回4），直到得到为止。

分枝定界法的计算流程如图1 所示。

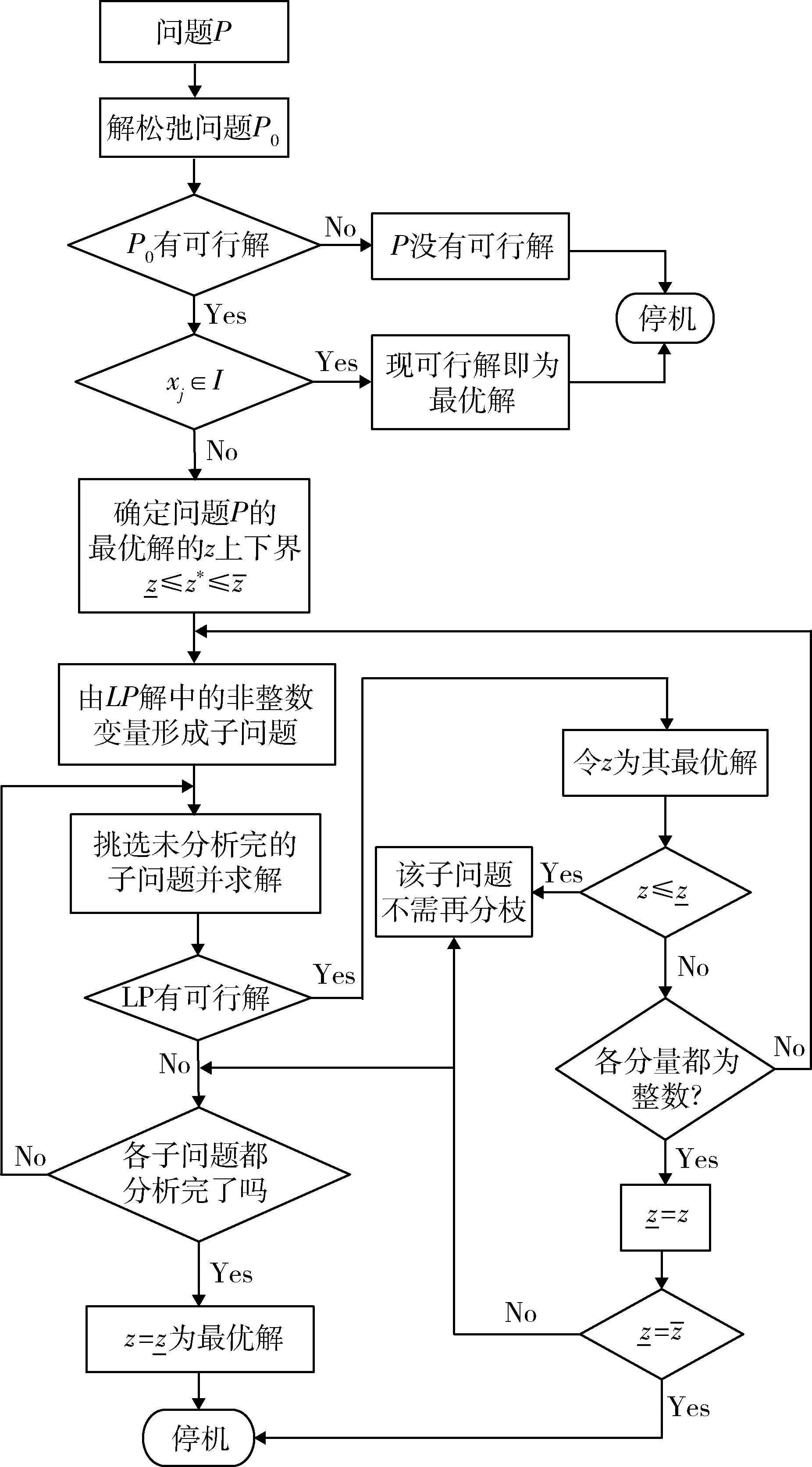
图1 IP 极值问题的分支定界算法流程Fig. 1 Flow of branch and bound method for IP extremum problem

4 仿真校验

某近空间飞行器的RCS 系统采用如图2 所示的配置方案。

图2 RCS 配 置 示 意 图Fig. 2 RCS configuration

其配置矩阵为

式中：推力器采用梯形模型，额定推力为160 N，上升/下降时延2 ms，复合控制开始高度H=80 km，对应动压qdyn1= 300 Pa，结束高度H=60 km，对应动压qdyn1= 3000 Pa，开机指令向量上界初值选= 1，下界初值选= 0，权重因子cij均取值为1。采用本文控制分配算法得到的仿真结果如图3，4 所示。

图3 优化前后3 通道总冲消耗对比曲线Fig. 3 Comparison of total impulse consumption of three channels before and after optimiza tion

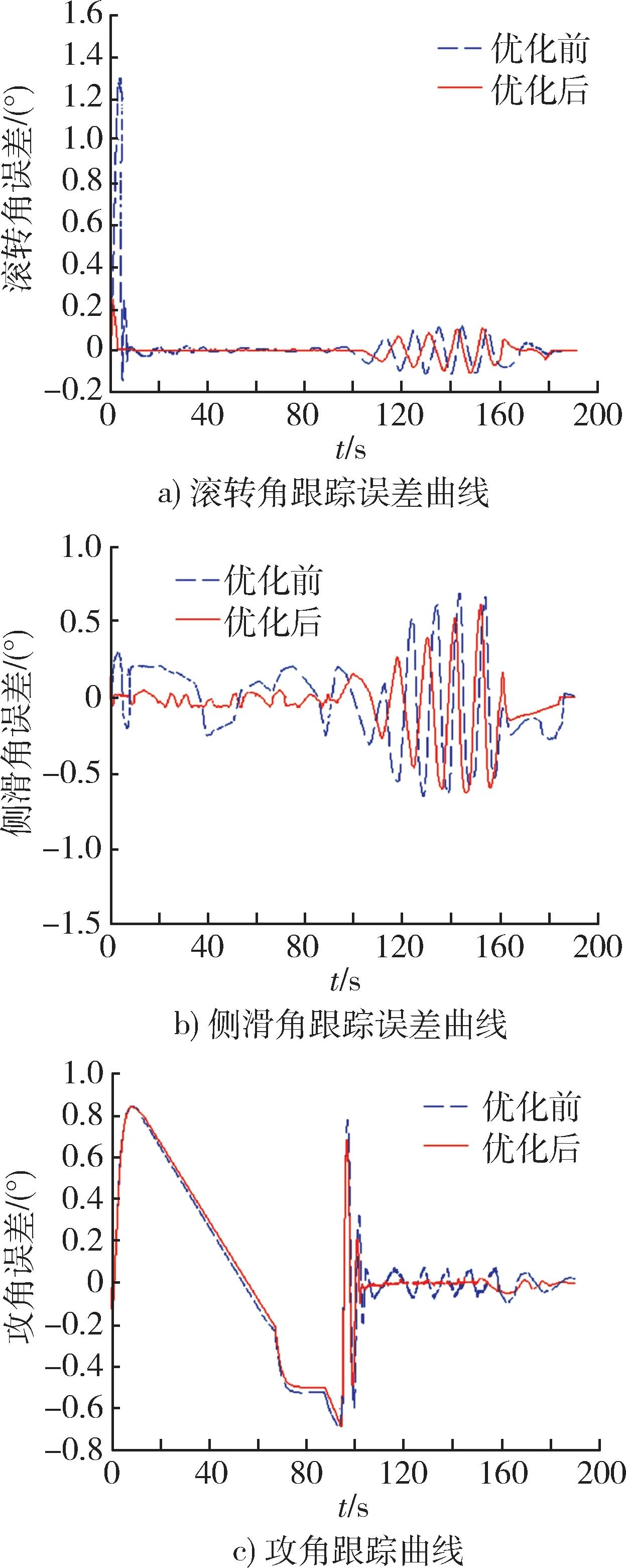
图4 优化前后三通道姿态角跟踪误差曲线Fig. 4 Comparison of attitude angle-tracking error of three channels before and after optimization

通过对比分析图3，4 的优化前后总冲与跟踪误差，可以看到，采用整数规划分配控制后，各通道的总冲消耗总量和姿态角跟踪误差均有明显减小，说明本文方法能有效减少复合控制阶段的姿态震荡以及由此引起的额外控制能量消耗，有利于降低RCS 系统的控制能量消耗总量。

5 结束语

本文针对近空间飞行器的异构复合控制问题，提出了一种基于整数规划策略的控制分配方法，以解决异构执行机构特性差异导致的姿态震荡和RCS能量消耗较大的技术问题。仿真结果表明，本文提出的方法能有效降低RCS+气动舵复合系统的能量消耗总量和姿态震荡。