基于改进连通区域标记的跳频信号分选识别 *

郭昭艺，黄祥，孟悦，杜彪，霍丹江

（江苏方天电力技术有限公司，江苏 南京 211102）

0 引言

近年来，由于中国低空空域的逐步打开，无人驾驶飞行器也逐步地由军事领域延伸至民用领域［1］，但在提供方便的同时，却也造成了“黑飞”“滥飞”等事故时有发生，这将会对电力设施等设备的安全平稳运营造成很大的安全威胁［2-3］。所以，很有必要进行中低空领域反无人机攻击的关键技术研发。

反无人机入侵技术的关键是对无人机信号开展侦察识别。为了增加传输的稳定性，小型商用和民用无人机通常采用ISM（industrial scientific medical band）频段的跳频信号作为遥控指令来进行飞行控制。该频段中包含的通信信号复杂而拥挤，会形成较多的噪声和干扰，如何实现复杂电磁环境下跳频信号的分选识别，进而实现对“黑飞”无人机的检测，成为反制无人机亟待解决的重难点问题。

当前，一些研究者已经对跳频信息的测量和分选识别等问题开展了研究。Chung C. D. 等在掌握信号先验知识条件下对跳频信号局部参量作出了估算［4-5］，不能达到通信对抗的需求。针对非平稳的跳频信号，大多数采用时频分析技术来实现参数盲估计。Barbarossa S. 等采用不同的时频分析技术获取相关的峰值曲线来实现参考估算［6-7］，但是该技术需要比较高的信噪比。为此，一些学者给出了一个采用时频脊线的跳频时间信息参数估算方案［8-9］，可以在较低峰值信噪比条件下实现参考估算。但是，这些方案均针对接收信道中仅存在一条跳频信息的特殊情形，而在出现定频、突发等其他干扰情况时方式均无效。一些学者也从图像处理的角度研究跳频信号检测识别问题［10-13］。文献［10］对时频图像不同尺寸的结构元素完成形态学处理，从而消除了干扰，但该方法必须选定结构元素的尺寸。文献［11］使用了一种二维模板匹配的方式进行指定跳频信号的检测识别，但虚警率较高。文献［12-13］中将信号时频矩阵转换为灰度时频图像，经阈值化后采用形态学滤波消除定频干扰等影响，从而完成了跳频信号参数估计。以上方式都需要经过人工干预设置合适的门限，仅能估计跳频信号部分参数，在复杂干扰环境下的检测识别效果不佳。

本文采用时频图像连通区域聚类方法解决复杂电磁环境下混合信号中的跳频问题。首先，采用基于能量统计的自适应阈值噪声去除方法去除信号时频 图中的背景噪声；然后，通过连通区域标记将信号区域聚集，接着对各区域进行参数提取、聚类和统计，从而实现了复杂电磁环境下跳频信号的分选。

1 时频信号的预处理

1.1 跳频信号时频分析

跳频信号的频点是随着时间而不断变化的，因此可采取时频分析的方法来描述信号在频域中的变化特征。本文采用短时傅里叶变换法，该方法不会产生交叉特征干扰，且计算工作量也较小。

对于跳频信号，接收端和发送端信号的关系可表示为

式中：x(t)为无人机发射的跳频信号；s(t)为侦察设备接收到的信号；n(t)为噪声。

对接收信号s(t)进行短时傅里叶变换，可表示为

式中：h(t)为时间长度很短的窗函数，这里取矩形窗。经过短时傅里叶转换，将接收信息s(t)转换成时间-频率二维函数，从而形成二维时频图。

1.2 基于局部窗口能量门限统计的去噪

ISM 频段是一种开放的频段，接收信号中除了无人机跳频遥控信号外，还混有大量的噪声和干扰（定频干扰和斜变信号干扰）。

对接收信号进行短时傅里叶转换，可以分别获得如图1 和图2 所给出的在无噪声和有噪声条件下的信号时频分布图。可以看到，噪声对目标信号的时频图影响较大，会影响后续的信号参数估计和信号分选，需要进行降噪处理。

文献［14］采用基于能量统计的自适应门限去噪方法，该方法用整个时频分布能量进行统计来估计能量门限，适用于噪声均匀分布的情况。由于噪声在不同时间和频段存在不同分布，因此可采用基于局部窗口能量门限统计的自适应去噪方法。

根据噪声强度将信号二维时频能量分布划分为K个区域，设第i个区域的时频能量分布矩阵为Ti(x，y)，则局部区域时频能量分布矩阵的平均能量为

式中：Mi和Ni分别表示局部区域i的频域点个数和时域点个数。不同区域的去噪门限可表示为

式中：ai为区域i的去噪系数，表示该区域的平均能量的倍数。去噪后的二维时频分布可表示为

式中：K为局部区域数。在信号二维时频能量分布中，由于噪声能量小于目标时频点能量，且数量远大于目标信号时频点，因此可以通过遍历统计法计算合适的去噪门限，具体步骤如下：

步骤1： 在不同区域中分别对去噪系数ai从0到10 等间隔取值，取值间隔为0.1，然后根据式（4）得到不同区域下的去噪门限thi(k)。

步骤2： 统计不同门限下能量大于阈值点的数目c(k)，可表示如下

步 骤3： 找 出c(k)，k= 1，2，…，Nk下 降 最 大 处的点，即c(k+ 1)较c(k)有最大的下降，则c(k+ 1)对应的thi(k+ 1)为最终的去噪门限thi。

步骤4： 按式（5）计算，得到去噪后的时频分布，即Fi(x，y)。

2 基于连通区域标记的参数提取

2.1 连通区域标记

去噪后的时频分布仍然混杂着定频、斜变等干扰信号。从时频分布中可以发现，信号分布呈现规则区域的连通特性，每个连通区域的属性可以很好地表征信号的参数特性，对不同连通区域进行聚类则可以实现信号的分选。

本文采用基于区域生长思想的8 邻域连通方法，常见的8 邻域连通如图3 所示。

图3 8 邻 域 连 通 图Fig. 3 Eight neighborhood connectivity

文献［15］中使用了二值化的时频矩阵作为连通算法的输入，该方式会损失信号的幅度信息，尤其当多目标信号混叠时，并不能充分利用幅度的变化信息。因此，本文中使用了含有一定幅度原始信息的时频矩阵F作为输入矩阵，并构建连通标记矩阵B，其大小与F相同，构建队列queue矩阵并初始化，初始化标记计数label_count=0。

算法实现流程如下：

输入：去噪后的时频矩阵F(x，y)，x和y分别为时间轴（横坐标）和频率轴（纵坐标）上的坐标。

输出：标记矩阵B(x，y)。

步骤1： 先依次扫描A，当扫描到非零点p且未被标记时，即label_count=label_count+1 时，在B上将label_count的数值赋于p位置，同时扫描p的邻域点，如果出现了未被标记的非零点则在B中加以标注，并置于queue中，以作为区域内生长的种子。

步骤2： 若queue不为空时，从queue中取出点p1，扫描p1的8 邻域点，若存在未被标记的非零点，则在B中进行标记将lobel_count的值赋予该点，并放入queue中。

步骤3： 如果queue为非空矩阵，在queue中提取点p1，并扫描p1的邻域点，如果出现了未被标记的非零点，则在B中进行标记后将lobel_count的值赋于该点，并存放在队列queue矩阵中。

步骤4： 当queue为空时，一个连通区域标记完成。

步骤5： 直至整个矩阵扫描完毕，则得到标记矩阵B。

连通标记处理后，2 类矩阵示意图如表1 所示。

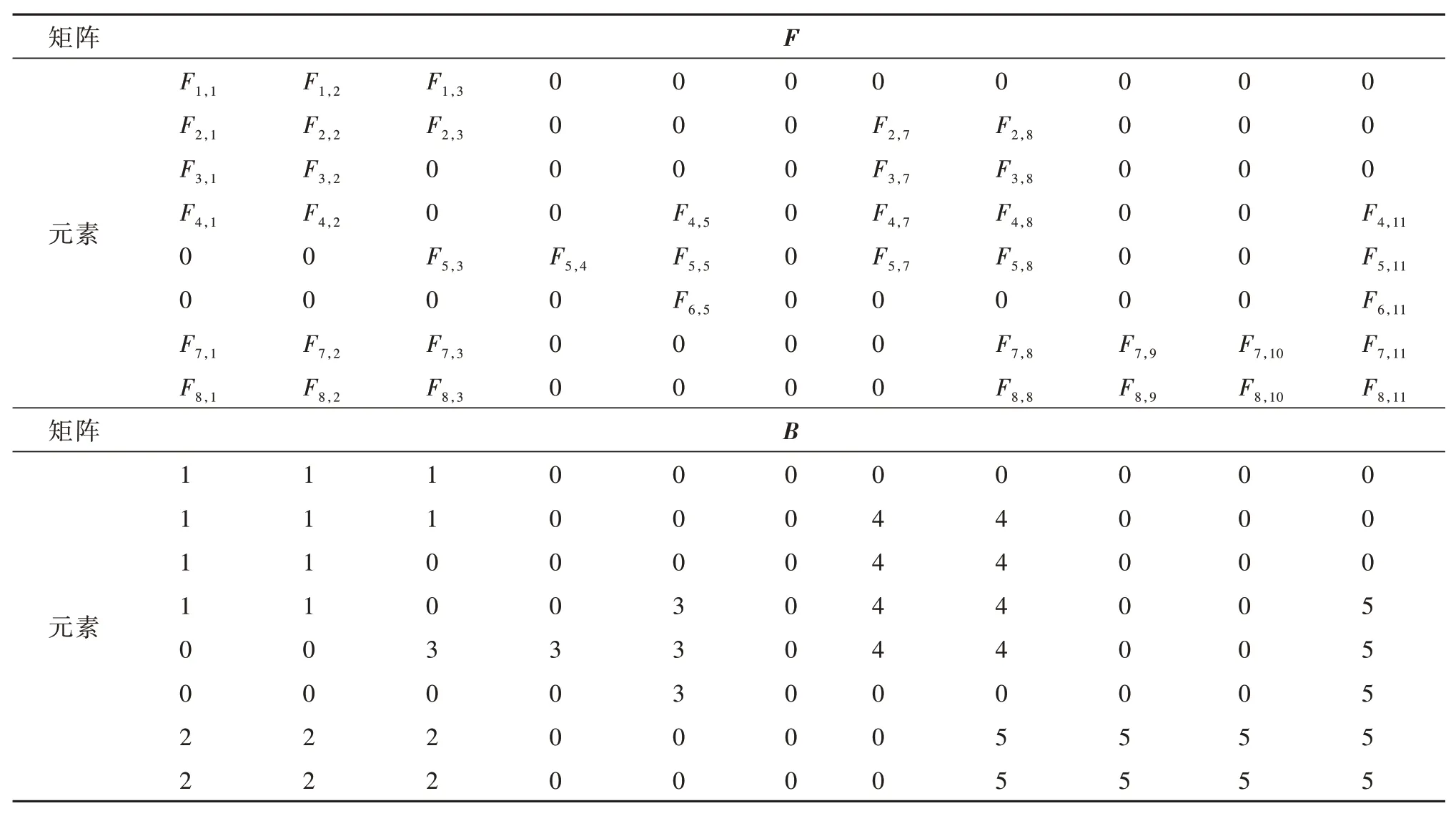
表1 时频矩阵F 和标记矩阵B 示意图Table 1 Time-frequency matrix F and label matrix B

2.2 时频参数提取

在对信号时频分布进行连通标记后，可以对跳频周期、中心频点、带宽等参数进行提取。传统的时频参数提取方法是对连通区域构造最小矩形边界，矩形边界可用向量(x，y，L，H)表征，x和y表示左下角的横、纵坐标，L和H表示x轴长度和y轴长度，则信号时频数据可以提取为起始时间x、结束时间x+L、跳频周期L、中心频点y+H/2、带宽H，如图4所示。

图4 信号时频参数提取示意图Fig. 4 Extraction of time-frequency parameters of signal

2.3 连通区域优化

信号时频分布的连通区域形成后，由于还存在定频、斜变干扰，以及去噪引起的信号连通断裂的情况，影响后续的时频参数提取，因此还需要对连通区域进一步优化。

（1） 连通区域片段关联

在信噪比较低的条件下，采用基于能量统计的自适应阈值噪声去除方法会使部分信号区域的幅度置0，从而造成同一类信号连通区域的断裂，需要根据断裂片段的特征相似性对其进行关联，然后完成拼接。源于同一类信号的断裂区域关联条件包括中心频率的相似性、带宽的相似性和时间接续性（即前一段信号连通区域的结束时刻与后一段信号连通区域的开始时刻在一个较小的范围内）。

设第i个信号段的中心频率为yi+Hi/2，终止时刻为xi+Li，带宽为Hi；第j个信号段的中心频点为yj+Hj/2，起始时刻为xj，带宽为Hj，满足前后信号连通区域片段的关联条件为

关联门限设置为Δt= 10，ΔH= 1，Δf= 5，将符合关联条件的信号连通片段之间的时频幅度设置为前一信号片段终止时刻幅度和后一信号片段起始时刻幅度的均值，可表示为

完成断裂区域的幅度填充后，则完成了不同连通区域片段的关联和拼接。

（2） 连通区域的干扰抑制

由于信号时频分布中存在定频、斜变信号干扰，容易与目标信号（跳频信号）发生碰撞，导致连通区域形状的畸变。干扰和跳频信号在连通区域标记图上的分布如图5 所示，最终产生较大的时频参数估计误差。

图5 干扰和调频信号连通区域标记分布图Fig. 5 Label distribution map of interference and frequency-hopping signals connected region

观察定频和斜变信号干扰的分布特征可以发现，2 类干扰与目标信号的连通区域标记分布有较大差异。其中，定频信号干扰在固定频率范围内的较长时段内连续分布，即时间轴占比率非常高，而跳频信号时间轴占比率较低；斜变信号干扰在连通区域形成的最小矩形边界中占零比非常高，而跳频信号占零比相对较低。基于以上分析的特征差异，可对连通区域标记分布图进行干扰抑制。

1） 定频干扰抑制

对所有连通区域进行参数提取，当提取的跳频周期满足Li≥Lmax（Lmax为已知跳频信号数据库中的最大跳频周期）时，则判断该连通区域为定频干扰，将其所在区域置0。

2） 斜变信号干扰抑制

首先对所有连通区域计算整体占零比，如果大于一定范围时，则该连通区域内可能存在斜变信号，可表示为

式中：Δn= 20%。

对满足式（9）的连通区域计算每一行的占零比，行占零比大于80%的判为斜变信号，将非0 位置的信号置0。

2.4 多目标信号混叠下的参数提取

由于不同跳频信号的出现时刻（起始时刻）、跳频周期、中心频率和带宽等参数的差异，可能在时频分布上存在时间和频率维的混叠，造成连通区域的变形，使得参数提取发生非常大的误差，其示意如图6 所示。

图6 多跳频信号混叠下的连通区域标记分布图Fig. 6 Label distribution map of connected regions under aliasing of multi-frequency-hopping signals

虽然2 个跳频信号在时间和频率维度上发生了混叠，但由于去噪后的时频分布矩阵保留了信号幅度信息，且混叠区2 个跳频信号幅度明显大于非混叠区的单个信号幅度，因此可以利用幅度的突变性来重构不同跳频信号的连通区域，从而分离出不同跳频信号，更准确地提取信号参数。多目标信号混叠下的参数提取步骤如下：

（1） 根据连通区域标记分布图确定最小矩形边界，并按照2.2节的方法提取参数向量(x0，y0，L0，H0)。

（2） 逐行计算后一时刻和前一时刻的幅度差，当幅度差有明显增大时，将后一时刻的点设置为混叠列边界点，可表示为

式中：σA为连通区域最小矩形边界内非零幅度值的均方根误差；k为尺度因子，这里取3。将满足式（10）的(x+ 1，y)点设置为混叠边界点（列方向），每一行计算完成后，得到混叠列边界的所有点。

（3） 逐列计算后一频率点与前一频率点的幅度差，当幅度差有明显增大时，将后一频率点的点设置为混叠行边界点，可表示为

将满足式（11）的(x，y+ 1)点设置为混叠行边界点（行方向），每一列计算完成后，得到混叠行边界的所有点。

（4） 完成混叠信号的连通区域重构后，重新进行连通区域标记，分离2 个连通区域，最后将带有幅度信息的二维时频图像进行二值处理，并根据二值图像信息提取时频参数，示意如图7 所示。

图7 连通区域重构后的参数提取示意图Fig. 7 Parameter extraction after reconstruction of connected regions

3 仿真结果及分析

3.1 信号分选

由于不同类型无人机采用的遥控信号（跳频信号）具有不同的跳频周期和调制带宽，因此，在对所有连通区域提取信号时频参数后，通过DBSCAN（density-based spatial clustering of applications with noise）聚类算法实现信号分选。该算法是一种经典的密度聚类算法，通过把类描述为紧密连接的最大节点的最大集合，把具有足够高密度区域以外的任意形状划分为一类［15］，其优势是不需要预设类别，运用该算法完成信号跳频周期和调制带宽参数的分选。

除了跳频周期和调制带宽可以作为分选识别的参数，不同跳频信号的出现时刻也是分选识别的重要参数。尤其是在多个同类型无人机目标条件下，信号具有相同的跳频周期和带宽，但信号出现时刻不同，因此在利用跳频周期和带宽完成聚类后，再利用信号出现时刻进行聚类，仍采用DBSCAN聚类方法。

3.2 仿真条件

（1） 场景1

跳频信号1（某型无人机遥控信号）：跳频周期为1 ms，跳频频率集{50，75，100，125，80，125，100，75，50，75，100，125，80，125，100，75，50，75，100，125} MHz，BPSK 调制带宽为1.8 MHz；

跳频信号2（其他外来无人机）：跳频周期为2 ms，跳频频率集为{190，70，140，120，155，30，60，115，90，180} MHz，BPSK 调制带宽为2 MHz。

干扰及噪声

定频干扰参数包括：干扰频率分别为143 MHz和162 MHz，带宽分别为0.8 MHz 和4 MHz。扫频干扰：起始频率为20 MHz，跳频斜率20 GHz/s，重复周期为250 Hz。噪声：高斯噪声，信噪比为6 dB。

对信号作短时傅里叶变换，使用窗长为4 096的Hamming 窗，1 024 为步长，画出时频图。信号如图8，9 所 示，图8 为 跳 频 信 号1 的 时 频 图，图9 为 跳频信号2 的时频图。

图8 跳频信号1 时频图Fig. 8 Time-frequency diagram of frequency-hopping signal 1

图9 跳频信号2 时频图Fig. 9 Time-frequency diagram of frequency-hopping signal 2

图10 为加入定频、扫频干扰得到的时频分布，图11 为混入噪声的时频分布。使用基于局部窗口能量统计的去噪方法，得到去噪后的时频分布如图12 所示。

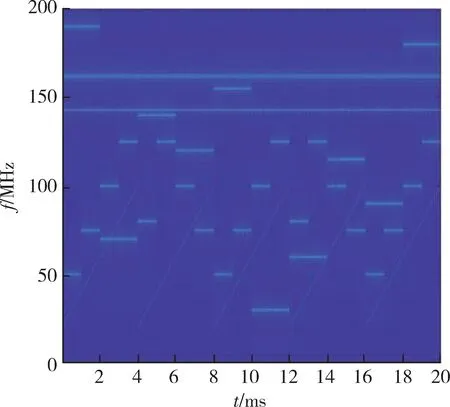
图10 混合信号时频图Fig. 10 Time-frequency diagram of mixed signal

图11 含噪信号时频图Fig. 11 Time-frequency diagram of noisy signal

图12 去噪后的时频图Fig. 12 Time-frequency diagram after denoising

对去噪后的时频矩阵进行连通区域标记，形成初步的连通区域标记分布图，然后进行连通区域优化，完成连通区域片段关联和拼接、干扰抑制、多目标信号混叠下连通区域优化，得到如图13 所示的修正后的二值化连通区域标记图。

图13 修正后的连通区域标记图Fig. 13 Label map of connected regions after correction

针对每个连通区域提取其跳频周期、调制带宽和出现时刻，参数归一化后运用DBSCAN 算法进行聚类。邻域内样本分布的密集程度参数(ε，MinPts)设置为(0.02，1)，表示以聚类中心半径为0.01 的邻域内点的个数不少于1 个的聚类，根据聚类结果将信号分为2 类，如图14 所示。2 类信号的参数估计如表2 所示。

表2 两组连通区域参数统计值Table 2 Parameter statistics of two groups of connected regions

图14 带类别信息的时频矩阵连通区域标记图Fig. 14 Label map for connected regions of timefrequency matrix with class information

此时与原始信号参数设置进行对比，可以采用决策树的思想对每个参数进行判断，从而判断分选出跳频1 信号和跳频2 信号。

（2） 场景2

跳频信号1：跳频频率集、跳频周期和带宽同场景1；

跳频信号2：跳频周期和带宽同场景1，跳频频 率 集 为{190，74，140，124，155，30，60，124，74，180} MHz。

在跳频信号中加入定频、扫频干扰和噪声（参数同场景1）得到的时频分布如图15 所示，分别采用基于局部能量统计方法去噪，采用本文提出的改进连通区域标记方法完成连通区域的优化和参数提取，最后采用DBSCAN 算法进行聚类，得到如图16，17 所示的连通区域标记图和类别信息。2 类信号的参数估计如表3 所示（这里仅列举平均跳频周期和平均带宽参数的统计值）。

表3 2 组连通区域参数统计值Table 3 Parameter statistics of two groups of connected regions

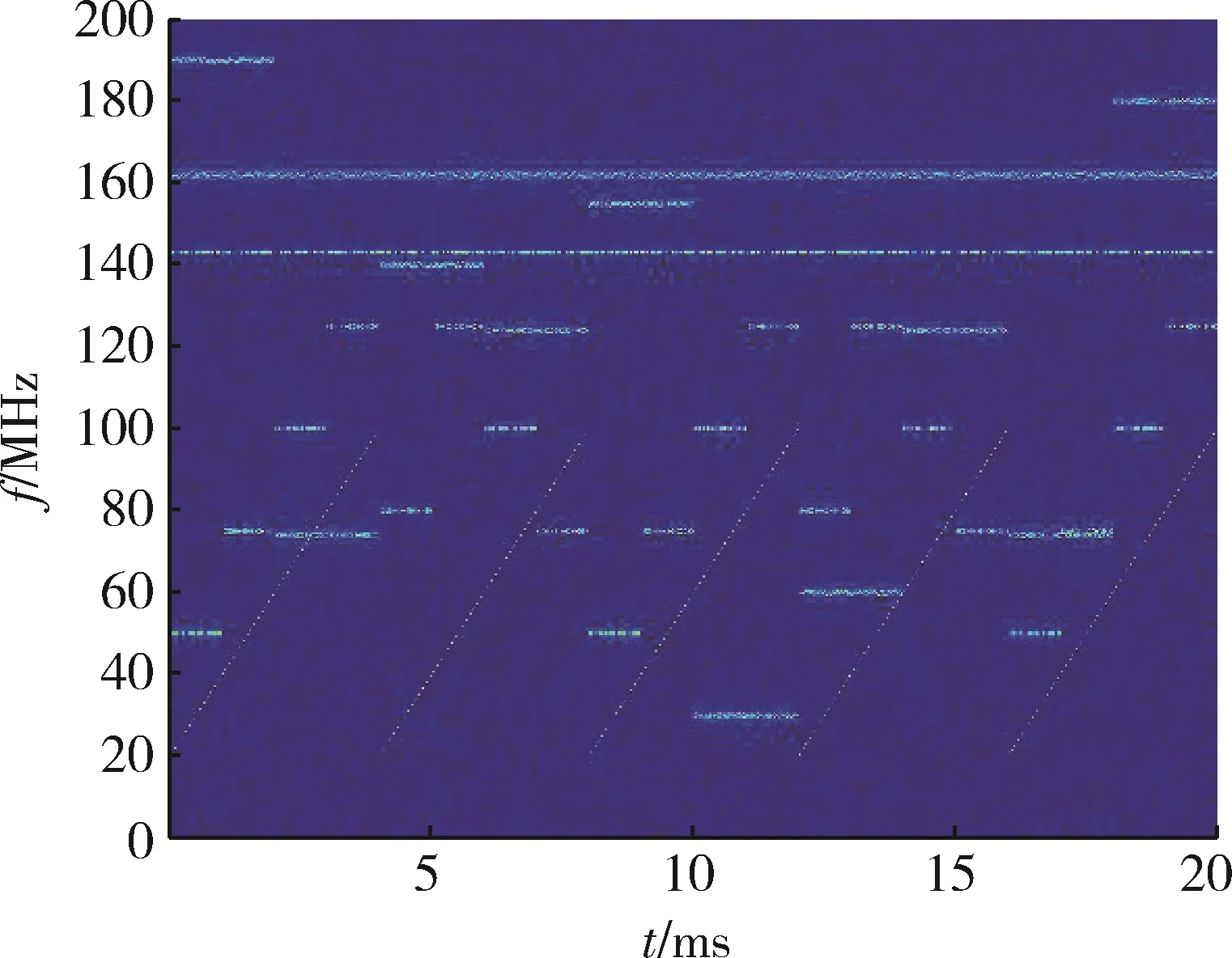
图15 跳频+干扰+噪声混合信号时频图Fig. 15 Time-frequency diagram of mixed signal containing frequency-hopping， interference，and noisy signals

图16 修正后的连通区域标记图Fig. 16 Label map of connected regions after correction

图17 带类别信息的时频矩阵连通区域标记图Fig. 17 Label map for connected regions of timefrequency matrixes with class information

（3） 场景3

跳频信号1（某型无人机遥控信号）：跳频频率集、跳频周期和带宽同场景1；

跳频信号2（外来无人机遥控信号1）：跳频频率集、跳频周期和带宽同场景1；

跳频信号3（外来无人机遥控信号2）：跳频周期和带宽同跳频信号2，跳频频率集为{165，130，75，110，155，45，80，135，60，120} MHz。

在跳频信号中加入定频、扫频干扰和噪声（参数同场景1）得到的时频分布如图18 所示。

图18 跳频+干扰+噪声混合信号时频图Fig.18 Time-frequency diagram of mixed signal containing frequency-hopping，interference， and noisy signals

采用本文提出的改进连通区域标记方法完成连通区域的优化和参数提取，最后采用DBSCAN 算法进行聚类，得到如图19，20 所示的连通区域标记图和类别信息。

图19 修正后的连通区域标记图Fig. 19 Label map of connected regions after correction

图20 带类别信息的时频矩阵连通区域标记图Fig. 20 Label map for connected regions of timefrequency matrixes with class information

3.3 不同方法的性能比较

2 种方法比较：基于连通区域标记的信号分选法［16］和本文提出的改进连通区域标记分选法。

基于连通区域标记的信号分选法：基于整体能量统计的自适应门限去噪+常规连通区域标记+信号拼接和拆解（连通区域修正）。

本文提出的改进连通区域标记分选法：基于局部能量统计的自适应门限去噪+常规连通区域标记+改进的信号拼接和拆解+信号混叠条件下的连通区域修正。

比较的性能指标包括参数（平均跳频周期、平均带宽）估计误差和目标正确识别概率。

采用1 000 次蒙特卡罗仿真统计平均跳频周期、带宽参数估计误差，并在不同信噪比条件下统计目标无人机遥控信号（跳频信号2）的正确识别概率。2 类方法的参数估计误差如表4 所示。

表4 不同场景下2 种方法的参数估计误差比较Table 4 Parameter estimation errors of two methods in different scenarios

从表4 结果可以看出，3 个场景下，本文提出的改进连通标记方法提取的参数相对误差明显小于常规连通标记法。其中，场景1 下的性能提升是由于改进的连通标记法进行了连通区域片段关联和干扰抑制，使得整个时频分布的连通图更完整和干净。场景2 和3 下的性能提升是由于采用了基于时频幅度差异的连通区域重构，将混叠在一起的跳频信号进行了连通边界区分，从而使参数估计更加精确。

图21 为多目标跳频信号混叠（场景2 和3）环境下，采用1 000 次蒙特卡罗仿真，不同信噪比的类别2 跳频信号（外来无人机遥控信号1）的识别概率。可以看到，信噪比对跳频信号识别影响明显，识别概率随着信噪比增加而提高。常规连通标记方法下，为达到高识别概率（0.9），信噪比分别需达到5 dB 和7dB 以上，而采用了改进连通区域标记方法后，信噪比只需3 dB 和4.2 dB 以上。且由于参数估计精度更高，在不同信噪比条件下，改进连通区域标记方法的目标识别概率均高于常规方法，能够更好地识别出外来无人机的遥控信号。

图21 类别2 跳频信号的识别概率Fig. 21 Recognition probability of Class 2 frequency-hopping signal

4 结束语

本文针对干扰环境下无人机跳频遥控信号的分选识别问题开展了研究。首先考虑到噪声环境的不均匀性，设计了基于局部能量门限统计的去噪方法。然后对去噪后时频矩阵进行连通区域标记，在常规连通区域标记方法的基础上，对连通标记方法进行了改进。根据连通区域片段的相关性设计了片段关联方法，完成信号的拼接。根据定频、扫频干扰的时频分布特征设计了干扰抑制方法，并在多目标跳频信号混叠情况下提出了基于幅度差异的连通区域重构。最后根据优化的连通区域标记实现对跳频信号的参数估计和分选识别。仿真实验表明，本文方法在无多目标混叠和有多目标混叠2 种场景下，信号时频参数估计精度明显高于常规连通标记方法，对目标跳频信号的正确识别率也明显提高，能够较好地检测识别外来无人机。