基于辅助阵元的幅相误差和DOA 同时估计算法 *

赵海洲，王小哲，孙晨，郭艺夺

（空军工程大学 防空反导学院，陕西 西安 710051）

0 引言

阵列扰动［1-3］作为在实际中常见的一种非理想条件，会严重影响信号处理的性能。考虑到阵列阵元在加工等流程以及实际中的应用，可将阵列扰动总结为3 类：阵元互耦［4-5］、阵元幅相误差［6-7］和阵元位置误差［8-9］。其中，阵元幅相误差在现实阵列中是普遍存在的，也是各国学者研究波达方向（direction of arrival，DOA）估计时考虑的一个热点问题。

对于阵元幅相误差的校正，初期提出的算法均需要校准信源作为先验信息［10-11］。为了实现阵元幅相误差的自校正，文献［12-13］利用子空间类算法循环估计信号DOA 和幅相误差，通过不断地迭代最终估计出了幅相误差。该算法虽然实现了阵元幅相误差的自校正，但多次循环迭代带来的高复杂度使得算法并不实用。为了避免出现迭代过程，Paulraj 和Kailath 利用ULA 接收信号协方差矩阵具有Toeplitz 矩阵结构的特征，提出了一种基于子空间变换的幅相误差估计算法［14］，但是该算法需要对协方差矩阵上三角的每一条对角线进行标定，计算过程烦琐。针对这一问题，文献［15］提出了一种基于协方差矩阵不同对角线的简化标定算法，实现了低复杂度的幅相误差校正。但是这2 类算法只适用于均匀线阵，为了解决受阵列结构限制的问题，文献［7］中针对二维阵列提出了一种新型的基于子空间的幅相误差校正算法。但是现有算法普遍计算复杂度偏高，且大多不能同时实现幅相误差和DOA 的同时估计。

为了解决以上问题，本文提出了一种基于少量精确校正辅助阵元的幅相误差和DOA 同时估计算法。该算法能够实现信源功率存在较大差异时，高精度的误差和角度的同时估计。

1 信号模型

1.1 均匀线阵信号模型

通常，理想阵列可认为是阵元间距为半波长的均匀线阵（uniform linear array，ULA），即阵元间距d满足d=λ2，其中，λ为波长。假设L个远场窄带信号入射到阵元数为M的ULA 上，如图1 所示。

在图1 中，θl为第l个入射信号的角度。此时，可以写出该阵列在θl方向上的导向矢量为

式中：ϕl=2πdsin(θl)λ，l= 1，2，…，L。

假设第l个信号在k时刻辐射到阵列上的波形为sl(k)，每个信号相互独立。在不考虑阵元之间存在误差的情况下，在k时刻阵列接收到的数据可以表示为

式中：n(k) ∈CM×1表示噪声向量，一般噪声设为加性高斯白噪声，且与入射信号相互独立。

由式（2）可得接收信号的协方差矩阵为

但在实际中，协方差矩阵往往都难以准确获得，一般都用采样协方差矩阵（sampling covariance matrix，SCM）来代替，其表达式为

式中：K为采样快拍总数。

1.2 阵元幅相误差下的信号模型

假设阵列中第m个阵元的幅度误差和相位误差分别为αm，φm，则阵列的幅度误差矩阵和相位误差矩阵分别为

式中：diag{·}表示对角化运算符；一般以第1 个阵元作为参考阵元，即有α1= 1，φ1= 0。

在考虑阵元幅相误差时，模型（2）改写为

此时，受误差影响下的导向矢量为

2 幅相误差和DOA 同时估计算法

2.1 算法原理

根据矩阵运算，式（8）可以进一步写成

式中：Ψ=ΦΓ为幅相误差矩阵；ϕ=diag(Ψ)为幅相 误 差 向 量；Tϕ(θ) ∈CM×M的 第m列 表 示 为Ema(θ)，Em∈CM×M表示为

由子空间基本原理［16］知，在存在幅相误差时可推出：

由于Un秩为M-L，因此对于任意角度θ都有Qϕ(θ)为奇异矩阵。若幅相误差矩阵中的元素出现若干相同元素，则在满足一定条件时获得的对应于非入射信号方向的过渡矩阵将会是满秩矩阵，此时便可利用这一性质来估计幅相误差。

对于幅相误差矩阵中出现若干相同元素这一假设，可通过在阵列的一端放置少量已校正阵元或幅相误差近似的阵元来实现。当阵列中增加的已校正阵元数为P-1 时，阵列的幅度误差和相位误差系数有

此时，Γ和Φ可重写为

式 中 ：ΓP≜diag{αP，αP+1，…，αM}；ΦP≜diag{ }ejπφP，ejπφP+1，…，ejπφM。

此时，幅相误差矩阵和幅相误差向量分别可以表示为

重新定义式（10）为

式中：G=M-P+ 1。

可得

因此，式（11）可重写为

式中：Qϕ(θ) ∈CG×G。

当G≤M-L，即L≤P- 1 时，一般角度θ时可以认为Qϕ(θ)是一个满秩矩阵。但是当θ为入射信号的DOA 时，也即θ=θl(l= 1，2，…，L)，根据第1 节的分析，Qϕ(θ)则会成为一个奇异矩阵。此时由式（20）可知，ϕP是Qϕ(θ)中0 特征值对应的特征向量。

因此，可构造谱函数为

对式（21）或式（22）进行谱峰搜索，得到前L个最大谱峰对应的位置即可得到入射信号的角度估计值，并可计算出对应方向̂的过渡矩阵Qϕ(̂)。由于幅相误差矩阵是与方向无关的，因此ϕP可以估计为

式中：ulmin为Qϕ(̂)最小特征值对应的特征向量；(ulmin)1表 示ulmin的 第1 个 元 素。

当入射信号的SNR 较低时，估计得到的角度会有较大误差，此时利用对应的过渡矩阵Qϕ(θ)估计ϕP时会有较大的误差。因此，当多个入射信号之间的功率相差过大时，在最终估计ϕP时对得到的过渡矩阵进行筛选，选择较大功率信号对应的过渡矩阵Qϕ(θ)来估计ϕP会提高估计精度。此时有2 种策略：

（1） 选择最大谱峰对应的过渡矩阵来估计ϕP

通过谱峰搜索获得的最大谱峰对应着功率最强的入射信号，选择此谱峰对应的过渡矩阵Qϕmax(θ)用来估计ϕP，此时式（23）重写为

式中：umax-min为Qϕmax(θ)最小特征值对应的特征向量。

（2） 剔除掉对应最小谱峰的过渡矩阵来估计ϕP

假设获得的最小谱峰对应的过渡矩阵为Qϕ(̂)，在后续 估 计ϕP时 忽略矩阵Qϕ(̂)，此 时 式（23）重写为

2.2 算法步骤

综上，对所提的阵元幅相误差和DOA 同时估计算法总结如下：

第1 步：估计协方差矩阵，计算噪声子空间Un；

第2 步：计 算 变 换 矩 阵Tϕ(θ)，构 造 谱 函 数Pdet(θ)；

第3 步：谱峰搜索，找到L个最大谱峰的位置，估计角度，计算̂ 对应的过渡矩阵Qϕ(̂)；

第4 步：选择合适的过渡矩阵进行特征分解，估计幅相误差向量。

需要注意的是，这些是建立在假设L≤P- 1 的基础上推导完成的。虽然此方法可以实现幅相误差和DOA 的同时估计，但在应用中算法自由度受到辅助阵元数的限制，而且将多个已校正阵元或幅相误差近似的阵元作为辅助阵元接收信号意义不大，因此，本方法还是更适合用于前期的阵列校正中。不难发现，所提算法对于阵列的排布并无特殊要求，也即该算法也可适用于非均匀线阵。同样地，通过修改导向矢量的形式，该算法也可拓展到二维阵列中去。此外，为了保证DOA 估计无模糊，辅助阵列的布置通常设置为阵元间距半波长的ULA。

3 计算机仿真

此仿真主要分析所提的算法在阵元幅相误差下DOA 和幅相误差估计性能。仿真条件设置为：待校准阵列为最小阵元间距为0.5、阵元数为12 的ULA，波长λ= 1；辅助阵列是由4 个已校准阵元构成的ULA，放置在待校准阵列一端，且与待校准阵列共同组成阵元数为16 的ULA。蒙特卡罗实验次数为100。

实验1： 阵元幅相误差和DOA 同时估计算法的有效性验证

此仿真主要验证所提阵元幅相误差和DOA 同时估计算法的有效性。为了更普遍地验证算法性能，仿真中设置幅度和相位误差分别服从如下分布：

式中：δm和ηm均为相互独立且均匀分布于[-0.5，0.5]中的随机变量；σα和σφ分别为δm和ηm的标准偏差，分别设置为0.1 和15°。入射信号角度分别为-30°，-10°，40°，对应的SNR 均为10 dB，采样快拍数为200。仿真得到的空间谱和幅相误差估计值分别如图2 和表1 所示。

表1 阵元幅相误差估计值Table 1 Estimated sensor gain-phase errors

图2 空间谱Fig. 2 Spatial spectrum

从图2 中可以看出，所提出的阵元幅相误差和DOA 同时估计算法获得的空间谱可精准地估计出入射信号的DOA；从表1 中可看出，所提算法能够精确地估计出幅相误差，也即所提算法有效地实现了阵元幅相误差和DOA 的同时估计。

实验2： 阵元幅相误差和DOA 同时估计算法的DOA 估计性能

此仿真主要为了分析所提阵元幅相误差和DOA 同时估计算法DOA 估计的性能，以同为子空间类算法的MUSIC（multiple signal classification）算法和DOA 估计值 的CRB（Cramér-Rao bound）作为对比。假设阵列接收到3 个信号，角度分别为-30°，-10°，40°，SNR 均为10 dB。在分析所提算法DOA估计性能与SNR 变化的关系时，快拍数设置为200，SNR 从-10 dB 到30 dB 变化，其余参数保持不变；在分析所提算法DOA 估计性能与快拍数变化的关系时，SNR 设置为10 dB，快拍数从50 到400 变化，其余参数保持不变。仿真结果如图3 所示。

图3 DOA 估计值的RMSE 与SNR 的关系Fig. 3 Relationship between RMSE and SNR of estimated DOA

由图3 可知，随着SNR 的增加，提出的阵元幅相误差和DOA 同时估计算法的DOA 估计精度均有所增加；但在低SNR 时，所提算法的DOA 估计精度低于MUSIC 算法，这是由于所提算法在实现DOA 和阵元幅相误差同时估计时，利用的是噪声子空间构建的一个更小维度的过渡矩阵，在低SNR 时，难以准确估计出噪声子空间，此时所提算法利用更低维度的矩阵便难以获得更高精度的DOA 估计值。

实验3： 阵元幅相误差和DOA 同时估计算法阵元幅相误差估计性能

此仿真主要为了分析所提阵元幅相误差和DOA 同时估计算法对阵元幅相误差的估计性能。以文献［10］中提出的基于子空间的阵元幅相误差估计算法作为对比算法，同时仿真中还给出了阵元幅相误差估计值的CRB。为了方便，将采用式（21）和式（22）的所提算法分别称为“所提算法1”“所提算法2”。为充分展示所提算法在不同入射信号功率下对阵元幅相误差的估计性能，假设入射信号为1 个SNR 为10 dB、入射角度为-10°的期望信号和2个干噪比（interference-to-noise ratio，INR）为40 dB、入射角度分别为-30°和40°的干扰信号。在分析所提算法幅相误差估计性能与SNR 变化的关系时，快拍数设置为200，SNR 从-10 dB 到50 dB 变化，其余参数保持不变；在分析所提算法幅相误差估计性能与快拍数变化的关系时，SNR 设置为10 dB，快拍数从50 到400 变化，其余参数保持不变。蒙特卡罗实验次数为100，仿真结果如图4 所示。

图4 阵元幅相误差估计值的RMSE 和SNR 的关系，INR =40 dB，K = 200Fig. 4 Relationship between RMSE and SNR of estimated sensor gain-phase errors INR = 40 dB， K = 200

如图4 所示，相较于对比算法，在存在一个低SNR 信号时，也即多个入射信号存在较大的功率差时，提出的2 种算法对幅度误差和相位误差的估计性能接近，虽然2 种算法均更加靠近幅度误差和相位误差估计值的CRB，但所提算法2 估计得到的幅相误差精度更高。随着信号SNR 的增加，所提的2种算法对幅相误差的估计精度较对比算法均有所下降，这是由于此时所有信号功率接近，每一个信号均为可用信号，利用越多的信号来估计幅相误差，估计的精度就越高。随着SNR 的进一步增大，高功率信号对幅相误差估计性能的改善更为明显，因此所提算法1 的估计精度再次超越对比算法，更为接近CRB。

实验4： 算法运行时间比较

为了直观地看出本文所提算法在运算量方面的优势，图5 给出了P=2，L=100，SNR=10 dB 时，所提算法和文献［10］中对比算法的运行时间随阵元数变化曲线。从图5 中可以看出，当阵元数较小时，所提算法的运行时间与对比算法的运行时间基本相当。但随着阵元数的增大，所提算法在运算量上的优势逐步得到体现。

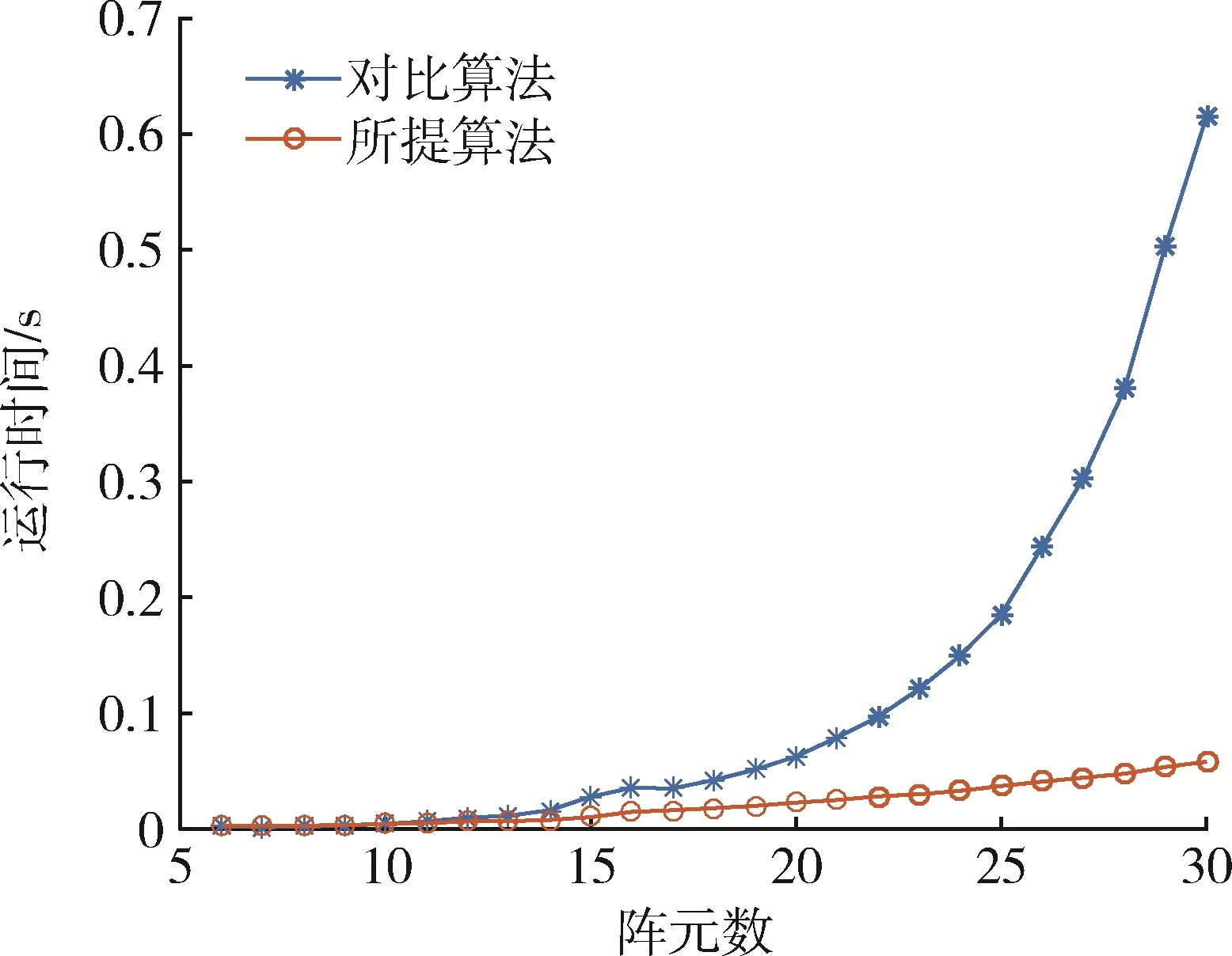
图5 2 种算法的运行时间对比Fig. 5 Comparison of running time between two algorithms

4 结束语

本文通过设置少量的辅助阵元，利用阵元幅相误差矩阵为对角矩阵的结构特点，并基于子空间类算法的原理，提出了一种阵元幅相误差和DOA 同时估计算法。针对信号功率相差较大问题，给出了2 种不同的解决策略，并取得了较好的效果。计算机仿真结果表明：所提算法能够以较高的精度同时估计出幅相误差和目标的DOA，尤其在存在功率差异较大信号时，能够显著提高对误差的估计精度。