改进STL分层算法在机械零件3D打印中的应用研究①

陈鸿寿

(福州外语外贸学院艺术与设计学院,福建 福州 350202)

0 引 言

3D打印由于其自身特性,能更好满足不断提升的机电产品生产标准[1]。但这种方法生产的产品质量由于STL模型分层效果不佳原因,依然会受到显著影响。为解决这个问题,技术专家们开展过大量研究。田仁强学者团队提出了一种应用于增材制造中STL模型三角面片法向量的自动分层算法,测试实验结果显示,经过该算法处理后,STL模型中轮廓变化明显的区域分层更为精细[2]。韩兴国等人提出一种针对具有复杂曲面的零件的截面轮廓生成算法,仿真测试结果表明,按照该算法处理后的模型生产的金属叶片精度更高[3]。可见,为解决这类问题开展过大量研究,但分析STL文件标准下的模型网格面片信息间联系并以此为基础改进分层方法的研究还很少见,而这种改进思路也可能使得3D打印的产品质量得到大幅提升。

1 面向机械零件3D打印建模的改进STL分层切片算法设计

1.1 融合层厚关联的模型网格面片分块方法设计

当前传统的分层算法在处理复杂结构的3D大于模型上处理效率较为低下,因此现在提出基于网格面片环结构的改进STL模型分层算法[4-5]。下面先设计改进算法中的网格面片分块方法。以长方体为例,构建出STL模型适用分层坐标系,见图1。

图1 STL模型分层坐标系示意图

图1中Ω代表分层平面,Pi(xi,yi,zi)(i∈[1,8])代表待分层的长方体的各顶点。根据该坐标系可求得包围盒在z向坐标轴的高度z。而且根据精度要求,还能确定模型的分层厚度di=zstroke/n、分层层数n=ceil(zstroke/di),其中ceil()为下取整函数,以及第i层的切片平面高度zi,(i=1,2,…,n)。根据上述方法,同样可以求出包围盒在x,y方向的长度xstroke,ystroke,至此分层的行程规划完成。凸包围盒的底面被作为初始的切片平面Ω1,且其中含有P2,P4,P6三个顶点,因此Ω1可用式(1)方程描述。

(1)

使用以上方法,可以创建出STL模型的全部切片平面,从而获得切片平面集Ω。STL模型的三角网格面片是沿着分层方向排列的,经过同步分块处理的STL模型网格面片见图2。

图2 同步分块处理后的网格面片示意图

图2中Di(i=1,2,…,n-1)意为被切片平面分割出的各区域,切片平面Ωi的高度值为zi。同步分快处理后的STL模型三角网格面片主要由两部分组成。第一步部分用于判断每个三角面片的所属区域,第二部分则用于处理三角面片与多个区块切片平面相交的情况。遍历完所有三角面片后,即可确定每一切片平面的相交网络面片集。

1.2 构建基于邻接拓扑的网格面片环

传统的STL模型不能很好地表达相邻三角面片的邻接关系,所以有必要重构三角面片之间的邻接拓扑关系[6]。假设模型中存在顶点v,其邻接顶点被称为该顶点的环邻域点,它的n环邻域点可表示为rg(v,n),全部的环邻域顶点为Nn(v)或{rg(v,i)}0≤i≤n环绕面片顶点v的面片表示为rg(f,n)。三角网格化后的STL模型中,每条边至多可属于两个面,且任意相邻邻接面最多可以有一条公共边[7]。将平面多边形环顶点依次连接,见构成一种特别的拓扑结构,其中首尾顶点重合如图3所示。

建立网格面片环过程中,首先需要建立STL模型中三角网格面片集之间的拓扑关系,将某面片作为初始面片,查找它的1环领域邻接面片,并从中选出一个面片作为构建面片环的递归邻接面片,再选出后者的另外一个邻接面片作为后续的下一个构建面片并重复以上操作,直到构建出完整的面片环。完成面片环构建后,下一步是确定面片的所属区域,从而获得它们的相交面片集Mi(i=1,2,…,n)。但由于某些面片在分层方向存在zj,h=zj,max-zj,min≥2di关系,它们会与多个切片平面相交,导致相邻切片平面被存储与相同面片的情况出现。对于一个所有切片平面存储完成的面片集Mi,构建出面片环后,需要计算出它的对应哈希链表,哈希表的散列算法见公式(2)。

(2)

式(2)中z1,zn,zj分别代表最小层、最高层、第j层的切片平面的高度值。构建网络面片环哈希链表且获取相邻三角面片公共邻接边的步骤如下。首先获取Qi的Mi并按面片排序对其编号。设定初始面片并记录到哈希链表Mi,1中,通过解码获得反向半边的编码,并求出它的raj(Mi,1,1)。从raj(Mi,1,1)中选出一邻接面片赋值给Loopi,1,并记录到哈希链表中,符号为Mi,2。同时还需记录半边与反向半边的公共邻接边li,1,1。下一步是递归查询当前面片,然后将其放置于Loopi,1中,并以Mi,j(j=1,2,...,n)标记,直到网格面片环构建完毕。

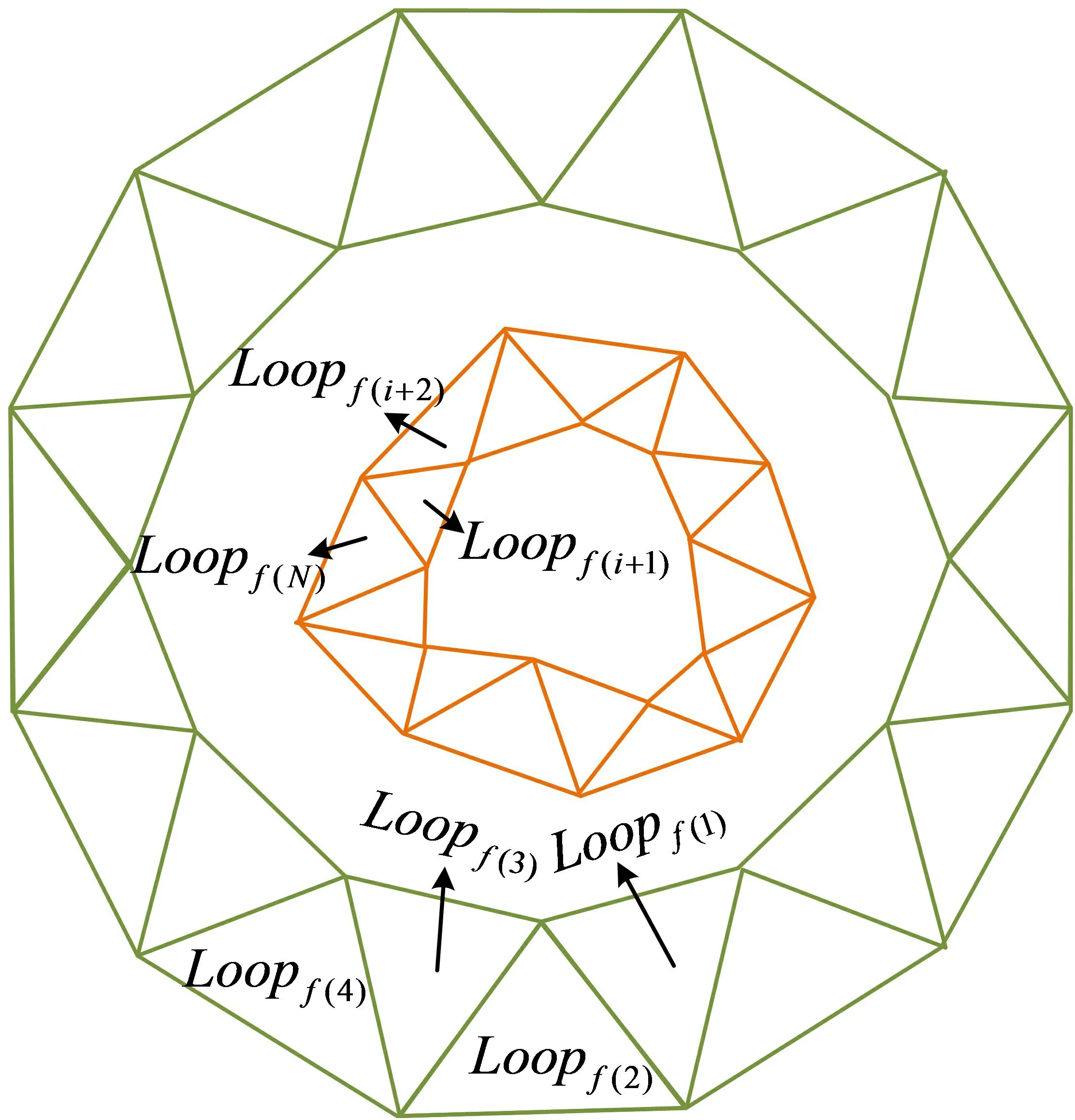
图3 三角网格化的STL模型面片环拓扑结构

1.3 改进STL分层切片算法设计

切片平面与三角面片的交点同时也是切片平面与STL模型的交点,且相交边均不低于两个[8]。在求这些交点时,只需要求解一次各切片平面相交中邻接边与切片平面交点。从而提高求解效率。切片平面Qi与和切片平面相交的邻接边li,j,k的交点坐标可按公式(3)求得。

(3)

式(3)中(x1,y1,z1)、(x2,y2,z2)分别为面片的两顶点v1,v2在空间直角坐标系中坐标值。观察式(2)可知,由于Qi的z轴数值zi与交点vp的z轴数值zp相等,就能计算出交点vp在x,y轴上的数值,具体的计算方法见式(4)。

(4)

至此基于网格面片环的STL模型改进分层切片算法构建完成,其运算步骤见图4。

图4 STL模型改进分层切片算法流程图

如图4所示,优化后的机械零件STL模型输入算法后,需要首先确定算法的运行参数,即分层厚度或分层层数,然后将三角面片分块化,获得切片平面的相交三角形网格面片集,并基于当前切片平面的相交面片集邻接拓扑关系,构建出网格面片环,并将其存储到哈希链表中。所有切面均完成以上操作后,再构建出相邻面片的公共邻接边,然后按照计算出的公共邻接边与切片平面交点,获得所有切片平面的截面轮廓交点集合,最后连接各切片平面的截面轮廓点,即可得到分层处理后的由多个切片平面组成的平面界面轮廓多边形环。

2 改进算法在机械零件3D打印中的应用测试

此次研究中选用关节内球作为3D打印的对象。文献[9],文献[10],文献[11]设计的机械零件STL模型分层算法具有较大的实用价值,将其作为对比研究设计方法性能的对比算法。测试中选用经过各分层算法处理后的模型打印实体的轮廓算数平均偏差和轮廓最大高度,以及分层切片的耗时作为评价指标。实验结束后,使用表面粗糙度测量仪测量3D打印的机械零件表面粗糙度数值。完成实验后,分析各算法的轮廓算术平均偏差数值,见图5。

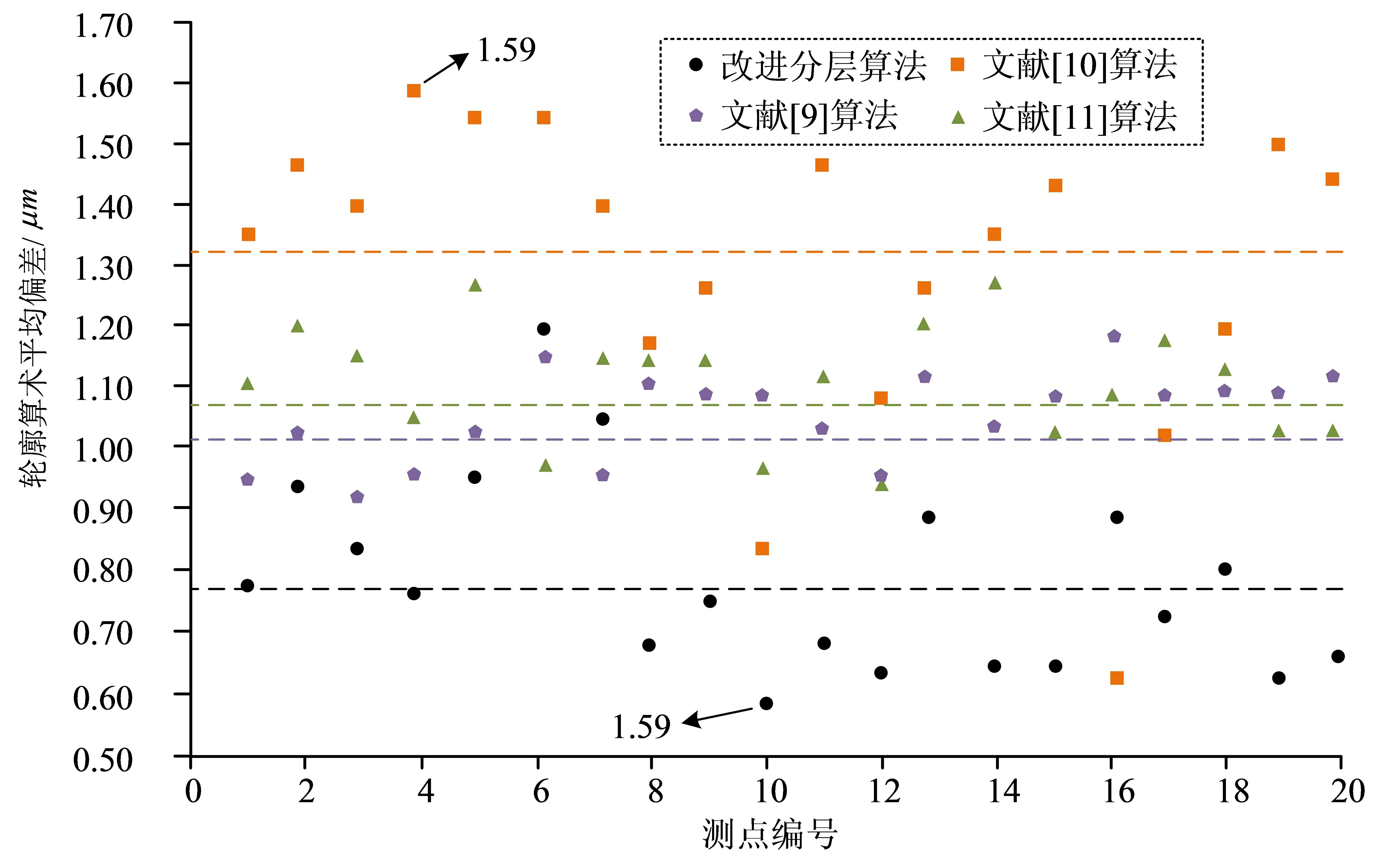
图5 3D打印机械零件的轮廓算术平均偏差对比

图5中“改进分层算法”指研究设计出的分层算法。虚线用于代表不同算法所有测点轮廓算术平均偏差值的均值,观察图5可知,改进分层算法轮廓算术平均偏差整体最小,其数值的均值为0.77,而文献[9],文献[10],文献[11]设计算法的该指标分别为1.01,1.07,1.32。再分析各算法的轮廓最大高度数值,见图6.

图6 3D打印机械零件的轮廓最大高度对比

观察图6可知,从轮廓最大高度指标的角度来看,改进分层算法处理后的打印模型表面粗糙度依然是所有对比方法中最低的,其15号测点的轮廓最大高度值最小,为1.12.文献[10]中的分层算法处理后的打印模型轮廓最大高度值整体最高,最大值在它的9号测点取得,为1.97。最后分析各分层算法对关节内球STL模型进行分层切片处理的耗时数据,见表1。

表1 3D打印机械零件的STL模型分层切片耗时对比

观察表1可知,当分层厚度分别为0.10mm,0.20mm,0.30mm,0.40mm时,改进分层算法分层平均耗时与最大耗时为,6.02s,3.17s,2.45s,1.98s与8.51s,3.83s,2.99s,2.67s,比耗时表现次之的文献[10]方法减少了0.52s,0.25s,0.28s,0.42s与1.34s,0.18s,0.57s,0.07s。

3 结 语

针对传统生产复杂机械零件过程中材料加工精度不足、加工成本高的问题。研究对3D打印方法中的STL模型分层切片算法进行优化设计。实验数据显示,研究设计出的分层算法轮廓算术平均偏差整体最小,其数值的均值为0.77,而文献[9],文献[10],文献[11]设计算法的该指标分别为1.01,1.07,1.32。整体上研究设计的改进分层算法处理后的打印模型表明粗糙度依然是所有对比方法中最低的。而且当分层厚度分别为0.10mm,0.20mm,0.30mm,0.40mm时,改进分层算法分层平均耗时分别为,6.02s,3.17s,2.45s,1.98s,低于对比算法。实验结果显示该研究提出的改进分层切片算法切片效率更高,打印出的零件表面偏差更小,更为光滑,在生产高精度机械零件中具有一定的应用价值。但由于研究条件所限,研究未能选用更多复杂机械零件开展实验,这也是后续实验所需注意的。