复合受力状态下T型砌块整浇墙刚度衰减研究①
汤旭冬, 赵 艳, 盛 叶, 黄 鑫, 胡 超
(1.福建农林大学交通与土木工程学院,福建 福州 350002;2.武夷学院土木工程与建筑学院,福建 武夷山 354300)
0 引 言
砌块整浇墙(Full Grouted Reinforced-Block Masonry Shear Wall 简称 FG-RBMW)是在配筋砌块砌体剪力墙(Reinforced-Block Masonry Shear Wall 简称 RBMW)的基础上,为提高该种结构的受力性能提出,其主要特征是采用预制的孔洞率不低于 45% 的混凝土空心砌块,在保证对孔率不低于 90% 的前提下经砂浆砌筑而成的墙体。该种墙体在水平和竖直方向均配置钢筋,孔洞内全部采用专用的混凝土100%灌实。
剪力墙作为配筋砌块砌体剪力墙结构体系的主要抗侧力构件,在水平力的作用下,试件刚度随着加载位移的增大而逐渐降低[1-5]。目前,国内外学者对RMBW结构刚度衰减规律做了大量研究。文献[6]认为增加轴压力对初始刚度的提升有一定的效果;同时设置构造柱对墙片的初始刚度提升作用更明显。文献[7]认为随着剪跨比的减小,试件的初始刚度增加,但衰减速率更快,表现出更明显的脆性特征;剪跨比越小,轴压比的变化对刚度影响越明显,与文献[6]的结论一致。文献[8]认为轴压比对刚度退化有较明显的影响,轴压比大刚度退化速度相对较快,与文献[9-10]得出的结论相似。文献[11-12]认为水平配筋率对初始刚度以及刚度衰减影响较小,但是过低水平配筋率会导致墙体刚度衰减过快,与文献[13]的结论一致。文献[13]进行了多种因素对墙体刚度退化的影响,其认为降低砖块高度、改善砌体的质量或者增加竖向配筋率都可以最大程度地降低刚度衰减速率。文献[14]通过对存在中央窗的墙体施加循环荷载,结果表明;开口的存在会增加刚度衰减的速率。文献[15]认为随着高宽比的增加,刚度退化略有减少。以上研究多以配筋率、轴压比、剪跨比等为研究对象,对灌芯材料的研究较少,而灌芯材料作为RMBW的重要组成,其属性对于墙体在往复荷载下的表现影响较大;另一方面,现有研究墙片多为一字型,加载方式为单向水平往复加载。对于复合受力下以及其它形状的墙体研究较少,而双向加载以及墙片形状的不同对墙体在加载过程中刚度变化有待研究。
根据墙体拟静力试验数据,分析复合受力状态下T型砌块整浇墙的刚度衰减规律,以此建立适用于此种墙体的刚度衰减方程,为此种体系整体结构的弹塑性反应分析提供理论基础。
1 墙体试件参数
研究的四个试件的编号和有关参数见表1。
2 刚度衰减方程
运用JGJ/T 101-2015 《建筑抗震试验规程》中规定的割线刚度方法,如式1所示。对试验中墙体的滞回曲线数据进行计算,得到不同位移时的刚度。根据灌芯材料不同对墙体刚度进行回归分析,得到刚度衰减方程。
(1)
式中,+Pi,-Pi为第i次正反两向峰值点荷载值;+Δi,-Δi为第i次正反两向峰值点位移值。
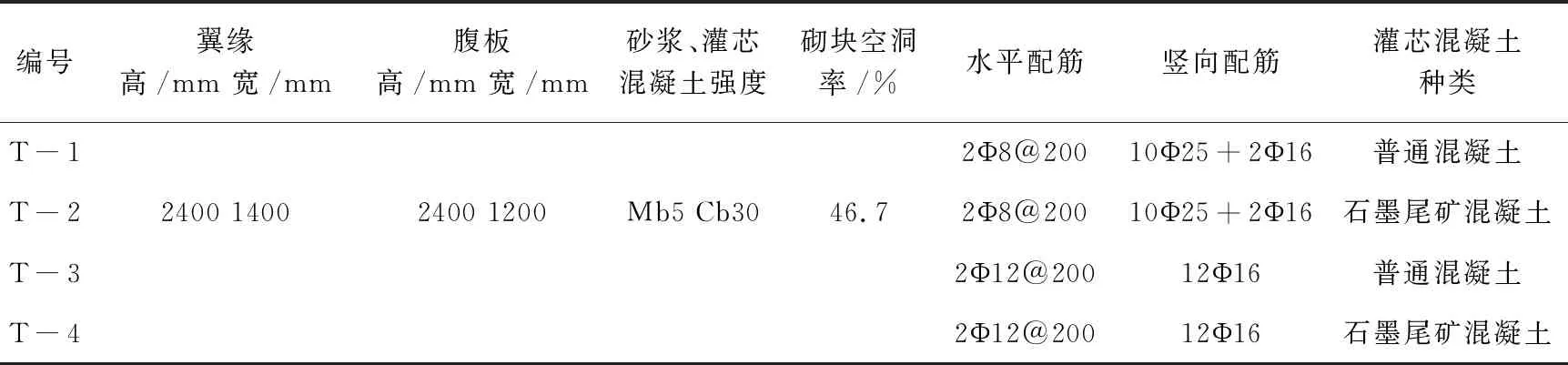
表1 试件参数
2.1 T1,T3墙片
T1、T3墙体的刚度计算结果如图1所示。由图可知,拟合曲线与试验结果吻合良好,表明指数函数可以表达墙体的刚度衰减规律。由于试验过程中T1墙体产生较大滑移,导致图1-b中试验数据离散较大,但拟合曲线也能较好的描述试验数据的刚度退化。
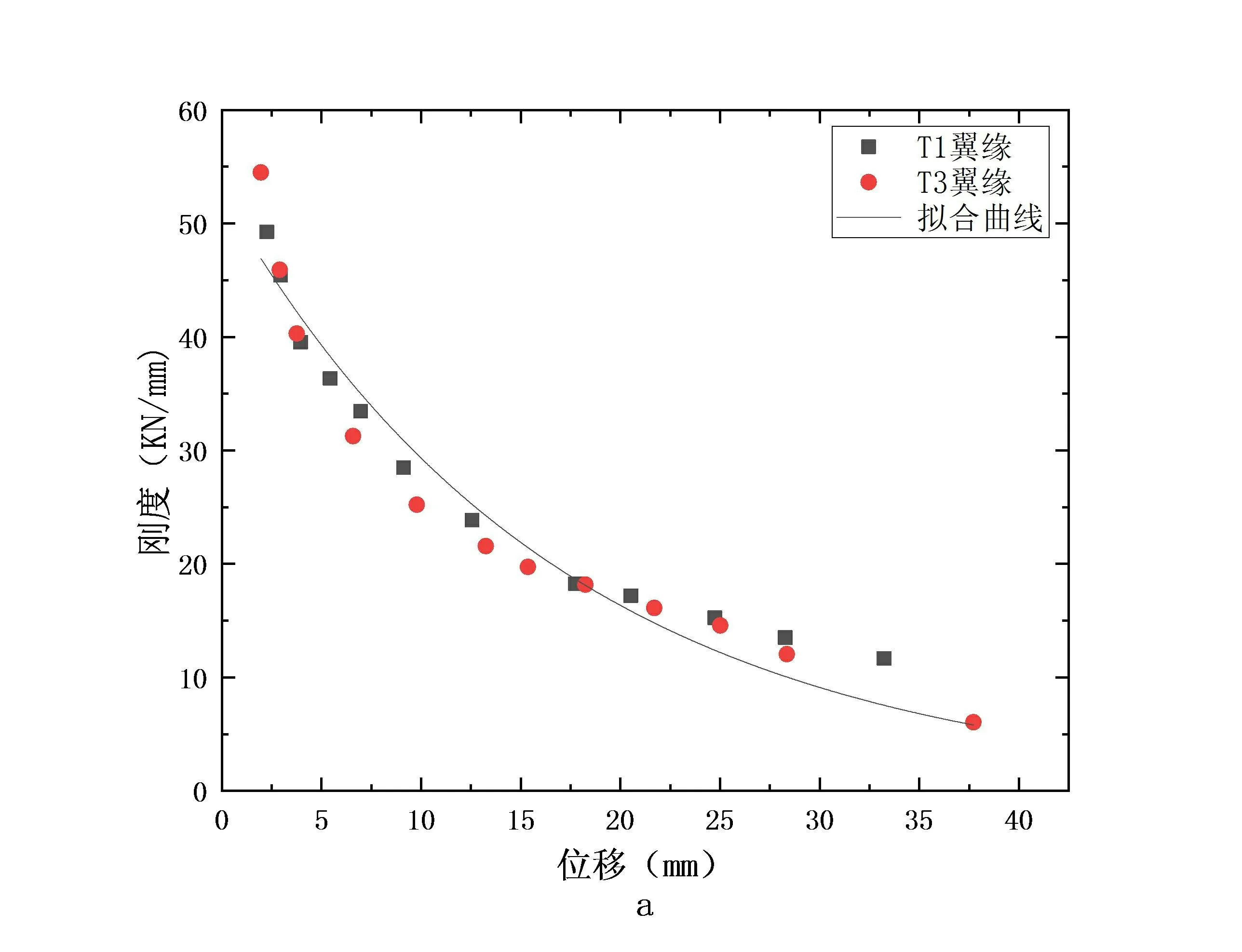
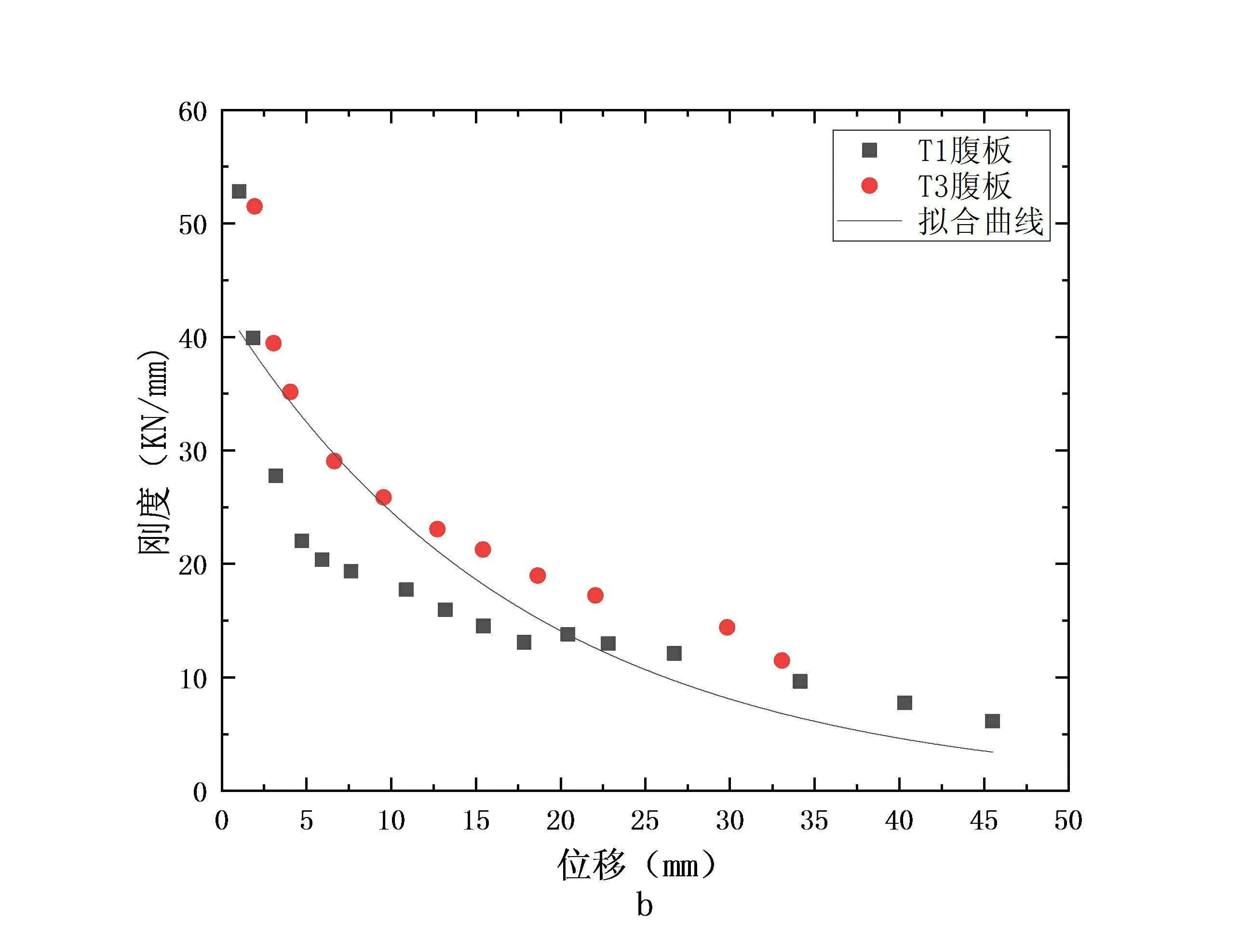
a-T1,T3翼缘;b-T1,T3腹板
对试验数据进行回归分析,得到T1,T3墙体翼缘的刚度衰减方程如式2所示:
K=e(-0.058Δ+3.96)
(2)
腹板的刚度衰减方程如式3所示:
K=e(-0.056Δ+3.76)
(3)
其中:Δ为各点的位移值。
2.2 T2,T4墙片
T2,T4墙体的刚度计算结果如图2所示,拟合曲线与试验结果吻合良好,验证了指数函数可以表达墙体的刚度衰减规律。对试验数据进行回归分析,得到T2,T4墙体翼缘刚度衰减方程如式4所示:
K=e(-0.075Δ+4.41)
(4)
腹板刚度衰减方程如式5所示:
K=e(-0.057Δ+4.21)
(5)
其中:Δ为各点的位移值。
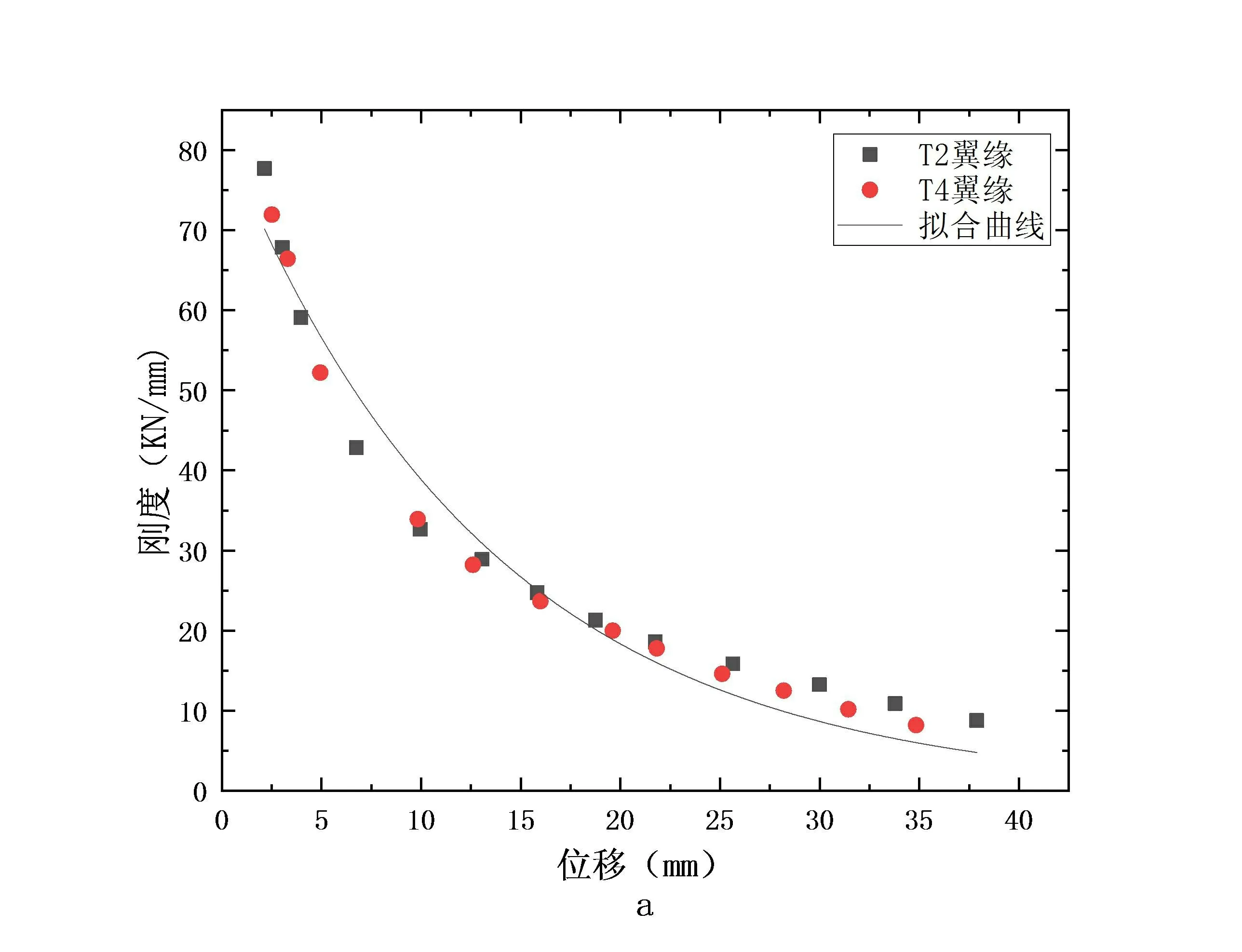
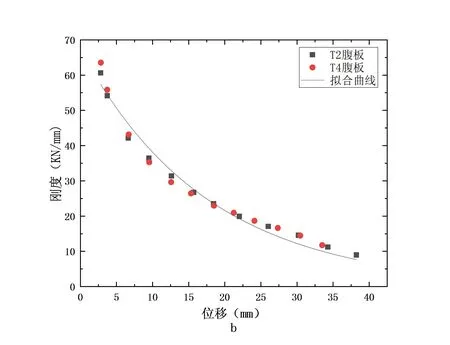
a-T2,T4翼缘;b-T2,T4腹板
由图1和图2可知,T型砌块整浇墙的刚度随着加载位移的增加而减小,前期退化速率大于后期速率,到达极限承载力后,刚度退化速率反而趋于平缓,说明T型墙体在后期依然具有较高的延性。
对比分析图1、图2和式(2)-式(5)可知,水平配筋的提高对构件的初始刚度及其退化速率影响不大,与文献[11-13]得出的结论一致。芯柱混凝土对于构件刚度和退化速率的影响较为明显,采用石墨尾矿混凝土作为灌芯材料的T2,T4较采用普通混凝土的T1,T3有着更高的初始刚度以及较快的衰减速率。
3 归一化刚度衰减方程
由图1、图2可以看出,不同墙体的刚度曲线离散性较大,为消除刚度离散性的影响,将各墙体的刚度归一化,采用两种方法:初始点刚度归一化及峰值点刚度归一化。
3.1 初始刚度归一化
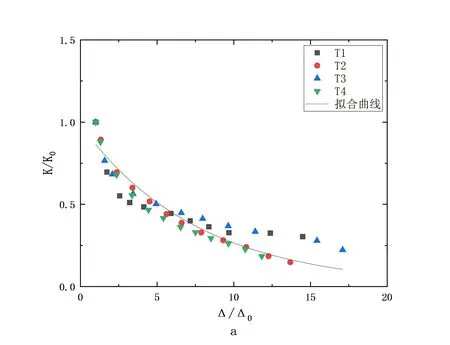
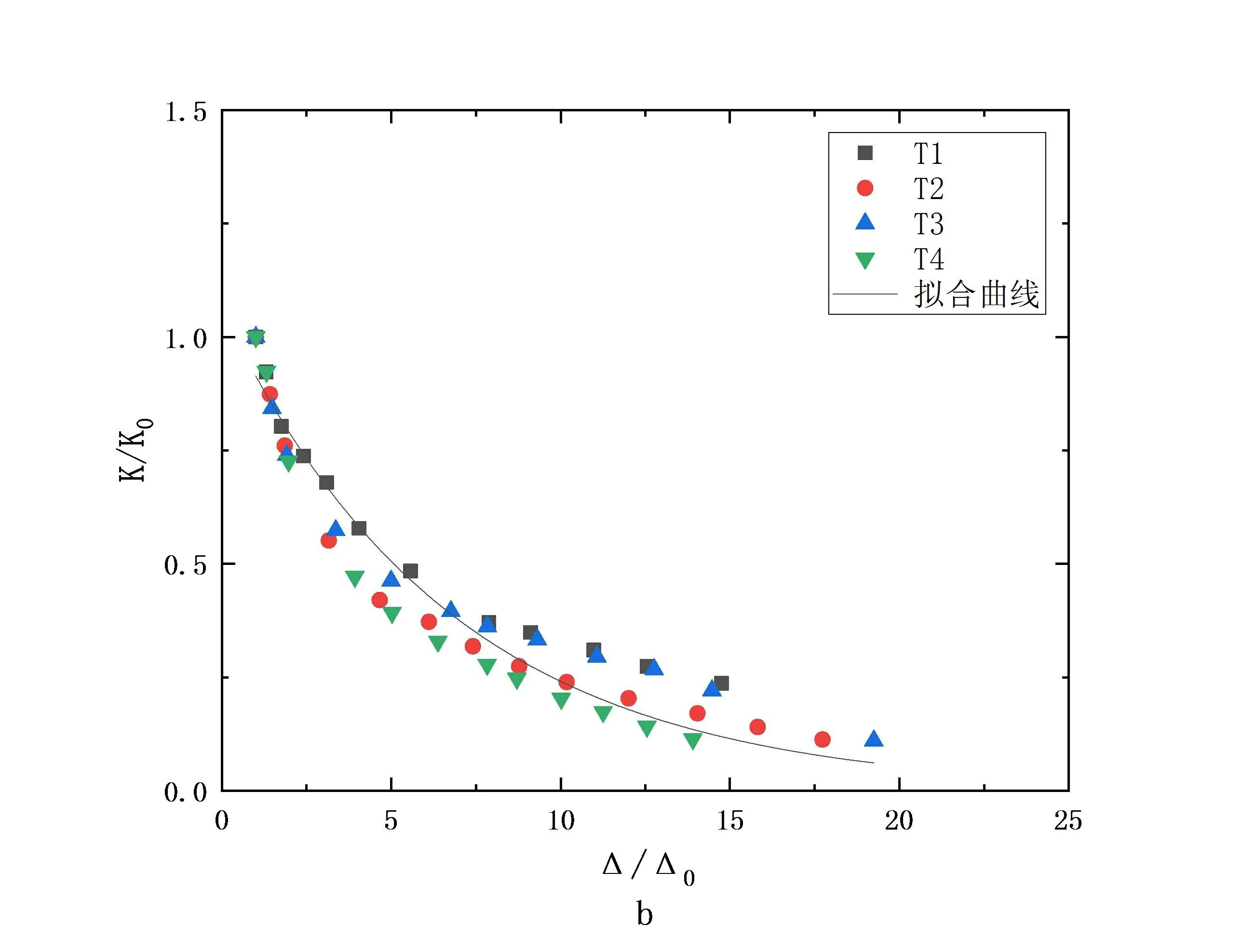
a-腹板;b-翼缘
将各墙体的刚度均除以初始刚度K0,将其定义为刚度退化系数ɑ0=K/K0,对应各点的位移均除以初始位移δ0=Δ/Δ0,得到α0曲线。将各墙体的ɑ0曲线进行回归,得到的回归曲线与试验值吻合较好,满足指数衰减规律,如图3所示。得到腹板的初始刚度归一化方程如式6所示:
K/K0=e(-0.13Δ/Δ0-0.01)
(6)
翼缘的初始刚度归一化方程如式7所示:
K/K0=e(-0.15Δ/Δ0+0.06)
(7)
其中:Δ为各点的位移值,Δ0为初始点位移值。
3.2 峰值点刚度归一化
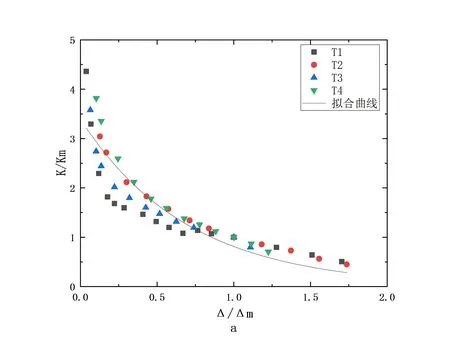
将各墙体的刚度均除以峰值点刚度Km,将其定义为刚度退化系数ɑm=K/Km,对应各点的位移均除以峰值点位移δm=Δ/Δm,得到αm曲线。将各墙体的ɑm曲线进行回归,得到的回归曲线与试验值吻合较好,满足指数衰减规律,如图4所示。得到腹板的峰值点刚度归一化方程如式8所示:
K/Km=e(-1.43Δ/Δm+1.22)
(8)
翼缘的峰值点刚度归一化方程如式9所示:
K/Km=e(-1.48Δ/Δm+1.35)
(9)
其中:Δ为各点的位移值,Δm为峰值点位移值。
对比式(6)和式7,式(8)和式(9),可以看出在两种表达曲线下,翼缘衰减速率更快,主要是在试验加载初期,腹板与翼缘相连的一端墙体所受到的荷载影响甚微,刚度基本不受影响,导致整体腹板墙体在加载过程中刚度退化速率低于翼缘。随着位移的增加,二者的α0、离散性更小,更加均匀,表明α0曲线更能准确表达墙体的归一化刚度衰减趋势。
4 结 论
利用4片砌块整浇墙低周往复荷载试验,研究了墙体在复合受力状态下的刚度衰减规律,得到了以下结论:
1)试验中由于灌芯材料的不同,墙体表现出不同的衰减规律。采用石墨尾矿混凝土作为灌芯材料的T2,T4较采用普通混凝土的T1,T3有着更高的初始刚度以及较快的衰减速率。水平钢筋的改变在本次实验中对初始刚度及刚度衰减没有体现出较大影响。
2)在位移较小时,同片墙体的翼缘衰减速度较腹板更快;当位移较大时,二者趋于一致。
3)通过对试验刚度的拟合得出刚度衰减方程及归一化刚度衰减方程,均满足指数衰减规律,拟合曲线与试验计算值吻合较好,此方程可以用于结构抗震计算分析的参考。
4)为消除各参数影响,得到统一的刚度方程,提出刚度退化系数的概念。计算分析表明,各次试验得到的α0-Δi/Δ0曲线比曲线αm-Δi/Δm更加均匀、稳定,离散性更小,建议采用α0曲线表示砌块整浇墙的刚度衰减更加合理。

