结合KPCA和XGBoost模型的企业经济危机风险预测研究①
贾 宁
(安徽绿海商务职业学院,安徽 合肥 230601)
0 引 言
在经济快速发展的今天,企业数量逐年增加,市场竞争也越来越激烈,企业面临的风险和财务危机也越来越多。为了避免或降低企业破产的危险,对企业进行财务经济危机预警是非常有必要的[1-2]。当前财务危机预警的相关研究成果较多,但很少考虑到财务预警指标变量间的相关性重叠问题,导致财务预警模型精度低,应用效果较差[3]。为此,研究利用核主成分分析(Kernel Principal Components Analysis,KPCA)和合成少数类(Synthetic Minority Oversampling Technique,SMOTE)过采样法对样本数据进行预处理,并将预处理的数据输入到XGBoost模型中进行财务危机预测。研究的主要创新点是利用KPCA来提取指标特征,以及利用SMOTE方法修正样本的平衡性。研究构建的模型具有较高的精度,能够为企业财务危机提供指导性的意见。
1 企业经济危机风险预测模型构建
1.1 财务预警指标体系构建及数据预处理
合理的财务预警指标体系,是实现企业财务经济危机风险预测的基础。研究以汽车行业为研究样本,基于既有的财务预警相关研究成果,从盈利能力、偿债能力、运营能力、发展能力、业务结构以及费用结构等6个维度选取指标,构建财务预警指标体系[4]。除了上述维度和指标以外,研究还将每股收益(Earning Per Share,EPS)作为一个关键指标纳入到财务预警指标体系当中。该指标只能针对上市公司,也是上市公司的核心指标,是上市公司估值的基础。基于上述内容,构建出财务预警指标体系,如表1所示。
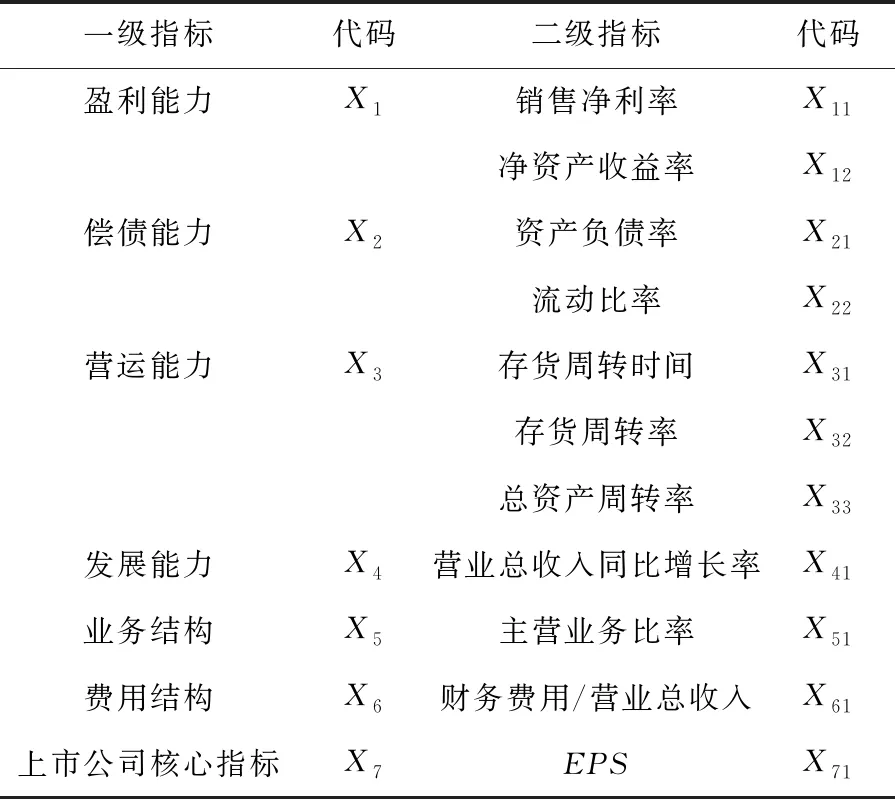
表1 财务预警指标体系
企业财务危机预警中,由于指标变量之间存在相关性重叠的问题,且财务数据的维度较高,导致企业财务预警模型的计算量大,计算过程复杂,且预测精度较低。针对这一问题,研究采用KPCA方法对数据进行降维处理。KPCA的基本思路为:对于数据集中一个样本数据{xi,i=1,2,…,n},将其进行升维处理,从而得到高维空间中的{φ(xi),i=1,2,…,n},在这个过程中,使原本变量间的非线性相关关系转换为线性相关,然后对数据进行降维处理。首先获取高维样本数据的协方差矩阵,对其进行特征分解,得到公式(1)。
φ(X)φ(X)Tωj=λjωj,j=1,2,…,d
(1)
在公式(1)中,φ(xi)表示维度为D*1(D≫d)的高维映射样本向量,λj表示C的特征值,ωj为λj对应的维度为D*1向量,φ(X)可表示为公式(2)。
φ(X)=(φ(x1),φ(x2),…,φ(xn))
(2)
ωj可以利用高维的样本向量来线性表示,如公式(3)所示。
ωj=φ(X)α
(3)
公式(4)中,α是n*1维的列向量。将公式(3)代入到公式(1)中,获得公式(4)。
Kα=λjα
(4)
利用公式(4)能够求解α=(α1,α2,…,αn),对于任意样本数据x,利用φ(x)在ωj方向上进行投影,即可获取到样本数据x在非线性降维后的xnew,实现样本数据的降维,如公式(5)。
(5)
除了样本数据特征降维以外,数据样本的平衡性也会影响到模型的预测精度。当不同种类的数据样本数量相差过于悬殊时,就会导致过拟合现象,降低准确精度。因此采用SMOTE算法对数据样本进行处理,修正数据样本的平衡性。SMOTE算法的原理是:在原样本数的基础上,随机重复采样并复制,从而使各个种类的样本数据数量达到平衡状态。基于上述内容,完成样本数据的预处理。
1.2 基于XGBoost的财务预警模型
XGBoost模型是近几年来开始兴起,并逐渐成为研究热点的一种大规模算法。其特点是能够在实现提升决策树(Gradient Boosting Decision Tree,GBDT)的基础上,实现部分广义线性机器学习算法。XGBoost模型可以利用CPU的多线程实现并行运算从而极大的提升了运算效率和预测精度。XGBoost模型能够支持多种基分类器,研究选用以树为基分类器的XGBoost模型进行财务危机预警。财务危机预警是一个分类问题,需要寻找一个合适的模型,并对模型不断优化求解,从而获得最佳参数。XGBoost模型是求解目标函数的最小值,来求解相应的模型参数。XGBoost模型的目标函数如公式(6)所示。
Obj(θ)=L(θ)+Ω(θ)
(6)
在式(6)中,θ是模型参数,L(θ)是损失函数,该指标主要用于评价模型在训练样本数据集中的拟合效果。但若只利用损失函数L(θ)来评估预测模型的性能,容易出现模型将噪声视为学习样本进行学习,进而导致过拟合的情况。因此在模型中加入正则项Ω(θ),以评估模型的复杂度。正则项优化可以降低模型的复杂度,进而提升模型的泛化能力。设XGBoost模型中集成树的数量为k,则基学习器产生的函数模型可表示为公式(7)。
(7)
公式(7)中,fk是一个基分类器,K为基分类器的数量,ρ是全部基分类器空间。此时,模型的目标函数如公式(8)所示。
(8)
公式(10)中,yi表示第i类类标记。XGBoost模型是一种表现形式比较特殊的提升树模型,其本质是一种加法模型。要求解模型的目标函数,就必须要获取每棵树的fk。但所有树的fk无法一次性获取,因此需要根据迭代了t-1次的模型进行训练,进而得到第t棵树。在迭代t次后,对模型的目标函数误差项,即模型的损失函数进行二阶泰勒展开,然后去掉常数项,并增加一个正则项,以对损失函数的下降进行约束,从而控制调整整个模型的复杂程度。基于上述内容,能够获取第t次迭代的目标函数,如公式(9)所示。
(9)
公式(9)中,gi和hi分别为XGBoost模型目标函数的一阶导数和二阶导数。一般来说,XGBoost模型的目标函数学习与损失函数的二阶导数直接相关。最小化目标函数后,就能够使模型达到最理想的分类效果,从而提升模型的精度。结合KPCA,SMOTE算法以及XGBoost模型,构建出企业经济危机风险预测模型,其流程如图1所示。
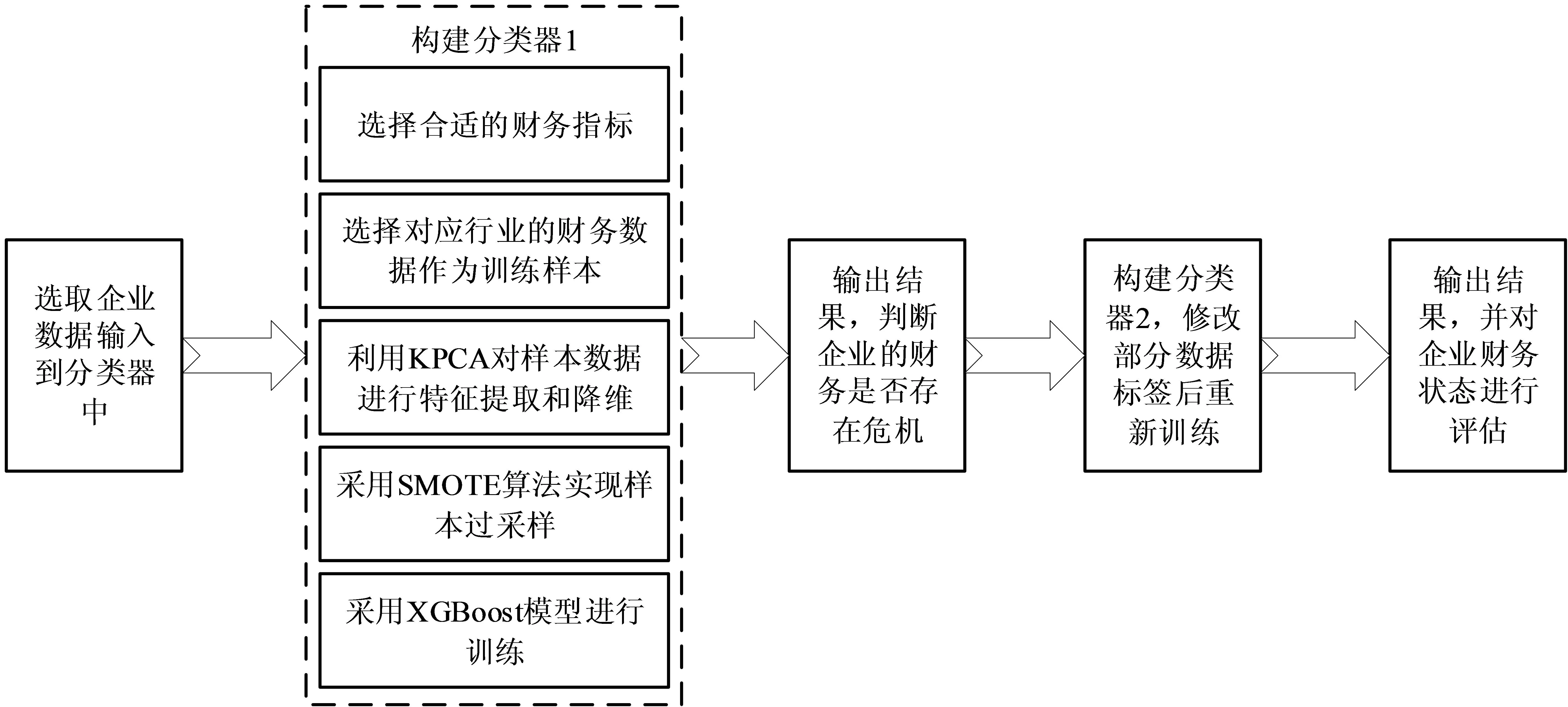
图1 企业经济危机风险预测模型的基本流程
在图1中,在分类器1内,若企业未出现财务危机,则输出结果为0;若已出现财务危机,则输出结果为2。在分类器2中,对未出现财务危机的企业进行预测,若企业可能发生财务危机,则输出结果为1,反之,则输出为0。
2 企业经济危机风险预测模型的性能分析
为验证研究基于结合KPCA,SMOTE算法以及XGBoost模型构建的企业经济危机风险预测模型的性能,研究选取了汽车制造行业的28家上市企业的财务数据进行研究。财务数据的年限为2011年~2021年,对原始样本数据进行预处理后,获取一个包含了3000条样本数据的实验数据集。将其中的70%作为训练样本数据集,对模型进行训练;其中的20%作为测试样本数据集,对模型的性能进行测试。分别构建研究结合KPCA,SMOTE算法以及XGBoost模型的企业经济危机风险预测模型(模型1)、KNN模型(模型2)、BPNN模型(模型3)以及决策树模型(模型4)等几种常见的财务危机预测模型。利用训练样本数据集对4种模型进行训练,训练过程如图2所示。
在图3中可以看到模型1在达到最佳精度时所需的迭代次数为45次,明显少于其他3种模型,且迭代至最佳精度后,误差为0.08,明显低于其他3种模型。利用测试样本数据集对4种模型的性能进行测试,测试结果如表2所示。
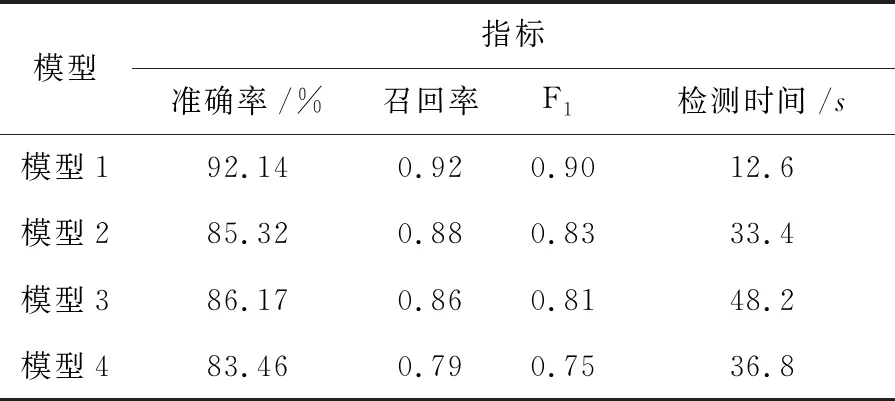
表2 4种模型的性能测试结果
在表2中可以看到,模型1的预测准确率达到92.14%,而模型2的预测准确率为85.32%,比模型1低6.82%;模型3的预测准确率为86.17%,比模型1低5.97%;模型4的预测准确率为83.46%,比模型1低8.68%。在4种模型中,模型1的召回率最高,为0.92,比模型2高0.04,比模型3高0.06,比模型4高0.13。在4种模型中,模型1的F1值最高,为0.90,比模型2高0.07,比模型3高0.09,比模型4高0.15。在4种模型中,模型1的所用的检测时间最少,为12.6s,比模型2少20.8s,比模型3少35.6s,比模型4少24.2s。利用接受者操作特性曲线(receiver operating characteristic curve,ROC)对4种模型的性能进行综合性的评估,如图3所示。ROC曲线下的面积AUC值越大,表示模型的性能越佳。
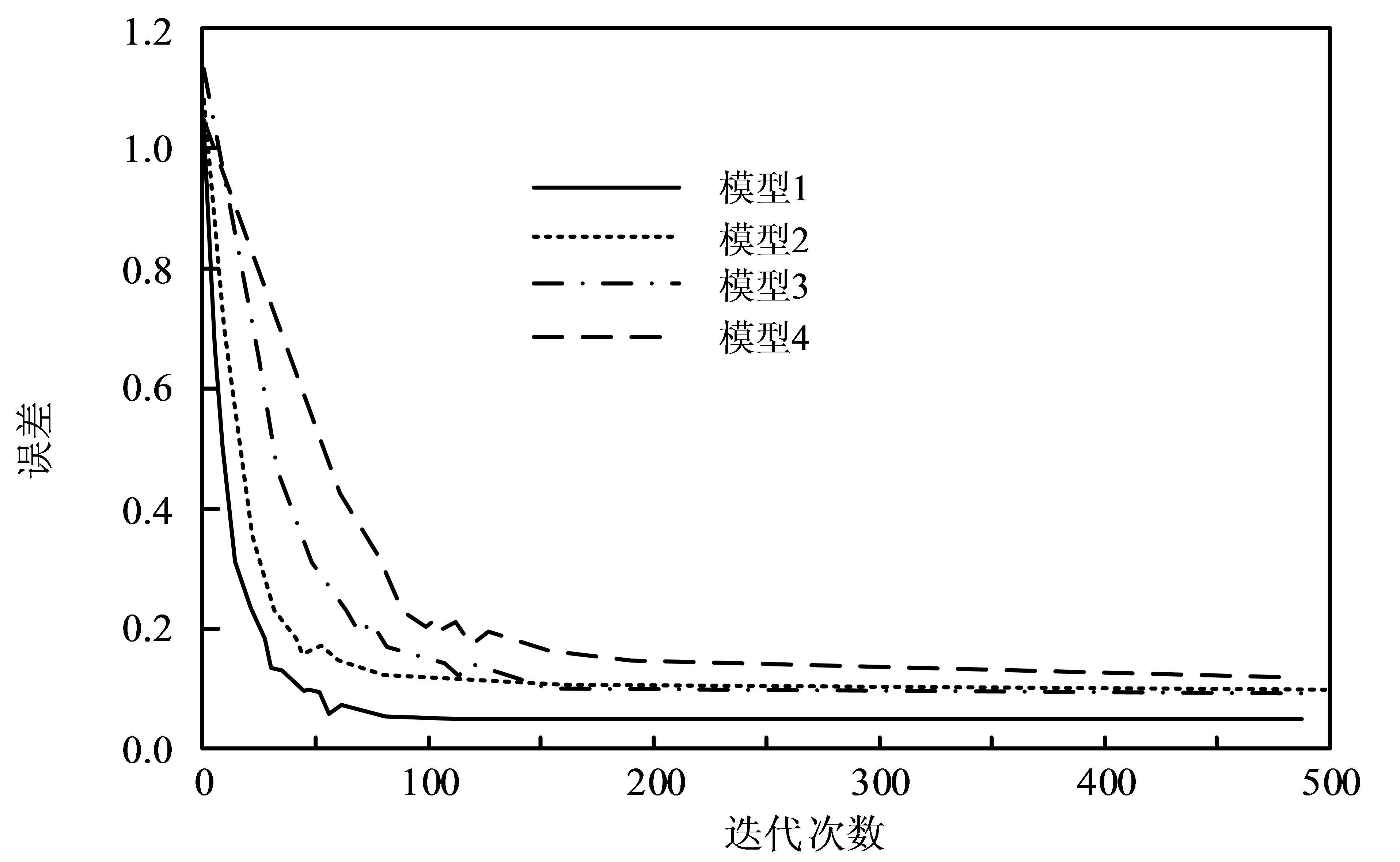
图2 4种模型的训练过程
在图3中可以看到,在4种模型当中,模型1的AUC值最大,显著超过其他3种模型。其中,模型1的AUC值为0.902,模型2的AUC值为0.863,比模型1的AUC值低0.039;模型3的AUC值为0.771,比模型1的AUC值低0.131;模型4的AUC值为0.694,比模型1的AUC值低0.208。综上所述,研究结合KPCA,SMOTE算法以及XGBoost模型构建的企业经济危机风险预测模型,其性能要明显优于几种传统的财务危机预测模型,因此具备较高的实用性,能够为企业财务管理提供准确、科学的数据支持。
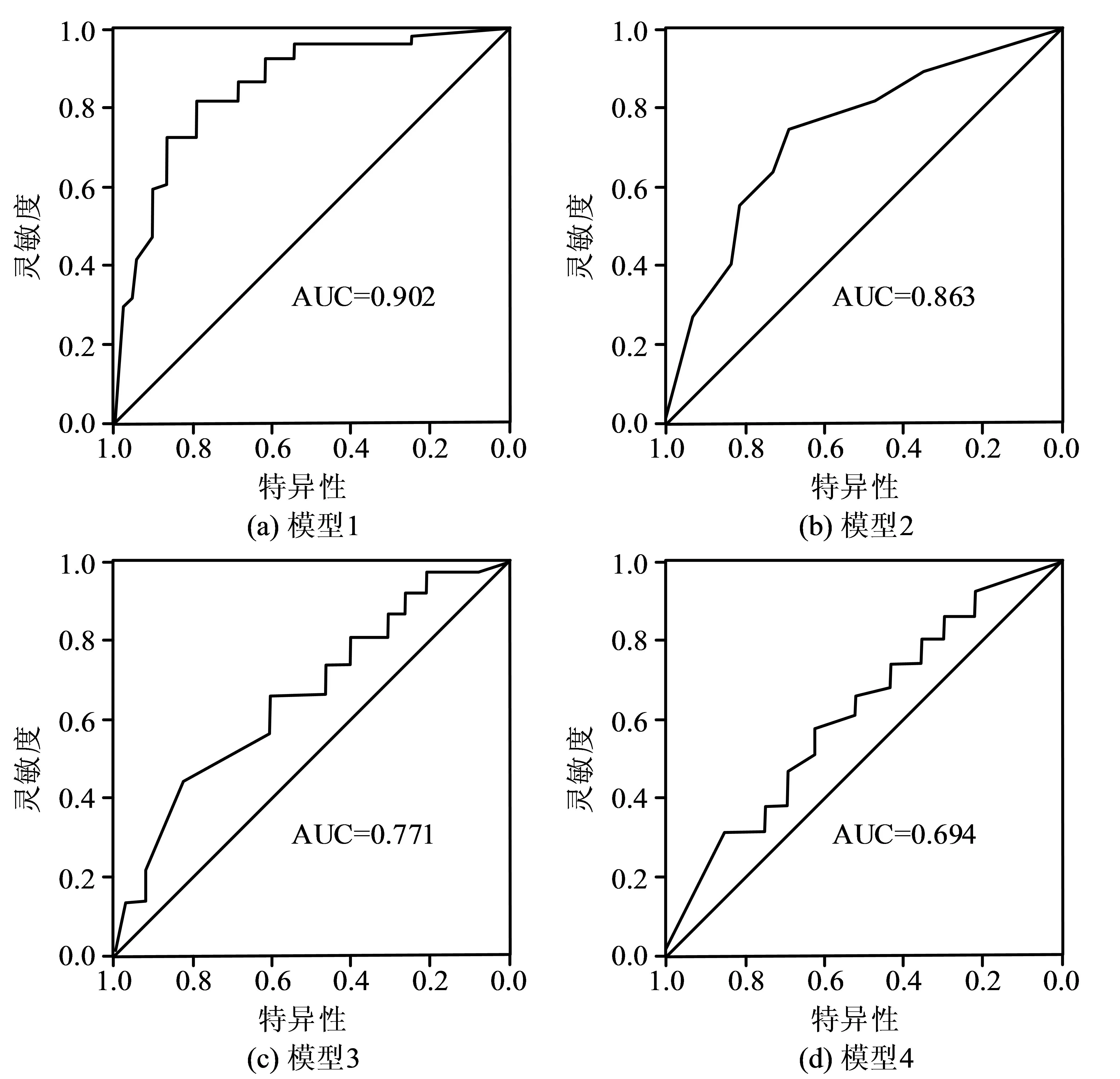
图3 4种模型的ROC曲线
3 结 论
对于各个企业而言,财务危机预警是必要的。研究结合KPCA,SMOTE算法以及XGBoost模型构建的企业经济危机风险预测模型,并利用28家上市企业的财务数据对模型性能进行了测试。测试结果显示,模型1在达到最佳精度时所需的迭代次数为45次,误差为0.08,均明显低于其他3种模型。模型1的预测准确率达到92.14%,召回率为0.92,F1值为0.90,均明显高于其他3种模型。模型1的AUC值达到0.902,比模型2高0.039;比模型3高0.131;比模型4高0.208。综上所述,研究提出的企业经济危机风险预测模型具有高精度、高效率的特点,对企业发展有着积极意义。

