AMPSO 与SVR 相结合的铣刀寿命预测研究
罗丹 , ,惠记庄 , ,丁凯 , ,张泽宇 , ,邵树军,杜超
(1. 长安大学 工程机械学院智能制造系统研究所,西安 710064;2. 长安大学 道路施工技术与装备教育部重点实验室,西安 710064;3. 陕西法士特齿轮有限责任公司,西安 710119)
智能制造作为新一代信息技术与制造技术融合发展的主攻方向,正推进生产过程智能化。车间智能化加工过程中,配置合理的数控刀具系统是保证工件加工精度和质量的关键。影响刀具系统稳定性与健壮性的关键一环为刀具寿命,若不能清晰确定刀具寿命影响因素以及合理的寿命预测方法,轻者影响工件加工质量,重者导致工件报废、机床故障,引起生产线迟缓[1]。因此,数控刀具寿命预测可作为切削参数配置和提前换刀的依据,准确的寿命预测可最大化刀具利用率,提高生产线加工效率,保证效益最优[2]。
国内外学者早期围绕数控刀具寿命计算方面开展了相关研究,主要使用Taylor[3]、Hasting 等[4]总结的刀具耐用度经验公式,但刀具加工过程复杂,当加工条件改变时,这些计算公式应用受限,无法满足新材料及高速铣削的要求。此外,生产实际中主要通过加工工件个数或走刀次数的累加来计算刀具使用寿命,但该方法存在准确度较差的问题。
为解决刀具寿命预测不准确问题,一方面,部分学者以BP 神经网络为主体智能算法引入刀具寿命预测问题中开展了相关研究。辛红敏与吴华伟[5]提出了用灰色系统理论预测盘铣开槽加工刀具寿命;Wu 等[6]介绍了一种基于随机森林的刀具磨损预测方法,并比较随机森林与前馈反向传播ANN 和支持向量回归机的性能;曾晓雪等[7]在粒子群算法的基础上引入混沌粒子更新位置,提出了基于CPSO-BP的刀具寿命预测方法,效果有所提升;李鑫等[8]通过对人工神经网络进行训练从而预测刀具磨损和切削力。
支持向量回归机[9](Support vector regression,SVR)基于统计学习发展而成,由于在小样本、非线性问题中具有优越的预测性能,部分学者将SVR 引入刀具寿命预测问题中亦开展了一定的研究。程灿等[10]建立基于支持向量机的刀具寿命预测模型,采用粒子滤波对回归结果进行修正,可准确识别刀具磨损量;Benkedjouh 等[11]基于非线性特征约简和支持向量回归建立了刀具剩余寿命预测模型,通过对刀具状态进行评估来预测其剩余使用寿命。
以上研究奠定了刀具寿命预测的基础,但是仍存在一定问题。神经网络在刀具寿命预测过程中存在收敛慢,不能在全局搜索得到最优结果的缺点。针对这一缺点,采用在小样本、非线性问题中预测性能较好的SVR 算法,但SVR 中的训练参数缺乏固定的选取准则,随机选取无法保证良好的预测效果。
考虑到粒子群算法(Particle swarm optimization,PSO)是一种搜索迅速、效率高、实现简单的群智能优化算法,部分学者在众多应用领域中引入PSO 优化。江鸿怀等[12]将PSO 引入五自由度机械臂轨迹规划问题中,结果表明经PSO 优化后,机械臂运动精度高。杨旭等[13]在信号去噪领域提出PSO 优化小波阈值函数中的未知参数,对滚动轴承振动信号进行自适应降噪处理。Deng 等[14]利用PSO 提高最小二乘SVM 的精度用于故障分类。
粒子群算法可提高解决工程应用的效率,但同时存在着过早收敛、搜索精度较低等劣势。本文在标准粒子群算法的基础上引入变异算子,形成自适应变异粒子群优化算法(Adaptive mutation particle swarm optimization, AMPSO),建立AMPSO 与SVR 结合(AMPSO-SVR)的铣刀寿命预测模型,对刀具寿命预测开展研究。
1 刀具寿命影响因素分析
当刀具几何参数、加工材料和铣削环境不变时,通常采用Taylor 经验公式[4]来评估刀具寿命,计算式为:
式中:T为刀具寿命;v为切削速度;f为进给量;ap为切削深度;n、C、C2、p、q、r为试验常数。
具体到铣削加工中,通过实践和经验总结出铣刀寿命计算式[15]为
式中:T为刀具使用寿命;Cr为 刀具寿命系数;D0为铣刀直径;v为铣削速度;ap为 铣削深度;f为进给量;aw为铣削宽度;Z为铣刀齿数;x、y、u、m、n均为影响指数。
由式(2)可知,v,f,ap为影响切削刀具寿命的主要因素;由式(3)可知,具体到铣削加工时,影响铣刀寿命的主要因素除了有v,f,ap之 外,还包括aw,D0,Z。由式(2)、式(3)可知,刀具寿命与上述因素呈高度非线性关系,且该非线性关系受加工环境的影响,所设置的试验常数和影响指数往往是在特定条件下经过多次加工试验拟合得到的。因此,采用传统的经验公式方法难以准确预测加工环境动态变化条件下的铣刀寿命。
2 寿命预测模型
根据上文中各影响因素与刀具寿命呈现非线性关系且难以采用经验公式直接解算,考虑到SVR 在处理非线性问题中具有优越的预测性能,因此通过训练SVR 模型构建各影响因素与铣刀寿命之间的关系。同时,针对SVR 模型参数难确定、参数设置不同对预测效果影响较大的问题,引入AMPSO 来寻找SVR 的最优参数,提高算法的预测精度。
2.1 支持向量回归机算法
对于数控铣刀寿命预测问题,给定训练样本数据集D={(xi,yi)},i=1,2,···,n, 其中:xi∈R6为影响铣刀寿命的6 个影响因素,yi∈R为铣刀实际寿命值。在SVR 模型中引入松弛变量来考虑允许拟合误差情况,经过非线性函数φ 将非线性问题转化到高维空间采用线性回归函数f(x)=wx+b进行回归,是结构风险最小化的近似实现。在此基础上,优化目标可转化为:
引入拉格朗日乘子,在Karush-Kuhn-Tucker(KKT)[16]条件下,得到对偶形式为:
进一步得到铣刀寿命预测函数为
针对铣刀寿命预测这一非线性问题,经过核函数K(xi,xj)将非线性问题映射到高维成为线性问题具有较强的预测能力。本文在多次试验的基础上选取了使预测误差最小的径向基函数作为SVR 的核函数。
2.2 自适应变异粒子群优化支持向量回归机算法
标准的粒子群算法假设在一个 D维的搜索空间中,有n个粒子组成的种群X=(X1,X2,···,Xn),其中第i个粒子的速度Vi=[Vi1,Vi2,···,ViD]T,个体极值Pi=[Pi1,Pi2,···,PiD]T,种群的全局极值Pg=[Pg1,Pg2,···,PgD]T。粒子的速度和位置更新方式如下:
式中: ω为惯性因子;d=1,2,···,D;i=1,2,···,n;k为当前迭代次数;Vid为粒子的速度;c1和c2为加速度因子;r1和r2为区间[0,1]上的随机数。
为了设置较优的SVR 模型的参数组合c和 σ,同时改善标准的粒子群算法,本文在PSO 算法的基础上引入自适应变异算子,构建AMPSO 算法来优化SVR 模型的参数组合c和 σ。该改进算法的基本思想是:在每次粒子更新后,以预先设定的概率对粒子设置初始化操作,使粒子在更大的空间展开搜索,增加新解的可能性,使其跳出目前局部最优解,提高模型搜索到SVR 参数最优值的可能性。AMPSO 算法中的粒子更新过程如下:
经过k次迭代,第i个 粒子在 D维搜索空间的位置为 pop(j,k),p为变异阈值,当粒子满足大于阈值时,将跳出当前位置,出现新的位置,否则保持不变,即:
式中:p为0 ~ 1 之间的常数;c eil(x)将x四舍五入为大于或等于最接近x的 整数, sizepop为种群最大数量;popgmax、popgmin分别为SVR 核函数参数变化的最大值和最小值。
2.3 铣刀寿命预测步骤
通过对支持向量回归机算法和改进粒子群优化算法的介绍,构建基于AMPSO-SVR 的铣刀寿命预测模型。首先用AMPSO 对SVR 的惩罚参数和核函数参数进行全局寻优,基于得到的最优参数值训练SVR 算法,从而可以更好地提升预测效果,模型的具体实现步骤如下:
1)在分析铣刀寿命影响因素的基础上,确定预测模型的输入为铣削速度、每齿进给量、铣削深度、铣削宽度、铣刀直径和铣刀齿数,输出为铣刀寿命;
2)初始化AMPSO 参数,其中种群迭代次数为200,种群数量为20;
3)将SVR 中的参数c和 σ作为AMPSO 算法的粒子种群位置进行随机初始化,归一化后的训练样本数据作为AMPSO 算法的输入,将铣刀实际寿命与预测寿命之间的偏差转换为AMPSO 算法的适应度函数值,适应度函数fitness(记为Ffitness)为预测误差平方和的倒数,即其中,f(xi)、yi分别为第i个训练样本数据的实际寿命和预测寿命,n为输入样本数据的总数;
4)将每个粒子的当前位置作为目前最优解,计算各自适应度值,根据式(7)和式(8)更新每个粒子的速度和位置;
5)根据式(9)和式(10)进行粒子自适应变异操作;
6)判断每个粒子的适应度值是否满足误差要求,若满足,则得到最优的参数组合;若不满足,则返回步骤4)继续迭代;
7)基于所得的最佳参数c和 σ组合,以训练样本数据作为输入,将寻优得到的参数值赋给SVR 进行训练,得到基于AMPSO-SVR 的铣刀寿命预测模型。选用作为SVR 模型的核函数, σ为高斯核函数参数;
8)输入测试样本数据进行预测,反归一化输出最终预测结果,通过计算实际寿命与预测寿命之间的偏差,来检验所建立的铣刀寿命预测模型的预测准确率。
3 案例研究
3.1 数据来源
本文选取文献[17]的铣削实验数据验证所提出模型的有效性。该实验采用的铣刀材料为硬质合金钢,在要求粗铣加工的情况下,采用立铣加工方式,加工材料为45 钢的工件,实验数据如表1 所示。本文以前第1 ~ 7 组数据为训练样本数据集,第8 ~ 10 组数据为测试样本数据集。

表1 实验样本数据(训练 + 测试)
3.2 AMPSO 与SVR 相结合的预测实例分析
首先,将表1 中的第2~7 列作为模型的输入,最后一列作为模型的输出,训练并测试基于AMPSO-SVR的铣刀寿命预测模型。将训练样本集(编号1~7)的输入数据归一化后,采用AMPSO 算法得到优化后SVR 中的参数:c=12.94,σ =0.01。
其次,采用SVR 训练得出铣刀寿命预测模型,计算该模型在训练集上的预测结果如图1 所示,图中标出了针对每个训练样本的铣刀寿命预测相对误差,最小为0.350 46%,最大为1.349 60%。因此,所训练的基于AMPSO-SVR 的铣刀寿命预测模型在训练样本集上可较准确地预测铣刀寿命。
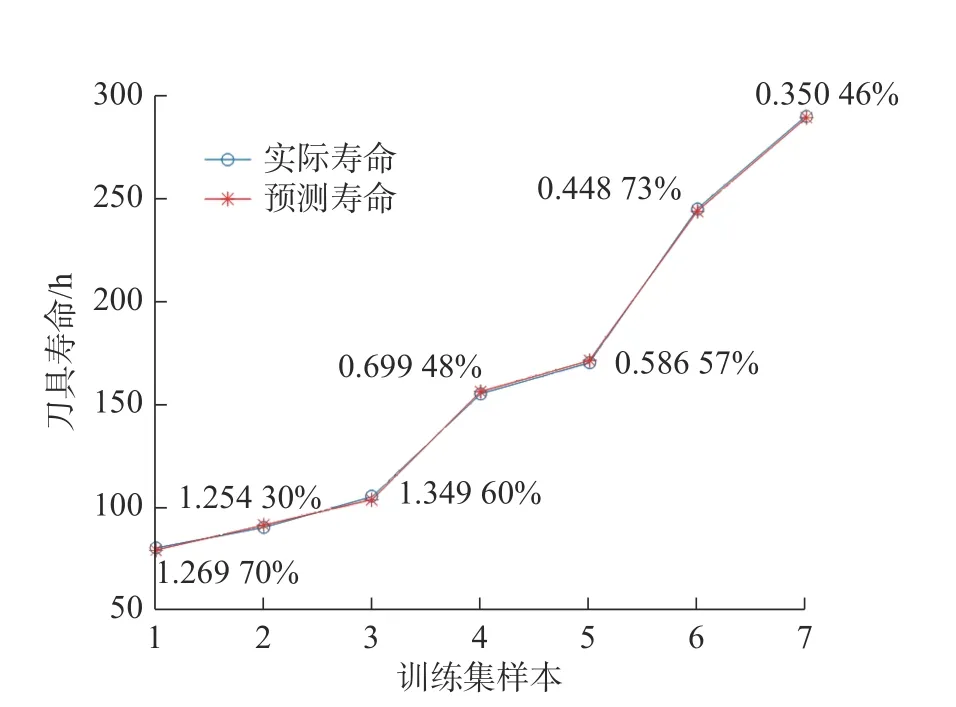
图1 训练样本集上的铣刀寿命预测结果
最后,在测试样本集(编号8 ~ 10)上对所训练的AMPSO-SVR 模型进行验证,得到的铣刀寿命预测结果如表2 所示。由表2 可知:预测寿命与实际寿命之间的相对误差最小为0.587 2%,最大为0.908 8%。因此,所训练的基于AMPSO-SVR 的铣刀寿命预测模型在测试样本集上也可较准确地预测铣刀寿命。

表2 测试样本集上的铣刀寿命预测结果
进一步地,本文采用平均平方误差 M SE和平方相关系数r2这两个指标来评价预测结果准确性。MSE是对预测寿命与实际寿命之间的偏差度量,其数值越小说明预测模型具有更好的精确度;r2取值范围在[0,1]内,其值越接近1,表明模型的性能越好。本文所建立的AMPSO-SVR 模型在测试集上的MSE为1.156 48×10-4,r2=99.917 7%,表明模型预测性能较好。
由以上计算结果可知,本文所提出的基于AMPSO-SVR 的铣刀寿命预测模型在训练集和测试集上的预测准确度高且误差小,可以较准确预测该型号数控铣刀的使用寿命。
3.3 预测结果对比分析
3.3.1 数据预处理方式对比
原始数据预处理时,是否归一化以及不同的归一化方法对预测准确率也会产生一定影响,表3 分别给出了不归一化、归一化至[-1, 1]和归一化至[0, 1]这3 种情况下的相对预测误差结果对比。

表3 归一化方式对比
由表3 可知,本文将原始数据归一化至[-1, 1]时,其预测误差小于不归一化和归一化至[0, 1]这两种方式。因此,将原始数据归一化至[-1, 1]之后输入AMPSO-SVR 模型进行铣刀寿命预测,能够获得更高的预测精度。3.3.2 SVR 参数优化算法对比
SVR 中的惩罚参数c和核函数参数 σ对寿命预测结果影响很大,常用网格搜索(Grid search,GS)等方法进行参数的选择。网络搜索时设置参数c和σ都 为2-10,2-9,···,210。针对测试数据集,将GS-SVR、BP 神经网络和本文所提出的AMPSO-SVR 算法的预测结果进行比较,如表4 所示。

表4 算法预测结果对比
通过对比可知在上述参数设置下,GS-SVR 查找速度较快,但是精度不及AMPSO-SVR。采用AMPSO-SVR 的训练时间比BP 神经网络的训练时间短,模型的训练效率较高,且能够得到更小的误差和更高的预测精度。
4 结论
1)以数控铣削加工为例,采用AMPSO-SVR 算法对铣刀寿命进行预测时,相较于原始数据不归一化和归一化至[0,1],将原始数据进行[-1,1]归一化处理后,预测精度更高。
2)相较于网格搜索法、BP 神经网络等算法,采用AMPSO-SVR 算法对铣刀寿命进行预测的预测误差小、精度高、泛化能力强;同时,相较于BP 神经网络算法,AMPSO-SVR 算法的训练时间短、效率高。
3)本文所提出的基于AMPSO-SVR 的铣刀寿命预测模型可以为车间刀具准备和换刀决策提供依据。
4)后续将在获取大量铣刀切削样本数据的前提下,开展大数据驱动的铣刀寿命预测研究。

