遗传算法优化的非线性悬架系统仿真研究
刘涛,张勇
(1. 烟台南山学院 智能科学与工程学院,山东烟台 265713;2. 河南省计量科学研究院,郑州 450008)
路面不平度、车辆速度及悬架系统性能会影响汽车振动情况,汽车振动会严重影响汽车平顺性和操纵稳定性等性能[1]。平顺性是衡量汽车舒适性的重要指标之一,汽车平顺性可以用车身振动加速度来评价[2]。
路面状况、汽车速度硬性条件下,悬架系统振动性能优良可有效改善汽车平顺性。目前普通轿车多采用线性被动悬架系统,线性被动悬架有性能可靠、结构简单、成本低等优点[3]。此种悬架只能对固有频率段减振效果明显,如何设计悬架结构、调整参数来改善汽车平顺性是被动悬架参数优化设计的关键问题。
Gourdon 等[4]指出非线性悬架具有优越的宽频减振特性,并能提高减振效率。非线性悬架的振动抑制机理是靶能量传递(Targeted energy transfer,TET),TET 在振动抑制中应用非常广泛[5]。文献[6]研究了外界激励下,非线性悬架不同的参数对悬臂梁结构振动抑制效果的影响;文献[7]证明了非线性减振器可有效吸收结构振动。研究表明,在设计得当的前提下,非线性悬架具有良好的减振效果。
本文提出一种非线性悬架的设计方法,利用普通线性弹簧的空间组合构建Duffing 振子;建立含立方刚度的二自由度非线性悬架系统的动力学模型,利用增维精细积分法求解非线性悬架的数学模型,利用遗传算法找出某段速度范围内,悬架的最优参数,通过Simulink 对比仿真,确定非线性悬架的优越性,通过运算仿真表明,所构建的非线性悬架系统具有良好的宽频特性,并取得明显的减振效果。
1 非线性减振悬架系统
1.1 动力学模型
将整车系统的1/4 简化成一个汽车振动模型,需要做如下假设[8-9]:
1)总质量不变,质心位置不变,转动惯量不变;
2)悬挂质量分配系数为1,汽车前、后悬架振动彼此没有联系,不考虑车身的俯仰、前后轴的垂向跳动;
3)车辆几何尺寸和质量近似认为左右对称;
4)在低频路面激励下,车辆的左右两个车轮轨迹输入具有较高的相关性,认为左右两侧以完全相同的方式运动。在高频路面激励下,认为激励只涉及到车轮跳动,对车身运动影响甚微,车身左右两边的相对运动就可忽略。
利用两个普通的线性弹簧空间组合构建Duffing振子,建立如图1 所示的二自由度非线性悬架系统。其中,非簧载质量为m1, 簧载质量为m2,轮胎刚度为k1, 悬架弹簧刚度为k2,悬架阻尼系数为c,非簧载质量位移为x1, 簧载质量位移为x2,路面不平度函数为q,弹簧自由长度l。

图1 二自由度非线性悬架系统
根据牛顿运动定律,非线性悬架系统强迫振动的微分方程为:
令:
则动力方程可化为
1.2 数学模型求解
非线性悬架构成的非线性力学系统是复杂的,求多自由度非线性振动的高精度解是困难的,精细积分法[10-13]在求解线性定常振动方程时,可得到较高精度的解。利用增维精细积分法化非线性动力方程为形式上的齐次方程再求解,使高精度的计算多自由度非线性方程得以实现。
利用增维精细积分法求上述方程,令x2=y,x˙2=y1,x1=z,x˙1=z1,x5≡1 ,可转化为
其中:
式(3)在形式上已化为线性非齐次方程,记时间步长τ,在很小的时间间隙内,则可以用精细积分法,式中通解为齐次解vh与特解vp之和,即
在t∈[tk,tk+1]积分区间内,齐次解为
式中: [T(τ)]=exp(Hτ), τ=t-tk;{c}为由初始状态tk决定的积分常向量。假定特解已求出,可以求出{c}=v(tk)-vp(tk),则
令t=tk+1,可得到积分公式为
当积分区间足够小时,认为外载是线性变化的,可采用线性插值的方法求解,r(t)=rk+r1(t-tk),rk是在该步内给定的向量,
则相应的解为
T(τ)利用指数函数的加法定理,则
式中:m为任意正整数,m=2N;由于τ 是一个很小的时间区段。则η =τ/m是 一个非常小的时间区段,对于η,有可写为:
式中Ta为 一个小量矩阵,当它与单位阵In相加时,去前四项的结果即可满足要求。
为了计算T有
由式(12)相当于执行语句
当循环结构结束时,有
式(14)构成了T(τ)计算表达式,可得到高精度解。
为提高精度,当计算出v(tk+1)后,对H进行修正,则
将修正后的H重新代入式(9)知道满足下列条件
式中: ε为设定的阈值;j为迭代次数。当式(16)成立时,认为v(tk+1)是所求解。
1.3 路面激励模型
路面粗糙程度的不同决定了路面等级不同,路面粗糙程度可用路面不平度系数G0表示,根据不同路面粗糙程度建立含有速度参数的积分白噪声路面激励模型时域模型。
式中:u为汽车车速;w为单位强度为1 的随机白噪声。
2 非线性悬架优化模型
2.1 设计变量
在汽车其他参数一定下,根据建立的非线性悬架,在悬架参数设计可行域内,选取合适的弹簧刚度和阻尼器阻尼,使得悬架系统的减振性能最优。将非线性悬架的弹簧刚度和阻尼系数作为优化设计变量,即
2.2 约束条件
为保证设计悬架的合理性,需要添加所设计参数的约束条件,使悬架系统性能指标符合设计要求,本优化模型的约束条件包括偏频和阻尼系数的取值范围。
汽车偏频的取值对汽车行驶平顺性影响较大。一般推荐偏频的取值范围如表1 所示;阻尼系数的范围受到减振器设计参数的影响。

表1 轿车偏频取值范围[14]
2.3 目标函数
路面输入模型采用白噪声型式,垂直轴向频率加权函数的频率范围广,已失去讨论意义。用加权峰值系数表征汽车平顺性,当加权峰值系数<9 时,可直接用车身总加权加速度均方根值来评价振动对人体舒适性和健康的影响。本文以车身总加权加速度均方根值最小值作为优化目标函数。
式中:awu(t)为某一车速下加权加速度时间历程;awu为某一车速下加权加速度方均根值。
某一汽车行驶周期内车身总加权加速度方均根值aw,可表示为不同车速下加权加速度方均根值awu与 此车速所占时间比例fn的和。
式中f1+f2+···+fn=1。
综上,可表示为在线性悬架的弹簧刚度和阻尼系数限制条件下,找到合适的弹簧刚度和阻尼系数,使得总加权加速度均方根值最小。即:
式中:k2′、k2′′为 弹簧刚度的上下限;c′、c′′为阻尼系数的上下限。
2.4 遗传算法仿真分析
遗传算法是一种全局优化概率搜索算法,因其操作简单、适用性广、鲁棒性强等优点而被广泛应用。其基本原理仿效生物界中的“物竞天择、适者生存”的演化法则。通过把问题编码为染色体,选择合适的适应度函数,先产生初始种群,仿照自然界的淘汰机制对个体进行选择、交叉和变异等操作。最终生成符合优化目标的染色体,再进行反编码得到最优解[15-17]。
本次设计建立如图2 所示算法分析路线,计算目标函数时,调用1/4 车辆模型控制方程,遗传算法程序进行选择、交叉和变异操作,求得最优解。
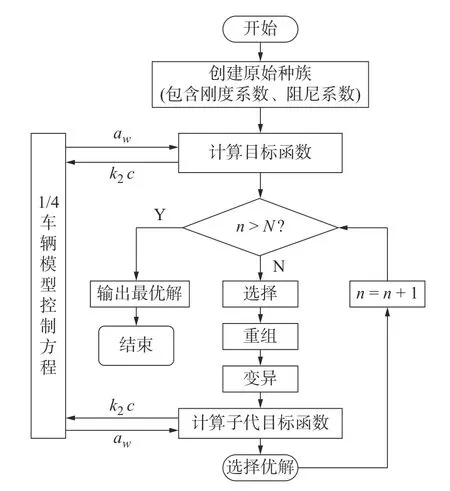
图2 遗传算法仿真路线
3 案例分析
3.1 算法仿真
以某轿车参数为例,车辆模型参数如表2 所示,遗传算法程序中:种群大小为40,遗传代数为200,代沟为0.95,交叉概率为0.7,变异概率为0.01,15 000≤k2≤25 000 N/m, 1 000 ≤c≤2 000 N·s/m,1 ≤u≤20m/s,取l= 0.3 m,并假设不同车速所占时间比列相同,按所述方法进行仿真。

表2 车辆模型参数
如图3 所示,遗传代数增加到30 代左右后,解不再发生变化,此时所求的解为最优,最优解为k2=19 482.3,c=1 235.3,aw=0.73。图4 为在此总体最优条件下,不同车速awu的变化,可见总体而言awu数值较小,变化较小,可认为取得了较为良好的减振效果,当车速为16 m/s 时,awu数值较大,针对这一数据引入Simulink 仿真,进一步分析、评估此时的减振效果。
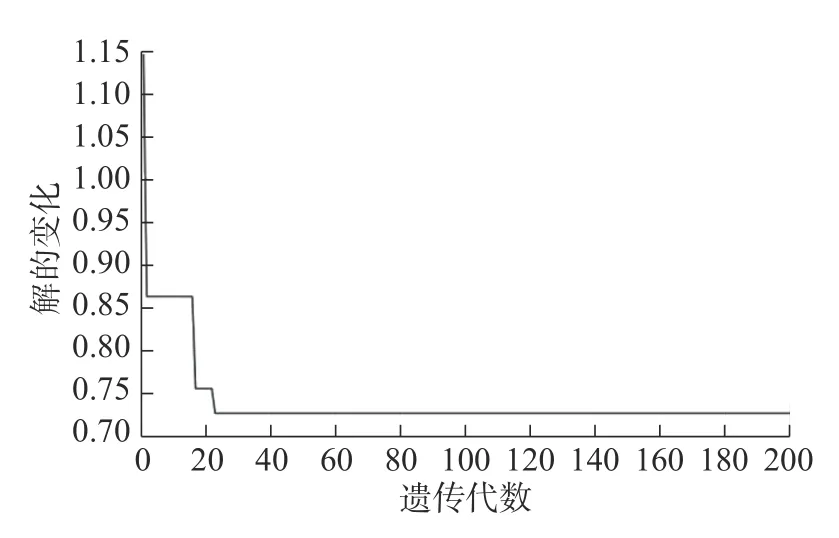
图3 遗传代数及解的变化曲线

图4 不同车速下加速度方均根值
3.2 Simulink 仿真分析
在Simulink 中建立如图5 所示的非线性悬架仿真模型,路面激励模型选用车速为16 m/s 时的时域输入模型,线性悬架仿真模型可参考文献[10]中的模型建立方法,设定已知参数和计算出的参数,设定仿真时间为10 s,进行仿真。
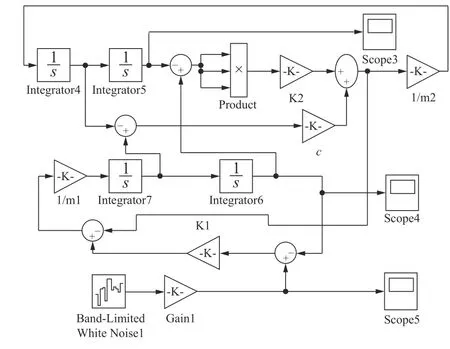
图5 Simulink 仿真模型
图6为路面时域输入模型。线性悬架车身与非线性悬架车身位移如图7、图8 所示。图7 可看出,普通线性悬架减振效果已比较优秀,对比图7、图8可发现,在车速为16 m/s 时,awu数值较大条件下,非线性悬架系统减振效果要好于普通线性悬架。

图6 路面不平度输入模型

图7 线性悬架车身位移
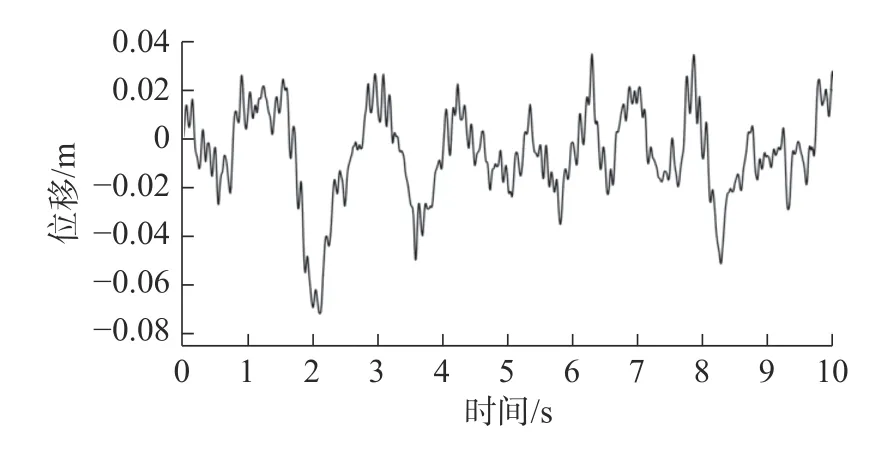
图8 非线性悬架车身位移
4 结论
1)本文通过利用线性减振弹簧空间的改变,提出一种切实可行的非线性悬架减振系统构建方法。
2)构建1/4 汽车的非线性悬架减振系统动力学模型,利用增维精细积分法得到非线性悬架动力学模型的高精度解。
3)以车身总加权加速度均方根值最小值作为优化目标函数,利用遗传算法求解限制条件下,非线性悬架系统的弹簧刚度和阻尼系数,并利用Simulink仿真,对比非线性悬架与线性悬架,进一步确定所建立非线性悬架系统的可行性和优越性。
4)路面激励模型时域模型采用积分白噪声,使得计算结果存在较小出入,应继续对此讨论研究。

