让学生在复习中学会复习

摘 要 小学数学教学中，如何在单元整理和复习中以生为本提升学生复习力？结合“长方体、正方体的整理和复习”教学实践，总结提升学生复习力的教学策略：课前知识梳理、课中思维碰撞、课后方法提炼，教师引领学生在知识梳理、绘图分析、易错辨析、困惑解析、方法提炼等数学活动中感悟数学思想方法，学生亲历复习课的“浑然”“泰然”与“豁然”过程，在复习中提升复习力。

关键词 小学数学 复习力提升 教学策略

小学数学复习课是对某一阶段所学数学知识进行的归纳整理、查漏补缺，它不是简单的知识巩固过程，而是引导学生自主整理、建立知识网络的过程，是不断完善学生认知结构，使之条理化、系统化的课堂教学模式。加强数学学生复习力提升策略的实践研究，对提升数学教师专业素养、发展学生核心素养具有重要的现实意义。在实际复习课教学中，复习课教学存在“三课三缺”现象：课前再现受阻——缺少知识梳理、课中单向输入——缺乏思维碰撞、课后机械训练——缺失方法提升。小学数学复习课教学，尤其是以提升学生复习力为目标的复习课教学，需要教师在实践中边探索边总结。结合笔者在“长方体、正方体的整理和复习”中的教学实践与思考，阐述提升学生复习力的教学策略，旨在让学生在复习中学会复习。

一、课前引导知识梳理和自我检测

长方体和正方体是最基本的立体图形，是学生从二维空间转向三维空间学习的起始，是进一步学习其他立体图形的基础，长方体和正方体体积的计算也是形成体积概念、掌握体积计量单位和计算各种几何形体体积的基础。为了更精准地把握学情，教师设计课前任务单，提前一天让学生自主整理和复习[1]。教师可以设计复习课任务单，任务单内容可以分成三部分：

（1）本单元你有哪些收获？根据自己的理解画出思维导图。

（2）推荐一道本单元的易错题，并尝试解答。

（3）关于本单元，你还有什么疑惑吗？写下来，老师会帮你。

课前，学生自主整理知识并尝试形成思维导图，在摸索中前行，初步学会复习，为复习课上的交流分享奠定坚实的基础。教师通过分析任务单上学生的作答，探明学情，为有效地复习做好铺垫。

二、课中思维碰撞和进阶

课中围绕课前任务单的三个问题展开教学活动，所有的学习内容均来自学生自己收集并上交的内容。教师对学生绘制的思维导图进一步梳理知识结构，对学生摘录的易错题进行思辨，在学生提出的困惑中有针对性地解疑释惑，学生在一个又一个问题解决的过程中不断碰撞出思维火花，获得思维的逐级进阶，逐步学会复习。

（一）浑然——于知识梳理中学会融会贯通

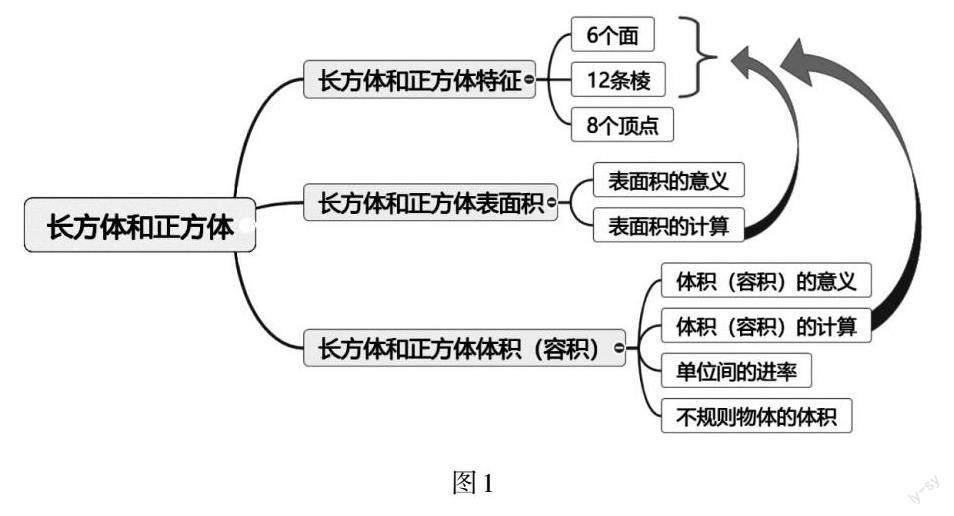
1.绘制思维导图整理知识点。长方体和正方体单元内容的编排分为三小节：长方体和正方体的认识、长方体和正方体的表面积、长方体和正方体的体积，在长方体和正方体的体积这一节中，还介绍了容积的概念，并探索某些实物体积的测量方法。为此，在点评学生们的思维导图作品后，教师要借助课件引导学生以关键词“特征”“表面积”“体积（容积）”作为第一级标題绘制单元思维导图。长方体和正方体的特征主要从棱、面、顶点三个方面进行研究，长方体、正方体的表面积和体积（容积）主要从定义和计算两方面进行研究，把这些关键知识点作为第二级子标题。单元思维导图二级子标题之间又紧密相连，其中长方体、正方体表面积和体积的计算离不开对棱和面的学习，借助箭头进一步完善思维导图。至此，简约的思维导图形成（如图1），学生逐步感受到整理就是一个由厚到薄的学习过程。

2.发现并提出生活中的数学问题学会融会贯通。教师可以引导学生发现实际生活中存在的有关长方体和正方体的知识，并将知识梳理以问题的形式呈现，学生在发现问题、提出问题、分析问题、解决问题中学会融会贯通，实现知识与素养、数学与生活浑然一体。例如，教师可以出示一个鱼缸图，鱼缸的棱是用角钢做成、四周用玻璃做成、底面用铁板做成，让学生发散思维提出与本单元相关的数学问题。开放性的问题激活学生的思维，学生提出如下数学问题：“做这个鱼缸要用多少分米的角钢？做这个鱼缸要用多少平方分米的铁皮？做这个鱼缸要用多少平方分米的玻璃？这个鱼缸占多少空间？这个鱼缸装多少升水？”等。每一个问题都指向本单元的知识，求长方体的棱长总和、底面积、侧面积、体积、容积等，围绕鱼缸将本单元知识串成线、结成网[2]。

（二）泰然——于易错辨析中学会举一反三

学生在课前自主整理和复习阶段时摘录了许多易错题，教师在备课时需要分析学生的易错题，并从中选取具有普遍性、探究性的错题，引导学生进行辨析，并引申出与之相关的数学问题，由一道题触及一类题，在对比深化中学会举一反三，这样的思维习惯有助于学生在面临更难的挑战时也能泰然自若。

例1，有学生摘录易错题“王师傅在一个棱长8厘米的正方体木块顶点上挖下一个棱长2厘米的小正方体，剩下部分表面积可能是多少平方厘米？”。解答：“8 × 8 × 6 - 2 × 2 × 2 = 392（厘米）”。

从学生的作答中可以看出这果然是一道易错题，以至于学生在摘录错题时依然保留原来的错误作答，无法改正过来。教师如果没有在课中引导辨析，学生自己都不知道错在哪里。为此，教师将以上错题呈现在课件中，让学生思考辨析“这样写对吗？请说明理由。”

生1：8 × 8 × 6算的是原来正方体的表面积没错，但2 × 2 × 2是体积，两个算式的意义不同，不能相减。

生2：挖下一个棱长2厘米的小正方体，体积是减少了，但这里要求的是表面积，正确列式是8 × 8 × 6 - 2 × 2 × 6。

生3：我不同意生2的列式，体积减少表面积不一定减少，通过平移的方法（边说边在图上做标记）可知表面积不变，所以剩下部分的表面积应该是8 × 8 × 6 = 384（平方厘米）。    其余同学响起热烈掌声！

生4：这里计算错误，正确的列式要注意计算正确哦。

生5：表面积的单位应该是平方厘米，不是厘米。

……

师：你还能想到其他类似的数学问题吗？

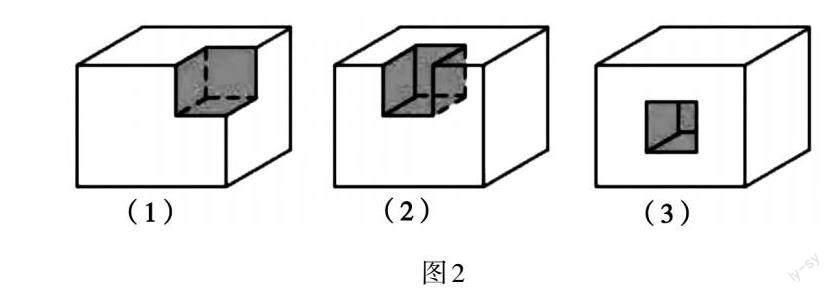
学生由“从顶点挖”想到“从棱上挖”，甚至想到“从面上挖”，如图2：

教师将三种不同挖法同时呈现，引发学生思考：表面积分别怎样变化？体积呢？这是一次深度学习的过程，小小的错题发挥着大大的作用，学生的思维在辨析中不断走向更深刻，呈现出精彩的举一反三[3]。

（三）豁然——于解疑释惑中学会数形结合思想

在对学生的单元疑惑进行分类时，发现大部分学生都提到了长方体或正方体的“切、拼”问题，看来这类问题对学生来说是难题。如何破解此类难题，通过对比不同层次学生的解答过程，发现能正确解答出来的学生几乎都是凭借着示意图的帮助直观地理解问题，可见，数形结合是一种解疑释惑的好方法，学生在运用图形理解和分析问题的过程中逐步学会数学思考，从“惑”走向“豁”。

例1，“把3个完全相同的正方体拼成一个长方体，这个长方体的表面积是350平方厘米，每个正方体的表面积是多少平方厘米？”。

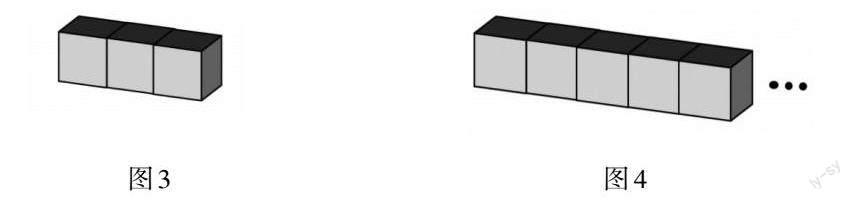
本题只有“350平方厘米”这个显性的数字信息，如何建立长方体和正方体表面积之间的联系，我们需要将拼接后的图形画出来。从图3中可知350平方厘米对应的是14个正方形的面积之和，350 ÷ 14 = 25（平方厘米），一个正方形的面积是25平方厘米，正方体有6个面，因此它的表面积就是25 × 6 = 150（平方厘米）。有了图形的支撑，学生又提出另一种思考的角度：3个正方体共18个正方形的面，拼成一个长方体后减少了4个面，剩余14个面，这14个面的面积总和是350平方厘米，再用350 ÷ 14 × 6算出一个正方体的表面积。教师追问：“如果是5个正方体拼成一个长方体，表面积减少了多少个面？照样这样长条状拼法，n个正方体拼成一个长方体呢？”学生从（3 - 1） × 2 = 4到（5 - 1） × 2 = 8，再到（n - 1） × 2，由具体到抽象，借助数形结合发现规律。

这是拼接，如果是截取呢？出示学生提供的第二个困惑题：

例2，“从一个长方体上截下一个体积是32立方厘米的小长方体后，剩下的部分正好是棱长4厘米的正方体，原来长方体的表面积是多少平方厘米？”（见图4）

本题中仅有两个看似不相关的信息，要求长方体的表面积需要知道长、宽、高，而这三个信息在题目中没有一个是直接告知的，大部分学生无从下手。如果借助数形结合，就能轻松、直观地找出隐藏条件。学生通过画图分析，发现“剩下的部分正好是棱长4厘米的正方体”是本题解题的关键，说明原来的长方体底面一定是一个边长是4厘米的正方形，此时只需再求出长方体的高即可，而截下的小长方体底面也是一个边长是4厘米的正方形，由体积32立方厘米可以求出截下的小长方体的高，这条截下的高加剩下的高就是原来长方体的高，至此，原长方体的长、宽、高已知，就能求出其表面积，问题迎刃而解。

三、课后方法提炼和巩固提升

综上所述，教师应引领学生在知识梳理、绘图分析、易错辨析、困惑解析、方法提炼等数学活动中，让学生对本节课知识点融会贯通、举一反三、数形结合等数学思想方法，在感悟数学思想方法的同时发展学生核心素养，教师可以勾画鱼骨图板书（图5），总结本节复习课主要教学过程。

总之，让学生在复习中学会复习的关键是，教师要让学生学会自主复习，让学生经历自主整理、融会贯通、举一返三等复习过程；同时，教师要给予必要的指导，通过课前知识梳理、课中思维碰撞、课后方法提炼，学生有备而来，教师因材施教，最终达成和谐共长，学生亲历如此持续循环的课前、课中、课后复习全过程，逐步在复习中提升复习力。

[参 考 文 献]

[1]中華人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022：27.

[2]徐世凤.大单元整体教学视域下的小学生量感培育策略——以“面积单位”教学为例[J].中小学教学究，2022，23（05）：35-38.

[3]斯海霞，叶立军.大概念视角下的初中数学单元整体教学设计——以函数为例[J].数学通报，2021，60（07）：23-28.

（责任编辑：杨红波）