从“点、面”到“体”的自主跨越

靳颖

【摘 要】“表面涂色的正方体”属于数学综合实践的教学内容。以学生的生活经验为背景，由“点”到“面”再到“体”的自主跨越，沟通了一维、二维与三维空间的联系，建立了空间观念。学生把在“面”中发现的规律和关系自然迁移到“体”中，降低探究难度。整个探究过程由“面”到“体”、由简到繁、由易到难、由少到多，经历想象和抽象，把思维渐渐引向问题本质，拓宽视觉空间，突破了知识基础和生活经验的限制，促进了学生思维的提升和进阶。

【关键词】数学综合实践 思维 迁移 空间观念

【教学内容】苏教版数学六年级上册第26～27页。

【教学目标】

1.学生把表面涂色的正方体切成若干同样大的小正方体，探究表面涂色的小正方体的各种情况，并发现隐含规律。

2.学生积累探究数学规律的活动经验，初步感悟模型思想，发展数学思维和空间观念。

3.学生在探索数学规律的过程中感受数学实验的价值，获得发现数学规律和学会学习的愉悦体验，激发学习数学的兴趣。

【教学重难点】

探索、发现和表达小正方体中表面涂色面的个数的规律及在大正方体中的位置和彼此之间隐含的规律。

【教学准备】

课件、表面涂色的正方体学具、实验单等。

【教学过程】

一、情境导入，引发问题

师：请看（课件播放学生走方阵表演），同学们正在操场上进行方阵表演庆祝国庆节！几行几列？（生：4行4列）

师：为了方便研究，我们把人看作小圆点，请看课件（课件播放图1）几行几列？（生：2行2列、3行3列、4行4列、5行5列、6行6列）还可能更多行更多列……

课件出示：

师：为了表演的美观，方阵最外圈除了4个角上的同学穿黑色衣服，其他同学穿灰色衣服，除去最外圈的同学，中间的都穿白色衣服。（课件播放点阵图中对应位置的点分别变成黑色、灰色和白色）

课件出示 （●表示穿黑色衣服，▲表示穿灰色衣服，■表示穿白色衣服，见图2）

师：分别说说每个方阵图中黑色、灰色、白色的点各有多少个，并说说你是怎样想的。

【思考】由生活情境引出方阵，逐步呈现2行2列、3行3列等的点阵图，借助生活情境中方阵最外圈4个角上的同学穿黑色衣服，其他人穿灰色衣服，除去最外圈的人，中间的人都穿白色衣服，进而提出问题：“分别说说每个方阵图中黑色、灰色、白色的点各多少个，并说说你是怎样想的”调动学生已有知识基础和学习经验，激发其学习兴趣，使学生借助情境找到自我学习的“舒适区”。

二、唤醒经验，导入新课

（一）点阵图中，初识规律

师：谁来汇报每个方阵中黑色、灰色、白色的点各有多少个，并说说你是怎样想的？

生1：每个方阵中的黑色点都是4个，灰色点分别是4个、8个、12个、16个，白色点分别是1个、4个、9个、16个。

师：每个方阵中灰色的点是怎样计算的？白色的呢？

生2：方阵中灰色点在4条边上，是（每条边上的点子数-2）×4 个；白色点是去掉最外圈后剩下的点，在方阵的中间，是（每条边上的点子数-2）?个。

生3：用n行n列概括所有方阵中每种颜色点的个数，黑色点在方阵的4个角上，灰色点在方阵的边上是（n-2）×4个，白色点在方阵的中间是（n-2）?个。[板书：4 黑（n-2）×4 灰（n-2）? 白]

师：同学们解决了方阵中点的涂色问题，还发现了其中的规律！

（二）方格图中，重现规律

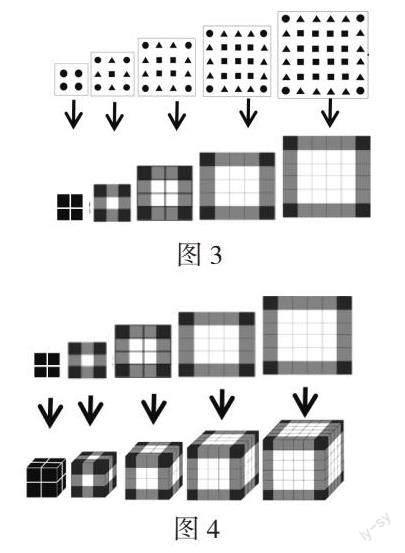
师：请看屏幕（课件播放图3：点阵图中黑色、灰色、白色的点分别变为相应颜色的小正方形，点阵图变成方格图。）发生了什么？

课件出示：

生：点阵图变成了方格图。

师：什么变了？什么没变？

生：小圆点变成小正方形，点变成了面，形状发生了变化，每种颜色图形的个数和所在的位置没变。（板书：面）

师：你能用一句话或一个式子概括出这几个方格图中黑色、灰色、白色的小正方形的个数吗？怎样计算？

生：每个方格图中黑色小正方形都在角上，是4个；灰色小正方形都在边上，是（每条边上的方格数-2）×4个；白色小正方形在中间，是（每条边上的方格数-2）?个。

师：大家同意他的说法吗？谁来再说一遍？如果是10行10列呢？n行n列呢？

生：黑色的都是4个，灰色的是4（n-2）个 ，白色的是（n-2）?个，与方阵的特征和小正方形在方阵中的位置有关。

师：说得真好！同学们通过探究不但解决了方阵图中各种颜色图形的个数问题，还用简洁的式子概括出发现的规律。

（三）立体图中，猜想规律

师：请看课件（课件播放2×2的方格图变成2×2×2的正方体），又发生了什么？

生：面变成了体。（板书：体）

师：（手拿2×2的方格图）这个平面图形有1个面，（手拿2×2×2的正方体）这个正方体有几个面？（生：6个）它的棱等分成2份，切开后等分成多少个小正方体？[生：2×2×2=8（个）]

师：（课件播放2×2、3×3、4×4、5×5、6×6的方格圖分别变成2×2×2、3×3×3、4×4×4、5×5×5、6×6×6的正方体，方格图消失的同时正方体出现，见图4。）正方体的棱等分成几份？（生：2份、3份、4份、5份、6份）

课件出示：

师：（拿起棱等分成3份的正方体）这个正方体的表面涂上颜色，沿着棱切开，得到的每个小正方体会出现怎样的涂色情况？它们的涂色是否和刚才研究的平面图形一样有一定的规律呢？（生举手）

师：都有想法了！这就是我们今天要探究的问题——正方体的涂色问题。（板书课题：正方体的涂色问题）

【思考】先找出方阵中相应颜色点的个数，再由“点”变“面”，点阵图变成方格图，在“什么变了，什么没变”的追问中，学生经过比较发现只是形状发生了变化，位置和每种颜色图形的个数没变，把点阵图中发现的规律自然迁移到方格图中，解决了方格图中的涂色问题。接着，由方格图变为正方体，由“点、面”自主跨越到“体”，提出问题：“正方体的表面涂上颜色，沿着棱切开之后，得到的每个小正方体会出现怎样的涂色情况？它们的涂色问题是否也像刚才研究的点阵图和方格图一样有一定的规律呢？”顺应学生的思维，引发猜想，探究新知。

三、实践操作，探究新知

（一）操作交流，探究问题

师：我们带着刚才的问题继续探究。

课件出示（见图5）：

1.介绍活动要求：每组选两个正方体，探究表面涂色的小正方体的个数，分工合作，做好记录。比一比，算一算，看哪个组最先完成任务，请先完成的小组把你们的研究成果展示在黑板上，并请小组代表汇报你们组的探究成果及想法。

2.学生在音乐声中分工合作，探究交流。（小组展示探究结果，并上台汇报）

组1：我们组探究的是棱等分成3份的正方体的表面涂色问题（拿起棱等分成3份的表面涂色的正方体），切成3×3×3=27（个）小正方体，3面涂色的小正方体在顶点处有8个；2面涂色的在棱上，每条棱上有“3-2”个，12条棱有12个；1面涂色的小正方体在每个面的中间，每个面上有1个，6个面共有6个。大家同意我们组的观点吗？还有什么问题吗？

生2：为什么3面涂色的小正方体都在顶点处呢？两面涂色的都在棱上呢？

组1：顶点是正方体三条棱相交的点，每两条棱组成了一个面，所以三面涂色的都在顶点处。两个面相交成棱，所以两面涂色的都在棱上。

（两个组的代表借助表面涂色的正方体，分别介绍棱等分成4份、5份的大正方体切开后得到的1面、2面、3面涂色的小正方体的个数及探究过程。）

师：耳听为虚，眼见为实！（课件播放）这是棱等分成4份的表面涂色正方体，共同验证1面、2面、3面涂色的小正方体分别在大正方体的哪里？各有几个？

师：（课件播放，验证棱等分成4份的正方体切开后3面、2面、1面涂色的小正方体所在的位置及个数，结合验证过程提问）

课件出示（见图6）：

师：这是              （生：3面涂色的小正方体在顶点处）有几个？（生：共有8个）

课件出示（见图7）：

师：这是              （生：2面涂色的小正方体，在棱上，共有12个）

课件出示（见图8）：

师：这是              （生：1面涂色的小正方体在面上，共有24个）。

师：验证得出我们的探究结果是对的。

【思考】由“点”到“面”再到“体”的自主跨越，建立了一维到二维再到三维的空间观念，沟通了二维与三维空间的联系，突破了知识基础和生活经验的限制，将在方阵图中发现的规律自然迁移到立体图形中，引发猜想：“正方体的表面涂色问题会像平面图形中的涂色问题一样与图形的特征有关且具有一定规律吗？”学生带着猜想探究验证、交流和讨论，解决了棱等分成3份、4份、5份的正方体的表面涂色问题，初步发现3面、2面、1面涂色的小正方体的个数与正方体的特征有关，在“面”“体”的自主跨越中，自然迁移方法，降低了探究难度。

（二）纵横对比 概括规律

师：通过实践操作，我们探究出了棱等分成3份、4份、5份的正方体中各种颜色小正方体的个数。

课件出示（见图9）：

师：观察每一列涂色的小正方体，发现什么？（学生在组内讨论、交流后汇报）

生1：竖着看，小正方体的涂色情况与正方体的特征有关，从第1列看3面涂色的都在正方体的顶点处；从第2列看2面涂色的都在大正方体的棱上；从第3列看1面涂色的都在大正方体的面上。（板书：顶点   棱   面）

生2：横着看，棱等分成3份的3面涂色的小正方体每个顶点处都有1个，2面涂色的每条棱上有“3-2”个，1面涂色的每个面上有（3-2）?个；棱等分成4份的3面涂色的小正方体在每个顶点处都有1个，2面涂色的每条棱上有“4-2”个，1面涂色的每个面上有（4-2）?个；棱等分成5份的3面涂色的小正方体每个顶点处有1个，2面涂色的每条棱上有“5-2”个，1面涂色的每个面上有（5-2）?个。

师：如果棱等分成6份呢？10份呢？100份呢？更多份呢？……

生1：棱等分成6份的3面涂色小正方体每个顶点处有1个，2面涂色的小正方体每条棱上有“6-2”个，1面涂色的小正方体每个面上有（6-2）?个。

生2：小正方体的涂色问题与正方体的特征有关。无论棱等分成几份，3面涂色的小正方体在顶点处，正方体有8个顶点，三面涂色的有8个；2面涂色的在棱上，每条棱上有“n-2”个，正方体有12条棱，两面涂色的有12（n -2）个；1面涂色的在面上，每个面上有（n-2）?个，正方体有6个面，1面涂色的有6（n-2）?个。

[板书：8 （n -2）×12 （n-2）?×6]

师：真睿智！通过观察、对比和想象发现并抽象概括出正方体涂色问题的规律。把掌声送给爱思考的你们！（掌声）

【思考】学生在探究棱等分成3份、4份、5份的表面涂色正方體的基础上，通过纵向观察比较发现3面涂色的小正方体都在大正方体的顶点处，2面涂色的小正方体都在大正方体的棱上，1面涂色的小正方体都在大正方体的面上。学生又通过横向比较发现大正方体的棱不管等分成几份，3面涂色的都在顶点处，有8个；2面涂色的都在棱上，有12（n-2）个；1面涂色的都在面上，有6（n-2）2个。学生通过纵横对比，发现把表面涂色的正方体切成若干个同样大的小正方体后表面涂色的小正方体的各种情况，感悟到正方体的棱等分成的份数不同，变化的只是显性的数量，而变化中不变的却是隐藏的规律，深知万变不离其宗的是特征。由特殊到一般，由直观到抽象，发现并概括规律，学生的思维在探究中不断进阶。

四、运用规律，拓展规律

师：我们探究出了表面涂色的正方体切成若干个同样大的小正方体后，1面、2面、3面涂色的情况及隐含的规律，你们还有什么问题吗？

生1：把棱等分成3份、4份、5份的正方体切开后分成的小正方体的总个数减去1面、2面、3面涂色的小正方体的个数，剩下的是没有涂色的小正方体的个数。如棱等分成3份：3?=27（个），27-8-12-6=1（个），棱等分成4份的……

生2：找1面、2面、3面涂色的小正方体的方法同样适应找没有涂色的小正方体，如棱等分成3份的正方体，（课件播放）正方体的左右、上下和前后面最外层的小正方体剥离掉之后，没涂色的小正方体在正方体的中间是棱为“3-2”的正方体，有（3-2）?=1（个）；所以棱等分成几份，没有涂色的小正方体就有（棱等分的份数-2）?个。

课件出示（见图10）：

师：找出了规律和关系，通过计算就能知道没有涂色的小正方体的个数。请拿出棱等分成4份、5份的正方体验证刚才发现的规律，看没有涂色正方体各有几个。

生：棱等分成4份的正方体切开后没涂色的小正方体是（4-2）?个；棱等分成5份的没涂色的小正方体是（5-2）?个；棱等分成n份的没涂色的小正方体是（n-2）?个，都在正方体中间。

五、回顾总结，拓展延伸

师：这节课我们是怎样探究正方体的涂色問题的？

课件出示（见图11）：

生1：我们的探究由点阵图到方格图，再到正方体，我发现它们的涂色问题都与图形的特征有关。（板书：面 → 体）

生2：我还发现不管是研究点阵图和方格图还是研究正方体的涂色问题，都是由少到多发现规律的。（板书：简 → 繁）

师：真厉害！同学们不但解决了表面涂色的正方体切成若干个同样大的小正方体的表面涂色问题，还发现了隐含的规律，学会了学习。同学们还想研究什么？

生：（齐声）长方体的表面涂色问题。

师：（拿起表面涂色的长方体）请看这个长方体长5厘米、宽4厘米、高3厘米，等分成棱长是1厘米的正方体，猜想一下切开后分成的表面涂色的小正方体会有怎样的情况。

生：我猜想探究长方体表面涂色问题的方法与探究正方体的表面涂色问题的方法一样，长方体的棱等分成若干份切开后得到的小正方体的涂色问题也与长方体的特征有关，3面涂色的小正方体在顶点处有8个；2面涂色的小正方体在棱（长a、宽b、高c）上，有[（a-2）+（b-2）+（c-2）]×4个；1面涂色的小正方体在面上，有[（a-2）×（c-2）+（a-2）×（b-2）+（b-2）×（c-2）]×2个；没涂色的小正方体在长方体的中间，有（a-2）×（b-2）×（c-2）个……

师：这位同学的猜想是否正确呢？我们就带着这个猜想课后继续探究验证。

【思考】学生把表面涂色的正方体切成若干个同样大的小正方体，探究出表面涂色的小正方体的各种情况及隐含的规律之后，及时组织回顾和反思：本节课是如何在自主探究中解决问题的？回顾探究过程，在从“点”到“面”再到“体”的自主跨越中，学生把在平面图形中探究的方法迁移到立体图形中，从“面”到“体”、从少到多解决问题，发现规律，学会学习。当教师追问“你们还想探究什么？”时，学生脱口而出：“还想探究长方体的表面涂色问题。”教师及时追问：“表面涂色的正方体的规律同样适用于表面涂色的长方体吗？”学生的演绎思路随之打开，把正方体表面涂色问题的规律正迁移到长方体中，猜想到长方体的表面涂色问题同样与其特征有关，拓展规律，发掘了潜能，强化了探究学习应有的追求精神。学生在回顾和反思中，进一步积累数学活动经验，感悟活动过程中蕴含的数学思想方法，积淀和发展数学素养。

上述案例，笔者主要是从以下两方面进行思考和教学的：一是精心选用素材，降低探究难度。正方体的涂色问题涉及几何图形，若只是简单地模仿记忆就远离了学生的生活实际，且增加了学生学习的困难。为此，笔者从生活中的庆祝国庆节走方阵表演这个熟悉的生活情境入手，为了便于研究把方阵队伍变为点阵图，接着由点变面、由面变体，这样相继呈现三组学习材料（点阵图、方格图、表面涂色的正方体），新颖且顺应学生的思维特征。由“点”到“面”再到“体”的自主跨越，建立起一维、二维到三维的空间观念。整个探究过程由简到繁、由易到难、由少到多、由“面”到“体”，学生经历了想象和抽象，把思维渐渐引向问题本质，拓宽了视觉空间，突破了知识基础和生活经验的限制，沟通了二维与三维空间的联系，符合学生的认知规律和思维发展顺序，促进学生思维的提升和进阶，降低了探究难度。

二是“面”“体”自主跨越，方法迁移自然。这节课并不满足于学生会利用提升的公式计算各种涂色小正方体的个数，而是在探究和发现规律的基础上自主建构数学模型，做到学会学习。通过找点阵图中的各种不同颜色点的个数，发现规律和关系，正迁移到方格图中，再把平面图中的规律和关系正迁移到立体图形中，引发猜想并通过实践操作探究出表面涂色正方体切成若干相同的小正方体后，小正方体涂色面的个数以及隐含的规律，体验“从特殊到一般”“由简单到复杂”的探究学习，学生的探究逐步深入，知识的学习由薄到厚，“面”“体”自主跨越，方法迁移自然，思维的火花不断碰撞迸发。

【参考文献】

[1]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.

[2]成尚荣.从关注学生现实性走向开发可能性[J].人民教育，2009（8）.

注：本文系江苏省教育科学“十三五”规划立项课题“现行小学数学教材中实践作业资源的深度开发与运用研究”（D/2018/02/178）的阶段性研究成果。