韩芸:“正方体截面的探究”单元教学之课时要素设计

韩芸

[摘  要] 设计基于情境、问题导向的“问题链+任务单”，在情境和情境活动中归纳正方体截面的两种作法——“平行线法”和“延长线法”.

[关键词] 正方体截面的作法;课时要素设计

“正方体截面的作法”是“正方体截面的探究”单元教学之第2课时，在第1课时“正方体截面的形状”的学习中，归纳了正方体截面的六种形状，理解了聚焦正方体的棱与截面交点位置的重要性，通过连接交点形成的线段来确定截面形状.本文以“正方体截面的作法”为例，设计基于情境、问题导向的“问题链+任务单”，在情境和情境活动中归纳正方体截面的两种作法——“平行线法”和“延长线法”.

教学目标

经历观察、发现与证明过程，归纳正方体截面的两种作法——“平行线法”和“延长线法”，增强正方体模型意识;在情境与问题中体验分类讨论、数形结合思想方法，发展直观想象、数学抽象等核心素养.

教学策略

教学重点：利用“平行线法”和“延长线法”作截面.

教学难点：根据已知条件作出正方体的截面.

教学资源：数字化平台、平板电脑.

教学方法：“问题链+任务单”教学法.

学习评价

见表1.

教学流程

略.

教学过程设计

1. 课前学习单

【学习单1】梳理平面的基本性质（三个基本事实和三个推论）和面面平行的性质定理.

【学习单2】正方体的截面不可能是（  ）

①钝角三角形;②直角三角形;③菱形;④正五边形;⑤正六边形.

A. ①②⑤ B. ①②④

C. ②③④ D. ③④⑤

【学习单3】在正方体ABCD-ABCD中，作出过A，C，D三点的截面，作出过A，C，C三点的截面.

设计意图 梳理平面的基本性质（三个基本事实和三个推论）及面面平行的性质定理;回顾上一节课“正方体截面的形状”的学习内容，让学生进一步熟悉正方体截面的形状，感受“棱”与“截面”交点的特殊性，为第2课时“正方体截面的作法”的学习做好准备.

2. 情境引入

【问题1】正方体截面的形状有哪些？

【任务1】请回顾上一节课“正方体截面的形状”的学习过程，交流展示课前学习单.

【追问1】请观察正方体的棱与截面交点的位置，尝试作出正方体的截面.

设计意图 深入理解聚焦棱与截面交点的特殊位置，让学生直观感知正方体中面和面的交线.

3. 探究交流，成果展示

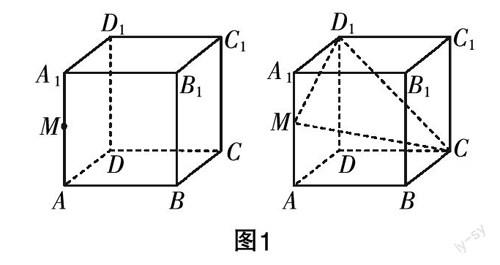
【问题2】如图1所示，已知正方体ABCD-ABCD中，M是棱AA的中点，过点C，M，D作出正方体的截面，并观察截面的形状，交流作法.

【任务2】按所给条件作出正方体的截面，组内交流作法，在班级展示.

【追问2】所给截面图形的边与正方体的位置关系是怎样的？

【追问3】延伸所给的截面，猜想截面会与正方体的哪些面相交？

【追问4】如何找到截面与棱的所有交点，从而得到完整的截面图形？

【追问5】结合平面的基本性质和面面平行的性质定理，说说你的作法.

【追问6】观察所作截面是什么图形，与正方体的几个表面相交？

【追问7】改变点M在棱上的位置，还可以用这些方法作截面吗？

设计意图 设计不同的情境和情境活动，提出合理的问题，直观感知并猜想截面与正方体表面交线的位置，培养学生发现问题、分类讨论、推理论证等能力.

4. 构建数学

【问题3】结合上述作图过程和推理过程，归纳作正方体截面的一般方法.

设计意图 引导学生把握棱与截面交点的位置这一本质，概括作正方体截面的方法——“平行线法”和“延长线法”.

【任务3】学生交流，作图说理验证.

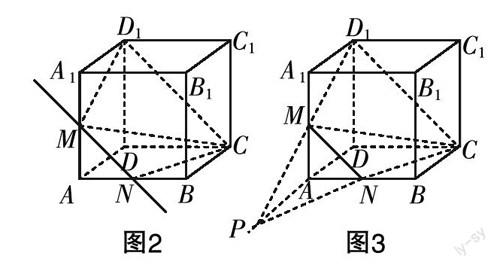
设计意图 如图2所示，根据面面平行的性质定理，过棱上一已知点作已知交线的平行线，找出截面与棱的其他交点，连接交点，得到交线，这种作法俗称“平行线法”. 如图3所示，根据平面的基本事实，通过延长截面与正方体表面的交线和同一平面内的棱，得到交点，由于点在线上，故可得该交点既在截面内又在正方体的表面上，所以该交点一定在截面与正方体表面的交线上，连接正方体同一个表面上性质相同的点，可以作出截面与棱的交点，从而作出交线，这种作法俗称“延长线法”.

5. 学以致用

【问题4】如图4所示，已知正方体ABCD-ABCD中，M是棱AA的中点，N是棱AD的中点，过点C，M，N作出正方体的截面.并观察截面形状，交流作法.

【任务4】类比探究过程，作出正方体的截面，组内交流作法，在班级展示，（结果如图5所示）.

【追问8】所给截面图形的边与正方体的位置关系是怎样的？

【追问9】可以选择哪种方法延伸所给的截面，找到其与正方体棱的交点？

【追问10】观察所作截面是什么图形，与正方体的几个表面相交？

【追问11】当点在棱上的位置发生变化时，截面形状有什么变化？作法会改变吗？

设计意图 设计不同的情境，变换棱上点的位置，虽然截面形状发生了变化，但截面的作法不变，凸显探究问题表现出来的变化中的不变，积累探究问题的通性通法.

6. 目标检测单

【问题5】在正方体ABCD-ABCD中，点M，N，G分别是棱AA，AD，BC的中点.

①过点M，N，G作出正方体的截面;

②求所作截面的面积;

③当点G在BC上运动时，截面可能是什么图形？

设计意图 聚焦正方体模型，让学生深入理解棱与截面交点的位置对截面的影响，通过作图表达进而深层次探究正方体截面面积问题，找到空间图形与平面图形之间的相互转化的联系，引导学生提出可供探究的数学问题，培养学生类比、运用数学知识解决问题的能力.

7. 课堂总结

【问题6】请谈一谈本节课学习了哪些正方体截面的作法，说一说这些作法的依据.

【追问12】请归纳正方体模型的主要性质.

【追问13】谈一谈本节课内容中涉及了哪些数学思想方法和学科素养.

设计意图 回顾梳理2个课时之间的连贯性和整体性，培养学生的分类讨论、数形结合思想方法，提升学生直观想象、数学抽象、逻辑推理等数学核心素养，积累数学探究活动经验，让数学探究成果落地.

8. 課后作业单

在正方体ABCD-ABCD中，点E，F分别是棱BB，BC的中点，点G是棱CC的中点，则过线段AG且平行于平面AEF的截面图形为（  ）

A. 矩形 B. 三角形

C. 正方形 D. 等腰梯形

设计意图 要求学生根据情境作出正方体模型，运用所学知识解决问题.