连续昂贵多目标优化问题综述
张 峰,陈新中
(中国电子科技集团公司第二十八研究所,江苏 南京 210007)
0 引言
许多实际工程优化问题,通常涉及同时优化多个相互冲突的目标,此类问题可称为多目标优化问题(Multiobjective Optimization Problem,MOP)[1-4]。在多目标优化问题基础上,存在一类特殊的问题,其目标函数很难使用公式进行简单计算,而是主要依赖大量耗时的仿真实验进行计算,因而导致优化的时间成本过于昂贵,此类问题可称为昂贵的多目标优化问题(Expensive Multiobjective Optimization Problem,EMOP)[5]。
尽管在最近20 年间,研究者提出大量多目标优化算法以高效地求解各类MOP,但由于多目标优化算法需要进行大量的目标函数评估才能达到理想的求解效果,EMOP每次计算目标函数却比较耗时。另外在求解EMOP 问题时,算法往往只能进行少量的目标函数评估,使得多目标优化算法难以高效地求解EMOP。
为了高效地求解EMOP,许多相关工作开始尝试在多目标优化算法框架基础上,使用机器学习建立代理模型来辅助算法进行评估。在此基础上,涌现出不少专门为高效求解EMOP 而设计的代理辅助进化算法[6]。
目前很少有相关工作回顾该领域的最新技术,现有工作大多根据代理模型对代理辅助进化算法进行分类,通常将相关算法分为基于高斯过程的算法和基于非高斯过程的算法。虽然不同代理模型的特性不一样,在预测不同类型问题的目标值时,预测质量存在一定差异,但都可以用来求解相关类型的问题。在基于代理模型种类的算法分类下,通常难以直观地了解不同类型问题的研究进展。本文按连续昂贵多目标优化问题的规模大小对相关算法进行分类梳理,说明每类问题的特点,分析每个算法的优缺点,以便人们能够直观地了解不同规模的连续昂贵多目标优化问题研究进展,方便后续开展研究工作,或者选择适合的算法求解相关问题。
1 相关基础知识
1.1 连续多目标优化问题定义
EMOP 是在MOP 的基础上,计算目标函数比较耗时的一类MOP 问题。为了方便理解,本文主要介绍MOP。为了更具有普遍性,给出最小化连续MOP 的数学定义如下:
其中,Ω ∈Rn称为n维决策空间,x=(x1,x2,...,xn)T称为一组决策变量,F(x):Ω →Rm则表示需要优化的m个目标函数,Rm为目标空间。下面给出一些关于MOP 的相关定义:
定 义1假 设x1,x2∈Ω,当且仅当∀i∈1,...,m和∃j∈1,...,m,都有fi(x1) ≤fi(x2)和fj(x1) <fj(x2)成立,则称x1Pareto 支配x2[7]。
定义2假设存在解集P,非支配解集PN是所有不被P中的解Pareto 支配的解集。
定义3∃x*∈Ω,若不存在一个解能够使Pareto 支配x*,则称x*是Pareto 的最优解。
定义4在一个MOP 中,所有Pareto 的最优解组成Pareto最优解集(Pareto set,PS)。
定义5Pareto 最优解集对应的目标向量称为Pareto 前沿(Pareto Front,PF)。
1.2 代理模型
一般来说,许多机器学习方法,例如高斯过程[8-10]、多任务高斯过程[11-12]、神经网络[13-16]等,都可用来作为代理模型。算法通常都会从已评估过的解中挑选部分解来训练代理模型。
1.3 效用准则
在通常情况下,许多代理模型对候选解的目标值进行预测时,不仅会给出一个预测目标均值,而且会给出一个预测目标的方差。贝叶斯优化[17]中的效用准则不仅考虑到代理模型的预测目标值,而且考虑到模型预测的不确定性,可用来更好地评估候选解,这对于提升算法的优化性能有着重要意义。
常用的效用准则有EI(Expected Improvement)效用准则、LCB(Lower Confidence Bounder)效用准则和 UCB(Upper Confidence Bounder)效用准则。
1.4 评价指标
EMOP 问题的评价指标[18]主要通过收敛性和多样性来体现。算法在优化EMOP 后,会得到一组解集与解集对应的目标向量。收敛性是指解集对应的目标向量距离Pareto Front 的远近程度,多样性是指解集对应的目标向量覆盖Pareto Front 的完整程度。
2 代理辅助进化算法简介
不同于多目标优化算法对产生的大量解进行目标函数评估,代理辅助进化算法在多目标优化算法框架基础上,使用机器学习建立代理模型来辅助算法评估大量的候选解。候选解可以理解为不经过真实目标函数评估的,由代理模型评估过的中间解。算法最后挑选出少量最有价值的候选解(最佳候选解)进行目标函数评估。反复迭代以上流程,满足算法终止条件后,针对所有进行目标函数评估后的解集执行非支配操作,将得到的结果作为EMOP的近似解集。代理辅助进化算法工作流程如图1所示。
首先,算法根据实际需要对相应参数进行初始化。接下来对算法进行采样,并对采样得到的解进行目标函数评估。然后,在训练代理模型过程中,算法根据设计的策略,从已评估过的解中挑选出部分解作为训练样本,以决策变量作为输入,根据算法设计的需要选择合适的目标作为输出,以训练代理模型。之后,算法将会产生大量候选解,并用代理模型进行评估。算法先产生候选父代,根据父代产生候选子代,使用代理模型评估候选子代中的每个候选解。许多算法通常都会结合贝叶斯优化中的效用准则以更好地评估候选解。上面的过程通常会反复迭代,满足终止条件后则进行下一步骤。最后,挑选最佳候选解主要是从代理模型评估过的大量候选解中,根据算法设计的选解策略,挑选出少量最有价值的候选解进行目标函数评估。反复以上流程,直到满足终止条件(通常指当前目标函数的评估次数达到最大允许值)则停止。
由于代理辅助进化算法的目标函数评估次数一般很少,算法通常对所有评估过的解进行取非支配操作,得到一组非支配解集,这组解集则作为EMOP 的求解结果。
3 代理辅助进化算法分类
本文根据EMOP 的规模大小,将相关算法分成处理小规模EMOP 的代理辅助进化算法和处理中大规模EMOP 的代理辅助进化算法。EMOP 的规模大小主要由决策变量数决定,代理模型虽然对于不同类型问题的预测质量存在差异,但这并不意味着代理模型只适合求解某一类问题。
3.1 处理小规模EMOP的代理辅助进化算法
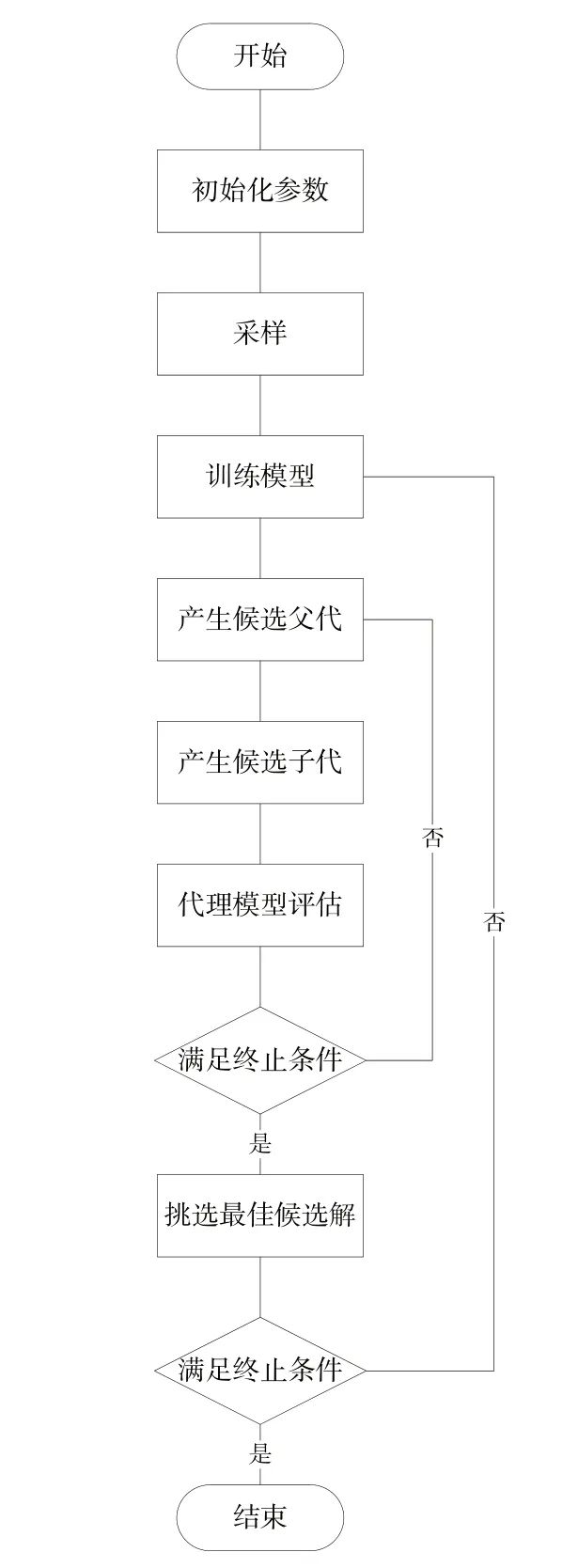
Fig.1 Workflow of surrogate-assisted evolutionary algorithm图1 代理辅助进化算法工作流程
一般称决策变量数较少的EMOP 为小规模EMOP(如决策变量数小于10),通常求解此类问题的目标函数评估次数也较少(如目标函数评估总次数一般在300 次以内)。在小规模EMOP 问题上,高斯过程作为代理模型会拥有比较高的预测质量,并且高斯过程不但可以提供预测目标均值,而且可以提供预测目标方差,能够结合贝叶斯优化的效用准则提升优化性能。因此,选择高斯过程作为代理模型来求解此类问题成为当前的一种流行方法。下面介绍一些主要用来求解小规模EMOP 的算法。
NSGA-II 虽然属于多目标优化算法,但在解决目标变量数较少的EMOP 上有着良好效果,NSGA-II 也经常出现在求解EMOP 的对比算法中[19]。NSGA-II 主要通过对当前种群进行交叉变异产生子代,再通过非支配排序和计算拥挤距离来更新种群,借此不断逼近EMOP 的Pareto Front。
Knowles[20]提出的ParEGO 主要使用一组均匀的权重向量将EMOP 划分成多个单目标子问题,通过优化每个子问题的最优解来近似得出一组EMOP 的最优解。ParEGO实现过程简单,并对许多类型的EMOP 都能取得良好效果,但ParEGO 在一次子问题优化过程中,更多地考虑优化一个子问题聚合函数本身,而不是优化整个EMOP 问题。此外,ParEGO 一次迭代只能产生一个最佳候选解,从而导致ParEGO 求解EMOP 的时间过长。
Ponweiser 等[21]提出的SMS-EGO 采用协方差矩阵自适应进化策略优化一种超体积指标,以决定挑选哪个候选解进行评估,以此不断逼近EMOP 的真实Pareto Front。SMS-EGO 一次迭代同样只能产生一个最佳候选解,并且随着EMOP 优化目标数的上升,超体积指标的计算会变得十分复杂,从而导致算法求解EMOP 的时间过长。因此,SMS-EGO 在求解优化目标数较少的EMOP 时能取得良好效果,而不适合用来求解优化目标数过多的EMOP 问题。
针对一次优化只能评估一个最佳候选解的缺点,在MOEA/D-DE[22]基 础上,Zhang 等[23]提出MOEA/D-EGO。MOEA/D-EGO 通过一组均匀的权重向量把EMOP 划分成多个子问题,MOEA/D-EGO 通过同时优化全部子问题的最佳候选解,并将所有子问题聚类成多个簇,挑选出每个簇的最佳候选解来逼近EMOP 的Pareto Front。MOEA/DEGO 在一次优化中会得到多个最佳候选解,支持使用并行技术同时评估多个最佳候选解,能有效缩短算法求解EMOP 的时间。在优化子问题时,子问题的邻居间进行相互协作,有助于提升最佳候选解的质量。MOEA/D-EGO在求解大多数EMOP 时都能取得比较理想的效果,但在一些特殊问题上,算法效果欠佳,比如优化目标数超过3 的EMOP 等。
针对目标数超过3 的EMOP 优化,在RVEA[24]基础上,Chugh 等[25]提出了K-RVEA。K-RVEA 采用一组自适应权重向量将一个EMOP 划分成多个子问题,K-RVEA 同时优化所有子问题的最佳候选解,并根据代理模型预测结果的不确定性、权重向量分布情况和候选解分布情况,以权衡算法的收敛性和多样性。此外,K-RVEA 还提出一种挑选部分解来训练代理模型的策略,该策略不仅能保证代理模型的预测精度,而且能对代理模型的训练时间进行限制。实验结果表明,K-RVRA 在优化目标数超过3 的EMOP 问题上取得了理想效果。
同样的,针对目标数大于3 的EMOP 优化,Pan 等[26]提出了CSEA。Pan 等认为随着优化目标数的增加,代理模型近似目标函数的计算成本将会变高,因此使用代理模型预测解之间的支配关系会比较适合。CSEA 最终采用神经网络建立代理模型,并使用代理模型预测候选解与参考解之间的支配关系。算法根据代理模型预测的不确定性和支配关系挑选候选解进行评估,最终不断逼近EMOP 的Pareto Front。在求解优化目标数3 及其以上的EMOP 时,CSEA能够取得理想效果。
由于一次优化产生多个最佳候选解可以结合并行技术同时进行评估,从而显著减少求解EMOP 的时间,对于求解时间要求高的应用场景具有比较重要的意义。Lin等[27]提出的MOBO/D 首先通过一组均匀的权重向量把一个EMOP 分解成一组子问题,随后采用MOEA/D-DE 优化出一个候选种群,并进一步使用IGD 指标[28]批量挑选出多个最佳候选解进行评估。通过这些方法可保证算法的收敛性和多样性,因此MOBO/D 在多数EMOP 问题上都能够取得良好效果。随后,Zhang 等[29]在网格约束分解基础上提 出BCDG(A Batched Constrained Decomposition with Grids)。BCDG 采用CDG-MOEA[30]优化出一个候选种群,随后根据hypervolume 指标[31]批量挑选出一些最佳候选解进行评估,通过hypervolume 指标可有效引导搜索方向。BCDG 在求解一些Pareto Front 形状比较复杂的EMOP 时存在一定优势。
随着机器学习技术的快速发展,一部分现有工作开始借鉴迁移学习的一些方法和思想,并将这些方法或思想应用到代理辅助进化算法设计中,借此提升算法的优化性能。
Le 等[32]提出一种交叉代理辅助模因算法CSAMA,CSAMA 首先训练其他目标函数上的代理模型,然后使用训练样本在其他代理模型上的预测结果构建将要进行目标函数预测的目标代理模型,借此提升目标代理模型的预测质量。CSAMA 在求解目标函数相关的EMOP 时可取得比较理想的效果,然而许多EMOP 的目标函数间普遍缺乏相关性,因此CSAMA 不具有普遍性。
针对EMOP 目标函数缺乏普遍的相关性的问题,Luo等[33]提出的GCS-MOE 同样使用一组均匀的权重向量将一个EMOP 划分成许多相关子问题,并进一步将一些相关子问题划分成一个任务组。由于从同一个EMOP 分解出的子问题具有普遍的相关性,因此可更好地结合多任务学习方法优化EMOP。针对多个相关任务组,GCS-MOE 采用多任务高斯过程建立代理模型,算法同时优化多个相关任务组的最佳候选解,以不断逼近整个EMOP 的Pareto Front。此外,GCS-MOE 还提出一种组合效用准则,并为每个任务组的训练样本提供一种选择和维护策略。在求解目标数小于4 且决策变量数不多的EMOP 上,算法取得了理想效果。
针对现有算法将分解后的子问题划分成多个固定任务,未能充分体现任务间相关性的问题,蔡昕烨等[34]提出了AMMCS。AMMCS 同样使用一组均匀的权重向量,把一个EMOP 划分成许多相关的子问题后,通过一种相关性度量指标将这些子问题动态划分成多个相关任务目标。AMMCS 同样采用多任务高斯过程作为代理模型,并使用多种群协作搜索技术同时优化出多个相关任务目标的最佳候选解,不断逼近EMOP 的Pareto Front。AMMCS 在简单、常规的EMOP 上能取得理想效果,但由于预先设置固定的方向向量和代理模型预测质量问题,AMMCS 在一些Pareto Front 形状不规则或者比较复杂的EMOP 上效果不够理想。
3.2 处理中大规模EMOP的代理辅助进化算法
一般称决策变量数较多的EMOP 为中大规模EMOP,此类问题通常需要较多的目标函数评估次数才能进行有效求解(如目标函数评估总次数通常超过300)。随着决策变量数的增加,高斯过程的预测质量会受到影响,并且由于能够获取较多已评估过的解,训练样本相应变得更为丰富。在中大规模EMOP 的目标值预测上,一些机器学习模型的预测质量比高斯过程的预测质量更有竞争力。因此,现有部分算法尝试使用一些非高斯过程的机器学习模型作为代理模型,或者寻找别的方法弥补高斯过程的不足。目前能够高效求解中大规模EMOP 的相关方法较少,主要有以下方法:
针对决策变量数较多的中规模EMOP,Lin 等[35]提出一种可拓展的代理辅助进化算法BS-MOBO。BS-MOBO采用贝叶斯神经网络建立代理模型,并在monte carlo 抽样和sobolov 训练的支持下,能够轻松训练贝叶斯神经网络来辅助算法评估。BS-MOBO 使用MOEA/D 优化出一个候选种群,并根据一种贪婪策略和超体积指标批量挑选出多个最佳候选解进行评估,以此保证算法的收敛性和多样性[36]。值得一提的是,在求解小规模EMOP 问题上,BSMOBO 也可以选用高斯过程作为代理模型,可获得理想的效果。BS-MOBO 的算法性能依赖于一个批量评估最佳候选解的参数,该参数在不同优化问题中,或者在一个完整优化过程的不同优化阶段很可能是不固定的,固定的参数设置很可能会影响BS-MOBO 的算法性能。
针对中规模的EMOP,Ruan 等[37]在高斯过程基础上提出了SAEA/ME。SAEA/ME 挑选相关的决策变量而非全部决策变量参与构建代理模型,并将原来的EMOP 转换为基于代理模型的新问题,同时开发出一种子集选择方法挑选出最佳候选解进行评估,并更新训练样本集。SAEA/ME 在求解决策变量数较多(如决策变量数在10~50 之间)的EMOP 时有着理想效果。由于SAEA/ME 使用NSGA-II 来优化EMOP,在面对优化目标数超过3 的EMOP 时,SAEA/ME 存在一定的争议,并且研究其他降维技术来减轻代理模型构建中的维数灾难,对SAEA/ME 也有着较重要的意义。
4 结语
代理辅助进化算法使用机器学习方法建立代理模型来辅助算法评估候选解,成为求解昂贵多目标优化问题的一种流行方法。因此,对代理辅助进化算法的最新研究进展进行分类总结是一个很有必要的工作。本文根据问题规模大小将相关算法分成两类进行阐述,并分析与比较相应算法的优缺点,希望人们能够从中直观地了解不同规模的连续昂贵多目标优化问题研究现状,方便后续研究工作的开展。

