考虑参数不确定性的驱动电机振动特性分析*

吕 辉，姜 帅，魏政君，曹懿莎

（1.华南理工大学机械与汽车工程学院，广州 510641；2.广西科技大学，广西汽车零部件与整车技术重点实验室，柳州 545006；3.中汽检测技术有限公司，广州 510530）

前言

随着新能源汽车行业的迅速发展，电动车成为国内外汽车行业的研究热点。为适应汽车复杂的运行工况，电动车驱动电机向着轻量化、高转矩密度、高功率密度等方向发展，这使得驱动电机的振动噪声问题日益突出，影响用户的驾乘体验［1］。因此，在驱动电机早期设计开发过程中，需要对驱动电机进行振动特性分析，以抑制电机振动噪声，提高整车NVH性能。

电机振动可以分为机械振动和电磁振动两方面。机械振动由轴承摩擦和转子不平衡等因素引起，电磁振动由作用在结构上脉动的电磁力波引起。相较于机械振动，电磁振动更加突出且不易消除和抑制，是电机振动的主要来源［2］。电磁力波可分解为径向电磁力波和切向电磁力波：脉动的径向电磁力波会引起驱动电机沿径向的振动；而脉动的切向电磁力波会引起电机转矩波动，从而使电机和支架发生侧向振动。目前，针对径向电磁力波的研究主要集中在分析径向电磁力波与电磁振动的关系、径向电磁力波的求解计算等方面：吕长朋等［3］研究认为空载时零阶径向电磁力引起的振动是电机振动的主因；左曙光等［4］建立了有限元模型计算电机的径向电磁力波，并进行了灵敏度分析；刘慧娟等［5］以径向电磁力波为电磁激励源，分析了电机的振动噪声特性；Fakam等［6］考虑永磁体磁导率和转子形状等因素，采用有限元法和解析法混合求解电机的气隙磁场和径向电磁力波。针对转矩波动的研究主要有两个方面：空载下的转矩波动和负载下的转矩波动［7］。空载下转矩波动又称为齿槽转矩，而转矩波动通常指的是负载下的转矩波动，二者需要综合考虑从而达到抑制电机振动的目的。目前，针对转矩波动和齿槽转矩的研究主要集中在分析切向电磁力波与齿槽转矩和转矩波动的关系、电机齿槽转矩和转矩波动优化方法等方面：兰华［8］研究认为，只有零阶切向电磁力波才能对齿槽转矩或转矩波动产生贡献；张立军等［9］研究了由切向电磁力引起的定子齿部切向变形和转矩波动对电磁振动的影响；罗玉涛等［10］以转矩波动等为优化目标对驱动电机结构进行了优化设计。从上述分析可以看出，电机振动特性分析主要是径向电磁力波、转矩波动和齿槽转矩的分析。

上述关于驱动电机振动的分析，多为确定性分析，即其中的结构和材料等参数均视为确定参数。实际上，受制造装配误差、工作温度变化等因素的影响，汽车结构的参数往往存在不确定性。例如制造误差可能造成电机定转子或永磁体的尺寸波动，装配误差可能造成气隙宽度的变化，高转速工况下电机温度升高可能导致永磁体磁性能的变化。这些不确定因素在数值上可能非常小，但多个不确定因素相互耦合就有可能导致电机振动性能发生很大的变化［11］。采用传统的确定性分析方法对驱动电机的振动特性进行分析，可能会导致分析结果产生较大误差。近几年，作者课题组已将参数不确定性模型应用在汽车动力总成悬置系统［12-13］、制动器系统［14-15］的动力学特性研究，并取得了一些成果，这些研究成果表明考虑汽车结构参数的不确定性能使系统响应分析更加合理。因此，有必要对电机振动特性进行不确定性分析。

鉴于此，本文提出了一种考虑电机参数不确定性的振动特性分析方法。首先，基于神经网络代理模型建立驱动电机振动特性的响应模型；然后，结合泰勒级数展开和中心差分法，推导了一种求解驱动电机振动特性不确定响应的高效分析方法；最后，通过算例验证方法的有效性。分析方法能为后续开展系统振动特性的优化设计奠定基础。

1 驱动电机振动特性理论分析

以径向电磁力密度峰值、转矩波动和齿槽转矩峰值来衡量驱动电机的振动性能。

1.1 径向电磁力密度

根据电机学原理，忽略饱和作用时，空载气隙磁场为

式中：f(θ，t)为永磁同步电机空载的气隙磁动势；θ为空间机械角；t为时间；转子磁场谐波次数μ=(2r+1)p，r=0，1，2，…；λ(θ，t)为气隙磁导；Bμ为转子磁场的μ次谐波磁密的幅值为平均气隙比磁导为第k次谐波比磁导；ω1为基波旋转角速度；p为极对数；Z1为定子槽数。

三相电流通过绕组的负载工况下，绕组电流产生的定子磁场为

式中：Bv为定子磁场的v次谐波磁密的幅值；定子磁场谐波次数v=(6s+1)p，s=0，± 1，± 2，…；φ为定子绕组电流的相位。

负载工况下气隙磁场为空载气隙磁场和绕组电流产生的定子磁场之和，即

根据麦克斯韦应力张量理论，径向气隙电磁力密度为

式中：μ0为真空磁导率；br和bt分别为负载工况下的径向和切向气隙磁密。

1.2 转矩波动

在电机负载工况下，转矩波动来源于齿槽转矩、磁阻转矩谐波分量和永磁转矩谐波分量。气隙中的切向电磁力可由麦克斯韦应力张量法计算：

故输出转矩计算公式为

式中：C是气隙中以转子中心为圆心、半径为R的任意圆；L是转子的轴向长度。

转矩波动为

式中：Tmax、Tmin和Tavg分别是一个周期内输出转矩的最大值、最小值和均值。

1.3 齿槽转矩

齿槽转矩是由定子齿和转子永磁体相互作用的切向电磁力产生的转矩，它叠加在输出转矩上，是转矩波动的一部分［16］。电机空载工况下的转矩波动完全来源于电机齿槽转矩。

与电机输出转矩计算类似，齿槽转矩计算公式为

式中bmr和bmt分别是空载工况下的径向和切向气隙磁密。

2 考虑参数不确定性的振动特性分析

工程实际中，汽车驱动电机可能存在这样的不确定情形：定子、永磁体等的结构尺寸由于方便测量，可以获得较为充足的样本信息，适合采用随机变量描述；电机气隙宽度、永磁体材料磁性能等参数由于不易实际获取，缺乏足够的样本数据，宜视为未知但有界的区间变量。

假设电机中存在m个随机变量，组成随机向量x=[x1，x2，…，xm]T；同时还存在n个区间变量，组成区间向量y=[y1，y2，…，yn]T。为便于分析，以F(x，y)、W(x，y)和T(x，y)分别表示随机与区间混合不确定情形下汽车驱动电机的径向电磁力密度峰值、转矩波动和齿槽转矩峰值。

对于制造误差等导致的随机参数，其分布往往符合正态分布［17］。不妨设随机变量xi(i=1，2，…，m)服从均值为、标准差为的正态分布。对于随机向量x，分别用xμ、xσ和V(x)表示其均值、标准差和方差。

输入参数为服从正态分布的随机变量时，系统的输出为概率统计参数确定的随机响应。而对于随机与区间混合不确定情形，系统的输出变为概率统计参数在某一区间的随机响应。即要求解出驱动电机振动特性输出均值和标准差的上下界，才能完全获得混合不确定情形下的驱动电机振动特性响应。

为求解F(x，y)、W(x，y)和T(x，y)的混合不确定响应，以下提出了泰勒级数展开-中心差分法（Taylor series expansion-central difference method，TSE-CDM）和蒙特卡洛法（Monte Carlo method，MCM）两种方法。

2.1 泰勒级数展开-中心差分法

以驱动电机径向电磁力密度峰值F(x，y)为例，TSE-CDM 求解F(x，y)混合不确定响应的过程如下。

首先暂时忽略区间不确定性，仅考虑随机变量的影响，对F(x，y)进行随机不确定分析。假设所有随机变量之间相互独立，将F(x，y)在随机变量的均值处进行1阶泰勒展开［18］，忽略余项，可得

进而，F(x，y)的均值E(F)和方差V(F)为

重新考虑区间不确定性，则式（10）和式（11）所求得均值和方差是区间变量的函数。假设模型的所有区间变量之间相互独立，将E(F)和V(F)在区间变量的中点处进行1阶泰勒展开，忽略余项，可得

由于F(x，y)为关于x、y的隐函数，可通过引入中心差分法计算上式中的偏导数值，得

将式（18）～式（20）3 个方程同时代入式（14）～式（17）中，即可求得混合随机区间不确定模型下的径向电磁力密度峰值F(x，y)的均值和方差的上界及下界，将方差的上界和下界分别开方就得到标准差的上界σ+(F)和下界σ-(F)。类似地，也可求得W(x，y)和T(x，y)的混合不确定响应。

2.2 蒙特卡洛法（MCM）

以驱动电机径向电磁力密度峰值F(x，y)为例，基于蒙特卡洛抽样求解F(x，y)混合不确定响应的过程如下。

（1）按照已知的概率分布，对随机向量x进行p次抽样，生成p组随机向量样本，记为X={x(1)，x(2)，…，x(p)}。对区间向量y在区间范围内进行q次均匀抽样，生成q组区间向量样本，记为Y={y(1)，y(2)，…，y(q)}。

（2）取Y的第b组数据y(b)(b=1，2，…，q)，分别与X中每一组随机向量x(a)(a=1，2，…，p)组合，形成p组输入参数。分别将每组输入参数代入F(x，y)中，共得到p个径向电磁力密度峰值，计算这p个径向电磁力密度峰值的均值E(b)(F)和标准差σ(b)(F)。

（3）重复步骤（2）q次，获得q组E(1)(F)，…，E(q)(F)和q组σ(1)(F)，…，σ(q)(F)的值，进而筛选出均值的上下界、标准差的上下界，分别记为E+(F)、E-(F)、σ+(F)和σ-(F)。

上述蒙特卡洛法分析过程如图1所示。

图1 蒙特卡洛法流程图

同理，上述步骤也可求得W(x，y)和T(x，y)的混合不确定响应。采用蒙特卡洛法求解振动特性的混合不确定响应，须进行p×q次计算。当抽取的样本数目足够多时，可以获得非常精确的响应结果。因此，蒙特卡洛法可以作为TSE-CDM 的参考，验证后者方法的有效性。

3 振动特性响应近似模型

驱动电机振动特性的不确定分析需要计算大量次数的振动响应，大规模地调用有限元模型将不可避免地导致分析计算效率低下。而代理模型技术运用相对简单的模型代替耗时的有限元模型，能大幅提高分析效率。常用的代理模型有响应面模型、克里金模型、神经网络模型等。其中，神经网络模型对非线性模型拟合能力强，有良好的容错率、稳定性、自组织和自适应能力，能够很好地拟合电机振动特性。因此本文引入神经网络模型构建振动特性的代理模型，进而提高不确定性分析效率。

以具有两个隐藏层的神经网络为例，模型输入为驱动电机中的不确定参数，模型输出为驱动电机的振动特性，其结构如图2 所示。每个神经元接受来自前一层神经元不同权重的值，经激活函数处理后向下一层传递。图2 中x=[x1，x2，x3，x4]T为神经网络输入参数；第i(i=1，2，3)层中，w(i)为第i-1层到第i层的权重矩阵；b(i)为第i-1 层到第i层的偏置；z(i)为第i层的净输入；a(i)为第i层的输出。

图2 神经网络结构图

令a()0=x，则神经网络信息传递公式［19］为

式中fi为第i层的激活函数。常用的激活函数有Sigmoid函数、Tanh函数、ReLU函数等。

损失函数表示模型预测值和真实值之间的差异，回归问题中常采用均方误差（mean squared error，MSE）作为损失函数，表达式为

式中：n为样本总数为第k个样本预测值；yk为第k个样本真实值。

损失函数是神经网络参数w(i)和b(i)的函数，因此神经网络的训练是寻找使损失函数最小的w(i)和b(i)的过程。训练迭代的基础方法为梯度下降法，使用反向传播算法可高效地计算梯度，这里不再赘述。

4 算例分析

4.1 驱动电机电磁有限元模型

使用ANSYS Electronics Desktop 电磁仿真软件可求解驱动电机振动特性。以某内置式永磁同步电机为例，其基本参数如表1 所示。在进行有限元仿真计算时，电机模型通常会被简化成2D 或3D 模型，网格划分如图3所示。

表1 电机的研究参数

图3 网格剖分

分别进行驱动电机2D 有限元模型和3D 有限元模型额定工况下的电磁有限元仿真。在定子绕组上施加三相电流激励，得到径向电磁力密度在气隙圆周上的空间分布，如图4（a）所示，输出转矩一个周期内的波动如图4（b）所示，齿槽转矩如图4（c）所示。

图4 有限元仿真结果对比

从图4可以看出，2D和3D模型的仿真结果具有较好的一致性。仿真结果存在差异的原因可能在于2D 模型中存在永磁体端部效应等造成的计算误差。而针对径向电磁力密度峰值、转矩波动和齿槽转矩峰值的计算，2D 和3D 模型的相对差值在5%以内。在计算效率方面，使用同一台计算机，2D 模型的有限元仿真耗时在1 min 以内，而3D 模型的仿真耗时长达数小时。

因此，使用驱动电机2D 模型进行有限元仿真求解振动特性，在满足计算精度的同时，计算效率远远高于3D 模型，故后续采用2D 有限元模型构建振动特性代理模型。

4.2 驱动电机振动特性代理模型

为有效构建神经网络模型作为代理模型，首先使用最优拉丁超立方试验设计方法在参数研究范围组成的空间内采样，研究参数及研究范围如表2 所示。随后，抽取1 000 组最优拉丁超立方样本点，分别代入到电机2D有限元模型，求解出对应的径向电磁力密度峰值F、转矩波动W和齿槽转矩峰值T。最后根据得到的1 000组结果数据构建神经网络模型，其中训练集、测试集和验证集分别占70%、15%和15%。

表2 参数初始值与抽样范围

为避免输入变量数值差异性较大导致训练效果不佳，需在训练前进行数据归一化处理，将所有数据缩放到0 和1 之间。对隐藏层层数和隐藏层神经元个数不同组合得到的不同神经网络模型分别进行训练，比较损失函数最终收敛值的大小，最终采用含一个隐藏层、隐藏层神经元数目为12 的3 层神经网络模型作为振动特性的代理模型。训练过程中的损失函数迭代如图5 所示，训练完成后神经网络模型在测试集上的预测结果如图6所示。

图5 损失函数迭代图

图6 神经网络模型预测结果

从图5 可以看出，经过29 次迭代，训练集、测试集和验证集的均方误差收敛到7×10-4。从图6 可以看出，神经网络模型计算的预测值相对误差较小。其中径向电磁力密度峰值的测试集平均相对误差为0.09%，转矩波动的为0.6%，齿槽转矩峰值的为0.1%，满足精度要求。因此，构建的神经网络模型预测能力和泛化能力均较强，可用于电机振动特性的不确定性分析。

4.3 不确定性情形下驱动电机振动特性分析

考虑参数的不确定性，将定子槽形参数和永磁体结构参数视为服从截断正态分布的随机变量（即忽略掉概率极小的样本），均值为各参数的初始值，标准差为相应均值的0.83%，这样使参数取值范围为围绕均值上下波动±2.5%，即均值±3倍标准差；将气隙宽度、永磁体相对磁导率和永磁体矫顽力视为区间变量，区间中点为各参数初始值，区间半径为各区间中点的5%。不确定参数分布类型和取值如表3和表4所示。

表3 随机变量均值及标准差 mm

表4 区间变量取值边界

采用第2 节中提出的TSE-CDM 和MCM 对驱动电机的振动特性进行混合不确定性分析。蒙特卡洛法在抽样次数足够多时能达到非常高的计算精度，故很多研究将其作为参考方法，用于验证其他数值方法的有效性［20］。使用MCM 求解时，对随机变量和区间变量分别抽取104个样本，即调用神经网络模型计算108次，才能得到收敛的输出响应。两种方法求解得到的混合不确定响应如表5所示。

表5 不确定响应结果对比

由表5 可知，对于驱动电机振动特性不确定响应的求解，除转矩波动的标准差下界外，TSE-CDM的求解误差均在5%以内，而转矩波动的标准差下界的求解相对误差在10%以内，这说明TSE-CDM有着较高的求解精度，能满足一般工程需求。转矩波动的标准差下界求解误差较大，这说明转矩波动的标准差对混合不确定参数的变化更加敏感。计算效率方面，使用同一台计算机，TSE-CDM 的求解时间为6 s，MCM 的求解时间为370 s，可以看出TSECDM的求解时间远小于MCM。

综上所述，考虑参数不确定性对驱动电机振动特性进行分析时，采用TSE-CDM 在保证计算精度的前提下有效提高了计算效率。因此，该方法可有效地应用于后续研究中。

由于驱动电机的振动特性为概率统计参数在某一区间的随机变量，故可基于“3σ”原则计算径向电磁力密度峰值的最大值E+(F)+3σ+(F)、转矩波动的最大值E+(W)+3σ+(W)和齿槽转矩峰值的最大值E+(T)+3σ+(T)。考虑参数不确定性振动分析和确定性振动分析的结果对比如表6所示。

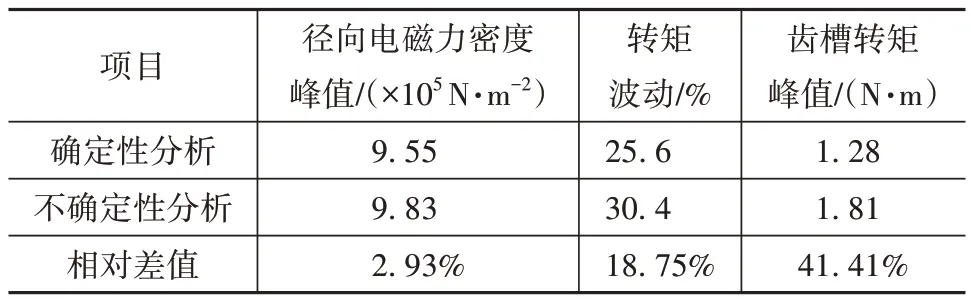
表6 确定性和不确定性分析对比

由表6 可以看出，在不确定参数的影响下，系统振动特性响应的最大值要大于确定性分析的结果。随机和区间不确定性均较小时，齿槽转矩峰值的最大值超出确定性分析结果41.41%，转矩波动的最大值超出18.75%，径向电磁力密度峰值的最大值超出2.93%。可见，混合不确定性对齿槽转矩峰值影响最大，对转矩波动的影响次之，对径向电磁力密度峰值的影响最小。这点在工程中值得重点关注。

本文提出的考虑参数不确定性的驱动电机振动特性分析方法，能有效求得系统的不确定响应，为后续开展系统振动特性的优化改进奠定了必要基础。

5 结论

（1）构建的驱动电机振动特性神经网络模型预测能力和泛化能力均较强，径向电磁力密度峰值的预测集平均相对误差为0.09%，转矩波动的为0.6%，齿槽转矩峰值的为0.1%。

（2）泰勒级数展开-中心差分法能对含随机和区间混合不确定性的驱动电机振动特性的混合不确定响应进行有效分析，在保证精度的前提下大大提高分析效率。该方法能为后续优化设计奠定必要基础。