基于改进GRU模型的高速公路短时交通量预测

温惠英, 元昱青, 赵胜

(华南理工大学 土木与交通学院, 广东 广州 510641)

0 引言

短时交通量预测是根据历史与实时的交通数据对未来临近时间的交通量进行预测。实时准确的短时交通量预测可为出行路径规划、动态交通诱导、交通控制管理等提供数据支撑,有助于提升出行效率,缓解交通拥堵。

传统的交通流预测是以统计分析理论为基础构建模型。它的前提条件是假设预测的未来数据和历史数据具有某种相同的特性。典型的模型主要有历史平均模型[1]、自回归移动平均模型[2]、卡尔曼滤波模型[3]。这类模型大多比较简单,对于具有非线性和不确定性特征的复杂交通流数据,预测精度不高。随着机器学习算法的不断发展,越来越多的学者将机器学习方法应用于交通流预测中。文献[4]运用支持向量机回归模型进行短时交通流预测。文献[5]对K近邻非参数回归模型进行了改进,运用高速公路行程时间数据集进行交通流预测。针对交通流非线性、时间相关性和不确定性等特点,深度学习模型的强大学习能力在处理这些复杂非线性数据方面比其他模型有突出的优势。典型的深度学习模型有卷积神经网络模型、深度信任模型和循环神经网络模型等,其中循环神经网络广泛用于时间序列的预测之中。文献[6]以车辆速度和密度为交通流指标,利用长短期记忆神经网络(long-short term memory,LSTM)构建预测模型。文献[7]运用门控循环单元(gate recurrent unit,GRU)神经网络预测高速公路的速度,并用数字测速数据进行模型的训练。文献[8]提出了一种基于K-means与GRU神经网络相结合的短时交通流预测方法。

目前多数研究对于GRU等神经网络的参数选取方法主要是采用控制变量精细调参、遍历多网格搜索算法,这类方法预测精度较低,计算成本较高,稳定性较差。文献[9]提出一种遗传算法优化神经网络变形预测模型,运用遗传算法优化神经网络参数,对地铁某站点变形数据进行预测。由于群智能优化算法具有寻优精度高且收敛速度快的特性,近年来,许多学者将之运用于神经网络的优化中。在群智能优化算法中,灰狼优化算法(grey wolf optimizer,GWO)较其他优化算法收敛性能更好,同时还有参数少、易实现等特点[10-11]。文献[12]利用灰狼算法对支持向量机的核参数进行优化,提出GWO-SVM分类模型。文献[13]运用灰狼算法优化极限学习机,提出一种GWO-ELM位移预测模型,实验结果表明GWO-ELM位移预测模型在预测性能和泛化能力方面表现良好。

GRU相较于LSTM在结构上更加精简,参数较少,训练效率较高。结合GWO算法在函数优化方面具有较高寻优精度以及良好稳定性的优点,本文针对高速公路交通流量时间序列数据,提出一种基于灰狼算法优化GRU神经网络的短时交通量预测模型。模型训练以预测误差最小为目标,通过灰狼算法对GRU神经网络的参数进行寻优,从而提高GRU神经网络的预测精度,并与支持向量回归算法(support vector regression, SVR)、K近邻算法(K-nearest neighbor, KNN)、LSTM、GRU模型进行对比,结果显示改进GRU模型在交通流短时预测中适应性更好,具有更佳的预测性能。

1 门控循环单元神经网络模型

GRU神经网络是在循环神经网络(recurrent neural network,RNN)的结构上进行了改进以解决长序列训练中出现的梯度消失和梯度爆炸等问题[14]。

图1 GRU单元内部结构Fig.1 Internal structure of GRU unit

GRU与LSTM的基本原理类似,在当前时间步通过门控机制控制输入、记忆等信息而做出预测。为了解决RNN梯度消失的问题,GRU在结构上设置了更新门(update gate)与重置门(reset gate)。这2个门控向量决定了最终门控循环单元的输出,长序列中记忆的信息随时间能够被保存下来。由于GRU只有2个控制门,因此在训练过程中可以降低计算的复杂度,提升训练的效率。

GRU单元内部结构如图1所示,在GRU单元内部包括更新门zt(t为时间步)、重置门rt、候选向量ht′、新状态向量ht。xt为第t个时间步的输入向量。采用矩阵拼接运算与激活函数形成门限。

更新门zt决定了过去记忆的状态信息在当前状态中的保留程度,表达式为

zt=σ(W(z)xt+U(z)ht-1),

(1)

式中:W、U为权值向量;σ为Sigmoid激活函数。

重置门rt决定了以前记忆的状态信息和新输入信息如何相结合,表达式为

rt=σ(W(r)xt+U(r)ht-1)。

(2)

新的记忆内容将通过重置门输出的信息来储存过去相关的信息,表达式为

h′t=tanh (Wxt+rt⊙Uht-1),

(3)

式中:⊙为Hadamard乘积运算;tanh为双曲正切激活函数。

新状态向量ht将保留当前单元的信息并传递到下一个单元中,表达式为

ht=zt⊙ht-1+(1-zt)⊙h′t。

(4)

GRU的训练为前向传播和反向误差传播2个过程。前向传播过程计算GRU单元的输出值,反向误差传播过程计算输出值与实际值的误差,依照梯度下降法,顺着误差梯度减小的方向依次求导更新各层神经元的连接权值,前向传播和反向误差传播2个过程不断交替,直至达到误差最小或最大迭代次数时,迭代过程结束。

2 GWO-GRU短时交通流预测模型

2.1 数据处理

交通流量数据异常主要包括2个方面:一是由于数据采集设备漏采或者通信丢包造成的数据缺失;二是数据采集错误造成的数据突变。针对上述数据异常首先采用插值法对缺失数据进行填补修复,然后采用卡尔曼滤波器对交通流量数据进行降噪处理,消除车流量数据中的高斯噪声,使数据平滑化。

在对交通流数据进行异常值修补以及去噪处理后,需要对数据进行归一化处理,将不同量纲的数据转化为同一量纲的实验数据。本实验采取的是Min-Max归一化法,将数据缩放至[0,1]范围内,并保持数据的原本趋势不变。归一化处理后的数据x(t)的计算公式[15]如下:

(5)

式中:x(t)为交通流时间序列数据;xmin为交通流数据集中的最小值;xmax为交通流数据集中的最大值。

2.2 模型构建

本文对GRU模型进行改进,构建了基于灰狼算法优化GRU的短时交通量预测模型。利用灰狼算法对数据时间步长(time step)、神经网络隐藏层层数(hidden_num)、神经元个数(cell_num)、学习率(learning rate)4个参数在搜索空间进行优化。将神经网络训练的误差值作为适应度函数,利用灰狼算法对神经网络的超参数进行优化,得到最优超参数组合,将交通量数据输入到优化后的GRU模型中,输出可得短时交通量预测值。

Step 1：随机初始化灰狼种群,设置种群数量以及迭代轮次。

Step 2：将交通量数据输入神经网络,设置神经网络训练的误差值作为灰狼算法的适应度函数。

Step 3：采用灰狼优化算法对GRU神经网络的4个参数在搜索空间进行优化,将适应度函数值视为灰狼群体中的猎物位置,计算各个体的适应度值,标记所有个体中适应度最佳的前3个个体位置。

Step 4：当迭代次数不断增加,更新每一个体的位置,并重新计算适应度值。

Step 5：若种群迭代次数满足,适应度函数目标值收敛并达到最优值,则进行下一步;否则返回Step 3。

Step 6：获取搜索空间范围内适应度目标值和最佳参数,计算基于最佳参数的预测误差。

Step 7：将测试数据输入到最优参数组合的GRU网络中,得到预测结果。

改进GRU模型流程图如图2所示。

图2 改进GRU模型流程图Fig.2 Improved GRU model flow chart

2.3 模型评价指标

为了定量分析与评价GWO-GRU模型性能,本文选取平均绝对误差(mean absolute error, MAE)eMA和均方根误差(root mean square error, RMSE)eRMS作为评估指标﹐并与SVM、KNN、LSTM、GRU 4个模型进行对比。MAE和RMSE的值越小,代表模型的预测效果越好。MAE和RMSE的定义表达式[16]分别为

(6)

(7)

3 实例验证

3.1 实验平台和环境

实验平台和环境如下:CPU为Intel(R)Xeon(R)Silver 4208CPU@2.10GHz,GPU为NVIDIA GeForce RTX 3090,内存为94 GB,操作系统为Ubuntu 20.04。实验使用的编程语言为Python,深度学习框架为Keras。

3.2 数据来源和预处理

本文选取广州某段高速公路的匝道出口作为观测点,交通量数据由出口匝道的交通检测器采集获取。时间周期为2020-09-20—29,交通流量采集时间间隔为5 min,2020年9月20日交通流量数据样本见表1。以5 min时间间隔数据为基础,统计时间间隔为15、30 min的交通流量数据,本文采用5、15、30 min 3种时间间隔的交通流量数据进行后续的预测实验。

表1 2020年9月20日交通流量数据样本Tab.1 Traffic flow data sample

以5 min时间间隔数据集为例,取数据集中一周的交通流量数据,将该周每日交通流量数据变化情况展示出来,分析车流量数据在时间上的变化规律,日交通流量变化情况如图3所示。

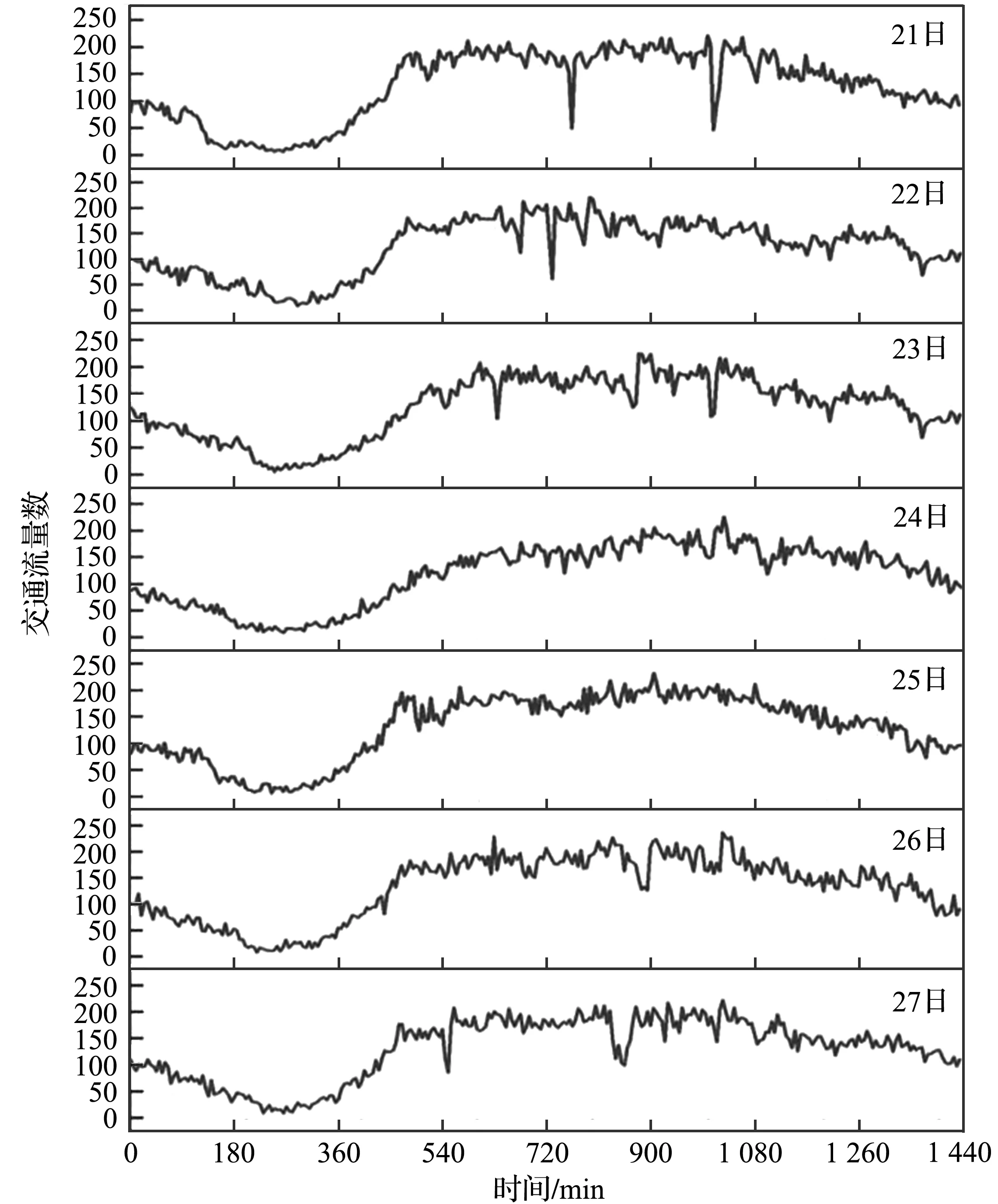
图3 日交通流量变化情况图Fig.3 Map of traffic flow changes

由图可见,交通流数据具有时间周期性,每日交通流量的变化具有相似的变化规律。每日交通量大约从6∶00后开始逐渐增多,7∶00到19∶00维持在较高位,期间有波动起伏,19∶00后呈下降趋势。总体来说,一周的交通流量整体保持着较高的日相似性。交通流量数据经过异常值填补修复和去噪处理,得到的去噪前交通量时间序列(5 min)和去噪后交通量时间序列(5 min)分别如图4、5所示。

图4 去噪前交通量时间序列(间隔5 min)Fig.4 Five-minute traffic volume time series before denoising (5 min interval)

图5 去噪后交通量时间序列(间隔5 min)Fig.5 Five-minute traffic volume time series after denoising (5 min interval)

GWO-GRU模型收敛曲线(5、15、30 min)分别如图6至图8所示。

图6 GWO-GRU模型收敛曲线(间隔5 min)Fig.6 Convergence curve of 5 min interval

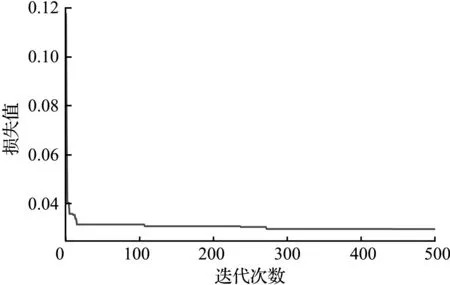
图7 GWO-GRU模型收敛曲线(间隔15 min)Fig.7 Convergence curve of 15 min interval

图8 GWO-GRU模型收敛曲线(间隔30 min)Fig.8 Convergence curve of 30 min interval

3.3 实验结果和分析

运用测试集输入到GWO-GRU模型中进行预测,得到的实验预测结果(5、15、30 min)分别如图9-11所示。由图可知,GWO-GRU模型能较好拟合实际交通流量数据,在交通流量数据突变处趋势转变迅速,显示出较好的预测性能。在5、15、30 min 3种时间间隔的数据集的预测中,时间间隔越小,训练数据量越多,GWO-GRU模型预测的效果越好,表明GWO-GRU模型更适合短时交通流量预测。

图9 高速公路交通流量预测结果(间隔5 min)Fig.9 5 min time interval experiment prediction results (5 min interval)

图10 高速公路交通流量预测结果(间隔15 min)Fig.10 15 min time interval experiment prediction results (15 min interval)

图11 高速公路交通流量预测结果(间隔30 min)Fig.11 30 min time interval experiment prediction results (30 min interval)

运用GRU、LSTM、KNN、SVR 4种模型分别对5、15、30 min 3种时间间隔的高速公路交通流量数据集进行训练和预测,并和GWO-GRU模型的预测结果进行对比。不同模型在3种时间间隔数据集上的数据预测结果对比如图12-14所示。由图可知,5种模型均能较好地拟合高速公路交通流量数据的变化趋势,但在交通流量数据转折处,不同的模型呈现出不同的的预测偏差。GWO-GRU模型对交通流量数据总体变化趋势的拟合效果相较于其他模型更好。

图12 5种模型高速公路交通流量预测结果对比(间隔5 min)Fig.12 Comparison of 5min data prediction results of five models (5 min interval)

图13 5种模型高速公路交通流量预测结果(间隔15 min)Fig.13 Comparison of 15 min data prediction results of five models (15 min interval)

图14 5种模型高速公路交通流量预测结果(间隔30 min)Fig.14 Comparison of 30 min data prediction results of five models (30 min interval)

在3种时间间隔数据集上的不同模型高速公路交通流量的预测精度对比见表2。由表可见,SVR模型在不同数据集中总体的预测效果均偏差,其中30 min数据集相较于5、15 min数据集效果稍好;KNN模型在不同时间间隔数据集的预测中均显示出较好的预测性能,特别在15、30 min时间间隔数据集,预测精度高于GRU、LSTM和SVR3个模型。

表2 不同模型高速公路交通流量的预测精度对比Tab.2 Comparison of prediction accuracy of highway traffic flow among different models

LSTM模型在5 min时间间隔数据集的预测中表现出较好的预测性能,但随着时间间隔增大,训练数据量减少,LSTM模型的预测误差越来越大,说明LSTM模型在3种时间间隔数据集中比较适合短时交通流预测;GRU模型在不同时间间隔的数据集预测中的预测效果相差不大,均具有良好的预测性能,说明在结构上精简改进的GRU模型比LSTM模型预测的稳定性更高,预测效果更佳。GWO-GRU模型在不同数据集中预测的MAE和RMSE均为最小,其预测效果在所有模型中均为最优,体现出该模型良好的适应性和扩展性。在5、15、30 min 3种时间间隔的数据集的预测中,GWO-GRU模型RMSE比次优模型分别降低了3.35%、2.63%、2.07%,其MAE比次优模型分别降低了9.22%、8.54%、8.03%,体现出改进优化后的GWO-GRU模型对短时交通量预测性能的提升作用更加明显。

综上,相比于其他4种模型,GWO-GRU模型可以更好地学习到交通流量数据的特征规律。通过本文的实例验证,GWO-GRU模型能较好拟合出高速公路交通量数据的走势,也具有更好的交通流量预测性能。

4 结论

本文提出一种基于改进GRU模型的高速公路短时交通量预测方法,采用灰狼算法对神经网络参数自适应寻优,从而提高交通流预测的精度和鲁棒性。实验选取高速公路出口匝道的交通流量数据进行预测,结果表明,改进GRU模型的预测效果优于SVR、KNN、LSTM、GRU模型。在5、15、30 min时间间隔的数据预测中,改进GRU模型均表现出良好的预测性能,且时间间隔越小,训练数据量越多,模型预测的效果越好。

本文研究成果对短时交通量预测及预控制有一定积极意义,为出行路径规划、动态交通诱导和交通控制管理提供前期工作的数据支撑。在本文的研究基础上,未来可以将气象状况、节假日等影响因素加进模型之中,增加多个输入变量,建立多元交通流预测模型。此外,本文所用的模型方法可推广至高速公路干线区间路段的交通流预测,以分析高速公路各区间的拥堵状况和提出相应解决方案。