带纵向加强肋复合墙体轴心受压荷载分配规律研究
陈国新, 阿热帕提·艾斯凯尔, 席亮
(1.嘉兴学院 建筑工程学院, 浙江 嘉兴 314001;2.乌鲁木齐建筑设计研究院有限责任公司, 新疆 乌鲁木齐 830092;3.新疆农业大学 水利与土木工程学院, 新疆 乌鲁木齐 830052)
0 引言
带纵向加强肋复合墙体是在普通砌体墙中设置多道钢筋混凝土肋梁来提高墙体性能的一种新型建筑结构形式,如图1所示。因为采用性能优良的保温隔热砌块[1],并把肋梁与边框柱浇筑成一个整体,所以该结构体系是一种即环保又安全的砌体结构体系[2-3],具有成本低、施工设备依赖性不高等优点。

图1 带纵向加强肋复合墙体Fig.1 Composite wall with longitudinal stiffener rib
近年来,国内专家学者对复合墙结构的竖向力学性能进行了广泛研究。王爱民等[4]对密肋复合砌体墙进行了试验研究,结果表明竖向荷载在墙体各部件按照部件刚度来分配 ,其边框柱承担最多的竖向荷载,肋柱次之。董心德等[5]对组合砖墙进行了分析,提出了墙体竖向承载力计算方法和荷载传递规律,为组合砖墙体设计提供了参考。赵丽君[6]对绿色节能复合墙进行了试验研究,结果表明肋柱承担了多部分竖向荷载,并提出了墙体承载力计算公式。董华[7]对密肋复合砌体墙进行了试验研究,结果表明边框柱承担了大部分竖向荷载,砌块承担了较小部分,但其对墙体有支撑作用,与墙体其他部件共同工作来提高墙体承载力。侯莉娜等[8]对生态复合墙体进行试验研究,结果表明各组件分配竖向荷载比例与暗梁、边框柱刚度以及复合墙板等效弹性模量等因素有关,并分析了影响墙体受力分配关系的因素,建立了墙体在竖向荷载作用下的内力计算模型。陈国新等[9]对带纵向加强肋复合墙体进行了试验研究,结果表明洞口对墙体承载能力影响较大,其洞口率影响最明显。
上述研究表明,复合墙体内竖向荷载在各部件中分配传递,边框柱承担墙体多部分荷载,洞口对砌体墙承载能力影响较大,并为各类墙体受压承载力提出了计算公式和分配关系。墙体在实际使用中因功能需求常常会带门、窗洞口工作的,而洞口使墙体整体性削弱,承载能力下降[10]。由于对于竖向荷载在开洞复合墙体中的分配情况和承载力计算方面研究较少,因此,本文中对三榀1/2比例带纵向加强肋复合墙体进行竖向承载力静力试验,以弹性地基梁理论为基础,提出竖向荷载中墙体的简化力学模型,计算墙体各部件所承担荷载,并与试验结果进行对比,分析墙体各部件所分配荷载规律,为墙体在实际工程中的设计与应用提供理论参考。
1 试验概况及结果
1.1 试件设计
制作三榀墙体,编号分别为SCW-1(未开洞)、SCW-2(开门洞)、SCW-3(开窗洞)。墙体实际尺寸为2.8 m×0.2 m×3.0 m(长度×宽度×高度),试验墙体采用1/2缩尺比例制作,尺寸为1.4 m×0.1 m×1.5 m(长度×宽度×高度),边框柱和外框梁截面为100 mm×100 mm(长度×宽度),肋梁肋柱截面为100 mm×50 mm(长度×宽度),各试件墙体尺寸详情如图2所示。边框柱和外框梁配纵筋为4φ6,采用HPB300钢筋,配箍筋为φ4@100,采用冷拔丝,肋梁肋柱配纵筋为4φ4,配箍筋为φ2@100,均采用冷拔丝。

(a) SCW-1

(b) SCW-2

(c) SCW-3
1.2 试件加载
本试验通过100 t液压作动器、竖向千斤顶、加载支架和水平钢梁来完成加载,加载装置如图3所示。

图3 试验加载装置Fig.3 Test loading device
试验采用力控制加载法对试件进行竖向单调加载,分预加载和试验2个阶段完成墙体的加载。预加载阶段每25 kN为一级,分2级对试件施加50 kN荷载,每级保持5 min,施加完再逐级卸载至0。试验阶段,墙体SCW-1每50 kN为一级,墙体SCW-2与SCW-3每30 kN为一级,加载至墙体破坏,每级荷载保持10 min,加载速率为10 kN/min。
1.3 材料力学性能
试验所用钢筋力学性能指标见表1。

表1 钢筋力学性能指标Tab.1 Mechanical property index of reinforced
墙体边框柱、外框梁采用强度等级为C30混凝土现场浇筑,其抗压强度为32.3 MPa,弹性模量为3×104MPa。采用B06蒸压加气混凝土砌块,其抗压强度为3.2 MPa,弹性模量为2.2×103MPa。采用M5.0的砂浆,其抗压强度为7.6 MPa。
1.4 试验结果
1.4.1 墙体荷载-位移关系
在墙体顶部两端和中间位置设置3个位移计读取不同荷载级别下的竖向变形。墙体顶部荷载-位移曲线如图4所示。
从图可知,墙体SCW-1在加载到50 kN之前,顶部几乎没有出现位移,墙体整体性完好;从50 kN加载到175 kN时,墙体荷载-位移曲线呈线性增长,墙体处于弹塑性受力阶段;荷载超过175 kN之后,墙体荷载-位移曲线变缓,墙体处于临界破坏阶段;之后,随位移的增加荷载不再提升,表明墙体破坏。

(a) SCW-1

(b) SCW-2

(c) SCW-3(注:右端位移计脱落)
墙体SCW-2在加载到75 kN之前,顶部位移缓慢增长,墙体两端变形规律基本相同;随着不断加载,墙体各测点变形基本保持线性增长;因开洞不对称导致墙体两侧刚度相差较大,因此刚度大的左侧承担更多的荷载,因而墙体左侧的位移始终大于右侧的。
墙体SCW-3在加载到70 kN之前,顶部位移较平稳增长;竖向荷载从70 kN加载到210 kN过程中位移增长较快,墙体处于弹塑性受力阶段;在继续加载到250 kN过程中,墙体中部位移不随荷载的增加而增长,表明此阶段砌块和肋梁已退出工作,更多的荷载由边框柱来承担,这验证了边框柱提高墙体承载力的作用[11]。
1.4.2 钢筋应变
① 边框柱钢筋。墙体边框柱钢筋荷载-应变曲线如图5所示。

(a) SCW-1

(b) SCW-2

(c) SCW-3
从图5(a)可见,墙体SCW-1边框柱中、底部截面钢筋荷载-应变规律基本相同,可分成3个阶段。加载到150 kN之前,边框柱钢筋荷载-应变曲线呈线性增长,边框柱处于弹性阶段;在加载到200 kN过程中,边框柱钢筋荷载-应变曲线变陡,钢筋应变不随荷载增加而变大,边框柱处于弹塑性阶段;加载到250 kN之后,钢筋荷载-应变曲线增长趋势明显提升,此时边框柱钢筋基本屈服,墙体接近极限荷载。
从图5(b)可见,墙体SCW-2边框柱各截面钢筋荷载-应变规律较一致。加载到30 kN之前,边框柱钢筋荷载-应变曲线呈线性增长;在加载到60 kN过程中,边框柱钢筋荷载-应变曲线变陡;之后随着不断加载,边框柱钢筋荷载-应变曲线基本保持线性增长,因墙体两侧竖向刚度不均匀,导致了左侧框柱钢筋的应变始终大于右侧框柱钢筋的。
从图5(c)可见,墙体SCW-3边框柱左、右截面钢筋荷载-应变规律具有较好的一致性。加载至30 kN时,各钢筋荷载-应变曲线出现拐点;加载到60 kN之前,钢筋出现短暂强化,边框柱处于弹塑性阶段;加载到210 kN之后,钢筋荷载-应变曲变陡,钢筋处于强化阶段,钢筋荷载-应变曲线变缓,边框柱处于临界破坏阶段。
② 肋梁钢筋。试验墙体均设置三道肋梁,通过应变片测出各肋梁纵筋中间的应变,并对其进行分析。墙体肋梁钢筋荷载-应变曲线如图6所示(图中b2、b5和b8分别表示底部、中部和上部加强肋梁中钢筋应变片编号)。

(a) SCW-1

(b) SCW-2

(c) SCW-3
从图6(a)可见,墙体SCW-1的3道肋梁荷载-应变曲线相差较大,底部肋梁钢筋均为受压状态,上部肋梁钢筋均为受拉状态,中部肋梁钢筋受到极小的拉应力,并有过渡到压应力的趋势。加载到50 kN之前,钢筋应变均不大;加载到100 kN之后,荷载-应变曲线出现拐点,此时砌块已退出工作,更多荷载由肋梁承担。
从图6(b)可见,墙体SCW-2中、上部肋梁荷载-应变曲线相差较大,上部肋梁钢筋均为受拉状态,中部肋梁钢筋在加载到250 kN之前不出现应变,之后出现了极小的拉应力。加载到120 kN时,上部肋梁钢筋出现拐点,此时砌块已退出工作,更多荷载由肋梁承担。由于应变片受损,因此未能获取底部肋梁钢筋应变情况。
从图6(c)可见,墙体SCW-3的3道肋梁荷载-应变曲线相差较大,窗洞下端肋梁钢筋均为受压状态,窗洞上端肋梁钢筋均为受拉状态。加载到250 kN之后,荷载-应变曲线出现拐点,此时砌块已退出工作,更多荷载由肋梁承担。
2 理论计算及分析
2.1 简化力学模型及推导公式
把地基假定成均值且连续的弹性半无限体可得到弹性地基梁模型[12]如图7所示,适用处于弹性阶段墙体的变形特征,因此以其为基础,建立墙体的力学计算模型,并假定材料均为弹性材料,外框梁不出现较大变形[13]。

(a) 弹性支座连续梁

(b) 计算模型
根据受力情况把整体梁分为若干段,并在各段梁下施加弹性支座,得到弹性支座连续梁如图7(a)所示。
设弹性支座连续梁有Ki(i= 1,2,…,N)个弹性支座,其中K1,K2,…,Kn(n= 1,2,…,N)为约束移动弹簧刚度,Kn+1,Kn+2,…,Kn+n为约束转动弹簧刚度。为了简化计算,均布荷载替换为集中荷载,设梁受m组荷载Pk、Mk(k=1,2,…,m)。
通过结构力学混合法计算墙体,计算模型如图7(b)所示。先固定弹性支座连续梁一段,再去掉其余支座,用虚力Xi(i= 1,2,…,N)使结构产生原结构一样的角位移φ0和线位移Δ0。由此承载力计算变为支座反力Xi、角位移φ0和线位移Δ0的求解。
由支座变形条件得
(1)
(2)
由平衡条件得
(3)
(4)
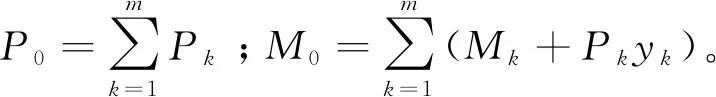
因为梁端转角φ0很小,所以取式(1)中tanφ0=φ0。联立式(1)至式(4),可得连续梁基本力学方程

(5)
式中:δij为Xj(j=1, 2, …,N)方向产生的位移;Δip为Xi方向产生的位移。分别根据不同情况来计算:
① 当Ki、Kj均为约束移动弹簧时,有
(6)
② 当Ki、Kj均为约束转动弹簧时,有
(7)
③ 当Ki为约束移动弹簧,Kj为约束转动弹簧时,有
(8)
④ 当Ki为约束转动弹簧,Kj为约束移动弹簧时,有
(9)
⑤ 当Ki为约束移动弹簧时,有
(10)
⑥ 当Ki为约束转动弹簧时,有
(11)
求解式(5)可得出任一支座的支座反力Xi。
2.2 反力计算及结果分析
2.2.1 反力计算
根据等效弹性板理论[14]和本课题组前期研究成果[15],把处于弹性阶段的墙体等效为弹性板,并将其视为双向纤维模型,墙体等效模型如图8所示。根据前期研究成果,等效板弹性模量由式(12)计算[16]。

(a) SCW-1

(b) SCW-2

(c) SCW-3
E=ηEcVc+EqVq,
(12)
式中:η为修正系数,取0.7;Ec、Eq分别为混凝土、砌块弹性模量;Vc、Vq为混凝土、砌块体积分数。
将边框柱除外部分等分为6个等效板。计算外框梁抗弯刚度EI=250 kN·m2,边框柱刚度K7=2×105kN/m,外框梁受转动约束刚度K8=250 kN·m2。由式(12)计算各等效板弹性模量,并考虑边框柱加强的影响。墙体各等效板刚度见表2。墙体计算模型如图9所示。

表2 墙体各等效板刚度Tab.2 Stiffness of equivalent panels of the wall

(a) 等效弹性支座

(b) 支座反力计算模型
为了分析竖向荷载在墙体内的分布情况,由式(13)计算边框柱所受荷载。
σs=εEs,σc=εEc,f=σsAs+σcAc,
(13)
式中:σs、σc分别为钢筋和混凝土应力;Es、Ec分别为钢筋和混凝土弹性模量;As、Ac分别为钢筋和混凝土面积;f为边框柱承担荷载值;因假设混凝土与钢筋之间没有滑移,因此应变取钢筋试验值。墙体SCW-1、SCW-2、SCW-3计算与试验结果分别见表3至表5。

表3 墙体SCW-1计算与试验结果Tab.3 Calculation and test results of wall SCW-1
2.2.2 结果分析
由试验与计算结果可知,三榀墙体边框柱荷载试验值与理论计算值最大相对误差为14.7%、平均误差为10.2%,即理论计算具有一定的准确性。
试验结果表明,三榀墙体边框柱在竖向荷载下所分配的荷载比例均值分别为55.2%(SCW-1)、58.1%(SCW-2)、57.6%(SCW-3),带洞口墙体边框柱所分配的荷载比例均高于未开洞墙体和三榀墙平均值56.9%。
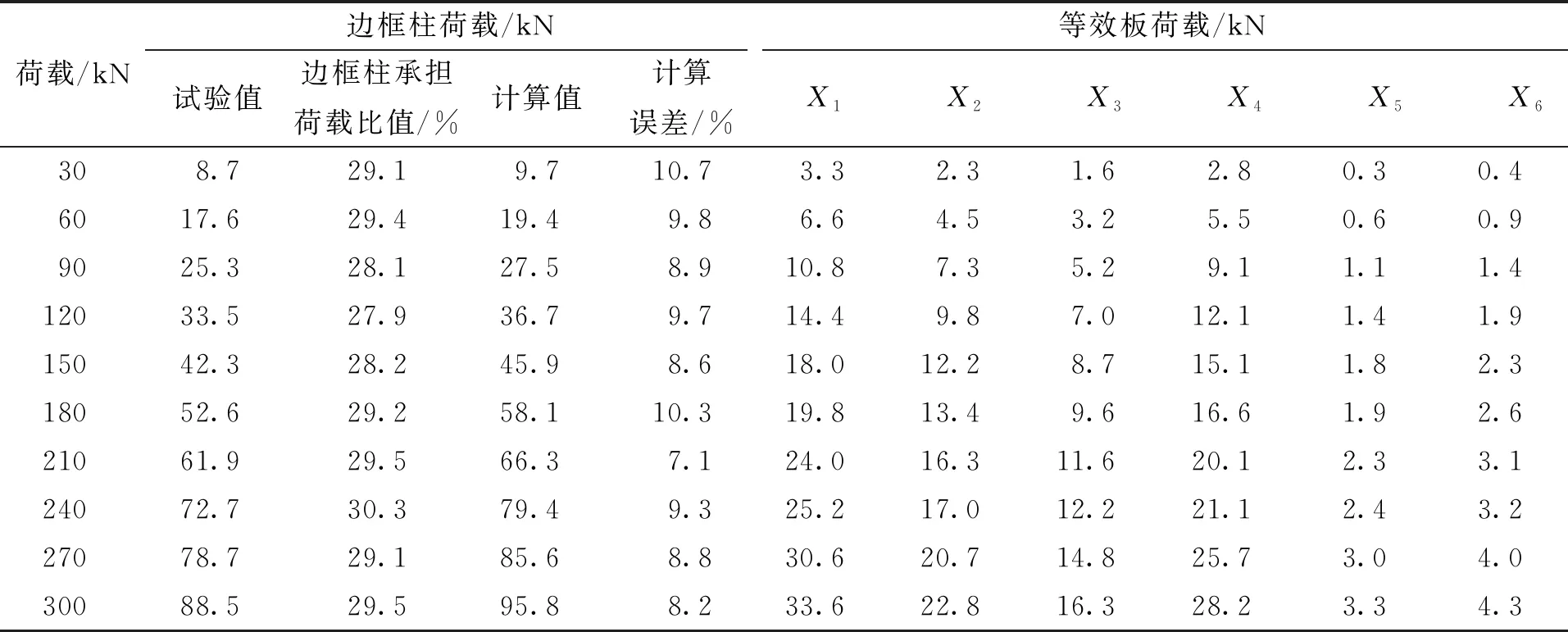
表4 墙体SCW-2计算与试验结果Tab.4 Calculation and test results of wall SCW-2

表5 墙体SCW-3计算与试验结果Tab.5 Calculation and test results of wall SCW-3
墙体各部件荷载分配变化规律如图10所示。由图10(a)与计算结果可见,整个加载过程中墙体SCW-1边框柱承担了51.4%~57.3%的竖向荷载,墙体各部件所承担的荷载变化曲线呈线性增长,随着荷载的不断增加墙体各部件所承担的荷载比值基本不变,其中边框柱承担的荷载最大,墙体中间砌块承担的荷载最小。
由图10(b)与计算结果可见,整个加载过程中墙体SCW-2边框柱承担了55.8%~60.6%的竖向荷载,墙体各部件所承担的荷载变化曲线呈线性增长,随着荷载的不断增加墙体各部件所承担的荷载比值基本不变,其中边框柱承担的荷载最大,墙体左端砌块和肋柱承担的荷载次之,中间砌块承担的荷载最小,加载到120 kN之后,门洞上部砌块承担极小一部分的荷载。
由图10(c)与计算结果可见,整个加载过程中墙体SCW-3边框柱承担了55.7%~60.4%的竖向荷载,墙体各部件所承担的荷载变化曲线呈线性增长,随着荷载的不断增加墙体各部件所承担的荷载比值基本不变,其中边框柱承担的荷载最大,洞口边砌块承担的荷载最小,加载到60 kN之后,洞口上下部砌块承担极小一部分的荷载。
从试验与计算结果来看,墙体SCW-1边框柱在加载初期承担的荷载比值最小为51.4%,这时砌块承担的荷载比值最大,荷载达到100 kN时,边框柱承担的荷载比值达到最大为57.3%,这时砌块少承担了一部分荷载,之后随着荷载的增加边框柱承担的荷载开始减少,直到墙体破坏边框柱所承担的荷载一直在55%左右,砌块承担荷载也比较稳定。
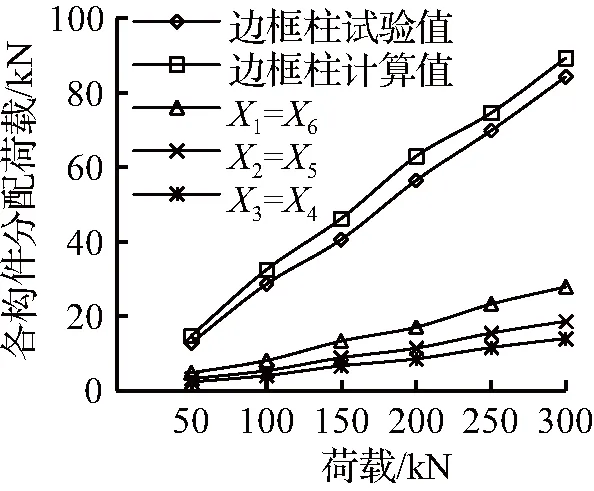
(a) SCW-1

(b) SCW-2

(c) SCW-3
墙体SCW-2边框柱在加载初期承担的荷载比值为58.1%,随着继续加载,承担的荷载逐步减小,直到120 kN时,所承担的荷载比值降到55.8%,这时砌块和肋柱承担的荷载增大,在加载达240 kN时,边框柱承担的荷载比值达到最大为60.6%,砌块和肋柱所承担荷载减小,加载由240 kN到墙体破坏,边框柱承担的荷载比值略有减小,砌块和肋柱承担的荷载增大。
墙体SCW-3边框柱在加载初期承担的荷载比值最大为60.4%,这时砌块承担的荷载比值最小,随着荷载的不断增加,边框柱所承担荷载不断减小,砌块所承担荷载不断增大,直到120 kN时,边框柱所承担的荷载比值降到最小为55.4%,这时砌块承担的荷载比值达到最大,之后随着荷载不断增加,边框柱承担的荷载增大,墙体破坏时,承担荷载比值为58.2%。
以上情况表明墙体所受大部分竖向荷载由边框柱来承担,尤其在开门洞墙体边框柱承担的更多,开窗洞墙体边框柱其次,可视为墙体的主要承重部件。
总的来看,三榀墙体各部件按照轴向刚度来分配竖向荷载,整个过程中墙体各部件所承担的荷载比值基本不变,其边框柱承担了大部分荷载,墙体中间砌块承担荷载最小,洞口上下部砌块在荷载达到一定值后承担极小一部分的荷载,洞口增大了边框柱所承担荷载的比值,导致墙体的承载能力有所下降,尤其在洞口非对称布置时影响更大,但肋梁降低了洞口对墙体的影响,提高了墙体承载能力,因此,在进行墙体设计时应尽量避免开非对称洞口,开洞时考虑加设洞边肋柱。
3 结论
① 在竖向荷载作用下边框柱各截面钢筋具有基本相同的应变变化趋势,三道肋梁钢筋应变变化有所不同,其底部肋梁钢筋均处于受压状态,上部肋梁钢筋均处于受拉状态,而中部肋梁钢筋应变变化较小,应力基本处于临界状态。
② 以弹性地基梁理论提出的墙体简化力学模型和计算方法合理可行,理论计算具有一定的准确性。
③ 在竖向荷载作用下墙体各部件按照轴向刚度来分配竖向荷载,各部件所承担的荷载比值基本不变,其边框柱承担的荷载最多,墙体中间砌块承担荷载较小。

