基于MCC盾构下穿施工对既有隧道的影响研究
汪溯, 袁立凡, 马壮
(1.沈阳地铁集团有限公司, 辽宁 沈阳 110011;2.沈阳建筑大学 交通与测绘工程学院, 辽宁 沈阳 110168;3.江苏中设集团股份有限公司, 江苏 无锡 214000)
0 引言
在新建盾构隧道近距离下穿既有隧道施工时,隧道之间不同的净距和空间位置关系,带来的相互影响皆会不同[1],解决问题的关键在于,正确得到新建隧道下穿施工对既有隧道受力和变形等的变化规律及影响程度[2]。丁智等[3]、Huang等[4]和Yang等[5]通过理论解析和模型试验等方法取得了很多研究成果,但是仍不能较为真实反映施工开挖的动态过程。数值模拟则可以很好地弥补这一短板,Lin等[6]、孙雅珍等[7]和杨平等[8]都采用此法得到了许多建设性成果,主要聚焦在新建隧道开挖对周边的影响或周边开挖卸载(堆载)对既有隧道的影响,但通常没有考虑土体的回弹、压缩及非线性问题,且对于研究穿跨越既有隧道过程中的动态影响稍有欠缺。基于此,本文针对长三角软土地质条件下的新建地铁盾构隧道,以上海轨道交通为工程背景,综合考虑下穿跨越既有隧道的交叉问题,通过ABAQUS有限元软件,依据上海软土地质条件采用非线性土体本构模型—修正剑桥弹塑性模型[9],针对新建隧道施工引起的土体扰动所带来的应力场改变导致既有隧道的受力情况、变形情况和地表特征发生变化,对动态掘进过程中的影响进行研究,避免多种因素改变带来的影响叠加而产生地表沉陷和衬砌结构变形过大等危害,为工程设计和施工监测提供参考。
1 工程背景
上海市轨道交通15号线土建工程下穿9号线地铁近接工程(桂林路站),15号线新建隧道穿越9号线投影长度24 m,上行线穿越段为524~544环,距离9号线垂直距离最小为1.8 m,最大为2.2 m,上行线环宽为1.2 m,共计20环。
15号线上行线自西向东推进,覆土厚度为-17.696 m,隧道管片外径为6.6 m,内径为5.9 m,管片厚度为0.35 m。运营9号线隧道管片外径为6.2 m,内径为5.6 m,管片厚度为0.3 m。穿越段隧道平面为直线,交叉角度接近于正交90°。
区间隧道平面位置关系和区间隧道剖面位置关系分别如图1、2所示。

图1 区间隧道平面位置关系Fig.1 Relation of planimetric position of section tunnel
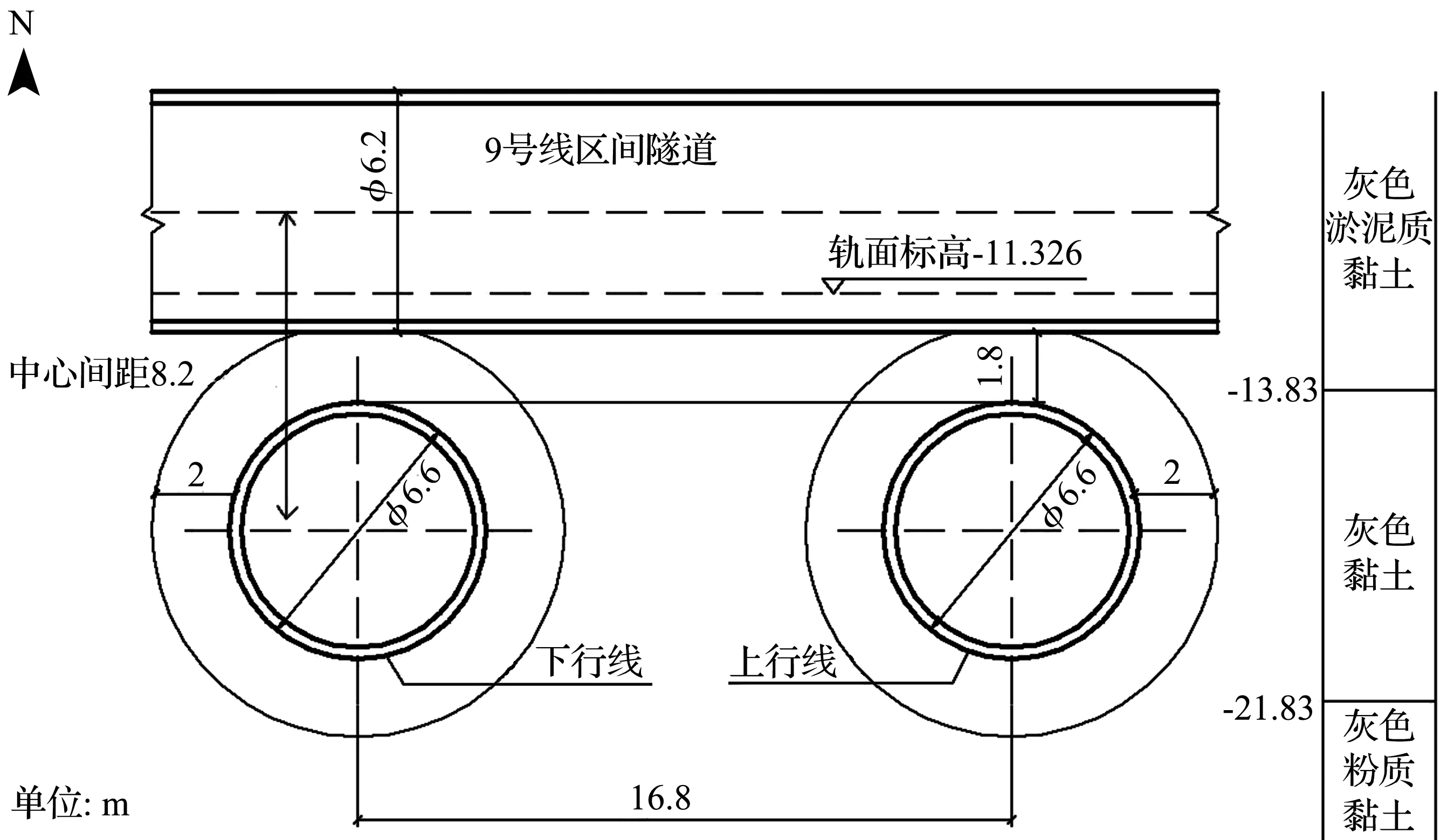
图2 区间隧道剖面位置关系Fig.2 Relation of profile position of section tunnel
15号线所处土层主要为灰色黏土和灰色粉质黏土层,9号线所处土层为灰色淤泥质黏土层。
2 修正剑桥弹塑性本构理论
针对软弱土层的高压缩特性,应用修正剑桥非线性本构模型(modified Cam-clay, MCC)结合多孔弹性模型来模拟土体的弹塑性。剑桥模型以临界状态土力学为基础[10],用来模拟非黏结性材料。材料的屈服函数考虑了第三应力不变量,使用屈服面相适应的流动规则,塑性体积应变被视为硬化参数;弹性部分参数与多孔弹性模型或线弹性结合使用;强化准则定义为指数函数形式[11]。

图3 主应力空间的MCC模型屈服面和临界状态面Fig.3 MCC model yield surface and critical state surface in principal stress space
MCC模型作为典型的塑性本构模型,能模拟剪缩,但不能模拟剪胀,其屈服面是一个椭圆曲线,主应力空间的MCC模型屈服面和临界状态面如图3所示。其方程[12]为
(1)

由于修正剑桥模型为典型的塑性模型,需要与多孔弹性模型结合使用,因此屈服面大小需要由初始硬化参数a0和塑性体积应变来确定。
(2)
其中:e0为初始孔隙比;Jpl为塑性体积变化;λ为压缩曲线斜率;κ为回弹曲线斜率。
3 盾构下穿既有隧道的影响研究
3.1 盾构下穿既有隧道智能监测
以上海轨道交通为工程背景,对15号线下穿9号线桂林路站区间的整体动态开挖过程进行智能监测,通过监测数据对开挖过程进行及时调整,同时揭示新建隧道正交下穿既有隧道衬砌变形、隧道内力等变化规律,并将实际监测数据与数值模拟结果进行对比分析,也验证了数值模拟的可靠性。
监测采用电水平尺组成的“尺链”及相应的CR系列数据自动采集器组成的竖向位移自动监测系统,进行实时监控,并根据监控数据,指导并优化施工过程。电水平尺链沿9号上行线轴线布置在地铁轨道中间、拱底位置处,每一个9号线管片设置一个监测点。
3.2 盾构下穿既有隧道数值模拟
3.2.1 三维有限元模型建立
根据已有研究成果及隧道力学中隧道的影响范围[13],本文边界取尺寸为60 m×45 m×50 m(长度×宽度×高度),x、y、z轴分别表示新建隧道轴线、既有隧道轴线和土体自重方向。
新建盾构隧道交叉下穿既有隧道示意图及工况①时盾构隧道土体三维有限元网格分别如图4、5所示。模型约束设置为:前、后边界和左、右边界均为水平约束;底部边界为固定端约束。土体和衬砌单元为C3D8R,盾构机为壳单元S4R。除此之外,我们假定:①在开挖前,前期沉降已趋于稳定;②小变形假定;③除盾构机入土外,其余每步开挖均为一环衬砌1.5 m,衬砌材料为线弹性;④弹塑性假设:围岩土体为非线性材料,采用MCC Model。

图4 新建盾构隧道交叉下穿既有隧道示意图Fig.4 Schematic diagram of new tunnel undercrossing existing tunnel

图5 工况①时盾构隧道土体三维有限元网格Fig.5 3D finite element mesh of shield tunnel soil under working condition I
3.2.2 材料参数
① 土体修正剑桥模型参数[14]见表1。

表1 土体修正剑桥模型参数Tab.1 Parameters of MCC model
② 岩土模型参数见表2。

表2 岩土模型参数Tab.2 Parameters of geotechnical model
③ 衬砌参数
为了能够真实地模拟管片接头对衬砌强度的影响,对衬砌进行刚度折减,本文折减为原始刚度的85%。盾尾注浆弹性模量根据龄期的增长可分为3个阶段:初始液态浆液阶段、1 d固化阶段和28 d固化阶段,其弹性模量分别约为0.9、5.0、300.0 MPa,因本文中主要研究开挖阶段的影响,故着重考虑初始注浆段到1 d固化阶段浆液弹性模量的变化,并在ABAQUS中采用子程序USDFLD定义1个场变量实现盾构开挖过程中注浆材料弹性模量时变性[15],衬砌材料、注浆及盾构机参数见表3。

表3 衬砌材料、注浆及盾构机参数Tab.3 Lining materials, grouting and shield tunneling machine parameters
3.3 工况设置
根据实际工程情况,本文隧道外径取值为6.0 m,衬砌厚度为0.35 m,浅埋深度设为4 m,深埋深度设为13 m。土层主要为黏土。根据实际工程经验,盾构舱内支护掌子面开挖土体的土压力为0.10~0.25 MPa,取0.15 MPa。在推进过程中盾尾需同步注浆,注浆压力范围为0.1~0.3 MPa[16],取0.25 MPa。不同工况下净距设置见表4。
3.4 盾构开挖过程动态模拟
ABAQUS模拟盾构隧道开挖过程,主要通过以下步骤:①进行地应力平衡,本文中地应力平衡的量级为10-5;②首先模拟盾构机进入,向掌子面施加支护力,然后逐步推进;③采用“生死单元法”,对开挖土体进行“杀死”来模拟土体开挖,随后“激活”盾构机单元;④“激活”对应位置的衬砌和同步注浆单元,“杀死”上一步中激活的盾构机单元;⑤重复步骤③和④,直至开挖完毕,盾构机出土后移除注浆压力模拟注浆体固结。
3.5 实测数据与数值模拟数据对比分析
考虑到监测数据所处的实际工程条件,在与数值模拟结果对比中,数值模拟的相关数据均提取自工况①的数据,监测数据提取自9号线上行线推进过程中的数据。
由于盾构穿越前在9号线影响区范围以外第483~514环进行试推进阶段,9号线监测几乎无沉降记录,因此数据从15号线隧道推进到第512环开始提取。
既有隧道结构沉降对比分析如图6所示,通过9号线上行线测点位置处的推进过程沉降曲线与数值模拟的推进过程沉降曲线进行对比,发现在整体趋势方面呈现出较好的吻合,更好地证实了在结构正下方穿越推进时影响最大。

图6 既有隧道结构沉降对比分析Fig.6 Comparison and analysis of subsidence of existing tunnel structure
可以看出,无论是数值模拟还是实测数据,当处于盾构下穿阶段时既有隧道沉降趋势最为明显,最大沉降模拟值和实测值分别为-4.02、-4.11 mm,且在穿越结束后,既有隧道沉降值会略微减小,这是由于当新建盾构隧道下穿双孔隧道时,在下穿下行线时,由于下行线的结构对土体提供了一部分刚度加持。
4 多参数影响分析
4.1 浅埋条件下新建隧道下穿既有隧道施工影响分析
为了探究浅埋条件下新建盾构隧道下穿既有隧道施工时,两隧道间净距改变对既有隧道的影响,分析净距分别为0.5D、1.0D、1.5D、2.0D、3.0D时的位移与内力情况。
4.1.1 地表沉降分析
工况①-⑤既有隧道地表沉降曲线如图7所示。从图可以看出,当盾构机在既有隧道正下方时,沉降值最大。对于工况①-⑤,即新建隧道与既有隧道净距为0.5D~3.0D时,竖向位移的增大速率会减缓。其原因为,既有隧道属于浅埋隧道,新建隧道施工开挖使得地下土体承载力减弱,导致既有隧道在该处产生沉降。
当净距由0.5D增大到2.0D时,最大沉降值相继增大了0.52、0.46、0.23 mm。可以认为,土体本身也具有承载力,当净距增大到一定数值时,轴线位置处沉降也会逐渐开始放缓,不会随着深度的增大而无限增大。
工况①-⑤新建隧道地表竖向沉降曲线如图8所示。从图可知,在新建隧道盾构施工开挖过程中,最小沉降值出现在既有隧道下方。由于既有隧道的存在对土体的刚度提供了一定加持作用,因此在既有隧道周围两侧5环管片长度处,沉降趋势表征出随净距增大而逐渐增大的趋势。

图7 工况①-⑤既有隧道地表竖向沉降曲线Fig.7 Vertical settlement curves of the existing tunnel surface of working conditions Ⅰ-Ⅴ

图8 工况①-⑤新建隧道地表竖向沉降曲线Fig.8 Vertical settlement curves of the new tunnel surface of working conditions Ⅰ-Ⅴ
沿新建隧道开挖方向,盾构入口处沉降大于出口处,且盾构入口处的沉降值,随着净距的增大而不断减小。分析其原因,随着盾构器械的不断掘进,入口处周围土体的扰动大于出口处,导致入口处地表沉降大于出口处的,并且由于2条隧道净距的增大,施工时对周围土体的扰动程度减小,造成的地表沉降也越小。
以工况②典型断面为例,盾构掘进过程土体竖向位移云图如图9所示。可以看出,新建隧道拱顶以上和拱底以下的土体区域竖向位移比较集中,其范围随着掘进过程不断扩展,但盾构机在掘进过程中的影响区域是有限的。

(a) 开挖6环
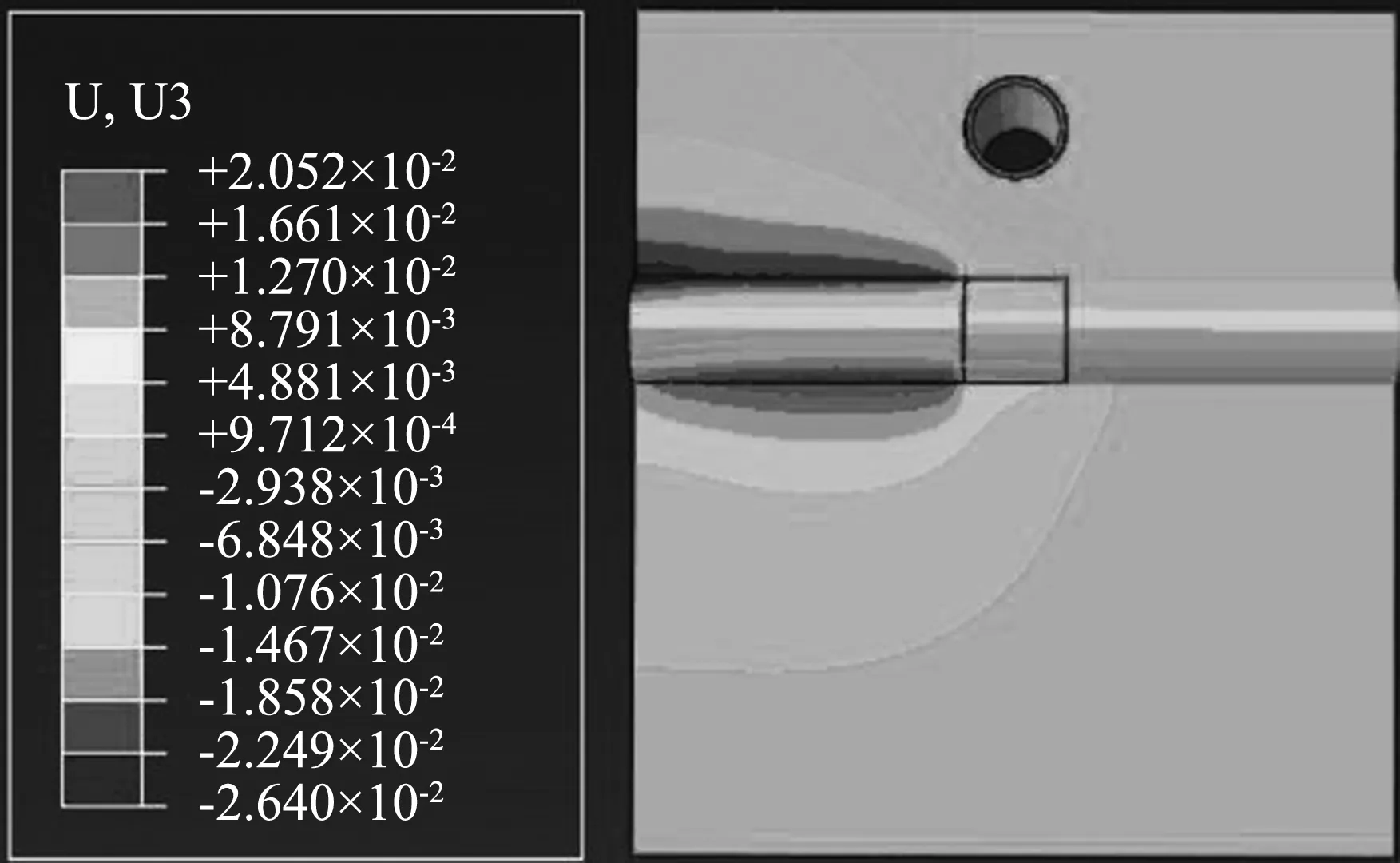
(b) 开挖13环

(c) 开挖22环

(d) 开挖结束
4.1.2 管片位移分析
工况①-⑤时所取截面管片相对位移曲线如图10所示。由图可见,整体的变形呈现出一种扁鸭蛋的形状,即左、右两侧拱腰内凹,下侧外凸的形状。新建盾构隧道盾构机入口一侧的水平位移值略大于出口一侧;外凸变形发生在拱底处,位移最大处发生在拱底位置,最小处发生在拱顶位置。
在工况①-⑤中既有隧道管片拱底位置处相对位移值分别增大了53.26%、27.79%、9.36%和17.69%。工况①-⑤截面位置处管片相对位移与地表沉降变化规律一致,相对位移值的增大速率处于放缓的趋势。
而在同一工况下,左侧拱腰的相对位移略大于右侧拱腰的相对位移,均与之前的结果相符,即拱底位移大于拱顶,盾构进侧位移略大于出侧的。
工况①-⑤沉降值均满足《盾构法隧道施工及验收规范》(GB 50446—2017)[17]中规定的隧道结构沉降变形控制指标。

图10 工况①-⑤时所取截面管片相对位移曲线Fig.10 Relative displacement curves of slices in the section taken under working conditions I-V
4.1.3 管片内力分析
工况①-⑤时既有隧道内力变化曲线如图11所示。由图可知,在盾构机开挖过程中,衬砌会变为扁鸭蛋形状。轴力变化情况呈现出先增大后减小的规律,且轴力值大小随着净距D的增加而不断减小。轴力值从kw-11阶段开始迅速增大,此时盾构机掌子面处于既有隧道轴线下方;在kw-21-kw-26阶段时出现轴力的最大值。待盾构机驶出后,轴力值得以恢复,但仍比未开挖阶段大。在kw-21阶段,工况①-⑤的最大轴力值分别减小了5.13%、3.16%、5.39%、8.09%。
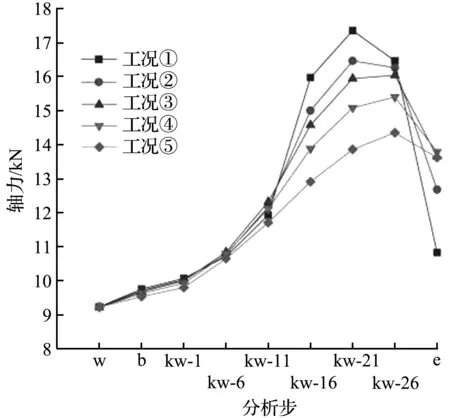
(a) 轴力曲线

(b) 弯矩曲线
弯矩的变化规律基本与轴力吻合,最大弯矩仍然发生在kw-21至kw-26阶段。在kw-21阶段,工况①-⑤既有隧道弯矩分别递减了17.44%、11.99%、18.46%、29.61%。且既有隧道内力的衰减趋势随着净距的增大逐渐减小。
从图11可知,随着2条隧道净距的增大,既有隧道附加内力减小,当掌子面距离前方既有隧道轴线2.0D左右时,附加内力开始显著增大。当掌子面推进到距离后方既有隧道轴线2.0D时,既有隧道的附加内力逐渐减小。分析其原因,随着新建隧道的不断开挖,既有隧道受到盾构掘进正面推力和底部土体卸载的影响不断增大,附加内力随之增大,而盾构机逐渐驶出后,顶推力得以消散,附加内力逐渐减小。但在kw-21-kw-26阶段时,由于2条隧道净距的增大,顶推力所产生的影响小于底部土体卸载的影响,所以工况①、②的内力呈现出减小趋势,而工况③-⑤呈现出增大趋势。
4.2 深埋条件下新建隧道下穿既有隧道施工影响分析
为了探究深埋条件下新建盾构隧道下穿既有隧道施工时,2条隧道间净距改变对既有隧道的影响,分析净距分别为0.5D、1.0D、1.5D、2.0D、3.0D时的位移与内力情况。
4.2.1 地表沉降分析
工况⑥-⑩既有隧道地表竖向沉降曲线如图12所示。从图中可知,当既有隧道属于深埋隧道时,下穿产生的竖向沉降会随着净距的增大而增大。其原因为,当施工开挖使得地下土体卸载,由于土体孔隙率较大,因此导致既有隧道在该处发生土体压缩;随着净距的增大,土体自重也在不断增大,进而加剧土体沉降。

图12 工况⑥-⑩既有隧道地表竖向沉降曲线Fig.12 Vertical settlement curves of the existing tunnel surface of working conditions VI-X
工况⑥-⑨,2条隧道轴线交叉位置处沉降,即最大沉降值处,分别增大了10.70%、5.30%、4.46%;当工况⑦、⑨和⑩时,沉降值相继增大了9.99%和6.52%,表明虽然土体为软土,但仍具有一定承载力,沉降增长率并不会无限增大,也在逐渐减缓。
工况⑥-⑩新建隧道地表竖向沉降曲线如图13所示。当盾构隧道下穿深埋既有隧道时,最小沉降值出现在既有隧道下方,且随着净距的增大缓慢增大,工况⑥-⑨分别增大了10.70%、5.30%、4.46%,增长率逐渐减小。在掘进过程中,入口部分沉降仍然比出口部分大,入口的沉降值随着净距的增加逐渐增大。分析认为,由于新建隧道开挖导致底部土体支撑作用消散,因此产生软土层压缩变形。

图13 工况⑥-⑩新建隧道地表竖向沉降曲线Fig.13 Vertical settlement curves of the new tunnel surface of working conditions VI-X
4.2.2 管片位移分析
所取截面(y=30 m)的工况⑥-⑩时所取截面管片相对位移曲线如图14所示,由图可知衬砌管片仍为左、右内凹,向下外凸的扁鸭蛋形状。同样印证了盾构入口处位移大于出口处,但最大位移却发生在拱底位置。

图14 工况⑥-⑩时所取截面管片相对位移曲线Fig.14 Relative displacement curves of existing tunnel slices taken at the working conditions VI-X
从图14中还可以看出,管片整体最大位移发生在拱底,最小位移发生在拱顶,且整体最大位移变化量随净距的增大而逐渐减小。而左侧拱腰的位移值,在净距为0.5D、1.0D、1.5D时,比右侧拱腰的位移值分别高出0.04、0.02、0.01 mm,呈现出随着净距的递增,盾构掘进过程对既有隧道两侧的影响逐渐减弱的特征。深埋工况⑥-⑩沉降值也同样满足规范[17]中的规定。
4.2.3 管片内力分析
工况⑥-⑩时既有隧道内力变化曲线如图15所示。由图可见,内力变化情况展现出先增后减的规律,在前期阶段数值几乎相差无几,推断在kw-6阶段以前,盾构开挖掘进过程对既有隧道的内力影响可以忽略不计,而此时掌子面所处位置在既有隧道轴线前方2.0D,约12 m处。越过轴线位置处2.0D时,内力值开始减小。总体的趋势显示出随净距增大影响逐渐减弱。
在kw-11阶段,内力值开始迅速增大,且随着净距的增加而逐渐减小,在kw-21-kw-26阶段时达到最大值。究其原因,主要为既有隧道底部土体卸载,软弱土体受到扰动产生附加内力,随着净距的增大,土体受到的扰动减弱,导致附加内力值降低。

(a) 轴力曲线

(b) 弯矩曲线
5 结论
本文以上海地铁15号线下穿运营9号线桂林站区间工程为研究对象,通过有限元模拟和工程实测数据对比的方法,基于MCC模型来考虑土体非线性对不同埋深、不同净距情况下,新建盾构隧道动态开挖对既有隧道的影响规律,得出如下主要结论:
① 在软土地质里,由于土体压缩性大,会在自重条件下产生土体压缩,导致沉降值逐渐增大,因此既有隧道所处位置的地表竖向沉降不会随相对距离的增大而逐渐减小,与在正常土层中的规律不同,应在工程实际中重点考虑。此外,新建盾构入、出口一侧的变形差异,在浅埋隧道时更为明显。
② 既有隧道的管片变形在数值上满足规范要求,既有隧道的埋深不同时管片最大变形出现的位置一致,均出现在既有隧道拱底位置处,且随着净距的增大,管片变形的影响开始趋弱。
③ 盾构掘进过程中既有隧道的内力值,当既有隧道轴线位于盾构掌子面前方约2.0D,盾构机尚未到达既有隧道轴线下方时,对内力值的影响微乎其微。穿越过既有隧道轴线2.0D后,内力影响开始减弱,主要影响范围为[-2.0D, 2.0D]。净距增大会使既有隧道内力值进一步减小,意味着新建盾构隧道开挖对既有隧道的影响逐渐减小。
④ 通过实测数据分析,验证了数值模拟所得结论的正确性:掌子面距离既有隧道轴线距离大于2.0D时,开挖带来的土体扰动对既有隧道管片结构的影响较为微弱;在推进过程中既有隧道的结构沉降方面,能够较好验证数值模拟所得出的结论,即对管片结构的显著影响区间范围为[-2.0D, 2.0D]。

