Gb-(p,r)-E-半预不变凸多目标规划的最优性条件
祁钰, 高晓艳
(西安科技大学 理学院, 陕西 西安 710600)
0 引言
从20世纪70年代以来,人们对多目标规划的探索研究给予了极大的关注和重视。到目前为止,各种凸函数及其推广在多目标规划中也得到了广泛应用。许多学者在这方面进行了研究。
1981年,Hanson[1]首次引入了不变凸函数。接着,许多研究学者对不变凸函数进行了推广,定义了(p,r)-ρ-(η,θ)-不变凸函数、B-(p,r,α)-不变凸函数,并分别研究了相应的多目标分式规划、广义分式规划、多目标规划等问题的最优性条件以及相应的Wolfe对偶模型的对偶问题[2-5]。
1999年,Youness[6]推广了凸函数,首次提出了E-凸集和E-凸函数;2006年,覃义等[7]指出了文献[6]的错误所在并予以了调整更正;之后半E-预不变凸函数被提出[8];文献[9-13]定义了不同的广义凸函数,并对其性质、对偶性以及最优性条件等进行了研究。
2009年,Antczak[14-15]定义了G-不变凸函数,并证明了多目标规划问题的最优性条件和若干对偶定理;之后关于G-不变凸函数的推广日渐出现,G-V-不变凸函数、(G-V,ρ)-不变凸函数被科学地定义,并证明了有关最优性条件及对偶结果[16-19]。2022年,江柳等[20]提出了G-B-(p,r,α)-不变凸函数,讨论了多目标规划问题的几个最优性条件。
本文在文献[13,20]的基础上,给出了Gb-(p,r)-E-半预不变凸函数的概念,根据所提出的定义,研究了相关多目标规划问题,并证明了几个最优性条件。
1 预备知识及函数定义
首先,引入以下几个符号:
在n维实向量空间Rn中,对于x=(x1,x2,…,xn),y=(y1,y2,…,yn)∈Rn,有以下定义:
①x=y⟺xi=yi,i=1,2,…,n,
②x>y⟺xi>yi,i=1,2,…,n,
③x≧y⟺xi≧yi,i=1,2,…,n,
④x≥y⟺xi≧yi,i=1,2,…,n,但至少存在一个k∈{1,2,…,n},使得xk>yk,即x≠y。
下面回顾一些相关知识。
定义1[20]设X⊂Rn是非空子集,若存在η:X×X×[0,1]→Rn{0},α:X×X→R{0},E:X→X,使得对于∀x,y∈X,∀λ∈[0,1]有
E(y)+λα(E(x),E(y))η(E(x),E(y),λ)∈X,
则称X是关于η和α的α-E-半不变凸集。
定义2[20]设X⊂Rn是α-E-半不变凸集,函数f:X→R,如果存在η:X×X×[0,1]→Rn{0},α:X×X→R{0},对于∀x,y∈X(E(x)≠E(y)),∀λ∈[0,1]有
f(E(y)+λα(E(x),E(y))η(E(x),E(y),λ))≤(<)λf(E(x))+(1-λ)f(E(y)),



定义4称函数f=(f1,f2,…,fq):X→Rq在α-E-半不变凸集X上是局部Lipschitz的,若存在一个正数k和x的邻域N(x),对∀x,y∈X,有
|f(E(x))-f(E(y))|≤k‖E(x)-E(y)‖。
如果f=(f1,f2,…,fq):X→Rq是局部Lipschitz的,则函数f在E(x)处沿方向E(d)的Clark广义方向导数和Clark广义梯度分别定义为
∂f(E(x))={ξ∈Rn|〈ξ,E(d)〉≤f0(E(x);E(d)),∀d∈Rn}。
基于α-E-半预不变凸函数和G-B-(p,r,α)-不变凸函数,本文定义了一类新的广义凸函数。
本文均假设X⊂Rn是一个非空α-E-半不变凸集,f=(f1,f2,…,fq):X→Rq,fi(i=1,2,…,q)是定义在X上的局部Lipschitz函数,Ifi(x)为fi的值,p、r是任意实数,G=(Gf1,Gf2,…,Gfq):R→Rq,Gfi:Ifi(x)→R是严格单调递增的可微实值函数,有向量函数η,θ:X×X→Rn,函数bi:X×X→R+和常数
记I=(1,1,…,1)T∈Rn。
定义5如果存在函数G:R→Rq,向量函数η,θ:X×X→Rn,函数bi:X×X→R+和常数
使得对∀x∈X,有

定义6如果存在函数G:R→Rq,向量函数η,θ:X×X→Rn,函数bi:X×X→R+和常数
使得对∀x∈X,有


定义7如果存在函数G:R→Rq,向量函数η,θ:X×X→Rn,函数bi:X×X→R+和常数
使得对∀x∈X,有

注1相较于Gb-(p,r)-E-半预不变凸函数的定义,Gb-(p,r)-E-半预不变凹函数的定义应将定义5中的不等式换为
注2接下来将在p≠0,r≠0的情况下进行证明,其他情况下的证明与之类似。
2 最优性条件
将研究α-E-半预不变凸多目标规划问题(VP):
其中E:X→X,且X⊂Rn是关于η和α的α-E-半不变凸集:
且fi、gj、ht是X上的局部Lipschitz函数。 (VP)的可行域记为
X0={x∈X|g(E(x))≦0,h(E(x))=0}。
用
表示对应的拉格朗日乘子分别为正、负的等式约束指标集。
定义8设x0∈X0,如果不存在x∈X0,使得f(x) 本节将研究涉及Gb-(p,r)-E-半预不变凸函数的多目标规划问题的最优性条件。 ① 存在λ=(λ1,λ2,…,λq)>0,μ=(μ1,μ2,…,μm)≧0使得: i=1,2,…,q,因函数Gfi:Ifi(x)→R是严格单调递增可微实值函数,则 所以 (1) 结合式(1)可得 又λi>0,所以 (2) 有 因为μ=(μ1,…,μm)≧0,所以 所以 又μj≧0,得 (3) 那么对任意t∈T,都有 因为h(E(x))=0,所以 再将所得l个式子相加得 (4) 将式(2)、(3)、(4)相加得 由条件a)知,存在 使得 ① 存在λ=(λ1,λ2,…,λq)>0,μ=(μ1,μ2,…,μm)≧0使得: 证明由定理1知 又因为λi>0,所以 (5) 由定理1知, 函数gj是非可微Gb-(p,r)-E-半预不变拟凸函数,所以 因为μj≧0,得 (6) 由定理1知, (7) 将式(5)、(6)、(7)相加得 由条件a)知,存在 使得 本文介绍了Gb-(p,r)-E-半预不变凸函数,它是α-E-半预不变凸函数和G-B-(p,r,α)-不变凸函数定义的推广。除此之外,还研究了一类多目标规划问题,这些问题涉及本文所介绍的Gb-(p,r)-E-半预不变凸函数,并证明了其可行解是弱有效解的若干最优性结果。之后,还将继续研究多目标规划问题的对偶模型,证明其对偶定理等。


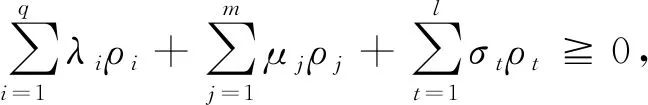


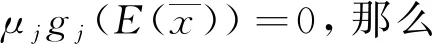


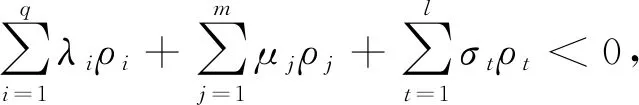






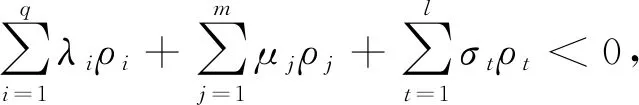
3 总结

