气液固流化床气泡特性及气含率预测模型

王 超，钱 冬，张 琳，丁红兵

气液固流化床气泡特性及气含率预测模型

王 超1, 2，钱 冬1, 2，张 琳1，丁红兵1, 2

(1. 天津大学电气自动化与信息工程学院，天津 300072；2. 天津市过程检测与控制重点实验室，天津 300072)

气含率及气泡直径会直接影响流化床内的反应进程及传质效率，为更好地认识局部流动结构，径向气含率及气泡直径分布成为重点研究内容，特别是径向气含率预测模型的建立具有重要意义．已有平均气含率预测模型都有各自的适用范围，对不同实验体系的应用会表现出局限性．针对以上问题，本文结合电导探针测量法与流体仿真技术，以直径为100mm和高度为1.5m的气液固流化床为研究对象，系统地研究了在气相表观速度为0.014～0.283m/s、液相表观速度为0.007～0.028m/s、液相黏度为1～40mPa·s、液相表面张力为0.053～0.072N/m及固相体积分数为0～30%条件下径向气含率及气泡直径分布特征．结合本实验系统及相关研究数据，提出一种适用于气液固系统的平均气含率预测模型．基于此预测模型，进一步考虑气相表观速度及表面张力对径向气含率分布的影响，采用粒子群优化算法建立气液两相体系的径向气含率预测模型．结果表明：两相及三相体系平均气含率预测模型充分考虑了气液相表观速度、液相物性、固相物性及管径对平均气含率的影响，相比现有经典平均气含率预测模型，拓宽了适用范围并提高预测精度，其平均绝对百分比误差(mean absolute percentage error，MAPE)分别为17.14%和18.36%，超出90%数据点的相对误差在±30%之内．径向气含率预测模型对靠近管道中心处的气含率预测更加准确，其MAPE可达到12.26%．以上预测模型的建立对理解管内全局及局部传质问题、流化床反应器设计都具有指导意义．

气液固流化床；径向气含率；径向气泡直径；气含率预测模型

在科学技术飞速发展的过程中，气液两相流和气液固多相流在越来越多的领域里占据着重要地位．流化床作为一种多相流系统，具备构造简单、操作便捷等优势，被广泛应用于化工、制药、石油等领域[1-4]．流化床中通常采用小颗粒来增加两相之间的接触面积，从而提高热稳定性和传热传质效率[5]．流化床反应器一直是一个主要的研究对象，但由于相关流体动力学对流体物理特性、操作条件和几何设置非常敏感，其设计、放大和预测仍是具有挑战性的问题，因此需要进一步研究．

气含率和气泡直径是流化床的重要设计参数，能够直接反映流化床体系内的流动特性，同时也是表征气液相界面积的关键参数，可直接影响流化床内部的传质效率[6]．随着实际生产过程中需求的提高及测量技术的迅猛发展，径向气含率及气泡直径分布受到越来越多的关注，获取气含率及气泡直径的局部信息有助于更好地理解流化床的内部流动结构．王祖恒[7]采用电导探针对旋转曝气器中径向及轴向气含率的分布进行研究，考察体系内的充氧均匀性．卢霞[8]采用粒子图像测速和数值模拟方法研究外环流氨化反应器的径向气含率及气泡直径分布，通过分析气液传质面积和效率来指导反应器的设计．但在不同反应器内及不同操作条件下，径向气含率和气泡直径并不呈现统一的分布状态．Ohnuki等[9]通过改变气速和液速对DN200的实验管道进行研究，表明气含率在径向方向上呈现两种常见状态，即边壁峰与中心峰．Tomiyama等[10]对气含率分布的机理进行分析，发现其可能出现边壁双峰形式．Raimundo等[11]对不同气泡柱尺寸下的气泡特性进行实验研究，发现在不同气速下径向气含率与气泡直径呈现中心峰状态．艾涛等[12]对气液并流上流式反应器研究发现，气泡直径沿径向先增大后减小．本实验系统属于共流向上气液固流化床，增加径向气含率及气泡直径分布的规律分析，可为今后研究提供一定的数据基础，对该类反应器的设计具有指导意义．

由于气含率及气泡直径受多参数影响，因此在不同实验体系条件下并没有完全统一的规律来对其进行描述．严鹏[13]采用CFD-PBM耦合模型与电阻层析成像技术对不同表面张力及黏度条件下气泡柱中的气泡特性展开研究，黏度和表面张力的增加有利于气泡的聚集汇并，形成大气泡，气含率降低．Orlando等[14]采用实验测量的方法展开研究，结果表明表面活性剂降低表面张力后，气泡直径减小但气含率增加，同时气速促进气含率升高．周秀红[6]采用CFD-PBM耦合模型和浸入式在线多相测量仪对气液固循环流化床内操作条件及液相性质对流体动力学参数的影响展开研究．综上，目前对固相体积分数影响气含率及气泡直径的研究较少，实验测量结合数值模拟方法可更好地对多相流展开研究[15]．

气含率的变化趋势和变化程度在不同因素的影响下具有差异性，为更好地理解管内局部流动状态、液体混合及传质传热，建立径向气含率预测模型是一种重要途径，平均气含率的准确预测是上述模型建立的基础．王丽军等[16]全面考虑了气速、管径、液相物性等参数影响，并且将参数无量纲化，给出了气液固浆态床的平均气含率预测模型，但模型主要针对高气速数据进行回归，对0.13m/s以下的小气速数据表现出不适应性，同时未考虑固体粒径及密度对气含率的影响．李蔚玲[17]考察了颗粒及液相物性对平均气含率的影响，基于无量纲参数建立了平均气含率预测模型，但模型未考虑液相表面张力的影响，且将固相体积分数直接引入模型中，致使模型不适用于固体为0的极端情况，应用具有局限性．Götz等[18]考虑气相、液相及固相多种因素建立了平均气含率预测模型，但只适用于气速小于0.1m/s的情况，使用范围具有局限性．Islam等[19]对气液固系统建立气含率预测模型，但未考虑固相体积分数对气含率的影响，引入的无量纲参数中包含了基于气泡直径的雷诺数b，然而在实际情况下，对气含率进行预测时很难清楚各条件的气泡直径，因此模型不易推广且应用受限．以往的研究中，在构建平均气含率预测模型时，由于参数考虑得不够全面，参数适应范围较小或具有针对性，或选择的无量纲参数具有特殊性致使模型应用受到限制．

不均匀的径向气含率分布是管内多种流动机制相互作用的结果．使用纯经验的数学式归纳气含率的径向分布具有难度且模型的应用容易受到限制.曹长青[20]和Wu等[21]发现径向气含率分布可用二次曲线来表示并考虑操作条件、液相物性等参数的影响建立径向气含率预测模型，但前者直接将气速、黏度等参数引入模型，致使模型参数过多且不易推广，后者选用无量纲量表征各参数的影响，但回归所用数据基本为纯水体系内的局部气含率．

针对上述问题，本文结合电导探针测量技术与CFD-PBM耦合模型，考虑气相表观速度、液相黏度及表面张力和固相体积分数，对气液固三相流化床系统的径向气含率及气泡直径分布规律展开研究．结合本实验系统和相关文献[22-30]的平均气含率数据，提出新的平均气含率预测模型，该模型考虑参数较全面且适用范围较广，并与经典预测模型进行比较分析，在一定参数范围内表现出更好的预测效果．以上述模型为基础，考虑气速及表面张力进一步建立了无量纲化的径向气含率预测模型．

1 数学模型

1.1 CFD-PBM耦合模型

构建三相流动模型(欧拉-欧拉-欧拉模型)，液相被视为连续相，气相和固相被视为离散相，利用颗粒动理学模型对分散的固体压力和黏度进行建模．欧拉模型需要相间作用力来进行封闭，其中最重要的为曳力模型和升力模型[31]．气液、气固及液固间曳力模型选择为Tomiyama(PBM-customized)模型、Schiller-Naumann(PBM-customized)模型及Schiller-Naumann (PBM-customized)模型．气液和液固之间升力选择为Tomiyama模型和Moraga模型．其中质量守恒方程为

式中：下标代表气相(g)、液相(l)及固相(s)；、和分别表示各项的体积分数、密度和速度．

动量守恒方程为

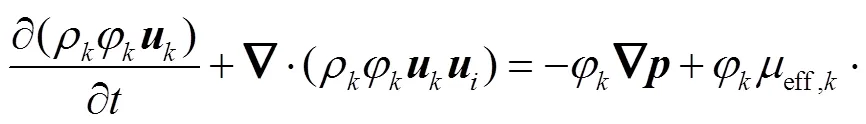
式中：下标代表气相(g)或液相(l)；等号右边分别为压力梯度、应力、重力和气液间动量交换作用力．

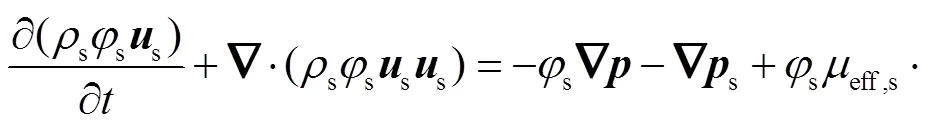
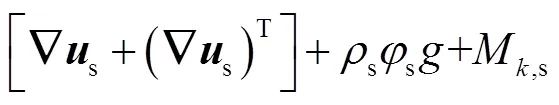
式中：下标s代表固相；等号右边分别为压力梯度、由于颗粒碰撞的附加压力、应力、重力、气相或液相与固相间动量交换作用力．

群体平衡模型(population balance model，PBM)在空间和时间上描述了气泡的聚并和破碎现象，是描述反应器中气泡或颗粒大小分布的一种方法．本文选用被广泛使用的Luo聚并模型[32]，该模型将气泡合并分为气泡与气泡碰撞、碰撞时两气泡的速度能否引起气泡合并两部分．Zhou等[31]通过对比Luo和Lehr分别提出的破碎模型，表明Lehr修正后的模型对于流化床内流动更为适用，本文选用Lehr模型作为破碎模型．PBM模型的基本守恒方程为

1.2 求解方法

采用非稳态分离求解器对模型方程进行求解．液相设置为主相，气相和固相为次相．气相和液相从反应器底部进入，以速度入口作为入口边界条件，分别给定了气体和液体的初始入口速度，对加入的固相体积分数进行初始化设置．出口处设为压力出口条件，边壁处设为无滑移边界．在PBM模型中，通过离散求解方法将气泡尺寸分为16段，定义气泡最小直径为2mm，气泡增长比例V＋1/V＝1.26，气泡最大直径为64mm，包含实验中气泡尺寸范围，进入床层的所有气泡初始直径为位于第9段的8mm．

大量实验[20,33]表明流化床的时均流体力学行为是平稳的和轴对称的，不同研究人员[34-35]比较了二维和三维模拟，发现三维瞬态模拟的时间平均结果与二维轴对称稳态模拟相似．为节省计算资源，采用二维模拟方法，划分网格尺寸且边界进行加密处理，考虑网格精度选择合适的网格数量进行模拟，其他仿真设置如表1所示．

表1 其他仿真设置

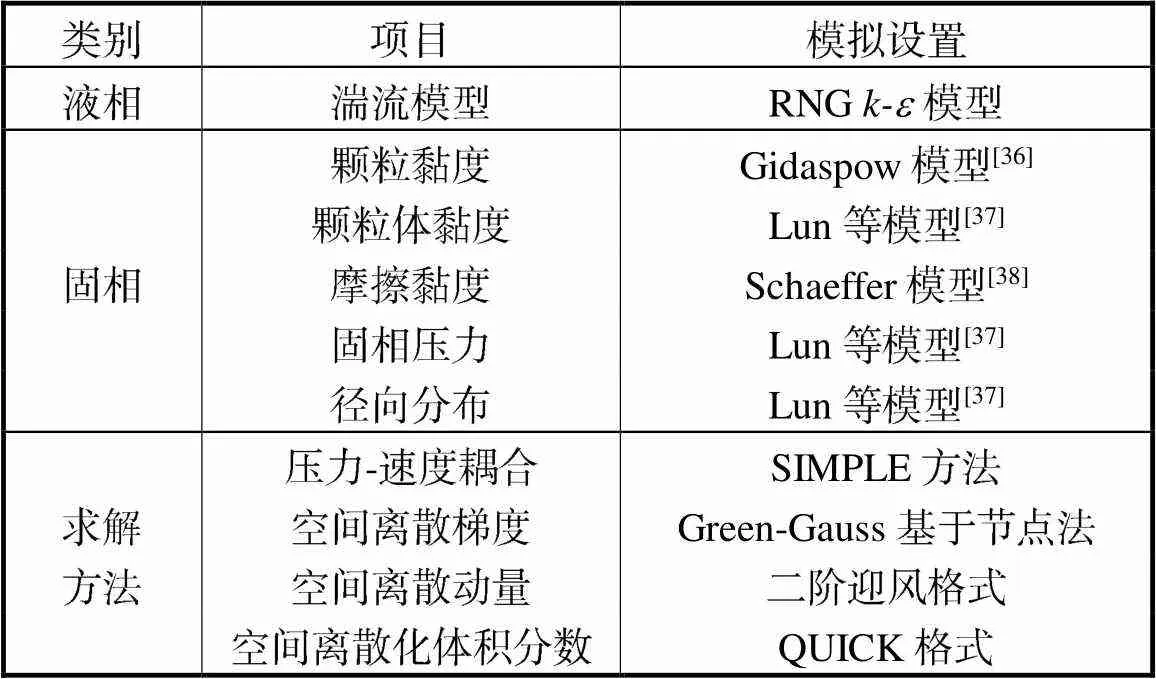
Tab.1 Other simulation settings

2 实验设计

2.1 实验装置

如图1所示，气液固三相流化床装置的管道内径为100mm，床高为1500mm，装置主要分为供水系统、供气系统和反应器系统3个部分．实验中的气相和液相分别为空气和水，固相为平均粒径p＝250μm和密度p＝3500kg/m3的氧化铝．气相及液相流量范围分别为0～10m3/h和100～1000L/h，待分布器均匀分布后进入实验段，固相在实验开始之初从反应器上端加入到管段中．出口处气相经气液分离后自由逸出，液相由循环回路返回到循环水槽中，固体颗粒在液体和气体作用下呈现流化状态，最后自动沉降到流化区．

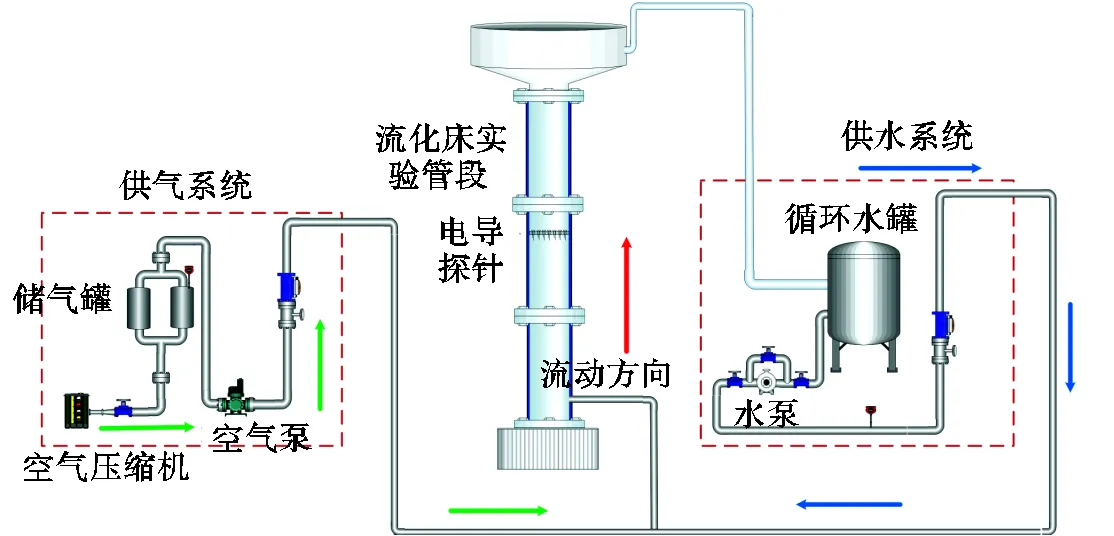
图1 气液固三相流化床实验装置

2.2 电导探针测量法

实验采用七通道双头电导探针阵列对流化床内部径向气含率及气泡直径进行测量，每组探头到管道中心距离与管道半径的比值()从左到右分别为-0.75、-0.50、-0.25、0、0.25、0.50和0.75，采样时间为100s，采样频率为15kHz，将电导探针阵列安装于高875mm处，在充分发展区系统流动特征较为稳定，高度对流动状态影响不大[39]，传感器布局如图2所示．

图2 传感器布局

电导探针测量原理是基于探针处于不同介质中的电导率差异来对不同相进行区分，进而获得气含率等参数．选用自调整双阈值算法对信号进行处理，输出信号如图3所示．

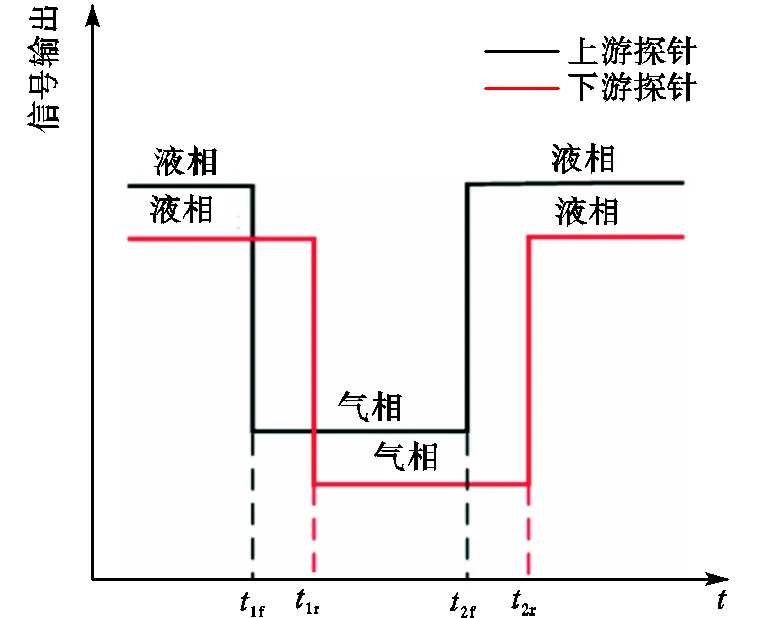
图3 传感器输出信号

采样时间内低电平所占时间百分比表示此处气含率，即

采用相关测速法对上下游信号进行处理，得到气泡平均速度b，结合气泡经过探针的时间间隔(2f－1f)得到气泡直径b．在多气泡体系中，一般采用Sauter平均直径(32)作为气泡的平均尺寸，即

式中：bi为第个气泡的直径；n为直径为bi的气泡个数．

3 气泡特性规律分析

3.1 CFD-PBM耦合模型数值模拟验证

在气液固三相流动体系中，径向气含率的实验及数值模拟结果如图4所示．在液相表观速度l为0.014m/s、气相表观速度g为0.021～0.142m/s、固相体积分数V为10%条件下，该模型的数值模拟结果与实验数据趋势一致且数值吻合，表明该模型能够较好地描述和预测气液固三相流化体系．

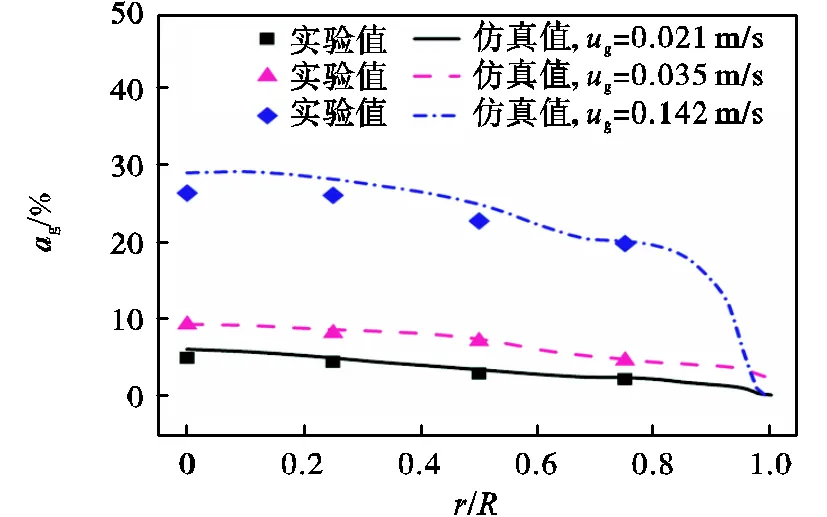
图4　　气液固三相流动体系径向气含率实验与仿真结果对比(u1＝0.014m/s，CV＝10%)

3.2 径向气含率分布

不同气相表观速度g、液相黏度l及表面张力l、固相体积分数V对径向气含率分布特性的影响如图5所示，气含率在径向方向上呈现中心峰状态和不均匀结构．由图5(a)可知，在气相表观速度增加过程中，整体气含率增加，中心位置处模拟得到的气含率由6.30%逐渐增加到44.27%，同时径向气含率分布曲线逐渐陡峭．由图5(b)和(c)可知，气含率与液相黏度及表面张力的变化呈现负相关关系．伴随表面张力增大，大气泡占据主要地位，其上升过程中速度普遍高于小气泡，因此大气泡停滞在某一位置的时间较短致使气含率降低．当固相加入后，随着固相体积分数增加，由于颗粒相的阻碍作用，气含率呈现下降趋势．由气液两相向气液固三相转变时，气含率降低趋势较为明显，如图5(d)所示．

3.3 径向气泡直径分布

图6所示为不同气相表观速度g、液相黏度l及表面张力l、固相体积分数V对径向气泡直径分布特性的影响，气泡直径沿径向呈现减小趋势．由图6(a)结果可知，随着g的增加，气泡直径32随之变大，中心位置处的模拟气泡直径由3.85mm增加到6.74mm．较大气相表观速度会提高气泡之间聚并的概率，促使大气泡产生．此外，气泡直径在靠近管道中间部分的径向减小趋势缓慢，到＝0.7～0.9位置处开始出现显著的降低趋势，这表明在管道中间基本上以较大的气泡形式存在．图6中实验与仿真的对比结果显示，该数值模型对径向气泡直径分布表现出了较好的预测性．

图5 径向气含率的分布特性

图6(b)和(c)结果表明，气泡直径与液相黏度及表面张力呈正相关关系．黏度及表面张力增加时，气泡的聚并概率加大，气泡更容易汇聚形成大气泡．随着固相含量增加，径向气泡直径呈现整体的增大趋势．这是由于固体颗粒能够促进气泡聚并，固相含量越高，气泡的聚并现象越明显，整体呈现中心区域的气泡直径大于边壁区域的现象，结果如图6(d)所示．

图6 径向气泡直径的分布特性

4 气含率预测模型

4.1 平均气含率预测模型

对气液或气液固体系中的平均气含率预测已有不少研究，但存在选用参数不全面或使用范围较窄等问题，本文选用当前实验系统及相关文献中的平均气含率数据，如表2所示，构建多参数较广范围的数据集．基于无量纲分析提出一种新的气液两相平均气含率预测模型，并以此为基本模型，考虑固相性质等参数提出新的气液固三相平均气含率预测模型，为径向气含率预测模型的建立打下基础．发展的预测模型适用于大气压环境，所用参数范围：气相表观速度g为0.01～0.45m/s、液相表观速度l为0～0.028m/s、液相黏度l为1～40mPa·s、液相表面张力l为0.027～0.073N/m、固体密度p为2440～3500kg/m3、固体粒径p为35～250μm、固相体积分数V为0～35%、管径为80～280mm．

本文分析了径向气含率随参数改变时的变化规律，基于径向气含率可以计算得到截面平均气含率为

4.1.1 气液两相系统

对气液两相体系，全面考虑气相及液相表观速度、液相黏度及表面张力、管道内径对平均气含率的影响，构建平均气含率预测模型．

采用修正气相弗劳德数g代表气相表观速度及管道内径的影响，气相表观速度是影响气含率的一个重要因素，管道内径大于0.15m时，平均气含率几乎不受影响，采用特征长度c来表征不同管径的影响对g进行修正[19]，即

其中

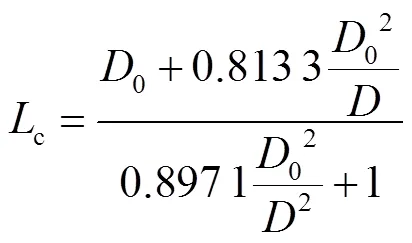
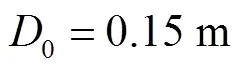
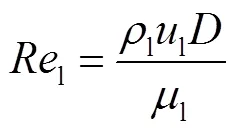
式中l为液体密度．

表2 预测模型的数据集

Tab.2 Datasets of the prediction model

综上，平均气含率预测模型的参数化表达为

选用表2所示数据集中气液两相体系对应的237个平均气含率数据点，采用最小二乘法对式(11)进行非线性回归分析，得到的模型参数为1＝0.8075，2＝0.2722，3＝0.2651，4＝1.2185，5＝-1.93×10-4．预测效果如图7所示，拟合优度2为0.9168，相对均方根误差rRMSE为20.4%，平均绝对百分比误差MAPE为17.14%，其中92%的数据点相对误差在±30%以内，该模型具有较好的预测效果．

图7 气液两相模型的预测效果

4.1.2 气液固三相系统

对气液固三相体系，悬浮在液相中的固体会降低气含率，以上述两相模型为基础，考虑固体颗粒性质(颗粒粒径p及密度p)和体积分数V的影响并以指数形式引入，建立三相平均气含率预测模型

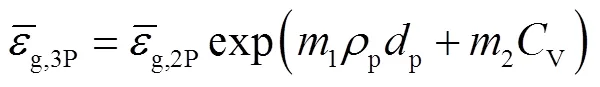
选用表2所示数据集中气液固三相体系对应的88个平均气含率数据点，采用最小二乘法对式(12)进行非线性回归分析，得到的模型参数为1＝-0.1228，2＝-2.1336．预测效果如图8所示，拟合优度2为0.8370，相对均方根误差rRMSE为21.9%，平均绝对百分比误差MAPE为18.36%，其中91%的数据点相对误差在±30%以内，该模型具有较准确的预测效果．

4.1.3 模型评价

表3总结了气液两相系统以及气液固三相系统的经典平均气含率预测模型，选用表2数据集中气液两相及气液固三相平均气含率数据对表3中的模型进行评定并与本文模型进行比较分析，引入MAPE和均方根误差RMSE作为评价指标，模型评定结果如表4所示，以此说明本文模型的优势所在．

结合表3和表4结果可知，对于气液两相体系，Hikita等[40]和Elgozali等[41]建立的预测模型适用于较窄的液相黏度范围，对超出17.8mPa·s和25.6mPa·s液相黏度的系统已不能较好预测，其中后者适用的气相表观速度范围较窄，对超出气速为0.085m/s的系统已不适用．Götz等[18]建立的模型适用气相表观速度范围较窄，对超出0.10m/s气速的气含率预测表现出不适用性．对于气液固三相体系，Begovich等[42]建立的预测模型在固相性质方面只考虑了固相粒径及密度因素，未考虑固相体积分数对气含率的影响，当固相体积分数变化时，模型预测的气含率都为相同值，致使预测结果出现较大偏差，考虑的气相表观速度、黏度及表面张力范围都要窄于本文模型，且该模型并不适用于液相速度为0的情况．Götz等[18]建立的模型考虑固相物性参数比较全面，但仍存在适用气速范围较小的问题，使用气泡直径参数B,ref为2mm作为参比直径，致使模型受限于气速小于0.10m/s的均质流型中．针对表2数据集中相同的平均气含率数据，本文建立的模型在考虑参数全面、参数适用范围较广、模型形式的适用性及预测精度上体现更多的优势．

4.2 径向气含率预测模型

由于流化床内气液流动过程的复杂性，对管道内径向气含率分布规律还难以从理论上进行准确预测，Wu等[21]指出管道内径向气含率分布满足的经验模型，即

表3 气液及气液固系统的经典平均气含率预测模型

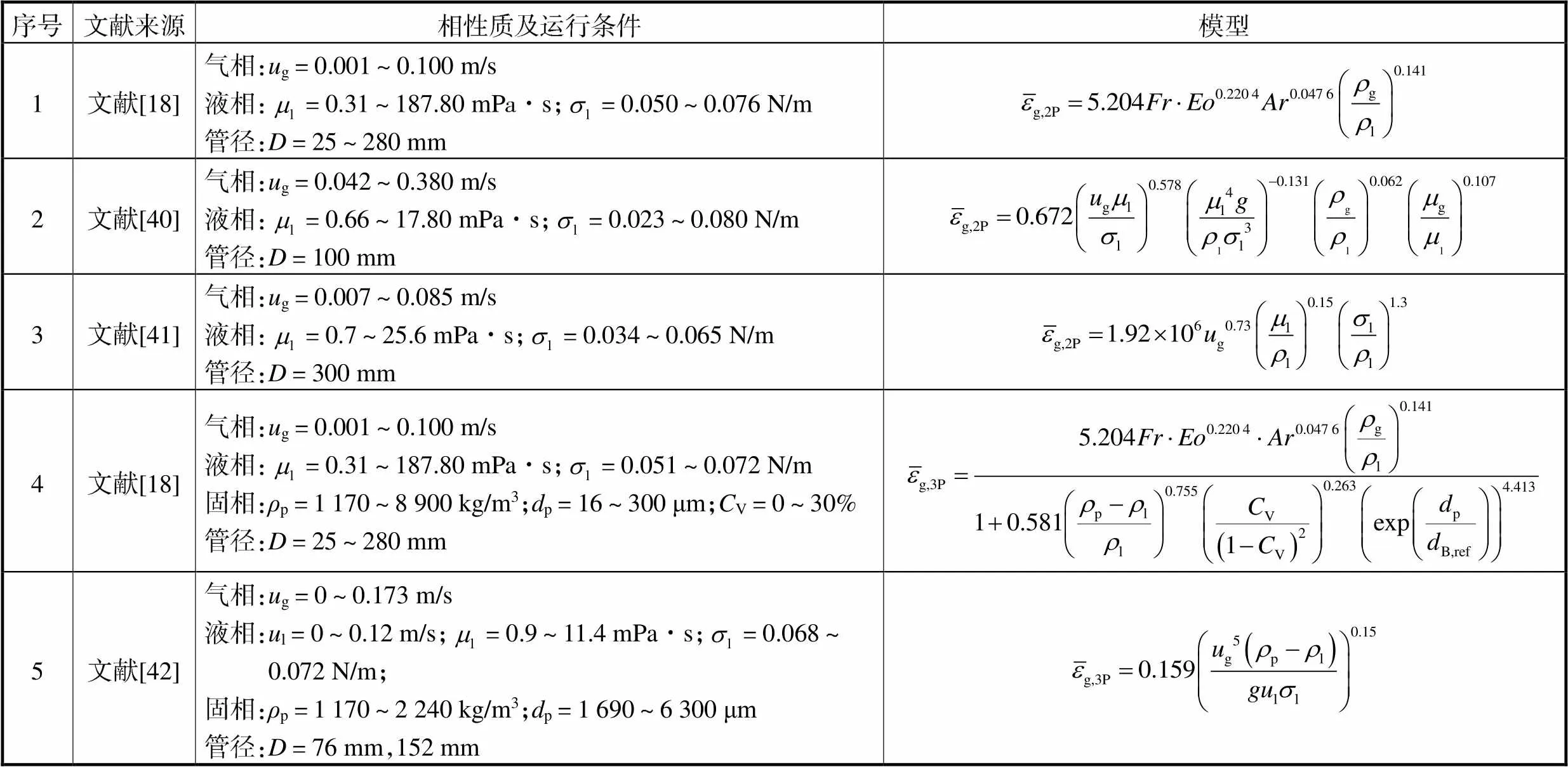
Tab.3 Classical average gas holdup prediction model of the gas-liquid and gas-liquid-solid systems

表4 不同模型的评定结果

Tab.4 Evaluation results of different models

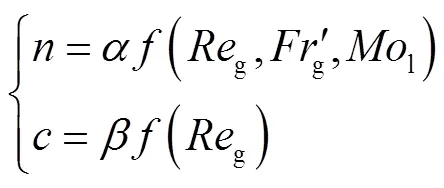
径向气含率分布会受到气相表观速度以及液相性质等多种因素的影响．以式(11)建立的气液两相平均气含率预测模型为基础，考虑气相表观速度在0.035～0.283m/s以及表面张力在0.053～0.072N/m范围内，对径向位置＝0～0.85范围内的局部气含率建立预测模型，回归模型所用的径向气含率数据为本文数值模拟得到的结果．由于目标模型具有较强的非线性关系，基于最小二乘原理的非线性回归已不能较好地求解模型参数，故采用粒子群优化(particle swarm optimization，PSO)算法[43]对模型进行求解，求解流程如图9所示，求解的模型参数分别为

粒子适应度值的计算式为

图9 PSO求解模型参数的流程

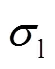
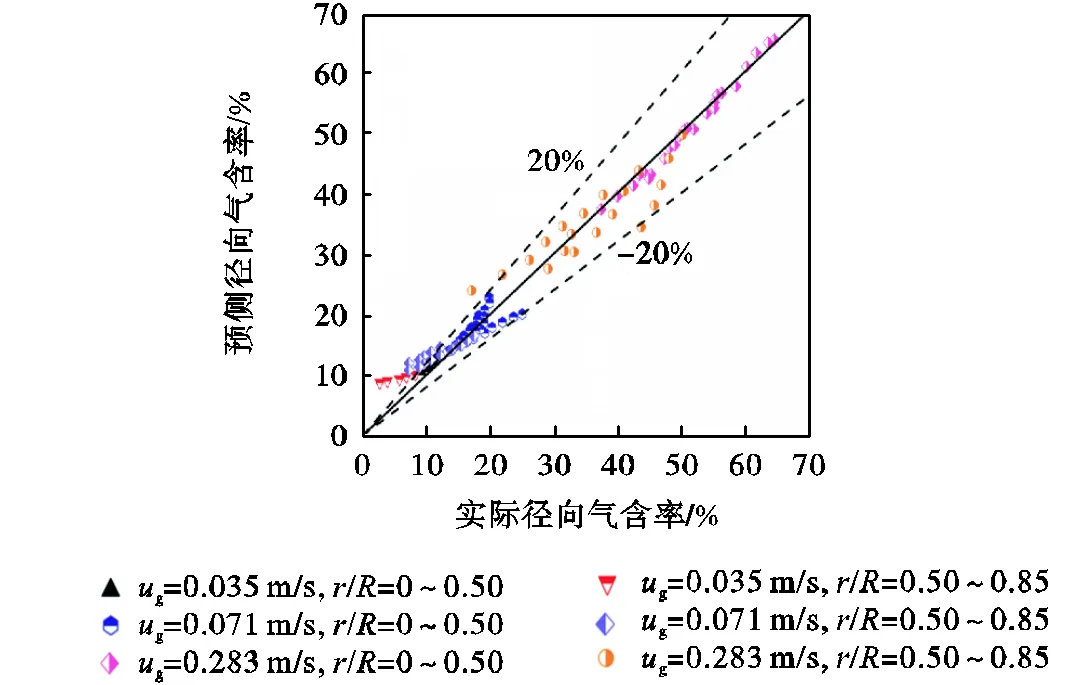
图10 径向气含率模型的预测效果

图11 径向气含率模型的预测效果(ug＝0.283m/s)

5 结 论

结合七通道双头电导探针阵列和CFD-PBM耦合模型考察操作参数、液相物性及固相体积分数对径向气含率与气泡直径分布特性的影响．选用表2数据集中气液及气液固体系的325个平均气含率数据点，提出了新的平均气含率预测模型，以此模型为基础，采用粒子群优化算法建立了径向气含率预测模型．具体结论如下．

(1)径向气含率呈现中心峰分布状态，气含率与气相表观速度呈正相关，与液相黏度、表面张力及固相体积分数呈负相关；气泡直径呈现沿管道中心到边壁的下降趋势，在＝0.7～0.9位置处降低趋势较为明显，气泡直径与气相表观速度、液相黏度及表面张力、固相体积分数均呈正相关．

(2)以修正g、l和无量纲黏度及表面张力共同表征多参数的影响，建立了气液两相平均气含率预测模型，平均绝对百分比误差为17.14%．在此模型基础上，以指数形式引入固相性质的影响建立了气液固三相平均气含率预测模型，平均绝对百分比误差为18.36%，固相体积分数为0并不影响模型使用．与其他经典气含率预测模型相比，本模型在各参数较广范围内可实现更好的预测效果，拓宽了参数适用范围且提高预测精度．

［1］ Fu Z，Zhu J，Barghi S，et al. Minimum fluidization velocity growth due to bed inventory increase in an air dense medium fluidized bed[J]. Chemical Engineering Journal，2019，359：1372-1378.

［2］ Zhang H D，Sun Z N，Zhang M Z，et al. Comparison of the flow structures and regime transitions between a cylindrical fluidized bed and a square fluidized bed[J]. Powder Technology，2020，376：507-516.

［3］ Singh B K，Roy S，Buwa V V. Bubbling/Slugging flow behavior in a cylindrical fluidized bed：ECT measurements and two-fluid simulations[J]. Chemical Engineering Journal，2019，383：123120.

［4］ 谢 悦，梁德乐，朱凯鹏，等. 吸附-光催化流化床降解污染物的研究进展[J]. 科技资讯，2021，19(22)：1-4.

Xie Yue，Liang Dele，Zhu Kaipeng，et al. Research progress on pollutant degradation in adsorption-photocatalytic fluidized bed[J]. Science & Technology Information，2021，19(22)：1-4(in Chinese).

［5］ Zarekar S，Bück A，Jacob M，et al. Numerical study of the hydrodynamics of fluidized beds operated under sub-atmospheric pressure[J]. Chemical Engineering Journal，2019，372：1134-1153.

［6］ 周秀红. 气-液-固循环流化床流动及气-液传质模拟及膨胀床流动实验[D]. 天津：天津大学化工学院，2020.

Zhou Xiuhong. Simulation on Hydrodynamics and Gas-Liquid Mass Transfer in Gas-Liquid-Solid Circulating Fluidized and Experiment in Expanded Bed[D]. Tianjin：School of Chemical Engineering and Technology，Tianjin University，2020(in Chinese).

［7］ 王祖恒. 旋转曝气器的曝气充氧性能及局部气含率研究[D]. 杭州：浙江工业大学化学工程学院，2017.

Wang Zuheng. Study on Aeration Performances and Local Gas Hold-Up Distribution of Rotary Bubble Diffuser[D]. Hangzhou：School of Chemical Engineer-ing，Zhejiang University of Technology，2017(in Chinese).

［8］ 卢 霞. 外环流氨化反应器内气泡流动特性的研究[D]. 武汉：武汉工程大学化工与制药学院，2019.

Lu Xia. Study on Bubble Hydrodynamics Characteristics in an Airlift External Loop Reactor[D]. Wuhan：School of Chemical Engineering and Pharmacy，Wuhan Institute of Technology，2019(in Chinese).

［9］ Ohnuki A，Akimoto H. Experimental study on transition of flow pattern and phase distribution in upward air-water two-phase flow along a large vertical pipe[J]. International Journal of Multiphase Flow，2000，26(3)：367-386.

［10］ Tomiyama A，Tamai H，Zun I，et al. Transverse migration of single bubbles in simple shear flows[J]. Chemical Engineering Science，2002，57(11)：1849-1858.

［11］ Raimundo P M，Cloupet A，Cartellier A，et al. Hydrodynamics and scale-up of bubble columns in the heterogeneous regime：Comparison of bubble size，gas holdup and liquid velocity measured in 4 bubble columns from 0. 15m to 3m in diameter[J]. Chemical Engineering Science，2019，198：52-61.

［12］ 艾 涛，王少兵，王璐璐，等. 气液并流上流式反应器中的气泡特性研究[J]. 石油炼制与化工，2020，51(5)：37-41.

Ai Tao，Wang Shaobing，Wang Lulu，et al. Investigation on bubble characteristics in gas-liquid concurrent up-flow reactor[J]. Petroleum Processing and Petrochemicals，2020，51(5)：37-41(in Chinese).

［13］ 严 鹏. 鼓泡塔内气液流动行为的CFD-PBM耦合模型数值模拟[D]. 北京：北京石油化工学院，2019.

Yan Peng. Numerical Simulation of Gas-Liquid Flow Behavior in Bubble Columns Using CFD-PBM Coupled Model[D]. Beijing：Beijing Institute of Petrochemical Technology，2019(in Chinese).

［14］ Orlando A E，Barca L F，Klein T S，et al. Effects of EOR chemicals and superficial gas velocity on bubble size and gas holdup of a bubble column[J]. Oil & Gas Science and Technology-Revue d’IFP Energies nouvelles，2019，74：79.

［15］ 刘春江，卜孟庄，郭凯，等. 基于实验与CFD方法的Winpak填料混合性能研究[J]. 天津大学学报(自然科学与工程技术版)，2021，54(1)：1-9.

Liu Chunjiang，Bu Mengzhuang，Guo Kai，et al. Computational fluid dynamics simulation and experimental study of mixing performance of Winpak packing[J]. Journal of Tianjin University (Science and Technol-ogy)，2021，54(1)：1-9(in Chinese).

［16］ 王丽军，张 煜，李 希. 湍动浆态床流体力学研究(Ⅰ)气含率及其分布规律[J]. 化工学报，2008，59(12)：2996-3002.

Wang Lijun，Zhang Yü，Li Xi. Studies on hydrodynamics of slurry turbulent bubble column(Ⅰ)Gas holdup and its radial distribution[J]. CIESC Journal，2008，59(12)：2996-3002(in Chinese).

［17］ 李蔚玲. 气液固三相流态化特性的实验与数值模拟研究[D]. 南京：东南大学能源与环境学院，2016.

Li Weiling. Experiment Investigation and CFD Simulation on Fluid Dynamics of Gas-Liquid-Solid Three-Phase Bubble Column Systems[D]. Nangjing：School of Energy and Environment，Southeast University，2016(in Chinese).

［18］ Götz M，Lefebvre J，Mörs F，et al. Novel gas holdup correlation for slurry bubble column reactors operated in the homogeneous regime[J]. Chemical Engineering Journal，2017，308：1209-1224.

［19］ Islam M T，Nguyen A V. Bed expansion and gas holdup characteristics of bubble-assisted fluidization of liquid-particle suspensions in a HydroFloat cell[J]. Minerals Engineering，2021，160：106678.

［20］ 曹长青. 气-液-固三相流化床流动特性的实验研究与数值模拟[D]. 天津：天津大学化工学院，2005.

Cao Changqing. Experiment Investigation and Numerical Simulation on Hydrodynamic Characteristics in Gas-Liquid-Solid Fluidized Beds[D]. Tianjin：School of Chemical Engineering and Technology，Tianjin University，2005(in Chinese).

［21］ Wu Y，Ong B C，Al-Dahhan M H. Predictions of radial gas holdup profiles in bubble column reactors[J]. Chemical Engineering Science，2001，56(3)：1207-1210.

［22］ Eissa S H，Schügerl K. Holdup and backmixing investigations in cocurrent and countercurrent bubble columns[J]. Chemical Engineering Science，1975，30(10)：1251-1256.

［23］ Zahradnik J，Fialova M，Ru M，et al. Duality of the gas-liquid flow regimes in bubble column reactors[J]. Chemical Engineering Science，1997，52(21/22)：3811-3826.

［24］ Li H，Prakash A. Heat transfer and hydrodynamics in a three-phase slurry bubble column[J]. Industrial & Engineering Chemistry Research，1997，36(11)：4688-4694.

［25］ Sarrafi A，Muller-Steinhagen H，Smith J M，et al. Gas holdup in homogeneous and heterogeneous gas-liquid bubble column reactors[J]. The Canadian Journal of Chemical Engineering，1999，77(1)：11-21.

［26］ Luo X，Lee D J，Lau R，et al. Maximum stable bubble size and gas holdup in high-pressure slurry bubble columns[J]. AIChE Journal，1999，45(4)：665-680.

［27］ Dargar P，Macchi A. Effect of surface-active agents on the phase holdups of three-phase fluidized beds[J]. Chemical Engineering and Processing：Process Intensification，2006，45(9)：764-772.

［28］ Han L，Al-Dahhan M H. Gas-liquid mass transfer in a high pressure bubble column reactor with different sparger designs[J]. Chemical Engineering Science，2007，62(1/2)：131-139.

［29］ Yang J H，Yang J I，Kim H J，et al. Two regime transitions to pseudo-homogeneous and heterogeneous bubble flow for various liquid viscosities[J]. Chemical Engineering and Processing：Process Intensification，2010，49(10)：1044-1050.

［30］ Gandhi B，Prakash A，Bergougnou M A. Hydrodynamic behavior of slurry bubble column at high solids concentrations[J]. Powder Technology，1999，103(2)：80-94.

［31］ Zhou X H，Ma Y L，Liu M Y，et al. CFD-PBM simulations on hydrodynamics and gas-liquid mass transfer in a gas-liquid-solid circulating fluidized bed[J]. Powder Technology，2020，362：57-74.

［32］ Luo H，Svendsen H F. Theoretical model for drop and bubble breakup in turbulent dispersions[J]. AIChE Journal，1996，42(5)：1225-1233.

［33］ Safoniuk M，Grace J R，Hackman L，et al. Gas holdup in a three-phase fluidized bed[J]. AIChE Journal，2002，48(7)：1581-1587.

［34］ Law D，Jones S T，Heindel T J，et al. A combined numerical and experimental study of hydrodynamics for an air-water external loop airlift reactor[J]. Journal of Fluids Engineering，2011，133(2)：1-8.

［35］ Sari S，Ergün Ş，Barık M，et al. Modeling of isothermal bubbly flow with interfacial area transport equation and bubble number density approach[J]. Annals of Nuclear Energy，2009，36(2)：222-232.

［36］ Gidaspow D，Bezburuah R，Ding J. Hydrodynamics of circulating fluidized beds：Kinetic theory approach[R]. Chicago：Department of Chemical Engineering，1991：1-8.

［37］ Lun C K K，Savage S B，Jeffrey D J，et al. Kinetic theories for granular flow：Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield[J]. Journal of Fluid Mechanics，1984，140：223-256.

［38］ Schaeffer D G. Instability in the evolution equations describing incompressible granular flow[J]. Journal of Differential Equations，1987，66(1)：19-50.

［39］ 翟 甜. 影响鼓泡塔气-液两相流流体力学行为因素的研究[D]. 西安：西北大学化工学院，2014.

Zhai Tian. Studying the Effect Factors on Gas-Liquid Two-Phase Flow Fluid Mechanic Behaviors in Bubble Columns[D]. Xi’an：School of Chemical Engineer-ing，Northwestern University，2014(in Chinese).

［40］ Hikita H，Asai S，Tanigawa K，et al. Gas holdup in bubble columns[J]. The Chemical Engineering Journal，1980，20(1)：59-67.

［41］ Elgozali A，Linek V，Fialova M，et al. Influence of viscosity and surface tension on performance of gas-liquid contactors with ejector type gas distributor[J]. Chemical Engineering Science，2002，57(15)：2987-2994.

［42］ Begovich J M，Watson J S. Hydrodynamic characteristics of three-phase fluidized beds[R]. Oak Ridge：Oak Ridge National Lab，Tenn(USA)，1978.

［43］ 刘 刚，孙佳琦，董伟星. 改进粒子群优化算法在建筑能耗优化中的参数设置[J]. 天津大学学报(自然科学与工程技术版)，2021，54(1)：82-90.

Liu Gang，Sun Jiaqi，Dong Weixing. Selective harmonic elimination pulse width modulation based on improved hybrid particle swarm optimization[J]. Journal of Tianjin University(Science and Technology)，2021，54(1)：82-90(in Chinese).

Bubble Characteristics and Prediction Model of Gas Holdup in the Gas-Liquid-Solid Fluidized Bed

Wang Chao1, 2，Qian Dong1, 2，Zhang Lin1，Ding Hongbing1, 2

(1. School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China；2.TianjinKey Laboratory of Process Measurement and Control，Tianjin 300072，China)

The gas holdup and bubble diameter directly affect the reaction progress and mass transfer efficiency in the fluidized bed. To better understand the local flow structure，the radial gas holdup and bubble diameter distribution have become the focus of research，with the radial gas holdup prediction model demonstrating great significance. The existing average gas holdup prediction models have a limited scope of application in different experimental systems. Therefore，combined with the conductivity probe measurement and fluid simulation，a gas-liquid-solid fluidized bed with a diameter of 100mm and a height of 1.5m was considered the research object in this study. The gas holdup and bubble diameter distribution were systematically investigated under the superficial gas velocity of 0.014—0.283m/s，superficial liquid velocity of 0.007—0.028m/s，liquid viscosity of 1—40mPa·s，liquid surface tension of 0.053—0.072N/m，and solid phase volume fraction of 0—30%. Combined with the results of this experimental system and literature，a prediction model for the average gas holdup of gas-liquid-solid system was proposed. Based on this prediction model and considering the influence of superficial gas velocity and surface tension on the radial gas holdup distribution，the radial gas holdup prediction model was developed using the particle swarm optimization algorithm. The results indicate that the prediction models for the average gas holdup of two-phase and three-phase systems completely consider the effects of superficial gas velocity，superficial liquid velocity，liquid properties，solid properties，and pipe diameter. The models broaden the scope of application and improve prediction accuracy，with the mean absolute percentage error(MAPE)of 17.14% and 18.36%，respectively. Over 90% of the data points are covered by the new prediction model with a relative error of less than 30%. The radial gas holdup prediction model predicts the gas holdup near the pipeline’s center more accurately，with its MAPE reaching 12.26%. The above prediction models can prove significant in understanding the global and local mass transfer problems in the tube and the design of fluidized bed reactors.

gas-liquid-solid fluidized bed；radial gas holdup；radial bubble diameter；gas holdup prediction model

10.11784/tdxbz202204003

TE65

A

0493-2137(2023)07-0723-12

2022-04-02；

2022-07-10.

王 超（1973—  ），男，博士，教授，wangchao@tju.edu.cn.

丁红兵，hbding@tju.edu.cn.

国家自然科学基金资助项目(61627803).

Supported by the National Natural Science Foundation of China(No. 61627803).

(责任编辑：孙立华)