耦合注意力机制大坝变形改进LSTM序列到序列预测模型

王晓玲，梁羽翎，王佳俊，吴斌平，张宗亮，黄青富

耦合注意力机制大坝变形改进LSTM序列到序列预测模型

王晓玲1，梁羽翎1，王佳俊1，吴斌平1，张宗亮2，黄青富2

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 中国电建集团昆明勘测设计研究院有限公司，昆明 650051)

目前，大坝变形预测主要采用的浅层网络结构存在难以挖掘数据序列隐含深层特征的问题．常用的LSTM和GRU等模型虽然具有分析变形序列的时间自相关性特征的特点，但忽略了环境因子序列和变形序列之间的映射关系，且难以克服深度神经网络梯度下降训练易陷入局部最优的问题．针对上述问题，提出了耦合注意力机制大坝变形改进LSTM序列到序列预测模型．利用编码和解码双层LSTM构建序列到序列结构，同步提取输入影响因子和输出变形的序列特征，并耦合注意力机制，动态度量各影响因子对变形的贡献率，以提高预测精度．进一步利用蚁群信息素及双混沌优化改进鲸鱼捕食机制，构建基于改进鲸鱼优化算法的耦合注意力机制的LSTM序列到序列网络模型的无梯度环境，规避早熟收敛，弥补梯度下降本身的缺陷．工程应用结果表明，本文所提模型能够精确预测大坝变形，在各点位测试集上平均MAPE、MAE和RMSE分别为0.125%、0.604mm和0.865mm．此外，时效、水位和温度分量对点位变形的贡献率依次为51.93%、30.14%和17.93%．本研究为大坝安全监控提供理论与技术支撑．

大坝变形预测；序列到序列结构；注意力机制；改进鲸鱼优化算法；无梯度训练

坝体变形是评价大坝结构性态转异和服役健康状况的重要指标[1-2]．根据变形原型观测资料，利用统计学、机器学习等方法，建立准确的变形预测模型对大坝安全运行和风险管控意义重大[3-4]．目前常用的大坝变形预测模型存在变形监测数据深层特征分析不够深入的问题，且采用的深度神经网络存在梯度下降易陷入局部最优的问题．因此，全面挖掘数据深层特征并构建高精度变形预测模型，对大坝变形安全监测具备重要的理论和现实意义．

传统的变形预测模型主要包括确定性模型、统计模型和混合模型3类[5]，这些方法难以适应多个影响因子与变形量之间复杂的非线性关系，且易受不确定性因素干扰，模型的准确性有待提升[6]．随着人工智能技术的飞速发展，机器学习开始在大坝变形预测领域广泛使用．Zou等[7]将反向传播神经网络(back-propagation neural networks，BPNN)用于大坝变形预测研究，但BPNN通过梯度下降进行网络训练，容易陷入局部极小，且训练过程可能不稳定[8]；胡德秀等[9]将极限学习机(extreme learning machine，ELM)算法应用于大坝变形分析领域；Su等[10]提出了一种基于支持向量机(support vector machine，SVM)的大坝变形预测模型．此外，各种智能优化算法被用于基于机器学习的变形预测模型的网络训练或超参数确定，以提高预测性能．邢尹等[11]利用改进遗传算法进行BP神经网络权值和偏置的训练；Chen等[12]利用蚁狮优化算法确定最小二乘支持向量机模型中的惩罚因子及核函数超参数．

BPNN、ELM和SVM等传统浅层网络结构预测算法难以全面挖掘大坝变形监测数据序列隐含的深层特征(包括数据间映射关系、数据本身序列特征及输入数据对输出贡献率等)，而深度神经网络具备较强的挖掘能力，近年被广泛引入大坝变形预测领域．Li等[13]、冷天培等[14]利用LSTM对分解后的变形数据建立了时序预测模型．李其峰等[15]结合贝叶斯优化算法对GRU的超参数进行优化并应用于大坝变形预测．然而，目前大坝变形预测常用的深度学习序列模型如LSTM、GRU等[16]，虽然可利用其单序列训练规则进行变形时间自相关分析，但未考虑环境因子序列和变形序列之间的映射关系，亦无法在构建模型过程中同步提取输入影响因子和输出变形监测数据的序列特征，缺乏对数据深层特征的全面挖掘，影响预测精度．此外，使用梯度下降进行网络训练，难以克服易陷入局部最优、训练过程不稳定的问题．

针对上述问题，提出耦合注意力机制的改进LSTM序列到序列预测模型(improved LSTM sequence-to-sequence prediction model coupled with attention mechanism based on improved whale optimization algorithm，IWOA-ASEQ2SEQ)．为全面深入挖掘大坝变形监测数据的深层特征以提高预测精度，利用编码和解码双层LSTM构建序列到序列(sequence-to-sequence，SEQ2SEQ)结构[17]，并耦合注意力机制[18-20]，动态度量各影响因子对变形的贡献率；为弥补梯度下降易陷入局部最优的缺陷，利用蚁群信息素及双混沌优化改良鲸鱼捕食机制构建基于改进鲸鱼优化算法(improved whale optimization algorithm，IWOA)的深度网络无梯度训练环境，实现极端的探索和大规模的并行化计算[21]．

此外，本文结合糯扎渡心墙堆石坝工程进行工程应用分析．近年来，堆石坝变形预测亦常采用机器学习方法：Marandi等[22]利用遗传算法进行堆石坝坝顶沉降预测；董霄峰等[23]利用遗传算法优化BP神经网络并建立了堆石坝坝体变形预测模型；王飞等[24]建立了基于改进M5’-主成分模型树的高心墙堆石坝沉降变形预测模型；侯伟亚等[25]采用LSTM分别对变形数据时序分解后的3项进行预测并汇总各项预测结果，实现了堆石坝变形预测．本文以传统统计模型思路为基础，利用所提出的IWOA-ASEQ2SEQ模型构建影响因子与实测变形的映射关系，进行堆石坝运行期大坝变形预测分析．工程应用结果表明，本文模型能够实现准确可靠的大坝变形预测．

1 总体框架

耦合注意力机制大坝变形改进LSTM序列到序列预测模型总体框架如图1所示，包括耦合注意力机制的改进LSTM序列到序列模型和工程应用两部分.

在第1部分中，利用编码和解码双层LSTM构建序列到序列结构，并基于注意力机制形成耦合注意力机制的LSTM序列到序列模型(LSTM sequence-to-sequence model coupled with attention mechanism，ASEQ2SEQ)．该模型不仅能够全面深入挖掘大坝变形监测资料隐含的序列自相关特征，而且实现了时间特征和影响因子的信息融合，动态度量各影响因子对变形的贡献率，以深入挖掘变形效应量变化的原因；以蚁群信息素机制和双混沌优化机制改进鲸鱼优化算法(whale optimization algorithm，WOA)，提高算法的搜索速度和搜索效率；在ASEQ2SEQ模型训练阶段，利用IWOA替代梯度下降方法，构建无梯度训练环境，形成IWOA-ASEQ2SEQ以提高模型预测精度，提升训练过程的稳定性．

在第2部分中，结合糯扎渡工程实例进行了应用研究．基于工程变形观测资料，利用IWOA-ASEQ2SEQ模型构建了变形预测模型，实现了对变形观测值的精确预测并度量了各影响因子对变形的贡献率，为大坝安全监控提供理论与技术支撑．

图1 耦合注意力机制大坝变形改进LSTM序列到序列预测模型总体框架

2 耦合注意力机制的改进LSTM序列到序列模型

2.1 耦合注意力机制的LSTM序列到序列模型

提出的模型实现过程如下．

步骤1 假定原始数据集为{，}，其中影响因子矩阵由水位、时效、温度环境量及多测点变形数据构成，模型输出矩阵为变形效应量．为×矩阵，为×1矩阵；将原始数据集按模型输入要求处理为时间特征数据集{T，T}和影响因子数据集{F，F}，具体形式见式(1)～(3)．将两种数据集分离为时间特征预测层和影响因子预测层各LSTM单元的输入，即

式中：为样本数量；为输入特征维度；时间特征预测层编码及解码层时间窗口长度均为T；影响因子预测层编码及解码层时间窗口长度分别为和1；X、Y分别为矩阵和的第行第列元素．

步骤2 在编码网络的首个单元使用＜0＞、＜0＞零矩阵初始化单元状态和隐藏层状态，获取两层各单元隐藏层状态并传入各Attention单元中，以获取不同状态值的注意力权重，并将其输出作为解码网络各单元的输入，即

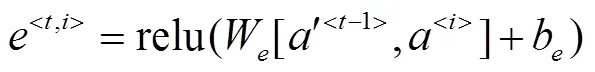
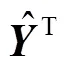
2.2 基于改进鲸鱼优化算法的无梯度训练

WOA[30]是一种新型群体智能优化算法，主要包括包围捕食阶段、螺旋更新阶段、搜寻猎物阶段3个阶段[31]，具体步骤可参考文献[30]．基本的鲸鱼优化算法存在求解精度低、收敛速度慢和易陷入局部最优的缺点，本文采用离散优化算法和连续优化算法相结合的手段[32]，利用蚁群算法信息素机制[33]提升WOA的全局寻优能力，并在局部搜索中引入双混沌优化机制[34]以处理早熟收敛问题．

具体流程如下．

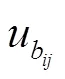
步骤2 在各子空间内生成随机数，按维度随机选取，生成种群，由个体的适应度值确定种群各个体的信息量初始值，并且得出最优个体X及其对应的信息素值为Ph．

步骤5 利用个体信息素的留存情况，计算各个体的概率权重值．再利用当前最优个体位置和概率权重值，进行种群的位置更新．

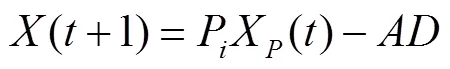
式中：＝1，2，…，；式(13)～(15)分别为信息素改进的包围捕食、螺旋更新和搜寻猎物3种位置更新方式；和为系数分量；X()为代种群最优个体；rand()为代种群随机个体．

步骤6 使用自适应权重非线性更新各个体的信息素，重复以上的步骤，直至到达预设迭代代数Max_iter，输出最优个体X(Max_iter)．

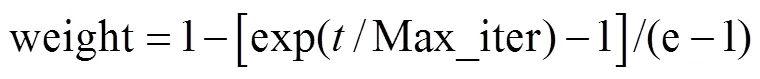
利用IWOA替代Adam梯度下降算法来进行第2.1节中ASEQ2SEQ模型的网络训练，构建无梯度训练环境，IWOA输出最优个体X(Max_iter)即为建立的变形监控模型的结构参数，即权值和偏置．形成耦合注意力机制的改进LSTM序列到序列模型对应的伪代码如下所示．

输入：原始数据集{，}，种群个体数，特征维度，最大迭代代数Max_iter，时间窗口长度T，时间特征预测层输出前向预测步T，影响因子预测层前向预测步1

处理原始数据集，获取时间特征数据集{T，T}和影响因子数据集{F，F}

利用网络参数上、下界u、l及子空间间隔dim初始化鲸鱼种群Position

while(＜Max_iter)

for Position(＝1，2，…，)

利用图１的结构获取初始各个体拟合值

利用式(10)计算各个体信息素Ph

if(Fitness＜Leader_Score)

更新当前最优目标函数值Leader_Score＝Fitness和最优个体Leader_pos＝Position

end if

end for

利用式(11)计算最优个体对应信息素Ph

利用式(13)～(15)更新种群Position

利用式(16)及(17)更新自适应权重及标定信息素

＋1

end while

return Leader_pos

输出：训练完成的大坝变形预测模型

3 工程应用

选用糯扎渡水电站大坝运行期的2015-01-11—2018-11-10期间共1400d的监测数据进行研究．选取视准线监测点中的7个点位作为本文模型的验证点位，分别为DB-L4-TP-02、DB-L5-TP-02、DB-L6-TP-02、DB-L6-TP-06、DB-L6-TP-13、DB-L7-TP-03及DB-L7-TP-13．图2为该时段典型点位观测位移、水位和日平均气温过程线．图3为心墙堆石坝下游及坝顶视准线监测点布置示意．

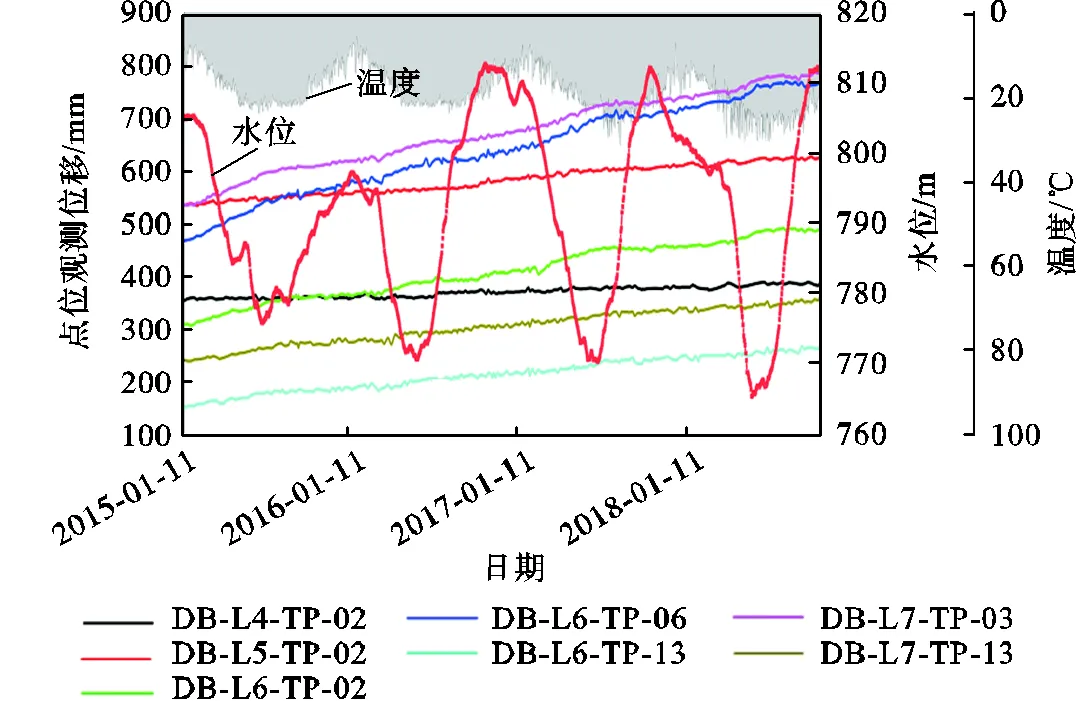
图2 典型点位观测位移、水位和日平均气温过程线

3.1 数据集准备

大坝的变形一般由水位分量、温度分量和时效分量3部分组成[35]，土石坝的变形统计模型表达式可写为

图3 下游及坝顶视准线监测点布置示意

同时，由于不同空间位置的约束条件、材料性质及荷载作用区别较大[36]，不同测点的变形无疑会存在差异．因此本文不采用统一的系统输入，而将多测点变形数据作为模型输入变形因子以构建空间维度特征，将多测点空间关联性直接集成到模型中，以考虑不同部位变形空间差异性．对于选取的7个测位的变形数据，选择其中1个作为模型输出变形效应量，而其他6个则作为模型输入的影响因子数据．故本研究最终影响因子集为

对应到式(1)～(3)的参数，输入特征维度为13；遵循选取数据70%作为训练集及30%作为验证集的原则[29]，取2015-01-11—2017-10-06期间的1000d数据作为训练集，2017-10-07—2018-11-10期间的400d数据作为测试集，故训练集和测试集分别取1000和400；T＝20，该值由改进鲸鱼优化算法迭代计算获得．

3.2 预测结果分析

运用本文模型对DB-L4-TP-02、DB-L5-TP-02、DB-L6-TP-02、DB-L6-TP-06、DB-L6-TP-13、DB-L7-TP-03和DB-L7-TP-13共7个点位进行预测分析．在100次迭代条件下，获得的预测结果如图4所示．选用平均绝对百分比误差(MAPE)、平均绝对误差(MAE)和均方根误差(RMSE)作为衡量模型性能的评价标准[35]，各点位预测性能指标结果情况如图5所示．

从图4可以看出预测值和实际值拟合程度很高，各点位预测结果与实际变形趋势基本一致．由图5可知，各点测试集平均MAPE、MAE和RMSE分别为0.125%、0.604mm和0.865mm，预测精度较高．

3.3 模型性能对比分析

为了验证本文模型相对于浅层结构算法及深度序列模型的预测性能，选择传统机器学习PSO-LSSVM算法以及深度学习的LSTM、SEQ2SEQ、ALSTM、ASEQ2SEQ模型进行对比，以DB-L6-TP-13为例，100次迭代获取的预测结果如图6所示．图7为6种模型的预测性能指标对比情况．

由图6可知：IWOA-ASEQ2SEQ模型预测值与实测值的偏离程度最低，相同迭代次数下，SEQ2SEQ和ALSTM较LSTM拟合效果更好，ASEQ2SEQ算法与SEQ2SEQ相比更贴近实测点．IWOA-ASEQ2SEQ模型拟合情况最优，证明本文模型能有效预测变形的动态变化过程．

从图７可以看出：①相同迭代次数下，5种深度学习序列模型3种指标均优于PSO-LSSVM算法，说明挖掘数据深层特征可提升模型精度；②SEQ2SEQ较LSTM模型平均性能提升达3.06%，ALSTM较LSTM模型的平均性能提升达27.67%，ASEQ2SEQ较SEQ2SEQ模型性能上平均增幅38.08%，说明同步提取输入影响因子和输出变形的序列特征和耦合注意力机制在提升整体预测精度方面的作用；③IWOA-ASEQ2SEQ对应的MAPE、MAE和RMSE均小于其他５种模型，预测精度最高，相较于ASEQ2SEQ模型平均性能提升达37.12%，说明利用改进鲸鱼优化算法进行网络权重偏置的迭代计算对模型性能有显著提升作用．

3.4 因子贡献率分析

大坝变形领域引入深度学习方法，是借其对监测数据深层特征的强挖掘能力，实现高精度的变形预测．但是目前常用的LSTM及GRU等深度神经网络，均为“黑盒模型”，其可解释性的缺失降低了模型的可信度．本文的耦合注意力机制的改进LSTM序列到序列预测模型不仅大幅提高预测准确性，而且利用注意力机制原理动态地度量各因子对输出变形的贡献率，增加模型的可信度．

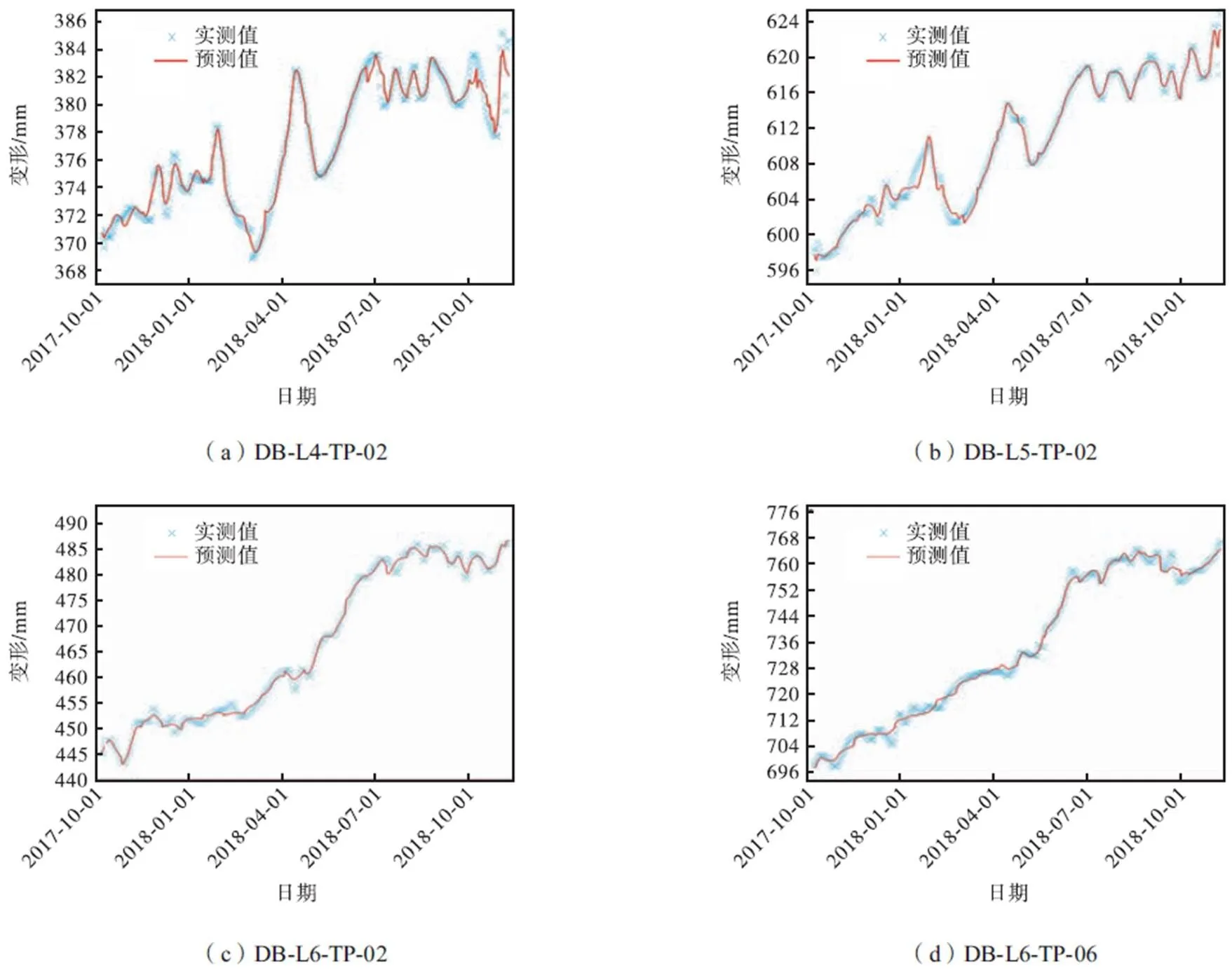
图5 各点预测性能指标结果

图8展示点位DB-L6-TP-13测试集上的7个环境因子和6个其他测点变形因子时序注意力权重．图9为环境因子和变形因子的平均注意力权重．

图6 6种模型的预测结果对比

图7 6种模型的预测性能指标对比

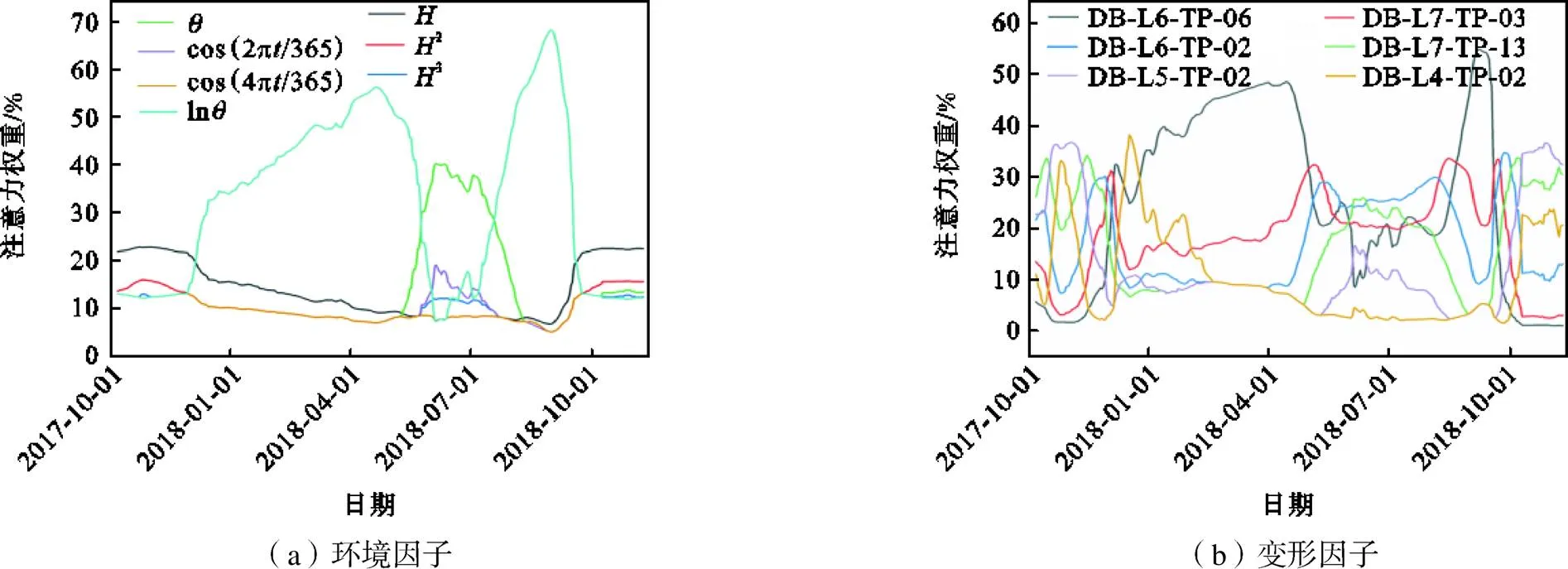
图8 各因子时序注意力权重

图9 各因子平均注意力权重

根据土石坝变形长期研究，在统计模型中，时效分量影响最大，水位分量影响较小，温度分量的影响可忽略不计[32]．这与本文计算获得的各分量的注意力权重结果一致．此外，由图3可知，从与DB-L6-TP-13的点位布设距离来看，DB-L6-TP-06最近，同一视准线上点位DB-L6-TP-02和同一桩号上点位DB-L7-TP-13距离较近，DB-L7-TP-03距离稍远，而DB-L5-TP-02和DB-L4-TP-02距离最远．而点位与点位之间距离越近，相互间变形影响越大，这与图8及图9的因子贡献率分析结果基本吻合．

4 结 论

本文构建了耦合注意力机制大坝变形改进LSTM序列到序列预测模型，利用序列到序列结构并耦合注意力机制全面挖掘大坝变形监测数据的深层特征，并基于改进鲸鱼优化算法构建ASEQ2SEQ网络模型的无梯度训练环境，解决梯度下降易陷入局部最优等问题．工程应用分析表明，本文模型预测精度极高，且能够获取各影响因子贡献率，可为大坝安全诊断提供可靠分析结果，主要结论如下．

(1)提出了耦合注意力机制的LSTM序列到序列模型．利用编码和解码双层LSTM构建序列到序列结构并耦合注意力机制，在建模过程中提取变形观测数据的深层特征，提升了变形预测模型的拟合效果，极大提高了模型预测精度．

(2)在ASEQ2SEQ模型训练阶段，基于改进鲸鱼优化算法替代梯度下降进行网络训练，通过构建无梯度训练环境弥补了深度学习框架误差反向传播时易陷入局部最优的不足，规避了早熟收敛，提高了训练过程的稳定性和模型的精度．

(3)选用糯扎渡工程坝体变形观测资料进行研究，本文模型在各点位测试集上平均MAPE、MAE和RMSE分别为0.125%、0.604mm和0.865mm，相比于PSO-LSSVM、LSTM、SEQ2SEQ、ALSTM、ASEQ2SEQ模型具有更高预测精度；预测结果显示环境因子中，时效分量贡献率最大，其次是水位分量，温度分量最小，这与长期工程研究结果一致；变形因子的贡献率结果亦符合点位之间距离越近、相互间变形影响越大的基本规律．

综上，本文提出的IWOA-ASEQ2SEQ模型能够准确、可靠地预测大坝变形，为大坝安全监控提供理论与技术支撑．

［1］ 谷艳昌，王士军，庞 琼，等. 基于风险管理的混凝土坝变形预警指标拟定研究[J]. 水利学报，2017，48(4)：480-487.

Gu Yanchang，Wang Shijun，Pang Qiong，et al. Study on early warning index of concrete dam’s deformation based on the risk management[J]. Shuili Xuebao，2017，48(4)：480-487(in Chinese).

［2］ 李明军，王均星，王亚洲. 基于改进粒子群优化算法和极限学习机的混凝土坝变形预测[J]. 天津大学学报(自然科学与工程技术版)，2019，52(11)：1136-1144.

Li Mingjun，Wang Junxing，Wang Yazhou. Deformation prediction of concrete dam based on improved particle swarm optimization algorithm and extreme learning machine[J]. Journal of Tianjin University(Science and Technology)，2019，52(11)：1136-1144(in Chinese).

［3］ 周仁练，苏怀智，韩 彰，等. 混凝土坝变形的长期预测模型与应用[J]. 水力发电学报，2021，40(9)：122-131.

Zhou Renlian，Su Huaizhi，Han Zhang，et al. Long-term deformation prediction model of concrete dams and its application[J]. Journal of Hydroelectric Engineering，2021，40(9)：122-131(in Chinese).

［4］ 刘大文，胡建忠. 工程安全监测技术[M]. 北京：中国水利水电出版社，2007.

Liu Dawen，Hu Jianzhong. Engineering Safety Monitoring Technology[M]. Beijing：China Water and Power Press，2007(in Chinese).

［5］ Kang F，Liu J，Li J，et al. Concrete dam deformation prediction model for health monitoring based on extreme learning machine[J]. Structural Control Health Monitoring，2017，24(10)：e1997.

［6］ Shao C，Gu C，Yang M，et al. A novel model of dam displacement based on panel data[J]. Structural Control Health Monitoring，2018，25(1)：e2037.

［7］ Zou J，Bui K-T T，Xiao Y，et al. Dam deformation analysis based on BPNN merging models[J]. Geo-Spatial Information Science，2018，21(2)：149-157.

［8］ 廖坤锐，陈卫兵，杨 雪. 基于 PCA 和粒子群优化算法的焊点缺陷识别[J]. 计算机测量与控制，2020，28(5)：190-194.

Liao Kunrui，Chen Weibing，Yang Xue. Solder joint defect recognition based on PCA and particle swarm optimization algorithm[J]. Computer Measurement and Control，2020，28(5)：190-194(in Chinese).

［9］ 胡德秀，屈旭东，杨 杰，等. 基于 M-ELM 的大坝变形安全监控模型[J]. 水利水电科技进展，2019，39(3)：75-80.

Hu Dexiu，Qu Xudong，Yang Jie，et al. A safety monitoring model of dam deformation based on M-ELM[J]. Advances in Science and Technology of Water Resources，2019，39(3)：75-80(in Chinese).

［10］ Su H，Li X，Yang B，et al. Wavelet support vector machine-based prediction model of dam deformation[J]. Mechanical Systems and Signal Processing，2018，110：412-427.

［11］ 邢 尹，陈 闯，刘立龙，等. 改进遗传算法和 BP 神经网络的大坝变形预测[J]. 计算机工程与设计，2018，39(8)：2628-2631，2686.

Xing Yin，Chen Chuang，Liu Lilong，et al. Dam deformation prediction based on improved genetic algorithm and BP neural network[J]. Computer Engineering and Design，2018，39(8)：2628-2631，2686(in Chinese).

［12］ Chen Y，Gu C，Shao C，et al. An approach using adaptive weighted least squares support vector machines coupled with modified ant lion optimizer for dam deformation prediction[J]. Mathematical Problems in Engineering，2020，2020：9434065.

［13］ Li Y，Bao T，Gong J，et al. The prediction of dam displacement time series using STL，extra-trees，and stacked LSTM neural network[J]. IEEE Access，2020，8：94440-94452.

［14］ 冷天培，马 刚，向正林，等. 基于时序分解与深度学习的堆石坝变形预测[J]. 水力发电学报，2021，40(10)：147-159.

Leng Tianpei，Ma Gang，Xiang Zhenglin，et al. Deformation prediction of rockfill dams based on time series decomposition and deep learning[J]. Journal of Hydroelectric Engineering，2021，40(10)：147-159(in Chinese).

［15］ 李其峰，杨 杰，程 琳，等. 基于BO-GRU的混凝土坝变形预测模型[J]. 水资源与水工程学报，2021，32(4)：180-184，193.

Li Qifeng，Yang Jie，Cheng Lin，et al. Deformation prediction model of concrete dams based on BO-GRU model[J]. Journal of Water Resources and Water Engineering，2021，32(4)：180-184，193(in Chinese).

［16］ 杨 丽，吴雨茜，王俊丽，等. 循环神经网络研究综述[J]. 计算机应用，2018，38(增2)：1-6，26.

Yang Li，Wu Yuxi，Wang Junli，et al. Research on recurrent neural network[J]. Journal of Computer Applications，2018，38(Suppl 2)：1-6，26(in Chinese).

［17］ 赵阳洋，王振宇，王 佩，等. 任务型对话系统研究综述[J]. 计算机学报，2020，43(10)：1862-1896.

Zhao Yangyang，Wang Zhenyu，Wang Pei，et al. A survey on task-oriented dialogue systems[J]. Chinese Journal of Computers，2020，43(10)：1862-1896(in Chinese).

［18］ 郑育靖，何 强，张长伦，等. 基于 GRU-Attention 的无监督多变量时间序列异常检测[J]. 山西大学学报(自然科学版)，2020，43(4)：756-764.

Zheng Yujing，He Qiang，Zhang Changlun，et al. GRU-Attention based unsupervised multivariate time series anomaly detection[J]. Journal of Shanxi University(Natural Science Edition)，2020，43(4)：756-764(in Chinese).

［19］ Su Y，Weng K，Lin C，et al. Dam deformation interpretation and prediction based on a long short-term memory model coupled with an attention mechanism[J]. Applied Sciences，2021，11(14)：6625.

［20］ 王晓玲，李 克，张宗亮，等. 耦合 ALO-LSTM 和特征注意力机制的土石坝渗压预测模型[J]. 水利学报，2022，53(4)：403-412.

Wang Xiaoling，Li Ke，Zhang Zongliang，et al. Coupled ALO-LSTM and feature attention mechanism prediction model for seepage pressure of earth-rock dam[J]. Shuili Xuebao，2022，53(4)：403-412(in Chinese).

［21］ Stanley K O，Clune J，Lehman J，et al. Designing neural networks through neuroevolution[J]. Nature Machine Intelligence，2019，1(1)：24-35.

［22］ Marandi S M，VaeziNejad S M，Khavari E. Prediction of concrete faced rock fill dams settlements using genetic programming algorithm[J]. International Journal of Geosciences，2012，3(3)：601-609.

［23］ 董霄峰，王海军，杨 敏. 基于遗传算法优化 BP 神经网络的面板堆石坝变形预测[J]. 水利水电技术，2012，43(12)：22-25.

Dong Xiaofeng，Wang Haijun，Yang Min. Prediction on deformation of concrete face rockfill dam based on BP neural network optimized by genetic algorithm[J]. Water Resources and Hydropower Engineering，2012，43(12)：22-25(in Chinese).

［24］ 王 飞，张宗亮，王佳俊，等. 基于改进M5’-主成分模型树的高心墙堆石坝沉降变形预测[J]. 河海大学学报(自然科学版)，2018，46(4)：353-359.

Wang Fei，Zhang Zongliang，Wang Jiajun，et al. Forecasting of the settlement deformation for high core rock-fill dam based on the improved M5’-PCR model tree[J]. Journal of Hohai University(Natural Sciences)，2018，46(4)：353-359(in Chinese).

［25］ 侯伟亚，温彦锋，邓 刚，等. 联合时序分解和深度学习的高土石坝变形预测[J]. 水力发电学报，2022，41(3)：123-132.

Hou Weiya，Wen Yanfeng，Deng Gang，et al. Deformation prediction of high embankment dams by combining time series decomposition and deep learning[J]. Journal of Hydroelectric Engineering，2022，41(3)：123-132(in Chinese).

［26］ Yang B，Sun S，Li J，et al. Traffic flow prediction using LSTM with feature enhancement[J]. Neurocomputing，2019，332：320-327.

［27］ Chen Y，Peng G，Zhu Z，et al. A novel deep learning method based on attention mechanism for bearing remaining useful life prediction[J]. Applied Soft Computing，2020，86：105919.

［28］ Wang J，Yan J，Li C，et al. Deep heterogeneous GRU model for predictive analytics in smart manufacturing：Application to tool wear prediction[J]. Computers in Industry，2019，111：1-14.

［29］ Liu W，Pan J，Ren Y，et al. Coupling prediction model for long-term displacements of arch dams based on long short-term memory network[J]. Structural Control Health Monitoring，2020，27(7)：e2548.

［30］ Mirjalili S，Lewis A. The whale optimization algorithm[J]. Advances in Engineering Software，2016，95：51-67.

［31］ 武泽权，牟永敏. 一种改进的鲸鱼优化算法[J]. 计算机应用研究，2020，37(12)：3618-3621.

Wu Zequan，Mu Yongmin. Improved whale optimization algorithm[J]. Application Research of Computers，2020，37(12)：3618-3621(in Chinese).

［32］ 马玉泉. 基于遗传算法的离散多目标优化问题研究及其应用[D]. 兰州：兰州理工大学电气工程与信息工程学院，2019.

Ma Yuquan. Research and Application of Discrete Multi-objective Optimization Based on Genetic Algorithms[D]. Lanzhou：College of Electrical and Information Engineering，Lanzhou University of Technology，2019(in Chinese).

［33］ 李世威，王建强，曾俊伟. 遗传算法调整蚁群算法参数模型研究[J]. 计算机工程与设计，2011，32(10)：3490-3493，3502.

Li Shiwei，Wang Jianqiang，Zeng Junwei. Model of ant colony algorithm parameters optimization based on genetic algorithm[J]. Computer Engineering and Design，2011，32(10)：3490-3493，3502(in Chinese).

［34］ 姜建国，刘梦楠，刘永青，等. 一种采用双混沌搜索的类电磁机制算法[J]. 西安电子科技大学学报(自然科学版)，2014，41(5)：79-83，147.

Jiang Jianguo，Liu Mengnan，Liu Yongqing，et al. Electromagnetism-like mechanism algorithm via dual chaotic search[J]. Journal of Xidian University，2014，41(5)：79-83，147(in Chinese).

［35］ 王晓玲，谢怀宇，王佳俊，等. 基于 Bootstrap 和 ICS-MKELM 算法的大坝变形预测[J]. 水力发电学报，2020，39(3)：106-120.

Wang Xiaoling，Xie Huaiyu，Wang Jiajun，et al. Prediction of dam deformation based on Bootstrap and ICS-MKELM algorithms[J]. Journal of Hydroelectric Engineering，2020，39(3)：106-120(in Chinese).

［36］ 吴中如，陈 波. 大坝变形监控模型发展回眸[J]. 现代测绘，2016，39(5)：1-3，8.

Wu Zhongru，Chen Bo. A review on development of dam safety monitoring models[J]. Modern Surveying and Mapping，2016，39(5)：1-3，8(in Chinese).

Improved LSTM Sequence-to-Sequence Prediction Model for Dam Deformation Coupled with Attention Mechanism

Wang Xiaoling1，Liang Yuling1，Wang Jiajun1，Wu Binping1，Zhang Zongliang2，Huang Qingfu2

(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2. PowerChina Kunming Engineering Corporation Limited，Kunming 650051，China)

At present, the shallow network structure which is mainly used for dam deformation prediction is difficult to mine the hidden deep characteristics of data series. Moreover, although the commonly used models such as LSTM and GRU can analyze the temporal autocorrelation characteristics of deformation series, they ignore the mapping relationship between the environmental factor series and deformation series, and it is difficult to overcome the problem that the gradient descent training of deep neural network is easy to fall into local optimums. To solve these problems, an improved LSTM sequence-to-sequence prediction model for dam deformation coupled with attention mechanism was proposed. The sequence-to-sequence structure was constructed by encoding and decoding a double-layer LSTM, and the sequence characteristics of influencing factors for input and output deformation were extracted synchronously. The contribution rate of each influencing factor with respect to deformation was measured dynamically by coupling the attention mechanism to improve prediction accuracy. Furthermore, ant colony pheromones and double-chaos optimization were used to improve the whale feeding mechanism, so as to construct a gradient-free environment from the LSTM sequence-to-sequence network model coupled with attention mechanism based on the improved whale optimization algorithm. In this way, the premature convergence is avoided and the defect of gradient descent itself is corrected. The results of engineering applications show that the proposed model can accurately predict dam deformation. The average MAPE on a test set of different points is 0.125%, and the corresponding average values of MAE and RMSE are 0.604 mm and 0.865 mm, respectively. In addition, the contribution rates of aging, water level and temperature with respect to point deformation are 51.93%, 30.14% and 17.93%, respectively. This study provides a theoretical and technical support for dam safety monitoring.

dam deformation prediction；sequence-to-sequence structure；attention mechanism；improved whale optimization algorithm(IWOA)；gradient-free training

10.11784/tdxbz202203057

TV698.11

A

0493-2137(2023)07-0702-11

2022-03-29；

2022-05-19.

王晓玲（1968—  ），女，博士，教授，wangxl@tju.edu.cn.

王佳俊，jiajun_2014_bs@tju.edu.cn.

国家自然科学基金雅砻江联合基金资助项目(U1965207，U1865204).

Supported by the Yalong River Joint Funds of the National Natural Science Foundation of China(No.U1965207，No. U1865204).

(责任编辑：武立有)