基于加权运动平均的多视角点云鲁棒配准方法

刘海涛，黄玉庚，肖聚亮，岳 巍

基于加权运动平均的多视角点云鲁棒配准方法

刘海涛，黄玉庚，肖聚亮，岳 巍

(天津大学机构理论与装备设计教育部重点实验室，天津 300354)

本文提出一种基于加权运动平均的多视角点云配准方法，有效提高了多视角点云配准的效率和精度. 首先，通过双视角点云配准算法得到点集的相对运动集；提出一种分层渐进式点云配准初值确定方法，该方法计算运动关系图中三视匹配元一致性度量，逐步挑选最为可靠的匹配元进行顶点初值化与顶点扩展，有效避免了因所选初值与真值偏差较大导致加权运动平均效果不佳的问题；依据上述方法确定配准初值，并根据该初值判断双视角匹配结果的可靠性，以剔除相对运动集内包含的外点，最后将剔除外点后的原始相对运动集的内点子集作为加权运动平均算法输入的相对运动集. 以斯坦福公开数据集为对象开展了对比实验，基于双视角配准算法分别获得了4个测试点集在30%、25%和20%双视角点云重叠率阈值下的双视角配准结果，共形成12组相对运动集. 其中，相对运动集误差随重叠率阈值的下降逐渐增加. 所提方法在12组运动集上均获得了最佳的配准结果，证明了本文所提出方法在提高加权运动平均方法计算精度与效率方面的有效性. 此外，当运动集包含大量外点时，采用本文所提方法仍能获得较为准确的配准结果，证明了本文所提方法的强鲁棒性.

多视角点云配准；加权运动平均；回环一致性；分层渐进

点云配准在工业测量、计算机视觉和机器人移动建图等领域应用广泛[1-2]．根据待配准点集中点云的帧数，点云配准问题可分为两类：双视角点云配准与多视角点云配准问题．

双视角点云配准是实现多视角点云配准的基础.近几十年内，相关学者对该问题进行了广泛研究，并提出一系列配准方法．其中，文献[3]提出的迭代最近点(iterative closest point，ICP)算法及其衍生算法最为常用．该方法基于迭代求解思想，可实现刚体的有效配准．然而，当双帧点云仅部分区域重叠时，ICP算法失效．为了解决上述问题，文献[4]提出了裁剪ICP(trimmed iterative closest point，TrICP)算法，其在ICP算法的基础上引入重叠百分比参数，通过去除非重叠区域，得到双视角点云的准确配准结果．

多视角点云配准的目标是计算点集中各帧点云和基准点云之间的刚体变换矩阵，继而将物体或环境中多个视角扫描测量得到的点云映射到全局坐标系中[2]．为了解决多视角配准问题，Govindu等[5]首次提出了基于运动平均算法的多视角点云配准方法，该方法将所有可获得的双视角点云配准结果作为输入，并借助李代数平均算法计算各变换矩阵．值得指出的是，运动平均算法虽然可作为解决多视角点云配准问题的有效手段，但没有考虑每个双视角匹配结果的可靠性和准确性．为了避免上述问题，Guo等[6]通过TrICP算法计算双视角点云的重叠百分比，并将其视为每个匹配对的权重，提出了加权运动平均方法．该方法可在一定程度上提高运动平均算法的有效性和鲁棒性．然而，考虑到TrICP算法易陷入局部最优，因此，借助该算法衡量的重叠百分比的准确性无法保证[7]．此外，Li等[7]基于低秩稀疏矩阵分解算法提出了一种自适应加权运动平均方法，利用拉格朗日乘子计算每个相对运动的权重．

虽然基于运动平均算法的配准方法能够有效解决多视角点云配准问题，但需要指出的是，运动平均算法实质为高斯牛顿迭代法，即通过多次迭代计算问题的加权最小二乘解．当给定初值偏离全局最优解时，算法容易陷入局部最优，因此，上述算法依赖于良好的配准初值．运动平均算法中用于计算配准初值的方法主要包括广度搜索生成树方法和低秩稀疏矩阵分解(low-rank and sparse decomposition，LRS)方法[8]．其中，广度搜索生成树方法将其中某一帧点云视为基础帧，以此作为基点进行广度搜索．该方法原理简单，然而当相对运动集中包含大量外点时，无法确保遍历的双视角匹配结果的可靠性；LRS算法虽然能够在相对运动集中包含外点的情况下得到较好的配准初值，但其精度容易受到图的稀疏性影响．综上所述，尽管现有方法能够求解点云配准初值，但相关算法的精度还有待进一步提高．

1 加权运动平均及其初值问题

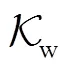
图1 点集的相对运动与全局运动关系

Fig.1　　Representation of relative and global motions of data set

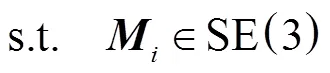
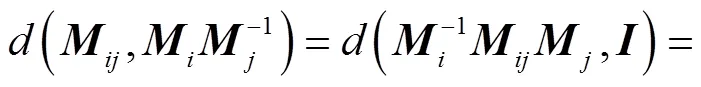
若忽略式(9)和式(10)中的一阶小量，进一步可得

将式(11)代入式(8)中，有

将式(14)改写为矩阵形式，即

2 鲁棒多视角点云配准方法

2.1 三视匹配元一致性度量

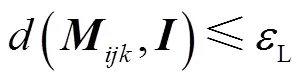
2.2 基于三视匹配元一致性度量的初值确定方法

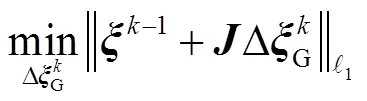
2.2.2 初值确定方法流程

鉴于加权运动平均算法的有效性依赖于良好的迭代初值，而合理的初值确定方式是有效避开运动关系视图中的外点，故本节提出了基于三视匹配元一致性度量的多视角点云配准初值确定方法，其核心思想是：在初始化阶段，逐步添加最可靠的三视匹配元，以运动关系视图中连通分量度数最大的顶点对应的点云作为基础帧点云；在扩展阶段，基于已确定初值的顶点不断扩展，直至确定所有顶点的初值．算法可分为如下3个步骤．

步骤1 顶点初始化．

图2 本文方法步骤1示意

步骤2 顶点扩展．

图3 本文方法步骤2的示意

给定无序多视角点集，利用上述方法可获得较为精准的配准初值．算法1给出了本文所提方法的整体流程．与基于生成树的方法不同，本文所提方法在顶点的扩展过程中引入了三视匹配元一致性度量，以度数最大的顶点作为基顶点，而非默认将点集的第1帧或任意帧作为基础帧，且采用分层增量的方法进行顶点的扩展，降低了外点的影响并有效减小了累积误差．算法1伪代码如下．

算法1 渐进式点云配准初值确定方法

repeat

repeat

end for

end while

2.3 外点剔除

由第1节可知，相对运动集易受到外点的污染，因此根据第2.2节所提方法确定配准初值后，为了获得更为精确的内点集合，本节进一步设计用于筛选内点的准则．

综上，结合第2.2节提出的初值确定方法，算法2示出了本文所提鲁棒运动平均方法的整体流程．此外，本文权重因子可根据文献[9]提出的方法确定，限于篇幅，不再赘述．算法2的伪代码如下．

算法2 基于加权运动平均的多视角点云鲁棒配准方法

end for

end for．

repeat

end for

3 实验与结果分析

本文利用斯坦福公开数据集[14]测试所提出方法的精度和效率，以验证其有效性与鲁棒性．在斯坦福数据集中共选取了Armadillo、Buddha、Bunny、Dragon 4个点集作为实验对象，其点云帧数分别为12、15、10、15，图4示出了未进行配准前4个数据集的三维点云．

图4 4个数据集未进行配准前的三维模型

为体现本文所提方法的优势，将其与文献[9]、文献[5]提出的运动平均方法和文献[8]提出的低秩稀疏矩阵分解方法(分别简记为WMA、MA、LRS)进行比较．此外，为揭示配准初值对运动平均方法的影响，本文以LRS方法和本文所提出的渐进式配准初值确定方法(简记为OurInit)得到的结果分别作为MA、WMA算法的输入进行对比实验．其中，LRS方法的源代码作者已提供，其采用MATLAB编程实现，其余方法均采用C++编程实现，所有实验程序均在RAM为16GB、主频为2.90GHz的16核笔记本电脑上运行．

3.1 精度与效率对比实验

为比较不同配准方法的性能，进行了对比实验．首先选取4个点集中30%重叠率阈值下的双帧点云，并进行配准，以获得作为配准算法输入的相对运动集结果．表1给出了各个测试点集对应相对运动集的匹配对数量、旋转误差和平移误差．表2给出了采用不同配准方法配准4个测试点集时的旋转、平移误差以及耗时的比较结果．为进一步对比不同方法的精度，图5采用横截面的形式示出了各种方法的配准结果，其中，MA-LRS、MA-OurInit分别表示采用MA算法以LRS和本文所提初值确定方法作为初值时的配准结果，同理，WMA-LRS、WMA-OurInit表示采用WMA算法以LRS和本文所提初值确定方法作为初值时的配准结果．图6为采用本文所提初值确定方法对Dragon数据集进行初值确定的过程示意.

表1在30%重叠率阈值下的匹配对配准结果组成的相对运动集的误差统计结果和匹配对数量

Tab.1　　Error statistics information and the number of relative motions consisted of the pair-wise regis-trations of scan pairs with 30% overlap percentage threshold

表2 不同配准方法在测试点集上的配准误差与运行时间对比结果

Tab.2 Registration errors and runtimes of different multi-view registration methods on four data sets

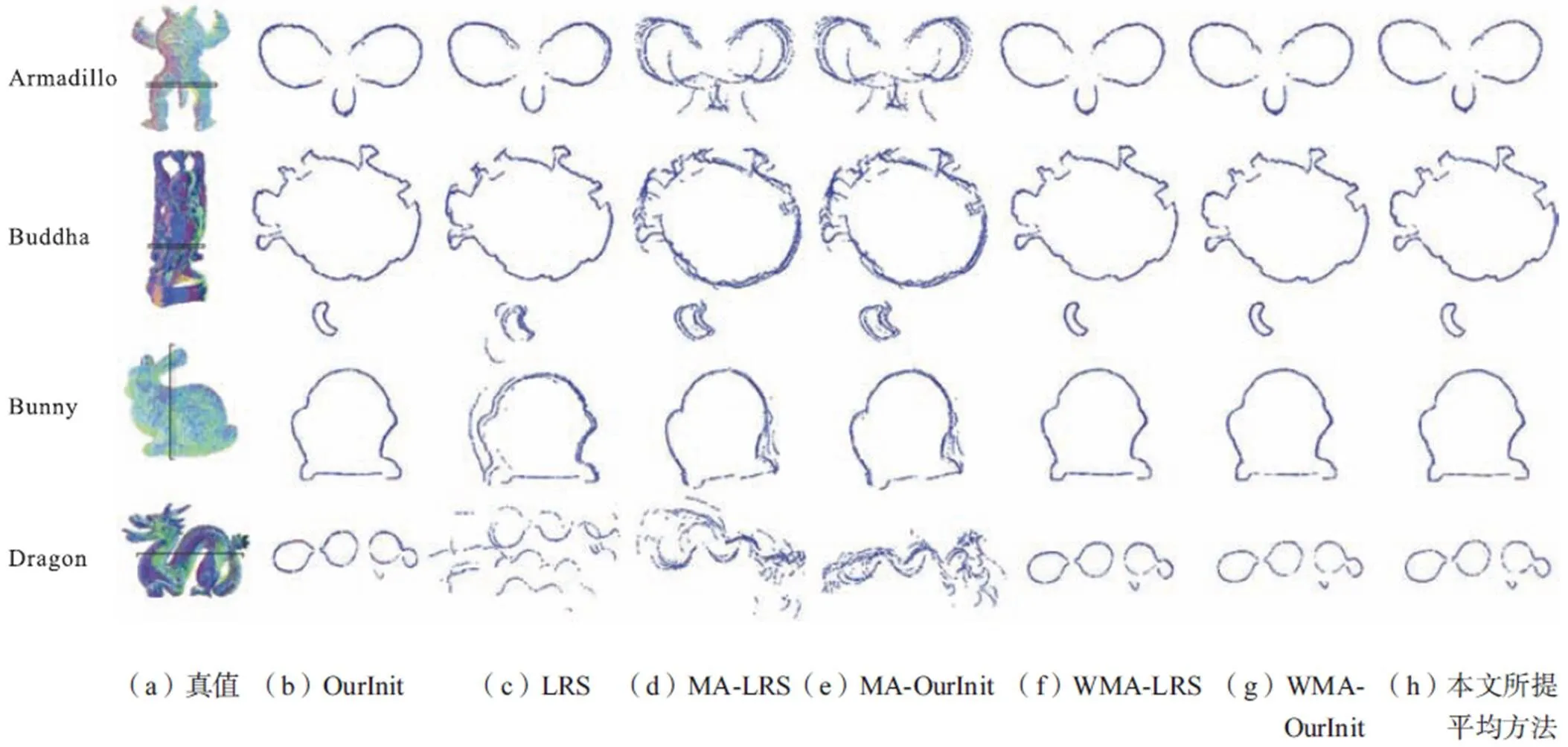
图5 以横截面形式呈现的不同配准方法在4个测试点集上的配准结果对比

图6 在30%重叠率阈值下本文所提初值确定方法对Dragon数据集进行初值确定的过程示意

由表2可知，相较于LRS方法，采用本文方法确定的初值旋转误差与平均误差均为最小，说明所提初值确定算法具有较好的精度．LRS方法精度不高的解释如下：LRS方法采用低秩稀疏矩阵分解进行全局运动求解，但由于点云配准问题中部分点云的重叠百分比较低，导致图较为稀疏，从而导致LRS方法精度受限[8]．本文方法则依赖于三视匹配元一致性度量进行顶点的扩展，因此，图中存在一致性较好的匹配元是保证本文算法精度的前提．值得指出的是，在实际应用中，因为表面遮挡与扫描面积的局限，为了获得物体的表面完整的三维点云需要对被测物体进行多个视角的扫描，这便有效地满足了上述前提．

结合表1和表2可见，MA算法的精度最差，因为该算法把不可靠和可靠的匹配对配准结果均赋予相同的权重，因此，在相对运动集包含较多外点的情况下，MA算法无法保证算法的精度．较于WMA方法，本文所提方法的配准精度更高．因为尽管本文所提方法的核心与WMA和MA两种方法一致，均采用高斯牛顿迭代法求解，但本文方法精确地确定了配准初值，并剔除了外点，因此实际上该算法的输入并非包含大量外点的相对运动集，而是其内点子集，从而提高了多视角点云配准结果的精度．值得指出的是，本文基于三视匹配元一致性不断进行顶点的扩展，即所有扩展的边与顶点组成的图是连通的，因此作为算法输入的内点集合中各帧点云之间均存在有效关联．

3.2 配准算法的鲁棒性实验与初值影响对比实验

为说明本文所提方法的鲁棒性并揭示不同初值对配准算法的影响，本文在不同重叠率阈值下进行了对比实验．首先对4个点集中重叠率分别大于25%、20%的双帧点云进行配准，以此获得对比实验的相对运动集．表3和表4分别给出了不同重叠率阈值下各个测试点集对应的相对运动集的匹配对数量、旋转误差和平移误差．结合表1可见，随着重叠率的下降，测试点集对应的相对运动集中的误差逐增，说明运动集中受外点污染的程度也随着重叠率的下降不断增加．表5和表6分别示出了采用不同配准方法以上述相对运动集作为输入配准点集时的旋转、平移误差以及耗时的比较结果．

表3在25%重叠率阈值下的匹配对配准结果组成的相对运动集的误差统计结果和匹配对数量

Tab.3　　Error statistics information and the number of relative motions consisted of the pair-wise regis-trations of scan pairs with 25% overlap percentage threshold

表4在20%重叠率阈值下的匹配对配准结果组成的相对运动集的误差统计结果和匹配对数量

Tab.4　　Error statistics information and the number of rela-tive motions consisted of the pair-wise registrations of scan pairs with 20% overlap percentage threshold

为说明初值对运动平均方法的影响和本文方法的高效性与鲁棒性，图7示出了不同重叠率下WMA-LRS、WMA-OurInit、OurInit和本文所提配准方法对Buddha(25%重叠率阈值)和Dragon(20%重叠率阈值)点集进行配准后的距离误差映射图．

结合表2、表5和表6示出的各种配准算法在不同重叠率下的实验结果对比可知，随着相对运动集中受外点污染程度的增加，LRS和MA方法获得的配准结果越发偏离真实值，其原因在于，MA方法对不可靠的匹配结果极其敏感，即使相对运动集中存在一个外点也可能导致MA方法配准失败[17]．相比于MA方法，LRS方法对不可靠的匹配结果较为鲁棒[17]，但在Buddha、Dragon测试点集上的配准结果表明，随着不可靠匹配结果的增加，LRS方法的精度将不断下降，甚至导致配准失败．

表5 不同配准方法在25%重叠率阈值下对测试点集进行配准后的配准误差与运行时间对比结果

Tab.5 Registration errors and runtimes of different multi-view registration methods on four data sets with 25% overlap percentage threshold

表6 不同配准方法在20%重叠率阈值下对测试点集进行配准后的配准误差与运行时间对比结果

Tab.6 Registration errors and runtimes of different multi-view registration methods on four data sets with 20% overlap percentage threshold

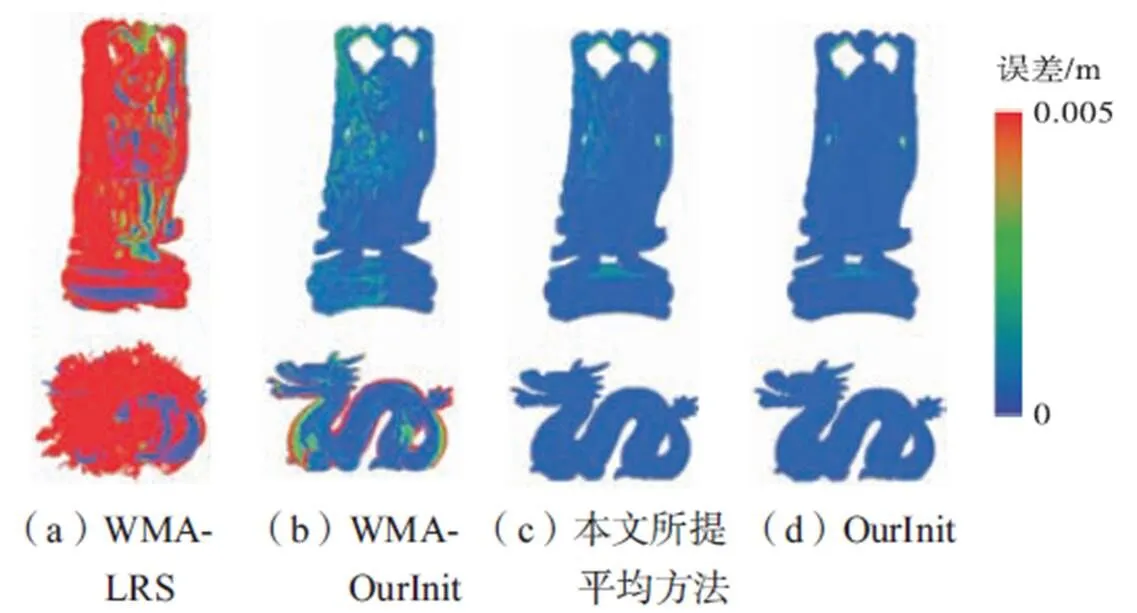
图7　　不同方法在Buddha测试集(25%重叠率阈值)和Dragon测试集(20%重叠率阈值)上的距离误差映射图

结合表2、表5、表6与图7可知，尽管相对运动集中包含大量外点，对于4个测试点集，本文所提初值确定方法和最终配准方法均能获得最佳和次之的配准结果．因此，在不同重叠率阈值下的对比实验结果证明了本文方法的鲁棒性和有效性．值得指出的是，随着相对运动集中匹配对数量的不断增加，本文所提初值确定方法程序运行时间并无明显的增加．表5和表6中的Dragon实验结果表明，随着匹配对数量的增加，本文所提初值确定方法求解程序的运行时间有所减少，且所确定的初值相比于最终运动平均方法获得的配准结果精度更高．为了揭示该现象产生的原因，图8所示为在20%重叠率阈值下采用本文所提初值确定方法对Dragon数据集进行初值确定的过程示意．对比图6示出的30%重叠率阈值下的顶点扩展的顺序图可知，尽管在20%阈值下，(0，3)、(0，12)、(2，12)等匹配对的重叠率较低，其仍能获得较佳的配准结果．于是在匹配对(0，3)与(2，3)的关联下，顶点3在第2轮顶点扩展时便已确定初值，无需进行第3轮扩展，且在(0，12)、(2，12)等匹配对的作用下，连通块的联结性更强，从而导致20%重叠率阈值下所提出方法实验结果的精度高于30%重叠率阈值下的实验结果．综上，本文提出的初值确定方法能基于三视匹配元一致性度量隐性地剔除相对运动集中不可靠的匹配结果，因此，尽管随着重叠率的下降，本文所提初值确定方法依旧能在一定程度上依赖三视匹配元一致性度量筛选出具有低重叠率而匹配结果可靠的匹配对，这也从侧面揭示了重叠率并非是决定匹配对配准结果准确性的唯一因素，亦揭示了本文基于三视匹配元渐进式进行初值确定方法的有效性与鲁棒性．

图8 在20%重叠率阈值下本文所提初值确定方法对Dragon数据集进行初值确定的过程示意

由表2可见，在30%的重叠率阈值下，尽管OurInit相比于LRS方法精度更高，但WMA-OurInit的配准结果精度与WMA-LRS相比并无明显提高，而WMA-OurInit的效率甚至比WMA-LRS的效率低．导致WMA-OurInit方法效率较低的原因在于，OurInit的配准结果比WMA更接近真实值，即WMA-OurInit需要进行更多次迭代才能收敛到当前输入下WMA算法收敛得到的结果．WMA-OurInit算法精度无明显提高的原因在于，与25%重叠率阈值相比，在30%的重叠率阈值下，相对运动集中包含的外点数量较少，而WMA算法本身对初值选取和外点具有较好鲁棒性[9]．对比表5、表6与图7可知，随着相对运动集中外点数量的不断增加，相比于WMA-LRS，WMA-OurInit的精度、效率得到了显著提升．这是由于随着外点数量的增加，LRS的配准结果越发偏离真实值，以LRS配准结果作为输入初值的WMA-LRS算法权重因子被错误地衡量，这将导致权重因子无法真实反映出双视角匹配结果的可靠性，进一步导致精度降低甚至配准失败．较于LRS方法，由于OurInit的结果更接近于真实值，因此，WMA-OurInit算法在相对运动集存在较多外点的情况下依旧能获得较为准确的配准结果，这进一步佐证了本文所提方法的准确性与鲁棒性．

4 结 论

本文提出了一种多视角点云鲁棒配准方法，给出了方法详细的实现步骤，得到如下结论．

(2) 在获得配准初值的基础上，借助内点筛选准则，提出一种基于加权运动平均的多视角点云鲁棒配准方法．以斯坦福公开数据集为对象开展了对比实验，不同重叠率阈值下的对比实验结果表明：针对在30%、25%、20% 3种不同重叠率阈值下的相对运动集，本文所提方法均能获得较好的配准结果，证明了本文所提出方法的有效性与鲁棒性．

［1］ 张剑清，郑 莉. 基于结构光的不规则工业钣金件三维曲面重建[J]. 地理空间信息，2004(6)：9-10，19.

Zhang Jianqing，Zheng Li. 3D surface reconstruction of irregular industrial sheetmetal parts based on structure illumination[J]. Geospatial Information，2004(6)：9-10，19(in Chinese).

［2］ 徐思雨，祝继华，姜祖涛，等. 无序多视角点云的自主配准方法[J]. 西安交通大学学报，2018，52(11)：134-141.

Xu Siyu，Zhu Jihua，Jiang Zutao，et al. An automatic approach for multi-view registration of unordered range scans[J]. Journal of Xi’an Jiaotong University，2018，52(11)：134-141(in Chinese).

［3］ Besl P J，Mckay H D. A method for registration of 3-D shapes[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence，1992，14(2)：239-256.

［4］ Chetverikov D，Stepanov D，Krsek P. Robust Euclidean alignment of 3D point sets：The trimmed iterative closest point algorithm[J]. Image and Vision Comput-ing，2005，23(3)：299-309.

［5］ Govindu V M，Pooja A. On averaging multiview relations for 3D scan registration[J]. IEEE Transactions on Image Processing，2013，23(3)：1289-1302.

［6］ Guo R，Zhu J，Li Y，et al. Weighted motion averaging for the registration of multi-view range scans[J]. Multimedia Tools and Applications，2018，77(9)：10651-10668.

［7］ Li Z，Liu J，Tian Z，et al. Adaptive weighted motion averaging with low-rank sparse for robust multi-view registration[J]. Neurocomputing，2020，413：230-239.

［8］ Arrigoni F，Rossi B，Fusiello A. Global registration of 3D point sets via LRS decomposition[C]// 14th European Conference on Computer Vision. Berlin，Germany，2016：489-504.

［9］ Zhu J，Hu J，Lu H，et al. Robust motion averaging under maximum correntropy criterion[C]//2021 IEEE International Conference on Robotics and Automation (ICRA). New York，USA，2021：5283-5288.

［10］ 于靖军，刘辛军，丁希仑，等. 机器人机构学的数学基础[M]. 北京：机械工业出版社，2008.

Yu Jingjun，Liu Xinjun，Ding Xilun，et al. Mathematic Foundation of Mechanisms and Robotics[M]. Beijing：China Machine Press，2008(in Chinese).

［11］ Barfoot T D. State Estimation for Robotics[M]. Cambridge：Cambridge University Press，2017.

［12］ Zach C，Klopschitz M，Pollefeys M. Disambiguating visual relations using loop constraints[C]// 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Los Alamitos，USA，2010：1426-1433.

［13］ Hartley R，Aftab K，Trumpf J. L1 rotation averaging using the Weiszfeld algorithm[C]//24th IEEE Conference on Computer Vision and Pattern Recognition. New York，USA，2011：3041-3048.

［14］ Turk G，Levoy M. Zippered polygon meshes from range images[C]// Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques. New York，USA，1994：311-318.

［15］ Li Z，Zhu J，Lan K，et al. Improved techniques for multi-view registration with motion averaging[C]// 2014 2nd International Conference on 3D Vision. New York，USA，2014：713-719.

［16］ Lei H，Jiang G，Quan L. Fast descriptors and correspondence propagation for robust global point cloud registration[J]. IEEE Transactions on Image Processing，2017，26(8)：3614-3623.

［17］ Zhu J，Guo R，Li Z，et al. Registration of multi-view point sets under the perspective of expectation-maximization[J]. IEEE Transactions on Image Processing，2020，29：9176-9189.

Robust Approach for the Registration of Multi-View Point Sets Based on Weighted Motion Averaging

Liu Haitao，Huang Yugeng，Xiao Juliang，Yue Wei

(Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300354，China)

This study proposes a method for improving the registration performance of multi-view point sets based on weighted motion averaging. First，the relative motions of scans is estimated utilizing a pair-wise registration algorithm. Subsequently，a novel method for hierarchically estimating the initial global motions using the cycle consistency of triplets was described. This method calculates the consistency of all triplets in the view-graph of motions and gradually selects the reliable triplets for the initialization and expansion of nodes，avoiding the failures of motion averaging caused by improper initialization. With access to the accurate initial global motions，it filters outlier edges by evaluating the reliability of pair-wise registration results. Therefore，the final relative motions，as the input to the algorithm for weighted motion averaging，is the inlier subset of the initial relative motions. A comparative experiment was performed on the Stanford 3D scanning repository. Using the pair-wise registration algorithm，we obtain 12 relative motions for four range scans with overlap percentage thresholds of 30%，25%，and 20%. Among these，the error in relative motions increases when the overlap percentage threshold is decreased. The experimental results on these relative motions demonstrate that the proposed method improves the performance and robustness of the weighted motion averaging algorithm for multi-view registration. Experimental results reveal that the proposed method can obtain accurate registration results even when the set of the relative motions contains a high number of outliers，which verified the robustness of our method.

multi-view point sets registration；weighted motion averaging；cycle consistency；hierarchy

10.11784/tdxbz202202007

TP391

A

0493-2137(2023)07-0690-12

2022-02-14；

2022-05-16.

刘海涛（1981—  ），男，博士，教授.

刘海涛，liuht@tju.edu.cn.

国家自然科学基金资助项目(91948301).

Supported by the National Natural Science Foundation of China(No. 91948301).

(责任编辑：王晓燕)