基于改进型NSGA-II算法的晋中市水资源优化配置
朱思峰,李子胥
(天津城建大学计算机与信息工程学院,天津 300384)
0 引 言
我国水资源呈现时空分布不均,人均占有量小等特点[1]。由于水资源的自然因素、经济因素以及全球气候变化等自然问题的综合影响,我国面临着水资源供应不足、水环境污染、水生态退化以及极端与突发事件频繁等突出的问题。为了实现可持续发展,需要对区域水资源进行科学合理的优化配置[2]。
在水资源总量有限的前提下,通过对水资源进行优化配置,可以更好地满足社会用水需求。目前,水资源优化配置成为了一个研究热点,引起了许多学者的关注。对于复杂的水资源优化配置问题,传统的数学方法难以求解,出现了许多基于启发式智能算法的水资源优化配置方案:文献[3]通过使用快速非支配排序策略和增加拥挤度比较算子来改进飞蛾火焰算法,并在三亚市的水资源配置模型中得到了缺水量最小的决策方案;文献[4]通过增加Logistic映射和惯性权重来改进鲸鱼算法,收敛速度和精度有明显提升,并应用于邯郸市的水资源优化配置模型中,得到了以缺水量最小为特殊偏好的解集;文献[5]采用模拟退火粒子群算法从各用户配水量、缺水程度、配置目标及模型精度等多方面进行分析,得出了陕西省大荔县各子区域在不同条件下水资源优化配置结果;文献[6]采用基于改进MFO算法求解水资源优化配置,通过自适应权重表示改进MFO算法中的烛火,以自适应权重数值越小为模型最优解,得到了净收益率更高的水资源优化配置解集;文献[7]通过使用有并行机制和全局优化特性的遗传算法,将水资源优化配置问题建模为生物进化问题,通过种群间的优胜劣汰生成最优解集,以完成水资源的优化配置;文献[8]通过使用多智能体Q-学习算法将城市不同区域的用水户抽象为基于agent的模型,同时采用了一种自适应的奖励值函数来提高多智能体Q学习算法的性能以处理城市水资源配置中的各种情况;文献[9]从惯性因子及学习因子选择、外部档案维护和全局最优选取策略3个方面改进了多目标粒子群算法,并对宿迁市水资源优化调度进行实例研究,得到了分布性更好的解集。
上述这些文献大多是通过使用智能优化算法对水资源优化配置模型进行求解,为水资源优化配置提供了全新的思路。第二代非支配排序遗传算法(Non-Dominated Sorted Genetic Algorithm-II,NSGA-Ⅱ)是当前解决多目标优化问题最有效的方法之一[10]。NSGA-Ⅱ算法是 Srinivas和 Deb于2000年在NSGA 的基础上提出的[11],它具有良好的收敛性和分布性,在许多领域被广泛应用,并有很好的表现。但NSGA-Ⅱ没有考虑个体拥挤度相同时的情况,同时未考虑淘汰某个个体后相邻个体拥挤度变化造成的影响,因此提出了采用一种新型的拥挤度计算策略和一种动态的拥挤度计算方式的改进型NSGA-Ⅱ算法(简称为INSGA-II算法),并把其应用于求解建立的水资源优化配置模型。得到的非支配解集可以为多目标优化配置提供可选的解决方案,同时可为区域水资源的可持续发展提供决策依据。
1 区域概况
山西水资源十分贫乏。据数据统计,山西省人均水资源在全国列为倒数第二位。以1984年所统计的人口耕地面积计算,山西地区人均占水量466 m3,占全国人均占水量的18.8%,山西地区单位面积平均水量占全国的8%~10.9%,与南方各省相比差距较大,这足以说明山西水资源问题极其严峻[12]。
研究区域为山西省晋中市南部,行政区域划分为3个子区,分别为G1子区(平遥县)、G2子区(榆社县)、G3子区(左权县),依次对应k=1,2,3;共有3种水源,分别为地表水、地下水及引调水,依次对应i=1,2,3;共有5种用户,分别为生活用水、农业用水、第二产业用水、第三农业用水和生态用水,依次对应j=1,2,3,4,5。以最小区域内的缺水量和最大化供水经济效益为目标,建立了晋中南部供水区水资源优化配置模型。晋中市南部水资源配置网络图如图1。
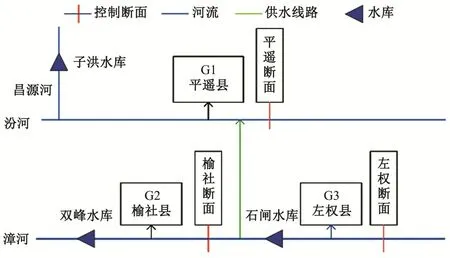
图1 晋中市南部水资源配置网络图Fig.1 Water resources allocation network in the south of Jinzhong City
以2025年为规划水平年,在来水频率P=75%下进行水资源的优化配置,以满足缺水量最小化和经济效益最大化的目标。依据晋中市的发展规划,环境最小需水量通过参考10年来枯水月的平均流量来计算,然后对不同子区内的5类用水户的需水量进行预测,不同子区内的用水户的需水量预测结果[13]如表1所示。

表1 晋中市子区2025年需水量预测 万m3Tab.1 Water demand forecast of Jinzhong sub district in 2025
考虑到实际情况中晋中市的可供水总量的不确定性、不同年份来水频率不同和晋中市近期的实际调水工程布置政策,对2025年晋中市不同子区在来水频率P=75%的情况下的可供水量进行预测[13],预测结果如表2所示。

表2 晋中市子区2025年供水预测结果 万m3Tab.2 Forecast results of water supply in 2025 for southern Jinzhong water supply area
2 水资源多目标优化配置模型
多目标水资源优化配置模型是综合考虑社会效益和经济效益,对区域内水资源进行合理有效的配置,提高区域内水资源的利用率的模型。模型将社会效益和经济效益作为目标函数、对用水户的供水量作为决策变量进行优化,其中社会效益函数用所有子区K用水户J的需水量减去所有子区K的水源对用水户J的供水量之和来表示,目标函数取缺水量(下同)最小值。经济效益函数为用水户J用水产值和用水费用之差,目标函数取最大值。
2.1 目标函数的建立
水资源优化配置的目标是使区域内的水资源配置的缺水量最小、经济效益最大。将晋中市南部区域分为3个子区,设第k(1≤k≤3)个子区有3个水源,5个用水户。决策向量其中表示第i(1≤i≤3)个水源可为子区k的j(1≤j≤5)用水户提供的水量。
(1)社会效益目标函数。以缺水量最小来满足社会效益目标函数,设第k(1≤k≤3)个子区的第j(1≤j≤5)个用水户的需水量用来表示。
社会效益目标函数计算公式如下式(1)。
(2)经济效益目标函数。以某区域用水户能够产生的最大经济效益来表示,bkj和ckj为第k(1≤k≤3)个子区的第j(1≤j≤5)个用水户的供水产值系数和供水费用系数,第i(1≤i≤3)个水源的供水次序系数用来表示,第k(1≤k≤3)个子区的第j(1≤j≤5)个用水户的用水公平系数为。经济效益目标函数如式(2)。
2.2 约束条件
(1)供水量约束。不同水源对不同子区的不同用户的供水量不超过其最大供水能力,供水量约束如式(3)、(4)和(5)所示。
式中:W1、W2、W3是三类水源分别对五类用水户的可供水量。
(2)需水量约束。区域内的水源要满足各用户的需水量要求,但不能供水过多导致浪费,所以各水源供给量既要大于或者等于各用户对各水源的最小需要量,也要小于或者等于各用户对各水源的最大需水量,需水量约束如式(6)。
(3)非负约束。所有变量都应满足大于等于零的要求。在该模型中均为已知量。
2.3 模型中的参数
(1)供水效益系数bkj。通过分析DB14/T 1049.1-2015《山西省用水定额》和产值较高的一些用水部门的用水量,得出了晋中市不同行业的生产总值和用水量的比例系数,以确定生活用水、农业用水、第二用水、第三产业用水和生态环境用水的供水效益系数。供水效益系数取值如下:生活用水为600 元/m3,第二产业用水为480 元/m3,第三产业用水为450 元/m3,生态环境用水 300元/m3,农业用水为15 元/m3。
(2)供水费用系数ckj。通过分析晋中市2016年水费征收标准和相关水价政策,以确定生活用水、农业用水、第二用水、第三产业用水和生态环境用水的供水费用系数。供水费用系数取值如下:生活用水3.90 元/m3,农业用水0.25 元/m3,第二产业用水4.58 元/m3,第三产业用水5.76 元/m3,生态环境用水2.59元/m3。
(3)供水次序系数。由于晋中南部的第二产业较多,为了防止煤炭开采和金属冶炼等产业对地下水的过度使用和污染,在水资源分配中应减少对地下水的使用,增加获取和保护较容易的地表水的使用,因此本模型的供水次序为地表水、引调水、地下水。采用式(7)计算各类水源的供水次序系数,得到结果为0.50,0.33,0.17。
式中:子区k中水源i的供水次序号用表示表示其最大值。
(4)供水公平系数。本模型通过分析晋中南部各类用水户的需求和影响,得到各用水户获水次序为生活用水、生态用水、农业用水、第二产业用水、第三产业用水,根据公式(7),得到生活、生态、农业、第二产业、第三产业对应的供水公平系数为0.33,0.27,0.20,0.13,0.07。
3 INSGA-II算法的设计
3.1 NSGA-II算法的基本原理
传统NSGA-II算法依据个体间的支配关系将种群分为若干层,将进化群体的非支配个体集合设置为第一层,将去掉第一层个体后的种群中所求得的非支配个体集合设置为第二层,将去掉第一层和第二层个体后的种群中所求得的非支配个体集合设置为第三层,以此类推,然后计算每个个体的拥挤距离。NSGA-II算法的选择操作首先对个体所在层的次序和拥挤距离进行比较,从中选择出最优个体形成新的父代种群;接着使用遗传算法产生新的子代种群,最后将新的父代种群与子代种群合并,进行基本的遗传操作,反复执行,在满足新进化种群的大小要求后停止操作[11]。
3.2 改进INSGA-II算法
对NSGA-II算法进行了改进,并把改进后的NSGA-II算法称为INSGA-II算法。改进思路是:通过改进拥挤度的计算方式和使用动态拥挤度来解决拥挤度相同时应该删除哪个个体的问题,同时在删除拥挤度最低的解后更新相邻个体的拥挤度,以此来保证种群的多样性。提出的INSGA-II算法从以下两个方面对NSGA-II算法进行了改进。
(1)左右拥挤度。在NSGA-II算法中,若两个个体的拥挤距离相等,在依据拥挤距离删除个体时无法判断该删除哪一个个体。举例,如表3。

表3 拥挤距离表Tab.3 Congestion distance table
表3为6个个体在单目标函数下的拥挤度值,按照NSGA-II算法的规则,根据公式(8)可得个体3的拥挤距离为P[4]-P[2],个体4的拥挤距离为P[5]-P[3],这两个个体的拥挤距离相等。
式中:P[i]distance为个体i的拥挤距离;P[i]fk为个体i在子目标上fk上的函数值。
在依据拥挤距离删除个体时就无法判断该删除哪一个个体,NSGA-II算法将会随机选择一个个体删除[14]。为了避免这种问题的发生,设计的INSGA-II算法采用了一种新的左右拥挤度指标:首先初始化每个个体的拥挤度,给边界节点的拥挤度赋予最大值保证其能入选下一代,对非边界节点给其添加左拥挤度P[i]distance-front和右拥挤度P[i]distance-after并初始化为0,在对子目标m的函数值排序后,依次计算非边界节点的左拥挤度和右拥挤度,最后根据左拥挤度和右拥挤度计算节点的拥挤度。具体计算方法如下:

(2)动态拥挤度排序策略。原始NSGA-II算法通过以个体的Pareto分层数和个体拥挤度为依据来选择优秀个体,在同一Pareto分层中,拥挤度是选择和淘汰个体的关键因素。但实验分析,通过使用固定拥挤度所得到的个体排序方法存在不足,当某个区域聚集了拥挤度低的个体时,固定拥挤的排序策略可能会将该区域的全部个体被淘汰,使最终得到的Pareto解集的多样性变差[15]。
在实际应用中,当某个个体被淘汰后,与之相邻的个体拥挤度将发生变化,而用固定拥挤度排序法将会忽略这一点变化,所以会导致解集多样性变差。
为了克服固定拥挤度排序法在实际应用中的不足,设计的INSGA-II算法使用一种动态拥挤度排序策略:当算法需要从种群第Fn层的h个个体中淘汰拥挤度最小的个体时,使用动态拥挤度排序策略,在淘汰之后记录该解的位置i,并且重新计算位于i+1和i-1的解的拥挤度,根据更新后的拥挤度排序来删除拥挤度最小的解,直到解集中解的数量满足要求为止。
以不同拥挤度策略在标准测试函数MOP2上的表现为例,其中种群个数为8,使用固定拥挤度排序策略的解的分布情况如图2,使用动态拥挤度排序策略解的分布情况如图3。
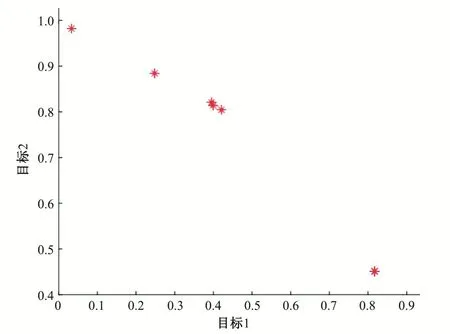
图2 使用固定拥挤度排序策略的解分布情况Fig.2 Distribution of solutions using fixed congestion sorting strategy

图3 使用动态拥挤度排序策略的解分布情况Fig.3 Distribution of solutions using state congestion ranking strategy
对比图2与图3可以看出:采用固定拥挤度排序策略进行非支配解筛选得到的解疏密不一,采用动态拥挤度排序策略进行非支配解筛选得到的解分布性更好,证明通过使用动态拥挤度的排序策略得到的种群的多样性更优。
3.3 INSGA-II算法的流程
INSGA-II算法的流程如下:
步骤1:初始化种群。根据约束条件随机产生规模为N的初始种群Pt(t=0),Qt=∅。对每个个体作函数评价,并依次对种群中的个体进行快速非支配排序、动态拥挤度计算。
步骤2:选择父代种群。对P0中的个体所在层的次序和拥挤距离进行比较,从中选择出最优个体形成新的父代种群。
步骤3:生成子代种群。对父代进行交叉和变异,产生新的子代种群Qt。
步骤4:混合父代和子代种群,形成新种群Rt=Pt∪Qt。
步骤5:选择。依据中间种群快速非支配排序的分层数和本文使用的动态拥挤度排序的方式选择优秀个体加入种群Pt+1。
步骤6:终止条件。令t=t+1,若t大于最大迭代次数MaxGen,则算法终止,同时令Pt中非支配解集作为Pareto最优解集; 若t小于最大迭代次数MaxGen,则返回步骤2。
3.4 算法测试
采用Zitzler 和 Deb[16]所列举的6 个测试函数ZDT1、ZDT2 、ZDT3 、ZDT4、ZDT5和ZDT6来验证INSGA-II算法的性能。这6个测试函数见表4,它们的Pareto前沿包含了连续、非连续、凸函数、凹函数等不同情况,这些测试函数可以科学有效地反映算法的性能,得到的测试结果也更加全面。

表4 测试函数Tab.4 Test functions
多目标优化问题通过使用收敛帕累托最优解集来获得解,并需要解保持多样性。选取两个性能指标来评价多目标优化算法得到的帕累托最优解集。
(1)反世代距离评价指标(Inverted Generational Distance,IGD)。IGD主要通过将Pareto前沿上的个体到算法获取的Pareto最优解集之间的最小距离进行求和,来对算法的综合性能包括收敛性和分布性进行评价,其计算公式如式(9)。IGD越小,表示算法的收敛性和分布性越好。
式中:P为分布在Pareto面上的个体;|P|为分布在Pareto 面上的个体的数量;Q为算法获取的Pareto 最优解集;d(v,Q)为P中个体v到种群Q的最小欧几里得距离。
(2)间距指标(Spacing Metric) 。Spacing的计算公式如式(10)。
式中:dp表示两个连续帕累托前沿之间的欧几里得距离;表示dp的平均值;表示算法所得Pareto前沿与理想Pareto前沿之间的欧几里得距离;Spacing值的大小表示Pareto前沿分布情况,Spacing值越小说明算法所得的Pareto前沿分布更加均匀。
采用的测试函数的种群大小设置为200,算法最多迭代1 000次,采用IGD和Spacing两个指标来评价计算得到的帕累托前沿的优劣[17]。各个对比算法在测试函数上的IGD值如表5所示。
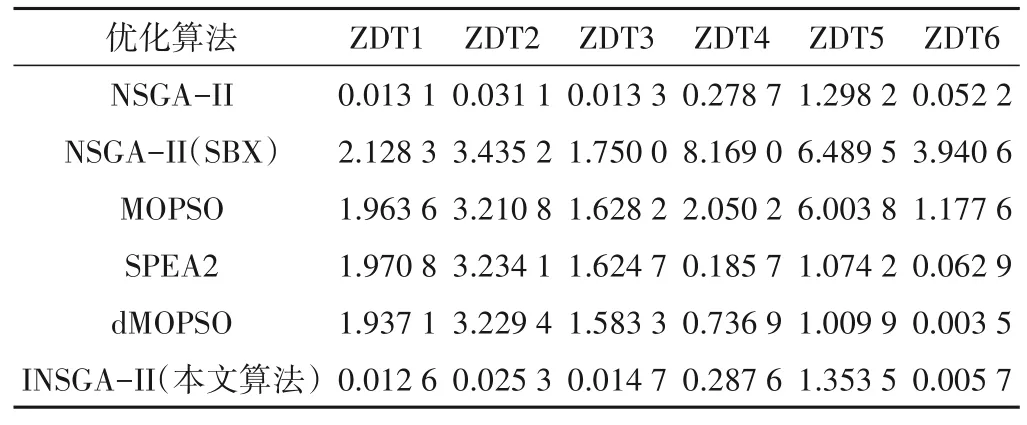
表5 不同优化算法的IGD值Tab.5 IGD values for different optimization algorithms
从表5可以看出:通过将INSGA-II算法和NSGA-II、NS‐GA-II(SBX)、MOPSO、SPEA2、dMOPSO算法进行比较[18],在测试函数ZDT1和ZDT2中,INSGA-II算法计算得到的IGD值比其他对比算法更小,在测试函数ZDT5中表现不如原始的NSGAII算法,对于其余测试函数,INSGA-II算法计算得到的IGD值处于次优。这说明本文所提出的INSGA-II算法在求解凸、非凸和离散的多目标优化问题时能够找到真正的帕累托前沿,并且具有良好的收敛性和分布性。将提出的改进算法运用于多目标水资源优化配置模型的求解,有利于高效精准地获得最优调配方案
各个对比算法在测试函数上的Spacing值如表6所示。

表6 不同优化算法的Spacing值Tab.6 SpacingValues of different optimization algorithms
从表6可以看出:通过将INSGA-II算法计算得到的Spacing值与 NSGA-II(SBX)、MOPSO、SPEA2、dMOPSO算法进行比较[18],在测试函数 ZDT1、ZDT2和 ZDT3中,INSGA-II算法计算得到的Spacing值比其他对比算法更小,在ZDT4、ZDT5和ZDT6中,INSGA-II算法计算得到的Spacing值均较优,这说明所提出的INSGA-II算法在求解凸、非凸和离散的多目标优化问题时所得到的帕累托前沿分布较均匀。在求解多目标水资源优化配置模型时,使用本文提出的改进算法有利于得到分布更均匀的优化调配方案。
综上所述,INSGA-II算法在解决多目标优化问题时能够有效得到帕累托前沿,其IGD和Spacing值要优于其他对比算法。
4 优化配置方案
使用INSGA-II算法求解晋中市水资源优化配置模型,并通过MATLAB进行编程,算法参数设置如下:种群大小为50,最大迭代次数为400,交叉概率为0.7,个体间变异概率为0.4,共得到非支配解集的个数为50。迭代次数为400时,INSGA-II算法和NSGA-II算法非支配解集对比如图4。因为提出模型中的子目标相互冲突,子目标同时达到最优值相当困难,只能通过合理分配使其向最优方向优化,即多目标问题得到的是一个非支配解集(其中一个解代表一种配置方案)。
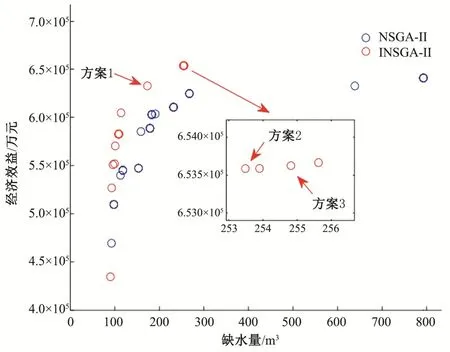
图4 INSGA-II算法和NSGA-II算法非支配解集对比Fig.4 Comparison of non dominated solution set between INSGA-II and NSGA-II
由图4可知:在迭代次数为400时,基于INSGA-II算法的水资源优化配置方案得到的非支配解集更符合要求,即解集向缺水量减小和经济效益增大的方向收敛,其中部分解集得到的经济效益更高、缺水量更小,证明使用的INSGA-II算法在求解晋中市水资源优化模型时有更好的收敛性和分布性。
在确定社会效益和经济效益两目标时,采用主观赋权法,构造公式如式(11)。
式中:x表示不同的水资源配置构成的决策变量;h表示目标个数;f1(x)表示社会效益函数,f2(x)表示经济效益函数;ωh表示目标对应的权重系数,权重之和为1。
根据对两目标需求的不同赋予不同的权重,最终得到3种方案如下。
方案1:优先最大程度满足供水,再考虑经济效益,得到该方案的多目标综合权重Ω=(ω1,ω2) =(0.8,0.2)。水资源分配方案见表7。

表7 方案1的水资源分配方案Tab.7 Water resources allocation scheme of scheme 1
方案2:同时考虑经济效益和社会效益,得到该方案的多目标综合权重Ω=(ω1,ω2)=(0.5,0.5)。水资源分配方案见表8。
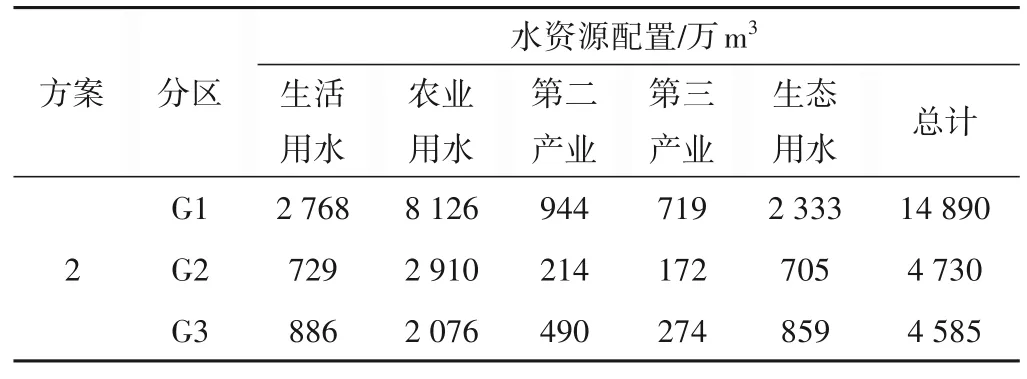
表8 方案2的水资源分配方案Tab.8 Water resources allocation scheme of scheme 2
方案3:优先考虑经济效益,再满足社会效益,得到该方案的多目标综合权重Ω=(ω1,ω2) =(0.2,0.8)。水资源分配方案见表9。

表9 方案3的水资源分配方案Tab.9 Water resources allocation scheme of scheme 3
3种方案的社会效益(缺水量)和经济效益比较见表10。

表10 3种水资源配置方案的效益比较Tab.10 Benefit comparison of three water resources allocation schemes
从表10可看出:方案1是偏好社会效益的方案,其缺水量最低(社会效益最高);方案2是均衡方案,该方案同时兼顾了社会效益和经济效益,其社会效益和经济效益值都居中;方案3是偏好经济效益的方案,其经济效益值最高。决策者可以在实际情况中根据不同的情况选择不同的方案,为晋中市水资源优化配置提供了全新的思路。
5 结 语
提出了一种使用新型拥挤度的计算策略和使用动态拥挤度的INSGA-II算法。同时分析晋中南部水资源状况,综合考虑社会效益和经济效益,构建了晋中南部水资源优化配置模型,并将INSGA-II算法应用于晋中南部水资源优化配置模型中,得到了缺水量最小和经济效益最大的非支配解集。该解集可以为晋中南部地区水资源的优化配置提供多种可选的解决方案,同时可为晋中市南部地区水资源的可持续发展提供决策依据。该配置结果同时考虑了社会效益和产生的经济效益,在解决晋中市南部水资源优化配置模型的同时,为其他地区的水资源优化配置模型的求解提供了新的思路。本文未收集污染数据,同时在经济效益函数中确定供水效益和费用系数时没有考虑不同用水户的分摊情况,待相关数据收集完整后应在水资源优化配置模型中加入生态环境效益函数,并且在经济效益函数中考虑分摊情况。通过INSGA-II算法将水质和水量分配相联系、以及在更大区域内多约束条件下的水资源优化配置问题,同时对以社会、经济及生态环境效益为目标的多目标水资源优化配置模型进行求解。

