分形：惊艳世界

万广磊 摘编

分形不仅美，能引起“极度的舒适感”，而且蕴藏着高深的数学奥秘。今天，咱们来研究研究，到底什么是分形。

分形的猜想

20 世纪初，英国数学家刘易斯·弗莱·理德查森在研究海岸线的时候，第一次发现了分形的奥秘。他发现，一条海岸线的长度不是绝对的，它取决于你用什么样的尺子来测量。考虑到海岸线被冲刷成不规则图形，你采用的测量仪器越精密，这条海岸线就越长。这就产生了一个悖论：有限的面积，却有着无限的周长。

1904 年，瑞典数学家科赫提出：取一个三角形（虽然没有规定，但通常默认为是正三角形），在每一条边的两个三等分点之间，接上一个边长只有其三分之一的小三角形。如此无限循环，最终可以得到雪花的形状。这就是著名的科赫三角形，或者叫作科赫曲线。

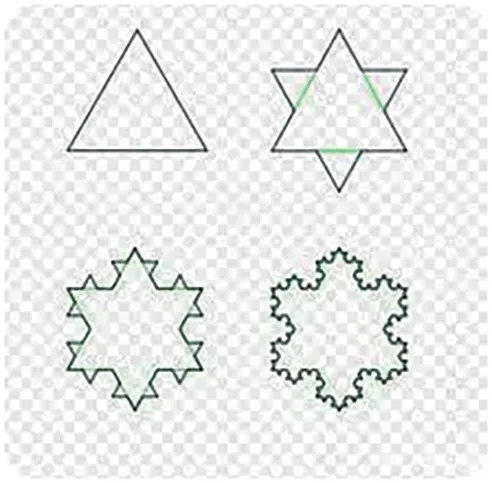
和科赫三角形正好相反，波兰数学家谢尔宾斯基在1915 年提出的谢尔宾斯基三角形，则是将小三角形放在了内部。

直到1975 年，芒德勃罗在法兰西学院讲课时，首次提出了分形的设想。

什么是分形

分形通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”。

就像刚才说的海岸线的岩石，当你看得足够细微时，它的每一个棱角都像一座小岛的海岸线。又如科赫三角形，你看到的每一个小三角形都附着在一个更大的、同形状的三角形上，同时又被更小的三角形以同样的方式附着。这种现象，被称作自相似性。

生活中的分形

分形不仅仅是数学家们一时兴起画出来的。在自然界中，分形可以说是随处可见。

计算机软件创造的分形

利用计算机软件，不断重复简单公式的计算，就能创造出意想不到的效果。苏格兰艺术家汤姆·贝达德用计算机做出的法贝热彩蛋，外表惊艳，放大后细看，会发现其包含很多的相似结构。