踩准“节拍”方可步步为“赢”

文／班洪祥

“统计与概率”是数学中考的必考内容，其呈现形式的多样性以及考查方式的灵活性常常导致大家在此“栽跟头”。甚至很多同学拿到试题时信心满满，考完后也觉得胜券在握，但总会由于混淆概念、答题不规范等原因失分。下面，我们便通过两道例题带领大家踩准中考评分的“节拍”，在“统计与概率”的答题过程中步步为“赢”。

一、在统计题中如何踩准“节拍”

例1 为了解某校九年级学生开展“综合与实践”活动的情况，抽样调查了该校m名九年级学生上学期参加“综合与实践”活动的天数，并根据调查所得的数据绘制了如下尚不完整的两幅统计图。请根据图表信息，解答下列问题：

（1）m=________，n=________；

（2）补全条形统计图；

（3）根据抽样调查的结果，请你估计该校九年级2000 名学生中上学期参加“综合与实践”活动4天及以上的人数。

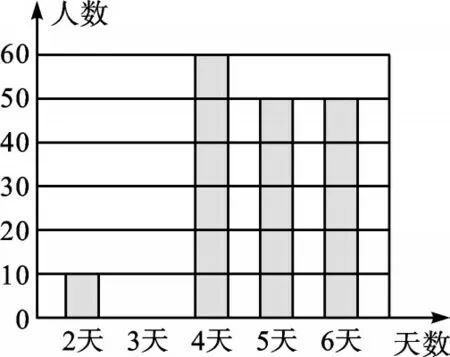
解：（1）n%=1-（15%+5%+25%+25%）=30%，n=30，m=10÷5%=200。

（2）参加“综合与实践”活动天数为3 天的学生人数为200×15%=30（名）。补全条形图如下：

（3）2000×（1-5%-15%）=1600（名）。

答：该校九年级2000 名学生中上学期参加“综合与实践”活动4 天及以上的人数约为1600名。

【点评】第（1）问在计算n时，题目已经给定了“%”，因此只需要填写数字。同学们在解答填空题时要格外留意空格后面的单位。另外，本题求m的方式有很多种，同学们应该尽量挑选小数据代入运算，这样不容易出错。本题求出m、n的值各得1分，共2分。第（2）问要先通过计算得出参与实践活动时间为3 天的人数为30 人，然后再绘制条形图，画图时注意要与其他长条等距，并在顶端标注数字，共2 分。第（3）问利用样本估计总体时要注意审题，题目强调的是4 天及以上。本题列对算式得2分，计算出结果得1分，答占1分，共4分。

二、在概率题中如何踩准“节拍”

例2 某社区举行新冠疫情防控核酸检测大演练，卫生防疫部门在该社区设置了三个核酸检测点A、B、C，甲、乙两人任意选择一个检测点参加检测。求甲、乙两人不在同一检测点参加检测的概率。（用画树状图或列表的方法求解）

解：画树状图或列表格如下。

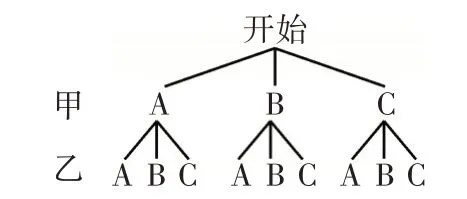
甲乙A B C AC_____________________________________BC_____________________________________CC A B________C________AA BA________CA________AB BB______________CB______________

共有9 种等可能的结果，其中甲、乙两人不在同一检测点参加检测的结果有6 种，所以P（甲、乙两人不在同一检测点参加检测）=。

【点评】此题考查的是用树状图法或列表法求概率。第一步画树状图或列表得4 分；第二步写出等可能的结果数及符合条件的结果数得2 分；第三步求事件发生情况数与总情况数之比，得出概率得1分，最后答占1分。解题时要注意此题是放回试验还是不放回试验，若同学们在理解时产生偏差，画树状图或列表就会出错，后面的每一步解答也就会跟着错，所谓一步错，步步错，最终导致失分。

“统计与概率”题看似简单，但其答题过程依旧需要规范、严谨。只要会读统计图，理清题目意思，画树状图与列表准确，计算不偏差，语言表述完整，一定能踩准得分节拍，获得满分便不是难事。