“四问”厘清概念，破解易混点

文／周 炼

专题复习 统计与概率

领衔人：钱德春（正高级教师）

组稿团队：江苏省泰州市教育局教研室

同学们之前学习“统计与概率”时是否觉得很多名词都长得十分相像，并且十分容易混淆？我们不妨对这些易混概念进行一次“全名搜查”，通过四个问题勾起同学们的学习记忆，相信你一定能在阅读本文后将“统计与概率”中的易混点一扫而空！

一、你认为哪种调查方式更合适

例1 下列调查方式，你认为最合适的是（）。

A.调查元宵节期间市场上元宵质量情况，采用普查方式

B.旅客上飞机前的安检，采用抽样调查方式

C.调查本市居民对“垃圾分类”有关内容的了解程度，采用普查方式

D.调查飞机重要零部件的产品质量，采用普查方式

【分析】普查是对所有考察对象所做的调查，抽样调查是对部分考察对象所做的调查。对具有破坏性的、无法进行普查、普查的意义或价值不大的调查，宜选择抽样调查；对于精确度要求高、事关重大的调查，宜选择普查。同学们要分清楚这两种调查方式的适用范围。

解：调查元宵节期间市场上元宵质量情况与调查本市居民对“垃圾分类”有关内容的了解程度，只需要得出近似判断，宜采用抽样调查；旅客上飞机前的安检与调查飞机重要零部件的产品质量，虽耗费人力、物力较多，但由于其精确性要求，宜采用普查。故选D。

二、你理清楚这些统计名词了吗

例2 为了解某校初一年级900 名学生每天花费在数学学习上的时间，抽取了100名学生进行调查，以下说法正确的是（）。

A.900 名学生每天花费在数学学习上的时间是总体

B.每名学生是个体

C.从中抽取的100名学生是样本

D.样本容量是100名

【分析】总体是考察对象的全体，个体是组成总体的每一个考察对象，样本是从总体中所抽取的一部分个体，样本容量是样本中个体的数目。要注意的是，样本容量仅为数字，不能带单位，同学们可不要多此一举哦！

解：900 名学生每天花费在数学学习上的时间是总体，A 正确；每名学生每天花费在数学学习上的时间是个体，B 错误；从中抽取的100 名学生每天花费在数学学习上的时间是样本，C 错误；样本容量是100，D 错误。故选A。

三、你知道频率与概率的关系吗

例3 利用六张编号为1、2、3、4、5、6 的扑克牌进行频率估计概率的试验中，同学小张统计了某一结果出现的频率，绘出的统计图如图1 所示，符合这一结果的试验可能是（）。

A.抽中的扑克牌编号是3的概率

B.抽中的扑克牌编号是3的倍数的概率

C.抽中的扑克牌编号大于3的概率

D.抽中的扑克牌编号是偶数的概率

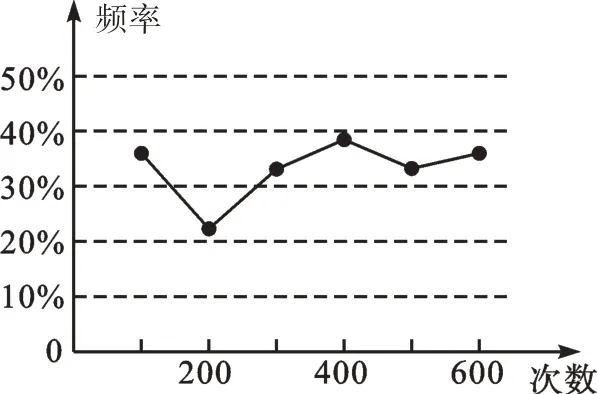
图1

【分析】在实际生活中，人们常把试验次数很多时，事件发生的频率作为其概率的估计值，但同学们千万别误把频率当作概率。当题目中给出随机事件发生频率的折线统计图时，我们可以利用图中随着试验次数增多且趋于稳定的频率值来估计概率。

四、你知道算术平均数与加权平均数的区别吗

例4 某公司招聘人员，对学历、工作经验、表达能力、工作态度四方面进行综合考核。其中一位应聘者，这四项依次得分为8分、9 分、7 分、8 分（每项满分10 分）。若将这四项的平均分记为面试综合成绩，则这位应聘者的得分为________；若按照如图2 所示的比例确定面试综合成绩，则这位应聘者最后的得分为。

图2

【分析】将一组数据相加并除以这组数据的个数，所得结果便是这组数据的算术平均数。当给出不同数据的重要程度时，平均数还与各个数据的“权”有关，此时同学们需要练就一双识别“重要程度”的火眼金睛，学会在具体情境中灵活运用这两种平均数。

解：（8+9+7+8）÷4=8（分）；8×15%+9×25%+7×30%+8×30%=7.95（分）。