水中金属丝电爆炸动力学过程的零维模型*

薛 创，宁 成，彭先觉

（北京应用物理与计算数学研究所，北京 100094）

电爆炸丝是加载强电流脉冲的金属丝在短时间内产生大量焦耳热从而发生爆炸的实验技术[1-4]，它具有测量数据可靠、重复性好、操作简便等优点，在Z箍缩等离子体物理、爆炸力学、物性参数研究等方面有着重要应用。其中，在爆炸与冲击应用方面，Antonov 等[5]利用40 根铜丝组成的球形丝阵在水中产生了2 TPa 的高压力，Tang 等[6]采用电爆炸铜丝方法代替传统的起爆技术改善了柱面爆轰波的品质。国内早期关于电爆炸丝和电爆炸导体的实验研究是测量电压、电流等电参数[1-2]；随着诊断技术的进步，发展为测量丝边界运动轨迹、环境介质中的冲击波轨迹[3-4,7]，近年来进一步发展为测量丝等离子体的温度和密度分布[8-10]，取得了大量研究成果。

在零维理论建模方面，Tucker[11]建立了比作用量模型，采用该模型可以计算金属丝的电阻率变化和能量沉积，至今仍在实验和理论研究中发挥作用[12-13]，但基于初始半径和横截面积计算电流密度，原则上仅适用于爆炸前的过程，需要合适的模型描述丝的膨胀过程，获得随时间变化的半径。Bloomberg 等[14]建立了一个动力学模型来描述Z箍缩丝阵等离子体的形成过程，假设单丝等离子体的温度、密度和压力均匀分布，膨胀是自相似运动过程，则动能方程和内能方程可简化为两个常微分方程，采用修正的理想气体状态方程和Spitzer 电阻率作为封闭条件，能够获得半径的时间变化。郭军等[13]建立的零维模型将金属丝电爆炸过程分为膨胀前和膨胀后两个阶段，分别采用比作用量模型和动力学模型描述，其中膨胀后的动力学过程由动量方程与总能量方程描述，但能量方程形式与Bloomberg 的不同，内能及总能量转换过程中热压的贡献不同。晁攸闯等[15]建立了一个描述水中电爆炸丝的零维模型，采用了数据库形式的电导率，为了合理利用理想气体状态方程，采用了比作用量模型计算爆炸时刻的等离子体状态。Rososhek等[16]建立了一个描述水中电爆炸丝膨胀及冲击波传输的零维模型，但该模型依赖于实验测量的电功率和一个调节能量沉积和做功份额的参数作为输入条件，也采用了理想气体状态方程。

在一维理论和数值模拟方面，通常采用磁流体建模[17-18]。Chung 等[18]基于考虑液气相变的实际气体物态方程和半经验的电导率公式，给出了水中铜丝电爆炸过程的冷启动物理建模，获得了与实验数据相符合的数值模拟结果。本文基于含人工黏性的差分方法研制一维拉格朗日程序SWEET (single wire electrically exploding test)，采用实际气体状态方程QEOS[18-19]模型和修正的Lee-More[20-23]电导率模型作为封闭条件，进行金属丝电爆炸过程的冷启动数值模拟。

为了方便理解和分析水中金属丝电爆炸动力学过程和能量转化过程，本文在一维数值模拟工作基础上，依据Bloomberg 的基本假设发展了零维模型，采用实际气体状态方程和电导率作为封闭条件，采用Rososhek 的激波模型作为边界条件，进行从电容器放电到金属丝电爆炸的冷启动及连续过程计算：首先，确定零维模型的控制方程和定解条件；其次，将计算结果与一维模型以及实验结果进行比较，验证零维模型基本假设的合理性。

1 物理模型

在一维柱对称、单温、单速度、单流体和磁扩散等近似下，等离子体的质量方程、运动方程、内能方程和磁场演化方程分别为：

式中：ρ 为质量密度，v为径向速度，t为时间，r为径向位置，p为压力，j为电流密度，B为磁感应强度，ei为比内能，η 为电阻率，时间导数都是拉格朗日随体导数。

根据Bloomberg 的假设条件：密度沿径向均匀分布，除边界点外，空间偏导数为零，式(1)的左端密度不含空间位置信息，对其从0 到r积分，得到速度沿径向的分布：

即速度沿径向呈线性分布，如果丝等离子体边界半径为rp，边界速度为vp，则速度分布为：

式(5)和式(6)联立消去速度后，对时间积分的结果满足质量守恒条件。

对运动方程（式(2)）左右两边乘以2v就能得到动能方程，再对动能方程和内能方程两边求空间体积积分，消去空间导数，分别得到零维模型的动能和内能方程：

式中：m= ρSh为丝质量，S=πrp2为丝等离子体柱的横截面积，h为丝长度；e¯k=v2p/4 ，为单位质量的平均动能；p¯ 和ēi分别为平均压力和平均比内能，在压力和内能均匀分布的假设下，可以去掉上标，即p=p¯ ，ei=ēi；p0为丝等离子体边界处的压力，等于水中的激波波后压力；Rload为丝的电阻，在本文的研究范围内电流随时间的上升速率较小，趋肤深度较大，丝半径较小，电流密度均匀，因此Rload= ηh/S；I为电流强度，pB=µ0I2/(8πS)为磁压力，µ0为真空磁导率，在本文单位制下µ0= 4π。

动能方程（式(7)）可以简化为等离子体边界的运动方程：

一维模型方程组（式(1)～(4)）及零维模型方程组（式(7)和式(8)）的求解需要状态方程和电导率参数作为封闭条件，以密度、温度作为基本热力学变量，有：p=p(ρ,T)，ei=e(ρ,T)，η = 1/σ(ρ,T)，其中σ 为电导率。本文采用的铜介质状态方程和电导率参数随温度、密度的变化关系见图1。

图1 铜介质物性参数以及丝等离子体的轨迹Fig. 1 Physical properties parameters of copper and trajectory of wire plasma

图1 还给出了典型电爆炸丝等离子体的密度和温度的状态变化，可以看出从固态变为等离子体，密度变化了约4 个量级，温度变化了约3 个量级。图2 比较了电导率参数的插值公式和实验结果。

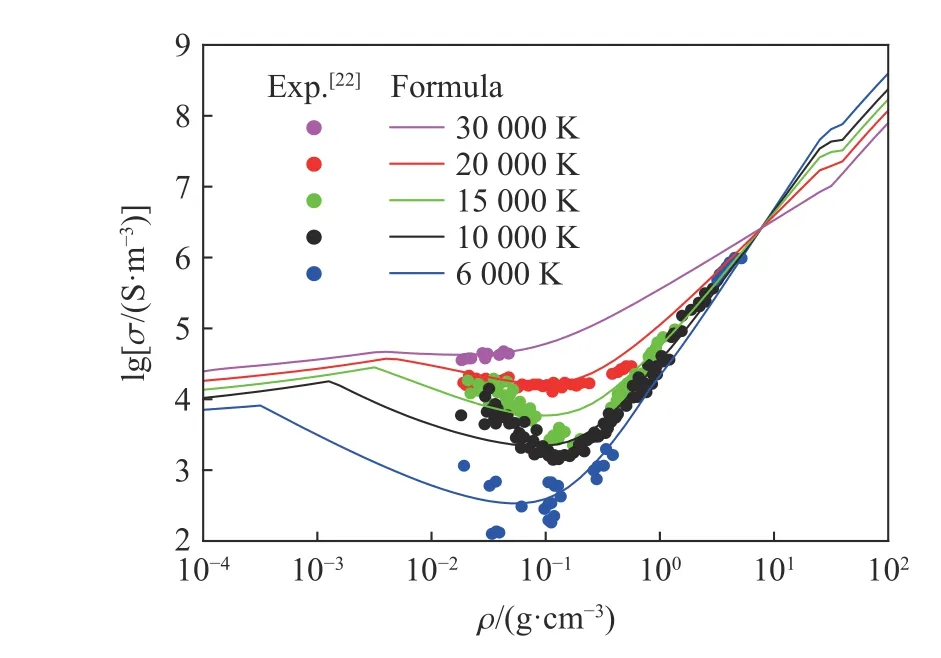
图2 铜介质的电导率参数与实验结果[22]比较Fig. 2 Comparison of the electrical conductivity for copper with experiment results[22]

计算磁压力和焦耳热还需要已知电流I，可以由实验测量得到，本文根据等效电路模型计算得到。通常，脉冲功率装置对金属丝负载放电的等效电路如图3 所示。

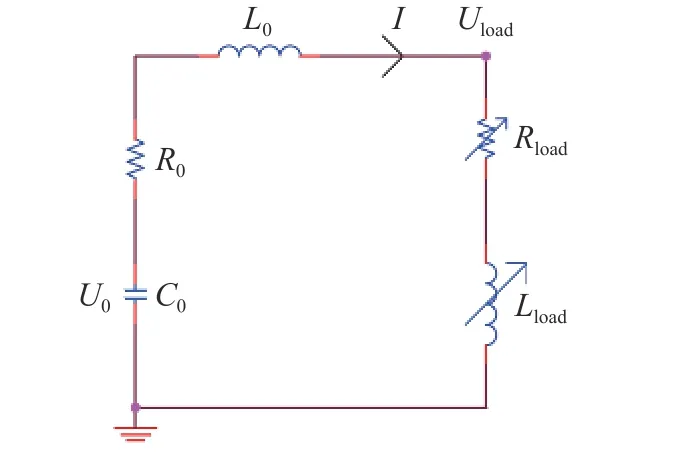
图3 电爆炸金属丝的等效电路模型Fig. 3 Circuit model for the electrically exploding wire

脉冲功率装置的等效电容为C0，初始充电电压为U0，放电过程中随时间变化的电压为Ubank，等效电阻为R0，等效电感为L0。金属丝负载的等效电感[18]为Lload= 2h[ln(2h/rp)-0.75]，负载电感和电阻都随着电爆炸过程而变化，通常在电爆炸过程中的电感变化较小，电阻的变化很大。装置电压Ubank、负载电压Uload和电流I之间满足电路方程：

水介质环境下，等离子体的膨胀受到环境介质的影响。假设边界压力p0与压缩后的水介质压力pw平衡，如图4 所示，根据波阵面的激波关系式和水介质的质量守恒条件可以获得这个边界压力。

图4 丝等离子体边界及水中激波间断示意图Fig. 4 Schematic profile of the wire plasma interface and shock wave in the water

在随激波波阵面运动的参考系中，水中激波的间断关系为：

式中：ρw0= 1 g/cm3为水的波前密度，ρw为水的波后密度；pw0为水的波前压力，pw为水的波后压力；Sw为激波波阵面的速度，vw为波后水的速度。波前状态已知，式(11)包含4 个未知量，还需要补充两个方程。第一个是水的状态方程，即压力和密度的关系为：

式中新引入了两个常数：参数n= 7.15，代表压缩性，数值越大，表示越难压缩；Cw0= 1 478 m/s，为水中的声速。第二个方程是水介质波后与丝等离子体界面位置之间的质量守恒关系：

式中：rs为激波位置，r0为丝的初始半径。联立式(11)和式(12)消去波后压力与水的速度，得到激波速度与密度之间的关系式：

式中：δ 为水的压缩比。已知等离子体位置rp，就能根据式(13)和式(14)确定激波位置和速度；而等离子体边界位置rp只需要知道式(12)的边界压力，求解控制方程（式(8)和式(9)）就能得到。

2 模拟应用

选取Chung 等[18]的水下铜丝电爆炸实验作为零维模型的应用，等效电路参数为：电容C0= 5.22 μF，装置电阻R0= 65.45 mΩ，装置电感L0= 3 050 nH，充电电压U0= 13 kV；铜丝参数为：长度h= 4 cm，初始半径r0= 25, 50, 100 μm。首先给出50 μm 半径下的基本动力学过程以及能量转化关系，对比一维磁流体程序的模拟结果和实验结果，然后改变丝参数，考察放电模式的变化。

丝等离子体的电压及电流波形是实验的直接测量量，见图5。对比时间波形、峰值、峰值时刻等特征，本文的计算结果与实验结果符合较好，而Tucker 模型[11]计算的电流在上升沿至爆炸时刻之前与本文中结果符合，爆炸时刻之后出现明显偏离。

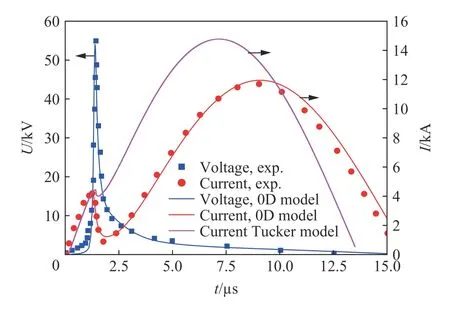
图5 电压和电流的时间演化曲线Fig. 5 Temporal evolution of voltages and currents

丝等离子体的膨胀轨迹及水中激波轨迹同样是实验关注的测量量，实验结果与零维模型结果的比较见图6。图7 在一维压力分布上叠加了丝边界运动轨迹、激波轨迹的实验数据和部分丝质点流线。总体上零维模型和一维模型均给出了与实验符合的动力学结果。由于零维模型始终以激波波后压力作为边界条件，但实际上水中的激波波后压力并非均匀，后期该边界压力偏大（如图7 所示），这导致丝等离子体的膨胀速度及激波速度偏低。

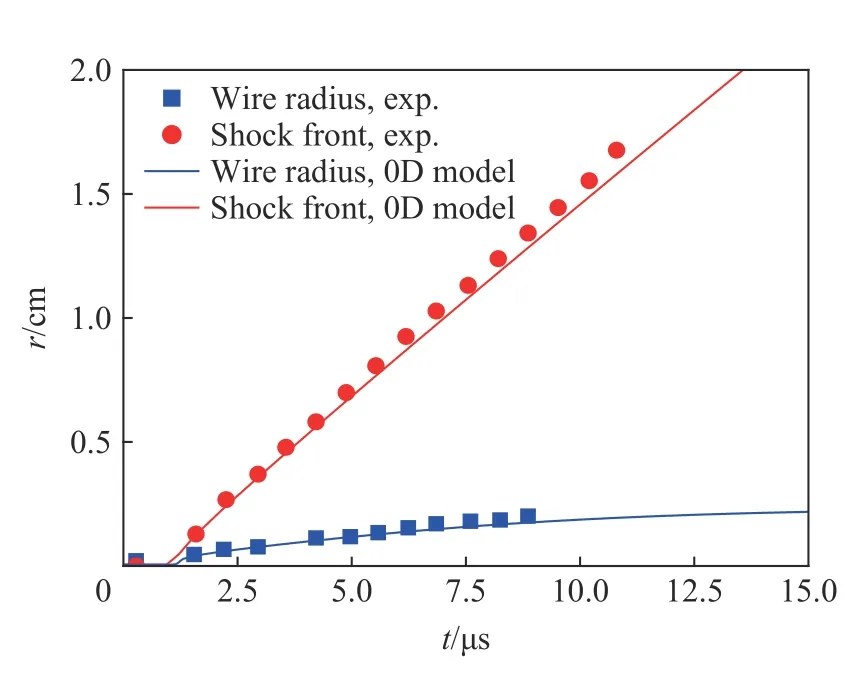
图6 等离子体边界和激波阵面的时间演化曲线Fig. 6 Temporal evolution of wire radius and shock front

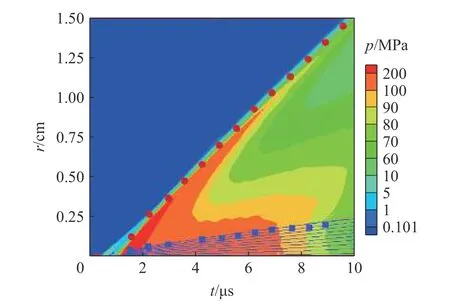
图7 丝等离子体和水介质压力分布随时间的演化Fig. 7 Pressure histories of wire plasma and water

密度和温度是零维模型的基本热力学状态量，也是压力、电阻率等其他物理量的基础，假设丝等离子体密度均匀，则根据实验测量的边界轨迹也能获得体积和密度，图8 给出了它们的时间演化曲线。对比了零维模型、一维模型及实验的密度结果，发现三者在一定范围内较符合；一维程序采用了数十个质点描述丝等离子体，它们的热力学状态在早期较长的时间内基本重合，图7 也能看出这些网格在膨胀过程中均匀分布，说明在该实验应用中零维模型的基本假设是合理的。另外，前期零维模型的温度比一维模型的更高，后期更低，说明二者的能量转化过程存在一定的差异。

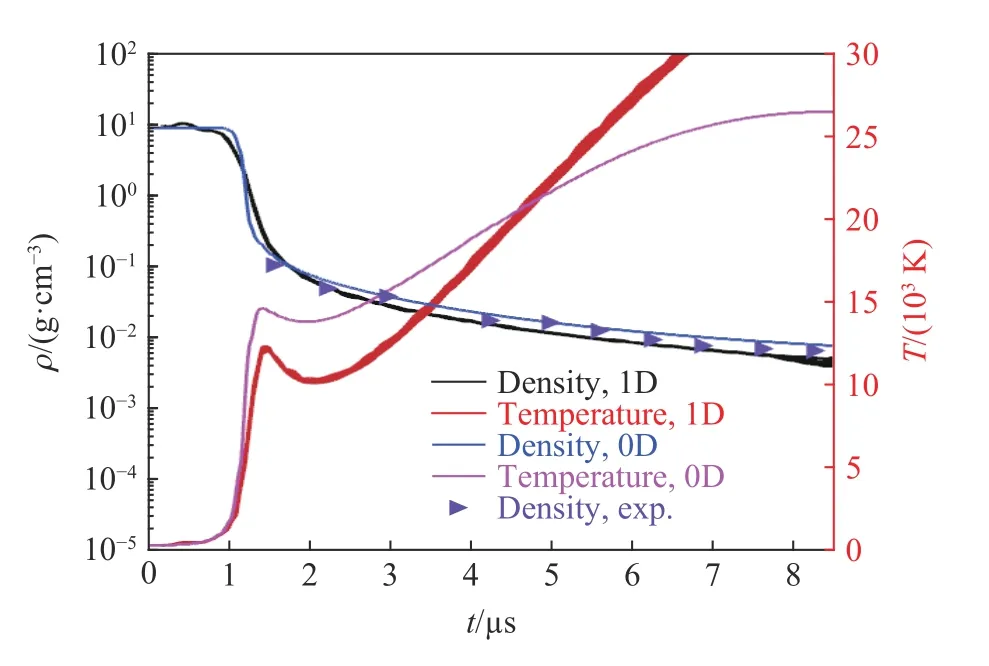
图8 等离子体密度和温度的时间演化曲线Fig. 8 Temporal evolution of density and temperature of the wire plasma

图9 给出了早期焦耳热（qJ）的沉积、热压力做功（pdV）与丝等离子体内能和动能的关系，与能量守恒关系较为吻合，与本文中式(7)和式(8)的描述完全一致。

图9 能量及其源项随时间的演化曲线Fig. 9 Temporal evolution of Joule heating, work, internal energy and kinetic energy of the wire plasma

上述结果展示了电爆炸丝等离子体的基本能量转化过程。焦耳热（qJ）提供了内能增加和温度上升的能量源，膨胀过程的做功（pdV,V为体积）会损失等离子体内能（Ei），使得温度下降；膨胀过程中的热压力克服边界水压力做功（pwdV）及磁压力做功（pBdV）是动能的源项，对于动能（Ek）与内能之和即总能量而言，焦耳热是正的源项，磁压和边界压力做功是负的源项。从数值上看，磁压力做功和丝等离子体的动能相对较小，焦耳热主要转化为内能和对水介质做功。

进一步考察本文模型与其他模型中采用的理想气体压力以及Tucker 电阻率[11]的对比，见图10。膨胀早期丝密度较大，考虑电离度修正的理想气体压力[13]（p=RρT(1+Z)/A，R为气体常数，Z为电离度，A=63.5 为铜的原子序数）将得到较大的压力；在爆炸时刻之后，根据实际气体状态方程得到的压力近似与电离度为1 的修正理想气体压力相等。在熔化时刻前，本文零维模型采用的电阻率与Tucker 模型[11]的数值完全相同，但在气化阶段产生了明显分离；爆炸时刻之后的Tucker 电阻率[11]较小，与此对应，图5的电流在第一个峰之后下降不明显，从而与实验测量的电流波形不相符。

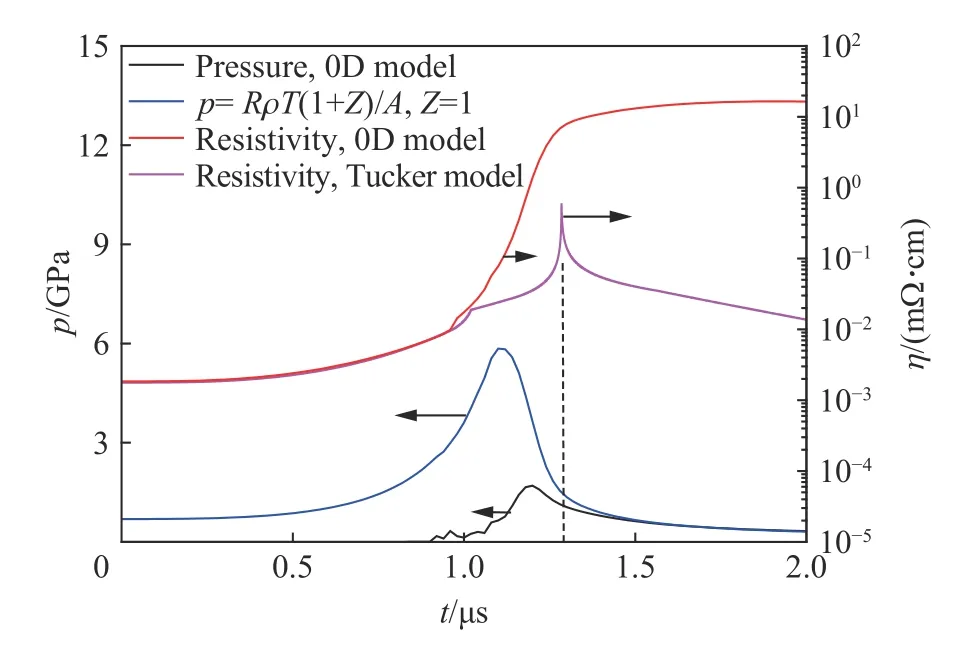
图10 压力及电阻率的时间演化曲线Fig. 10 Temporal evolution of pressure and resistivity

最后，给出丝半径变化对放电模式的影响，见图11。在固定充电电压和丝长度的情况下，增大丝半径会减小丝电阻和电感，从而减小电压峰值；同时，由于丝质量增大，升高相同的温度需要更多的焦耳热，因此电压峰值时刻推迟；电流的第一个峰值时刻也随之推迟，且第一个电流峰值更大。爆炸发生之后，电阻率在一定时间内维持较大的数值，丝电阻较大，使得电流减小，当丝半径小于某个阈值时，电流出现“停滞”，直到丝膨胀后截面积增大，丝电阻减小，电流再次增大。另外，当丝半径足够大时，由于脉冲功率源的能量有限，丝的温度不会升高到发生液气相变的温度，此时电流波形将呈现短路电流的状态。

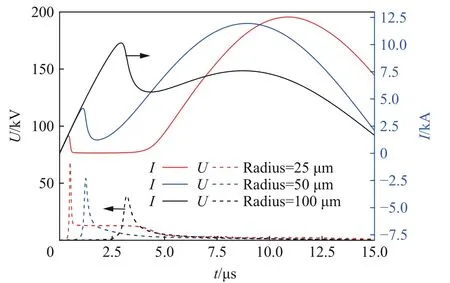
图11 丝半径改变下的电流及电压波形Fig. 11 Current and voltage waveform for wires with different radii

3 结 语

本文发展了一个描述水中金属丝电爆炸过程的零维模型，包含了动能和内能的演化方程、实际气体状态方程、修正的李-莫尔电导率参数，以及水中激波关系式等，实现了以实验室温度和密度为初始状态的冷启动和连续过程模拟计算。当采用实际气体状态方程时，初始压力远小于理想气体压力，早期不会发生非物理膨胀；当采用本文的电导率模型时，早期电阻率与Tucker 比作用量模型的结果符合较好，因此不需要将电爆炸丝过程分为熔化前和熔化后两个阶段建模。

对比分析了基于一维磁流体模型的SWEET 程序模拟结果，认为在电流上升阶段，水环境中质量密度、温度和电流密度的均匀分布假设较为合理，采用零维模型描述丝等离子体对于校验物性参数更方便。然而，当电流下降后，丝等离子体的压力可能小于水中激波的波后压力，将会产生稀疏波追赶激波的图像，零维建模的基本假设就不再满足了。尽管如此，在本文的参数范围内，零维模型的等离子体边界轨迹及激波轨迹与实验结果相符合；能量转化关系清楚，守恒性好；改变丝直径，获得了不同的放电模式，同样与实验规律相符合，证明了该零维模型的合理性。