基于爆炸切割试验的有机玻璃本构模型参数反演*

张宇卓，赵 铮

（南京理工大学能源与动力工程学院，江苏 南京 210094）

有机玻璃（PMMA）的爆炸切割在军事领域的运用广泛[1-4]，战斗机飞行员进行逃生座椅弹射时需要利用聚能切割索对飞机舱盖进行切割，潜射导弹发射前需要利用爆炸切割将发射头罩进行切割。此时，脆性板壳的被切割效果直接影响了战斗机飞行员的生命安全及潜射导弹的顺利发射。同时，在爆炸切割作用下，炸药爆炸产生的应力波和破坏相互作用会导致相当复杂的材料破坏机制。当脆性材料承受冲击和侵彻的压缩荷载作用时，在材料内部必然会激发应力波的作用。初次产生的压缩脉冲在材料的自然边界以及内部自由表面上将发生反射并且相互作用，在材料内部将产生局部拉应力，引发复杂的反射断裂模式，如层裂、角裂等。确定PMMA 的材料本构模型及其本构模型参数对于分析和研究PMMA 结构在爆炸切割载荷下的损伤情况至关重要。

常见的PMMA 本构模型有ZWT[2,5]、Drucker-Prager[6-7]等模型，其中JH-2（Johnson Holmquist ceramics）[8-9]本构模型应用较广。然而使用实验方法测定JH-2 本构模型参数需要多种试验，获得参数的成本较高[10-11]。然而本文所研究的材料参数反演方法是一种利用试验测量得到的反映材料力学行为的物理量反向推算材料本构模型参数的方法。相较于上文中的材料参数获得方法，参数反演法所需的试验更少，且获得的参数相当精确。近些年来，在参数反演的算法方面，以神经网络算法为代表的智能算法应用逐渐增多，其反演效果也被证实较为出色[12-13]。

现阶段对于材料本构模型方程参数反演的研究多集中在准静态试验或工况方面[14-15]，对于本文所研究的高围压、高加载率下材料本构模型参数的反演研究较少。茹一帆等[16]基于试件的准静态单向拉伸试验数据反演出了6005A-T5 铝合金的Johnson-Cook 模型参数；李守巨等[13]基于三轴压缩试验得到的堆石料材料应力-应变关系对堆石料材料本构模型参数进行反演；贠永峰等[12]基于隧道拱顶和拱底的宏观位移数据对岩体材料本构模型参数进行反演。在PMMA 平板爆炸切割工况数值模拟中，PMMA 的本构模型不仅反映应力应变关系，同时还决定着脆性材料断裂、破碎和裂纹扩展等损伤过程的进行，并且在实际运用中，其损伤情况是项目及研究更关注的方面，这是上述文献中未涉及的部分。因此在选择神经网络模型的损失函数时，应该对PMMA 平板的损伤情况数据有所侧重，使得参数反演的结果能够更准确地体现出爆炸切割对PMMA 平板造成的破坏。

本文将以PMMA 平板爆炸切割试验为案例，通过LS-DYNA 软件构造样本并收集数据集，使用Python 语言搭建神经网络预测模型，对PMMA 材料JH-2 本构模型参数进行反演，并将反演结果与试验结果进行对比，对反演结果的可靠性进行检验。

1 PMMA 平板爆炸切割试验

1.1 爆炸切割PMMA 平板试验介绍

选择三种PMMA 平板进行切割试验。这三种平板具有相同的密度（1.18 g/cm3）、杨氏模量（2.5 GPa）、泊松比（0.35），但冲击强度不同。依据国标GB/T 1843―2008/ISO 180:2000《塑料 悬臂梁冲击强度的测定》、采用XJJ-50 型简支梁摆锤式冲击试验机对三种PMMA 平板进行冲击强度测定，取三次测试数据平均值作为每种PMMA 平板的冲击强度值。冲击强度测试结果如表1所示。

表1 冲击强度测试数据Table 1 Testing data of impact strength

根据文献[8]给出的方法，将冲击强度转换为抗拉强度T：

式中：Ak为冲击功，E为弹性模量，v为泊松比，c为裂纹半径 ，H、L为平板材料的宽度和厚度。根据式(1)得到平板1、2、3 的抗拉强度依次为102.4、135.7 和174.9 MPa。

爆炸切割试验使用的切割索药型罩为铅锑合金，药芯装药为黑索金，该炸药起爆威力大，具有较高的爆温和爆速，且化学稳定性好，其密度为1.717 g/cm3，爆速为7 980 m/s。切割索截面如图1 所示。

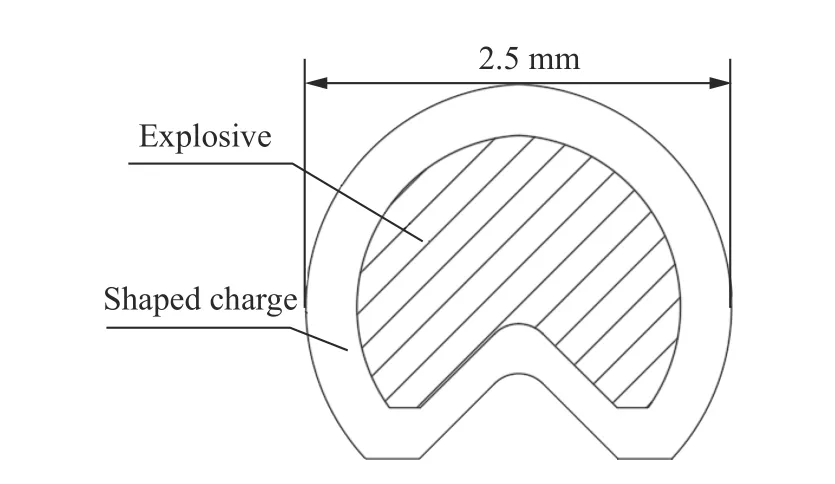
图1 切割索截面Fig. 1 Cross-section of linear shaped charge

PMMA 平板爆炸切割试验在工装上进行，将厚度为14 mm 的PMMA 平板固定在工装上，采用零炸高进行爆炸切割试验。试验准备结束后情况如图2(a) 所示，一端夹紧起固定作用，将切割索粘结在PMMA 平板上；爆炸切割后工装及平板状态如图2(b)所示。

图2 爆炸切割实验Fig. 2 Explosive cutting test

1.2 爆炸切割PMMA 平板试验结果分析

为了对PMMA 平板的损伤响应进行量化，以便使用神经网络进行处理，本文按照脆性材料损伤机理将PMMA 平板在爆炸切割作用下的损伤分为射流侵彻、冲击断裂和层裂。并且将平板断裂的厚度分为射流侵彻深度、冲击断裂厚度和层裂厚度三种损伤数据。

试验结果如图3 所示，三块PMMA 平板在爆炸切割下的损伤存在较大差异。平板1 的射流侵彻深度约3.5 mm，底部层裂厚度约5.0 mm，中部冲击断裂厚度约5.5 mm，平板被成功切开；平板2 的侵彻深度约4.7 mm，底部层裂厚度约4.5 mm，中部冲击断裂部分厚度约4.8 mm，平板同样被成功切开；平板3 射流侵彻深度约7.3 mm，不存在层裂和冲击断裂，平板并未被切开。PMMA 平板损伤数据在表2 中列出。

图3 爆炸切割试验结果Fig. 3 Explosive cutting test results

表2 PMMA 平板损伤数据Table 2 PMMA flat plate damage data

2 PMMA 平板本构模型参数反演

2.1 有限元模型建立

切割索爆炸切割PMMA 平板的有限元模型由PMMA 平板、炸药、铅锑合金药型罩以及空气域4 部分构成，药型罩尺寸如图1 所示。PMMA 平板厚14 mm，宽30 mm。为节省计算时间，采用1/2 对称模型，所有部分在对称面施加对称约束，空气域中除对称面和与z轴垂直的两个面外，其余三个面添加无反射边界条件。PMMA 平板采用Lagrange 实体网格，切割索的炸药部分及药型罩部分与空气域均采用ALE 实体网格。PMMA 平板与空气单元网格水平方向单元最小尺寸为0.07 mm。炸药、药型罩、空气域网格如图4 所示。

图4 局部有限元网格Fig. 4 Partial finite element mesh

2.2 材料参数

本文采用的炸药为黑索金，材料模型采用LS-DYNA 中的高能炸药模型，即008#材料模型（*MAT_HIGH_EXPLOSIVE_BURN），该材料模型中燃烧分数F乘以高能炸药的状态方程，可控制化学能的释放以模拟爆炸：

式中：pHE为单元在高能爆炸中的的压力，peos为由状态方程给出的压力，V为相对体积，E为单位体积炸药的初始内能。该材料模型所需参数：质量密度为1.717 g/cm3，爆炸速度7 980 m/s，C-J 压力为30.15 GPa。

式(2)中的peos由JWL 状态方程来定义：

式中：AJWL、BJWL、R1、R2、ω 为状态方程参数。

PMMA 平板采用JH-2 (Johnson Holmquist ceramics)本构模型。JH-2 本构模型是一种由强度、压力和破坏三部分组成的塑性损伤模型。本文使用该材料本构模型描述PMMA 平板的力学动态响应和损伤响应。JH-2 材料模型通过归一化压力(p*)，归一化抗拉强度(T*)和归一化总增量应变率的非线性函数进行评估。

完整的材料强度定义为：

断裂材料的强度定义为：

断裂开始之前的静水压力为：

恒定压力下破裂的塑性应变定义为：

式中：A、B、C、M、N为材料常数，即为本文需要通过反演来确定的目标参数；K1、K2、K3为状态方程常数；D1和D2为损伤常数；p*=p/pHEL，T*=T/pHEL，pHEL为Hugoniot 弹性极限处的压力分量，p为JH-2 模型中材料的真实压力，T为抗拉强度； ε˙*为归一化应变率， ε ˙*= ε˙/ε˙0，ε ˙ 为实际应变率，ε ˙0=1 s-1为参考应变率；µ=ρ/ρ0- 1，ρ 为当前密度，ρ0为初始密度。JH-2 模型中的经验参数为：A=1.9,B=2.5,C=0.001,M=0.6,N=0.6；平板的密度、杨氏模量、泊松比和抗拉强度见1.1 节。

2.3 参数反演

本节首先以经验参数为基准确定PMMA 平板参数调整区间，见表3。使用LS-DYNA 软件对PMMA 爆炸切割过程进行多次有限元数值模拟以收集用于训练神经网络模型的数据集，数据集共有62 组数据。训练神经网络时使用的数据集输入值为三种平板的侵彻深度（h1、h2、h3）、冲击断裂厚度（d1、d2、d3）和层裂厚度（δ1、δ2、δ3），分别代表相同本构模型参数下三种有机玻璃平板在爆炸切割数值模拟下的损伤情况。输出值为五个本构模型参数：A、B、C、M、N。数据集的输入值和输出值的格式见表4 和表5。

表3 PMMA 平板JH-2 本构模型参数调整区间Table 3 Adjustment interval of parameters of PMMA flat plate JH-2 constitutive model

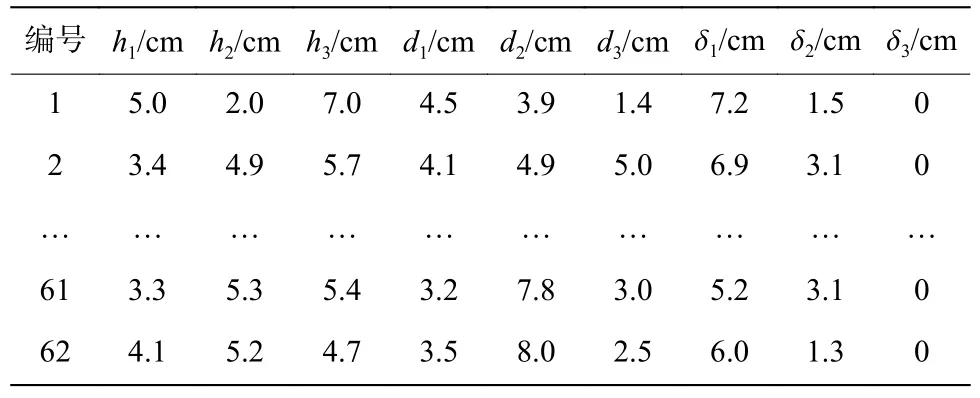
表4 数据集的输入值Table 4 Input values of the dataset

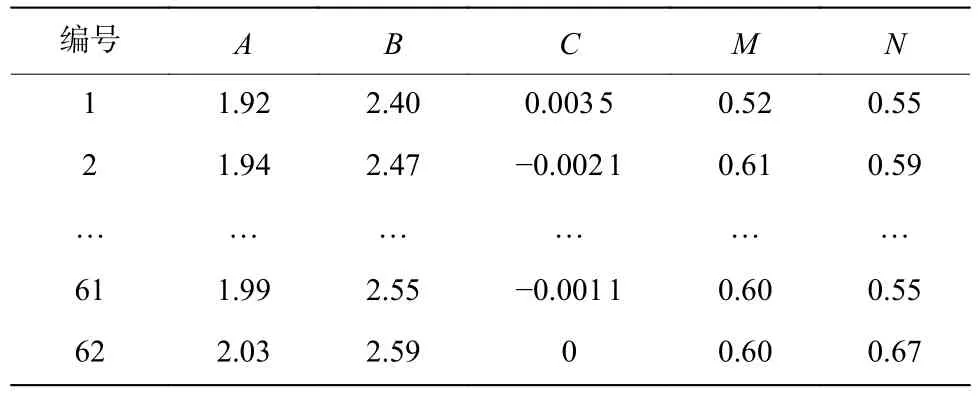
表5 数据集的输出值Table 5 Output values of the dataset

使用Python 语言建立神经网络模型，该模型由一个输入层、两个隐藏层和一个输出层组成，其中输入层有9 个神经元，输出层有5 个神经元，每个隐藏层有12 个神经元，如图5 所示。

图5 神经网络结构Fig. 5 Neural network structure

在训练模型过程中，将数据集的70%数据作为训练集，用来运行学习算法，30%作为测试集，将对算法的性能进行评估。神经网络模型的输入层与隐含层、隐含层与隐含层、隐含层与输出层之间的激活函数均采用ReLU 激活函数（linear rectification function）。选择测试集数据的预测输出值与实际输出值的绝对平均误差（mean absolute error）作为损失函数对由训练集数据训练出的神经网络模型进行优化。模型训练500 个迭代轮次（epochs），训练过程的损失函数随迭代轮次的增长变化如图6 所示，图中Loss 为训练集的损失值，Val_Loss 为测试集的损失值，可以看出该模型经过约200 次迭代训练后，Loss 与Val_Loss值统一下降，证明该神经网络的训练正常且目标函数收敛，因此可以根据此模型对PMMA 平板的JH-2 本构模型参数进行估计。

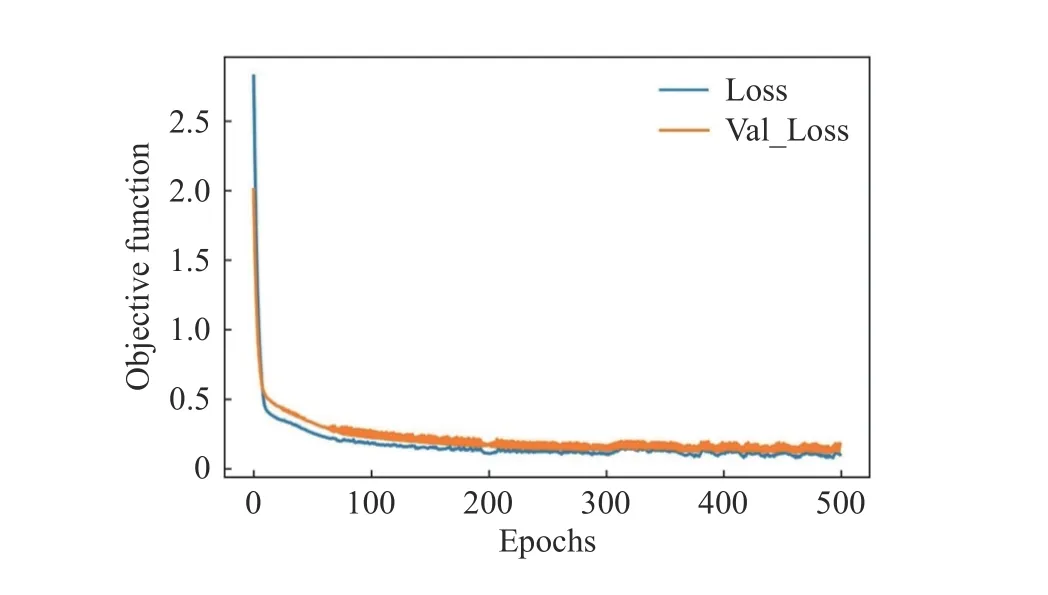
图6 目标函数收敛过程Fig. 6 Convergence process of the objective function

将2.3 节中的实验数据作为输入值输入神经网络模型，得到一套PMMA 平板的JH-2 本构模型参数，如表6 所示。

表6 PMMA 平板JH-2 本构模型参数反演值Table 6 Inversion values of parameters of PMMA flat plate JH-2 constitutive model

3 参数有效性验证

为验证本构模型参数反演值的有效性，本节首先使用反演出的参数对2.2 节中的试验进行数值模拟，模拟结果如图7 所示。

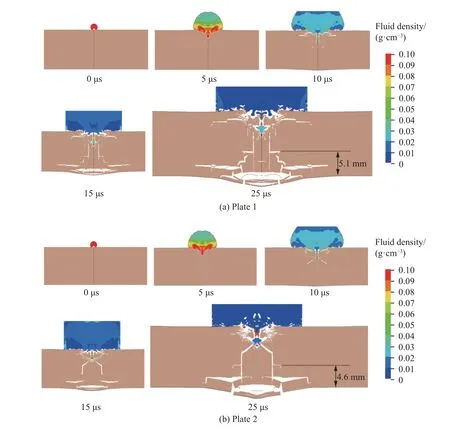
图7 PMMA 平板爆炸切割试验数值模拟结果Fig. 7 Numerical simulation results of PMMA flat plate explosive cutting test

对PMMA 平板爆炸切割数值模拟结果进行分析，从流体密度云图中可以明显看出爆炸切割索射流的形成、侵彻、减速和停止的整个过程，从而可以获得三种平板损伤中的侵彻深度。平板1 和平板2 下端在15 μs 时刻左右出现倒三角形状层裂，在25 μs 时刻损伤不再发展后可获得层裂厚度。表7 和图8给出了三种不同材质PMMA 平板爆炸切割试验结果和数值模拟结果的对比，可以看出数值模拟能够较为真实地复现出试验结果。

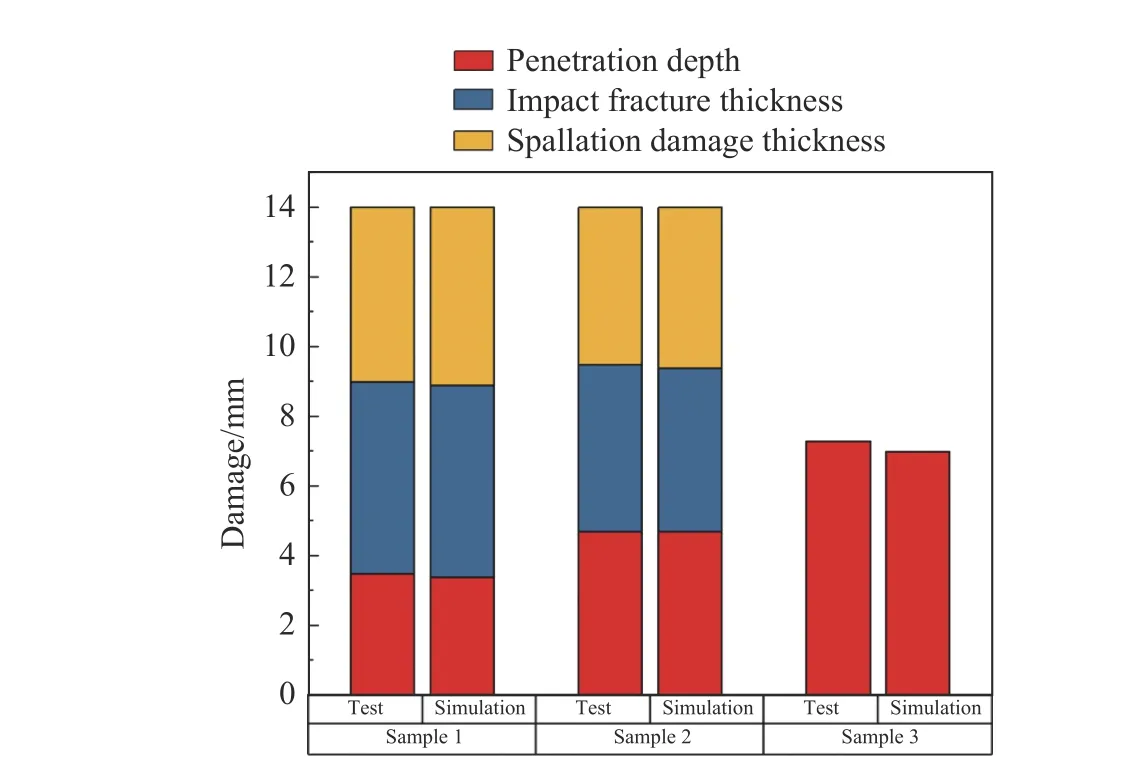
图8 试验结果与数值模拟结果对比Fig. 8 Comparison of test results and numerical simulation results

表7 试验结果与数值模拟结果对比Table 7 Comparison of test results and numerical simulation results

为了避免单一工况下反演参数验证的偶然性，进行一种不同工况下的PMMA 平板爆炸切割试验，并将试验结果与模拟结果进行对比。本节试验中PMMA 平板与平板3 为同种材质。

使用4.2 mm 宽的爆炸切割索对16 mm 厚、200 mm 宽的PMMA 平板进行爆炸切割试验。图9 为爆炸切割索横截面尺寸。可以从图10 展示的试验结果中明显看出PMMA 平板在爆炸切割下被切开，切口较整齐。切口中由射流侵彻的部分呈明显的黑灰色，即高速金属射流侵彻后所留下的残留物和痕迹。其余的断裂切口均为冲击形成的，并未出现呈倒三角形状的层裂损伤。经测量，侵彻深度约7 mm，冲击断裂厚度约为9 mm。

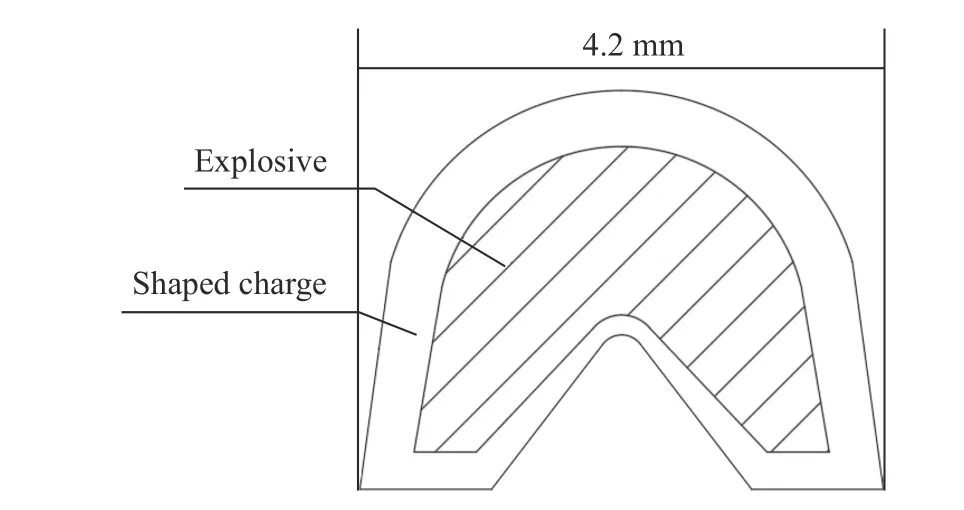
图9 爆炸切割索横截面Fig. 9 Cross-section of linear shaped charge

图10 爆炸切割试验结果Fig. 10 Explosive cutting test results

对该试验过程进行有限元数值模拟，模型尺寸如图9 所示，各部分材料参数采用2.2 和2.3 节中给出的参数。

图11 为有限元数值模拟结果。从图11(a)中可以明显看出爆炸切割索内的炸药爆炸后，其药形罩形成了金属射流，对PMMA 平板进行了侵彻，在15 μs 时刻左右，金属射流侵彻停止，侵彻深度为7.2 mm，在15～25 μs 过程中，PMMA 平板主要受炸药爆炸冲击波作用进一步损伤直至完全断裂，即冲击断裂厚度为8.8 mm。从图11(b)中可以看出应力波在PMMA 平板中的传播规律，应力波在8 μs 时刻到达PMMA 平板下平面，随后产生卸载波与入射波叠加产生拉应力。但在本工况中，应力波叠加产生的拉应力并不足以对PMMA 平板产生损伤，因此并未有层裂现象产生。可以看出反演参数的模拟结果与试验结果较为吻合，所建立的神经网络模型反演参数较为可靠。

4 总 结

(1) 根据有机玻璃（PMMA）平板爆炸切割试验的宏观实验数据反演PMMA 的本构模型参数是一种新的尝试。其相较于传统的本构模型参数获取方式优势在于只需要少量试验作为参考，即可获得相当准确的材料本构模型参数。

(2) 将神经网络智能算法应用于参数反演，建立起了基于神经网络的本构模型参数反演模型。为了反演的参数能够更好地反映工程中关注的PMMA 材料断裂模式和损伤状况，有针对性地将PMMA 平板损伤数据设置为神经网络的目标函数。验证结果表明，应用了反演参数的PMMA 本构模型在数值模拟中能够准确地模拟出材料的力学响应和损伤，即该反演模型所反演的材料本构模型参数能够达到较高的预测精度。