纤维素连续酶解反应器模型的研究

洪霞

（中石化上海工程有限公司，上海 200120）

糖是生产生物基化学品的重要原料，而纤维素酶解法制糖已成为研究热点[1]。目前酶解工艺普遍采用间歇操作，即在每一批原料酶解时均需要经过加料、酶解反应、出料和设备清洗等四个过程，存在操作流程长、设备利用率低、生产效率低等问题。连续酶解技术[2]可以解决现有技术中存在的问题，实现酶解的连续化操作，既可简化酶解操作过程，又可提高生产效率。开发纤维素连续酶解反应器成为实现酶解连续化操作的关键，但目前有关纤维素连续酶解反应器的基础理论研究较少。

本文根据酶解反应动力学和多级全混釜串联模型理论推导并建立了纤维素连续酶解反应器模型，并通过连续酶解实验对纤维素连续酶解反应器模型的参数进行求解，得到连续酶解得率x 和酶解停留时间t之间的纤维素连续反应器模型方程并验证了其准确性，为纤维素连续酶解反应器的开发和工程化放大奠定理论基础。

1 实验部分

1.1 实验原料

玉米秸秆预处理物料：采用螺杆蒸汽爆破预处理技术[3]对玉米秸秆原料进行处理，得到玉米秸秆预处理物料。对玉米秸秆预处理物料采用美国可再生能源实验室（NREL）方法[4]进行分析，得到玉米秸秆预处理物料的干物含量是35%，干物中纤维素含量是40%；酶制剂：采用商品酶（CTec3）；液碱：32%氢氧化钠溶液。

1.2 实验装置

实验采用纤维素连续酶解反应器，容积为1.5 L，如图1 所示。

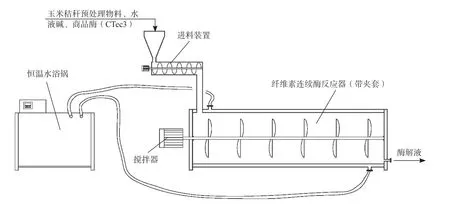
图1 纤维素连续酶解实验装置Fig.1 Cellulose continuous enzymatic hydrolysis experimental device

1.3 实验条件

纤维素连续酶解实验条件见表1。

表1 纤维素连续酶解实验条件Tab.1 Experimental conditions for continuous enzymatic hydrolysis of cellulose

1.4 实验方法

纤维素连续酶解的实验方法：开启进料装置和搅拌器，连续向纤维素连续酶解反应器中加入玉米秸秆预处理物料、水、商品酶（CTec3）、碱液，加料速率分别控制在12.6 g/h、9.1 g/h、0.09 g/h、0.3 g/h，控制底物浓度20%，控制物料pH 为5，物料在酶解反应器中的停留时间是72 小时，同时酶解液连续出料；开启恒温水浴锅，控制物料温度是50 ℃；当连续酶解实验稳定运行后，对纤维素连续酶解反应器出口的酶解液进行取样，并采用高效液相色谱（HPLC）分析测定酶解液中的葡萄糖浓度；取样工作完成后结束连续酶解实验。

2 结果与讨论

2.1 实验结果

纤维素酶解的化学反应方程式是[5]：

定义酶解得率为纤维素的转化率，其计算式如下：

其中，酶解底物浓度为20%。通过分析得到酶解液密度为1 100 g/L，玉米秸秆预处理物料干物中的纤维素含量为40%，酶解液中葡萄糖浓度为68.4 g/ L，由式（2）计算得到连续酶解得率为70.0%。

2.2 纤维素连续酶解反应器模型的建立

多级全混釜串联模型是一种常用的连续反应器模型，该模型是将连续反应器等效为由N个等容的理想全混流反应器串联而成[6]，如图2 所示。其中，N是一个虚拟的模型参数，用于表征连续反应器的返混程度，N与返混程度的对应关系如下：

图2 纤维素连续酶解反应器模型Fig.2 Model of continuous cellulose enzymolysis reactor

（1）当N为1 时，连续反应器内的物料返混程度为无穷大；

（2）当N为无穷大时，连续反应器内的物料返混程度为零。

对于纤维素连续酶解反应器模型，其模型参数N是介于1 和无穷大之间的一个数值。

图中C0——初始纤维素浓度，g/L；

Ci——第i个理想全混流反应器出口的纤维素浓度，g/L；

F——物料的流量，L/h；

N——连续酶解反应器模型参数；

ri——第i个理想全混流反应器的酶解反应速率，g/（L·h）；

V——每个等容的理想全混流反应器的有效容积，L；

x0——初始酶解得率，%；

xi——第i个理想全混流反应器出口的酶解得率，%；

x——连续酶解得率，%；

其中，i=1，2，……，N。

对模型中第i个理想全混流酶解反应器进行物料衡算，即：

纤维素进料量-纤维素出料量-纤维素反应消耗量=0

模型中的每一个全混流酶解反应器中物料的停留时间相同。

对第i个理想全混流酶解反应器，其停留时间ti为：

将式（4）代入式（3），得到：

根据化学反应动力学[7]，纤维素酶解化学反应速率ri可以表示为：

根据式（5）和式（6），得到：

由上式（7）可以得出：

按照酶解得率x的定义，可以得到：

将式（9）和（10）代入式（8），得到：

设连续酶解的停留时间为t，由于模型中的每一个全混流酶解反应器中物料的停留时间ti均相同，因此ti可表示为：

将式（12）代入式（11），得到连续酶解反应器模型是：

式中C0——纤维素初始浓度，g/L；

k——酶解反应速率常数，（g/L）-2·h-1；

n——酶解反应级数；

N——连续酶解反应器模型参数；

t——酶解停留时间，h；

xi——第i个全混流反应器所达到的酶解得率，%；

x——连续酶解得率，%。

2.3 纤维素连续酶解反应器模型的求解

2.3.1 纤维素初始浓度、酶解反应级数和酶解反应速率常数

纤维素连续酶解实验中，酶解干物浓度为20%，预处理物料纤维素含量为40%，酶解液密度为1 100 g/L，因此

纤维素初始浓度C0=酶解干物浓度×预处理物料纤维素含量×酶解液密度 = 20%×40%×1 100 g/ L=88 g/L

根据纤维素酶解反应动力学研究的相关报道[8]，得出以下结果：

（1）酶解反应级数n=3

（2）酶解反应速率常数k=2.13×10-5（g/L）-2·h-1

将以上结果代入纤维素连续酶解反应器模型，可以得到：

式中t——酶解停留时间，h；

N——连续酶解反应器模型参数；

xi——第i个全混流反应器所达到的酶解得率，%；

x——连续酶解得率，%。

2.3.2 纤维素连续酶解反应器模型参数N的求解

纤维素连续酶解反应器模型求解的关键是求出模型参数N，从而得到酶解停留时间t和酶解得率x的数学关系。

根据纤维素连续酶解实验条件，酶解停留时间t=72 h，代入式（15）可以得到：

通过采用试差法求解纤维素连续酶解模型参数N，即先假设一个模型参数N的数值，将N值代入纤维素连续酶解反应器模型计算得到酶解得率，将计算得到的酶解得率与连续酶解实验结果进行比较，直至模型计算结果与实验结果相符为止。

模型参数N的求解过程如下。

（1）根据酶解得率的定义，连续酶解初始时的酶解得率x0=0；

（2）假设N=1 时

纤维素连续酶解反应器模型是：

i=1 时，根据式（17）可以得到：

对x1求解得到：

由此可以得出：假设N=1 时，纤维素连续酶解反应器模型计算得到的酶解得率是62.5%。

（3）假设N=2 时

纤维素连续酶解反应器模型是：

i=1 时，根据式（17）可以得到：

对x1求解得到：

i=2 时，根据式（17）可以得到：

对x2求解得到：

由此可以得出：假设N=2 时，纤维素连续酶解反应器模型计算得到的酶解得率70.3%。

（4）同理可以得出：

假设N=3、N=4 和N=5 时，纤维素连续酶解反应器模型计算得到的酶解得率分别是73.3%、74.9%和75.8%。

（5）由以上结果可以得到模型参数N的数值与连续酶解得率计算结果之间的关系如表2 所示。

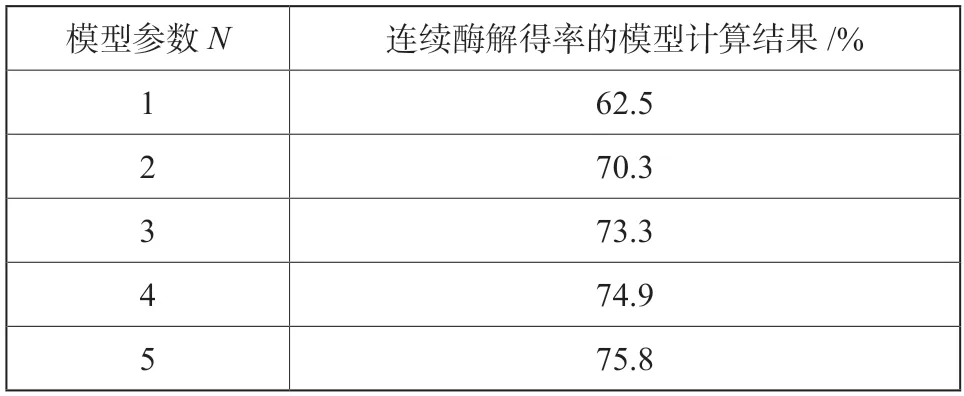
表2 模型参数N 的数值与连续酶解得率计算结果之间的关系Tab.2 Relationship between model parameter N and the calculated results of continuous enzymatic hydrolysis yield

（6）纤维素连续酶解实验结果为连续酶解得率70.0%。当N=2 时，连续酶解得率的模型计算结果是70.3%，此模型计算结果与实验结果基本一致。因此可以得出，模型参数N=2。

（7）将N=2 代入纤维素连续反应器模型方程中，得到：

由此可以得到：

连续酶解得率x=xN=x2，由此可以得到纤维素连续酶解反应器模型是：

式中t——酶解停留时间，h；

x——连续酶解得率，%。

2.4 纤维素连续酶解反应器模型的验证

假设酶解停留时间t=96 h，代入纤维素连续酶解反应器模型，求出连续酶解得率x=73.3%。

为了验证纤维素连续酶解反应器模型的准确性，开展了验证实验，实验条件见表3。

表3 连续酶解反应器模型验证实验条件Tab.3 Experimental conditions for model validation of continuous enzymolysis reactor

对以上验证实验得到的酶解液组分分析结果和连续酶解得率计算结果如表4 所示。

表4 酶解液组分分析和酶解得率结果Tab.4 Enzymatic hydrolysate component and enzymatic hydrolysis yield

即通过验证实验可以得出：酶解停留时间t=96 h 时，酶解得率为x=73.5%。

当酶解停留时间t=96 h 时，由纤维素连续酶解反应器模型计算得到的酶解得率为x=73.3%，通过验证实验得到的酶解得率为73.5%，两者误差仅为0.2%，由此验证了纤维素连续酶解反应器模型的准确性。

3 结论

根据纤维素酶解反应动力学和多级全混釜串联模型理论推导并建立了纤维素连续酶解反应器模型。采用螺杆蒸汽爆破预处理技术对玉米秸秆原料进行预处理，得到的玉米秸秆预处理物料作为实验原料，在20%底物浓度、5%（g/g 纤维素）商品酶（CTec3）加量、酶解停留时间72 h的条件下进行连续酶解实验。根据实验结果，对模型参数进行求解并得到酶解得率x和酶解停留时间t之间的纤维素连续酶解反应器模 型：

式中t——酶解停留时间，h；

x——连续酶解得率，%。

为对得到的纤维素连续酶解反应器模型进行验证，进行了96 h 的连续酶解验证实验。实验结果表明，纤维素连续酶解反应器模型的计算结果与实验结果基本一致，验证了纤维素连续酶解反应器模型的准确 性。