厘清逻辑 串联思维

李云珍

2021年7月，中办、国办联合印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》（以下简称《意见》），明确提到各地区应结合实际做好《意见》的执行落实。“双减”政策出现的目的就是为了减少学生的作业负担以及校外培训负担，使学生有更多的时间来参与体育锻炼，发展兴趣爱好等，可见国家对学生综合素养能力的提升是非常重视的。教师注重为学生减负的同时坚持育人，在数学课堂上树立全新理念，注重学生逻辑思维能力的锻炼与培养，使学生在学习知识的同时，又能够实现各项能力的全面发展，为数学知识的学习和应用奠定基础。

一、自主归纳，进行逻辑推理能力训练

逻辑思维能力可理解为学生第一时间发现问题相互间联系、实现问题解决的能力。而鼓励学生自主归纳的过程能够让学生对某个问题进行主动分析、独立思索，获得相互间联系，且在问题解决过程中获得知识，这与逻辑思维能力培养理念不谋而合。所以在小学数学教学中，教师应结合课本里所要讲解的内容计划性、目的性地引导学生进行知识点自主归纳，为培养逻辑思维能力提供条件。

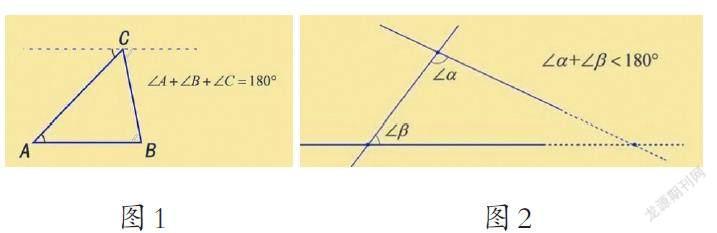
如在《认识三角形和四边形》里有这样一道题：证明图1中∠A+∠B+∠C=180°，即三角形的内角和为180°，那么可引导学生证明∠+∠<180°（如图2），虽然两种题型在内容上存在区别，但实际上其中的数学思想是一样的，也就让学生明白无论是什么样的三角形内角和均为180°，并对三角形的基本特征有更全面的了解，并弄清楚其中存在的关联性。

二、问题设置，进行逻辑推理能力培养

学起于思，而思源于疑。科学提问对于学生进行知识点的掌握与学习同样很重要，通过提问能让学生积极思索，大胆总结推理，达到发现问题与解决问题的目的。因此在小学高段数学课堂教学中，教师应结合教学内容进行问题的合理设置，来帮助学生明确各知识点之间的关系，促进逻辑思维能力不断提高。

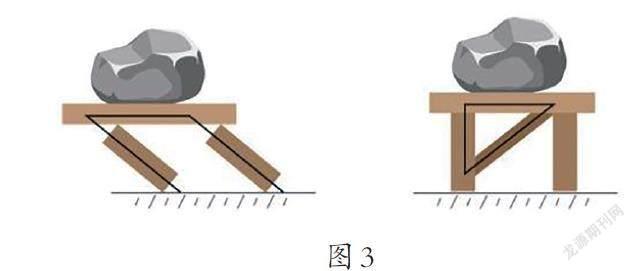
如在《认识三角形和四边形》相关知识学习中，同样可通过提问的方式让学生带着问题逐层思索与学习，即三角形、四边形的特征与性质。什么是三角形的内角和？三角形三个内角和是多少？为什么三角形具有稳定性？图3是什么原理？这样让学生带着问题去学习，边学习边思索，并通过动手实践等方式进行验证分析，可让学生发现与解决问题的能力、逻辑推理能力等核心素养得到提升。

三、举一反三，进行逻辑推理能力训练

举一反三同样属于强化学生逻辑推理能力的有效方法，因此需要为学生提供举一反三的机会，让学生依靠自主性的比较，明确知识点的联系与区别，促进逻辑思维能力培养。

小学数学知识学习中，“变式”教学方法为数学基础知识学习的可行举措，能够促使学生从不同条件、不同视角、不同结果进行数学习题的解答，实现不同知识点的融会贯通，进而强化学生对知识的理解，使学生探究和解决问题的能力得到提升。如在学习《百分数》相关知识点时，通过变式训练的形式提高学生的逻辑思维能力以及知识迁移能力，在这章节知识学习后可进行相关习题设置：某县今年计划造林20亩，实际造林18亩，实际造林是计划造林的百分之几？某县今年计划造林20亩，实际造林18亩，计划造林是实际造林的百分之几？某县今年计划造林20亩，实际造林18亩，实际造林是计划造林与实际造林总和的百分之几？这样举一反三的强化训练，对学生逻辑思维能力的培养也有一定好處。

四、情境创设，进行逻辑思维过程诱导

好玩是小学生的天性，小学数学课堂教学中教师应该根据学生性格、年龄等因素，依靠合理情境创设让学生出现认知冲突，确保学生思维始终处于积极学习状态，同时还能使学生在解决问题时慢慢从直觉思维状态向抽象思维状态转变，达到培养逻辑推理以及思维能力的作用。

如学习《圆的周长》时，需要进行圆周长公式的推导，由于圆形与学生先前所学的正方形、长方形等有差异，学生推导时思维极易受阻。若要让学生逻辑推理兴趣高涨，还应为学生创设这样的情境，即在一个圆内画出一个最大的正方形，并鼓励学生思索，若有两只小鸭在同一时间从圆形和正方形起点前行，哪只小鸭会提前到达终点，为什么？该情境融入了与学生年龄相符合的动物元素，所以学生的学习兴趣高，通过认真看图分析，能够发现一只小鸭所走的路程即是正方形的周长，而另一只小鸭所走的路程实质就是圆形的周长。若直径为d，那么正方形周长则为4d，后将圆的半圆铺平，发现半圆长度比正方形2d更长，这样就使学生通过推理轻松得出结论，达到培养逻辑思维能力的效果。

五、实践活动，进行逻辑思维能力拓展

《数学课程标准》把实践和综合运用纳进课本学习里，从而让学生数学应用意识与能力得到锻炼，促进综合素养全面提高。不过综合实践课内容可操作性相当强，应通过考查、分析、探究、操作等方式来领悟、感知与发现，且在该过程实现各项能力的提升。同时开展社会实践活动可确保学生的数学知识学习从课堂走向社会，达到课本知识与现实生活的有机融合，确保体验式学习模式得到实现，进而提升逻辑思维能力。

在“圆”的概念相关知识教学时，应根据教材内容引导学生通过小组方式在学校里或家庭中发现形状是圆形的物体，或在学校篮球场或足球场内画出若干个圆形与半圆形，鼓励学生自己动脑，并使用工具进行周长测量；或发给学生长度相同的绳子，鼓励学生利用绳子依次围作圆形并思考如何计算出所围出圆形的周长与面积，这一动手操作实践的过程也是学生思维锻炼的过程，让学生学到书本里没有的知识。

六、数形结合，进行逻辑推理能力挖掘

数形结合思想即借助几何图形的性质来表达一些抽象的数量关系或数量概念，使课本中涉及的数学知识与概念能够更加形象直观地为学生进行展示，帮助学生进行知识点的消化理解，或把复杂的数学图形问题转化成简单的数量关系，助力学生得到更准确的结论，使学生轻松地掌握数学知识要点。数形结合思想属于整个数学教学过程中十分重要的思想，通过掌握数形结合思想，能够帮助学生更好地掌握数学知识，可以将抽象数学问题变得具体化，把复杂问题变得简单化，使得抽象思维转变为形象思想，促进学生轻松掌握数学问题的本质。因此，教师在日常教学中应有意识、有目的地引导学生利用数形结合思想解决复杂的数学问题，帮助学生理清解题思路的同时，又达到促进学生逻辑思维发展的效果，为其后续数学知识学习奠定基础。

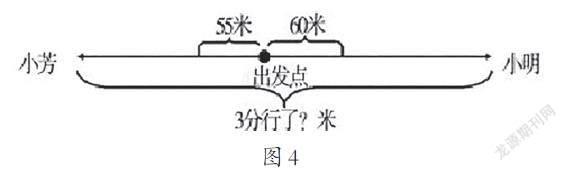
如这样一道应用题：学生小明与学生小芳同时从相同位置出发，小明以每60米/分钟的速度向东边行走，但小芳以55米/分钟的速度向西边行走，问3分钟后，两人间距多少米？针对题目里的隐形条件，如果不通过图形的方式帮助学生进行理解分析，要得出最终的答案有一定难度。但是如果学生能够结合已知条件，进行图形绘制，并挖掘思维突破口（见图4所示），就能够明确地看出究竟是要求哪里到哪里的距离，这样让整个题型显得更加直观易解，理清题目中蕴含的逻辑关系，并得出最终结果。

小学数学教学务必要积极顺应政策要求，充分掌握政策的优越性以及前瞻性，正确认识政策倡导的减负意义，主动进行教学模式调整，在展开多元化课外作业设置的同时，不断强化学生逻辑思维能力培养，让数学课堂变得轻松有效。

（焦  佳  左毓红）