多个经验模态分解对振动信号作用的对比

赵楠 石振刚

摘要：经振动传感器采集到的信号是非线性、非稳定的，这种信号无论是在时域还是频域上都不易分析。所以通过经验模态分解将原始信号分解成为多个本质模态函数（IMF），之后对其进行特征提取等进一步处理。但是经验模态分解存在模态混叠与端点效应的问题，所以文章采用互补集合经验模态分解（CEEMD），CEEMD是在進行经验模态分解之前加入多组符号相反的白噪声，这不仅减少了模态混叠，分解出的IMF分量还更精进。这种互补集合经验模态分解有效地处理了所采集的非线性，非稳定性的振动信号。

关键词：振动信号  经验模态分解  本质模态函数  互补集合经验模态分解

中图分类号：TN911        文献标志码：A

Comparison of the Effects of Multiple Empirical Mode Decomposition on Vibration Signals

ZHAO Nan  SHI Zhengang*

（School of Information Science and Engineering， Shenyang Ligong University， Shenyang， Liaoning Province， 110158 China）

Abstract：The signal collected by vibration sensors is nonlinear and unstable， and this kind of signal is difficult to analyze in either time domain or frequency domain. Therefore， the original signal is decomposed into multiple IMFs through empirical mode decomposition and then is further carried out processing such as feature extraction. However， modal aliasing and endpoint effects exist in empirical mode decomposition， so this paper adopts CEEMD. CEEMD is to add multiple groups of white noises with opposite signs before empirical mode decomposition， which not only reduces mode aliasing， but also makes the decomposed IMF component more refined. The complementary ensemble empirical mode decomposition effectively deals with the collected nonlinear and unstable vibration signals.

Key  Words： Vibration signal; Empirical mode decomposition; Intrinsic mode function; Complementary ensemble empirical mode decomposition

经振动传感器采集得到的振动信号，是一个非线性、非平稳的信号。通常于信号的时域或频域上对信号进行分析与特征提取。而振动信号在时域上无法观测出信号的特征，在频域上，能看出是多个信号进行了叠加，这对于信号的分析，造成了干扰。经验模态分解（EMD）是一种适用于非线性非平稳信号的时频分析方法。

王若平[1]等人采用了一种用EMD改进Mel倒谱系数的方法，来对低信噪比的交通环境进行特征提取。该方法在一定程度上提高了特征参数的抗噪性，同时提高了后续的识别率。邹瑛珂，贾云飞[2]等人在改进EMD基础上，对野外的人和车振动信号进行识别。对改进之后的经验模态分解分解出的IMF分量进行特征提取，提高了后续的分类器分类的准确率。曾成[3]也在地震信号研究中，运用到了CEEMD方法。张恒[4]在研究无人值守这一课题中，提到EMD可以自适应对振动信号进行分解，且有较高的准确率。CEEMD也被经常应用于轴承故障的识别，NIU D P、WANG J Q[5]、汪一飞[6]用CEEMD来判断滚动轴承的故障，涉及到的信号为振动信号，这种方法能准确判断出故障原因及位置。孟繁雯[7]在研究矿井主通风机轴承时，也将EMD与CEEMD进行对比，发现CEEMD分解效果优于EMD。

经验模态分具有自适应性，无需预先对信号进行分析，就会将信号分解成为多个本质模态函数（IMF）。但是经验模态分解有两个缺点，一个是模态混叠，另一个是端点效应。这两个缺点一个会影响信号的特征提取，另一个会造成信号两端的包络严重扭曲，使信号信息遭受损害，影响判断。为了解决模态混叠，在信号进行分解前加入随机的白噪声，也就是EMD的衍生方法集合经验模态分解（EEMD）。但是添加的白噪声存在个体差异，在下一步进行经验模态分解时，会造成新的混叠，同时可能会有无法消除的信号累积在原始信号中，影响信号的分析及特征提取，在对IMF分量成分进行集合平均时，还会造成运算时间的增加。所以本次实验使用互补集合经验模态分解（CEEMD）。互补集合经验模态与集合经验模态的区别在于互补集合经验模态分解加入的白噪声是一对互为相反数的正负白噪声，可有效地降低了运算律与消除信号重构后的残余辅助白噪声。

1 经验模态分解

经验模态分解的原理是通过寻找信号的极大值点雨帘云栋极小值点，分别形成上、下两个将极值点都包含在内的包络，然后取两个包络间的平均值，用原始信号减去平均值，得到一个新的信号，对此信号重复上诉步骤，直到满足IMF的条件，即可得到一个IMF分量，具体运算过程如下。

（1）通過三次样条函数拟合出极大值包络线，以及极小值包络线。

（2）计算上、下包络的平均值。

（3）构造一个新信号，该信号是原始信号去掉了一个低频信号。

但此时得到的信号并不是稳定的，所以继续重复上述步骤，直到满足IMF的定义为止，才算是找到原信号的一阶IMF分量。

用原始信号减去上述得到的IMF分量，得到了一新的去掉高频成分的信号。

重复上述步骤，直到EMD停止分解。满足n阶的IMF分量或残余分量小于预设值，或者残余分量为单调函数或者常量二者条件之一即可。

（4）原信号与IMF分量和残余分量的关系如下。

本质模态函数（IMF）有两个约束条件，一个是在整个数据段内，极值点的个数和过零点的个数必须相等或相差最多不能超过一个。另一个条件是在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零，即上、下包络线相对于时间轴局部对称。

2 互补集合经验模态分解

为了缓解经验模态分解的混叠问题，法国的EMD算法研究小组与Huang共同研究发现在原始信号中加入白噪声，使得原始信号的缺失的时间尺度被填补，也就是EEMD。但是由于造成新的混叠以及运算时间的增加，提出了新的运算方法—互补集合经验模态分解（CEEMD）。CEEMD中所加入的白噪声数值一致，但符号相反，这种方法消除了白噪声在原始信号中的累积。CEEMD的算法过程如下。

（1）在原始信号进行经验模态分解之前，先添加多组符号相反的白噪声。

（2）对所添加了白噪声的信号进行经验模态分解处理，将得到的多个IMF分量，分别进行平均集合。

（3）将所得的正负平均集合再次进行平均集合，即得到总体平均的IMF分量。

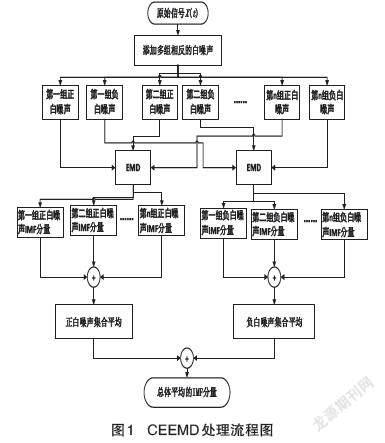
经过互补集合经验模态分解的信号的IMF，要比经验模态分解得更加准确，大大的减少了模态混叠，CEEMD的流程图如图1所示。

3 振动信号仿真

实验的数据有两种，一种是人体脚步的振动信号，另一种是车辆行驶的振动信号。首先，振动传感器采集数据以后，将数据封装在txt文件中，通过Numpy函数中的loadtxt语句对数据文件进行调用读取。之后，在对数据进行模态分解之前，用pywt小波函数，对原始信号进行去噪，将去噪之后的信号再进行模态分解。最后，引用PyEMD函数，对去噪之后的函数分别进行经验模态分解、集合经验模态分解与互补集合经验模态分解。使用matplotlib函数绘画原始信号图、去噪信号图、各个经验模态分解之后的IMF分量图，直观观测哪个算法更适合处理本实验数据。

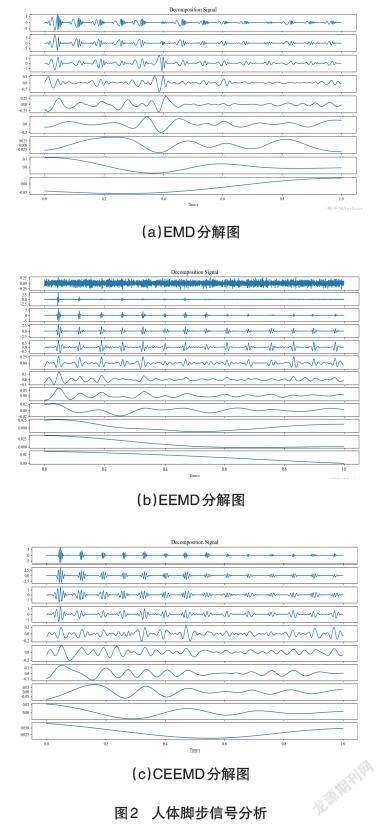
根据图2所示，图2（a）为经验模态分解图，图2（b）为集合经验模态分解图，图2（c）为互补集合经验模态分解图。对比图中这3种分解的前几个IMF分量，能明显看出CEEMD的分解结果要更精准，EMD与EEMD的模态混叠现象要严重。对比这3种分解的后几个低频IMF分量，无明显区别，但是可以看出EMD和CEEMD的IMF数量要少，从而证明了EMD和CEEMD的运算次数要少，也就是程序的运算速度高一些。

综上所述，CEEMD算法在人体脚步信号分析中要好一些。

图3是车辆行驶信号的仿真结果图，图3（a）为经验模态分解图，图中能明显看出IMF的分解数量较少，说明信号的有用信息未被准确分解出来，这可能会造成实验结果的误差，因此实验中不考虑EMD。

图3（b）为集合经验模态分解图，图3（c）为互补集合经验模态分解图。观看这两幅图的IMF分量，可以看出EEMD的前3个IMF分量与原始信号无太多的分别，在进行IMF分量重构时，不仅没有优势，反而对实验分析造成了困扰。而CEEMD则不存在这个问题，而且CEEMD中的低频IMF分量要少于EEMD，减少了后续分量重构的次数，更具完备性。

综上所述，CEEMD无论是在人体脚步信号分解中还是在汽车行驶信号分解中都具有优势，所以本次实验中会采用CEEMD。

4 结语

经验模态分解是将非平稳、非线性的信号分解成为多个IMF分量，所分解成的IMF分量，具有原始信号的信息。为了进行下一步的特征提取，可以将其中的IMF分量自行重构，并进行分析，也可以逐个对IMF分量进行分析。研究中，对人体脚步和汽车行驶信号分别进行了经验模态分解、集合经验模态分解、互补集合经验模态分解，无论是从IMF的高频分量还是低频分量上，互补集合经验模态分解的效果都是最好的。

参考文献

王若平，李仁仁，陈达亮，等.基于改进小波包去噪与梅尔倒谱系数的低信噪比交通环境声音识别[J].科学技术与工程，2019，19（36）：290-295.

邹瑛珂，贾云飞，刘素芸.一种基于改进EMD分解人车地震动信号识别算法[J].中国测试，2022，48（4）：85-94.

曾成.基于改进阈值函数与CEEMD的地震信号去噪算法[J].长江信息通信，2022，35（6）：75-77.

张恒.地面传感器智能监测系统及目标分类算法研究[D].长沙：国防科技大学，2019.

NIU D P， WANG J Q. Elevator Car Vibration Signal Denoising Method Based on CEEMD and Bilateral Filtering[J].Sensors，2022，22（17）：6602.

汪一飞.基于全矢CEEMD的滚动轴承故障诊断研究[D].郑州：郑州大学，2019.

孟繁雯，谢子殿，韩龙.矿井主通风机电机轴承振动信号EMD和CEEMD故障提取对比研究[J].科学技术创新，2022（1）：137-140.