基于环境历程的固体火箭发动机贮存可靠性计算方法①
鞠宏艳,贾东明,秦鹏举,李 毅,王思彤
(1.中国航天科技集团有限公司四院四十一所,西安 710025;2.西北工业大学 燃烧、热结构与内流场重点实验室,西安 710072)
0 引言
固体火箭发动机(以下简称发动机)是一次性使用的产品,作为各种导弹、运载火箭和航天器的主要推进装置,贮存可靠性对使用任务的完成起着至关重要的作用[1]。可靠性要求是贯穿整个贮存期的,长期贮存后的发动机可靠性会逐步下降。因此,贮存期内必须要保证发动机的可靠性满足使用要求。
发动机的初始可靠性因为在出厂时有大量的生产、试验数据可用,可以比较容易确定,而长期贮存以后的发动机,其材料性能、结构形态已经发生了变化,出厂时的数据已经不足以支撑评估此时的产品状态。因此,确定发动机的贮存可靠性是在没有充分数据的基础上进行的,其理论研究会比初始可靠性的理论研究更加困难。
目前,国内外针对发动机贮存的研究多数是从研究推进剂老化机理入手,基于药柱长时间贮存进行的加速老化试验获取推进剂伸长率变化规律,以及通过有限元计算等方法[2-7],对药柱的贮存可靠度进行预计,也有文献提出了综合网络模型与加速老化、结构完整性计算的装药贮存寿命预估模型,来预测贮存寿命[8]。但所有这些研究都是针对发动机局部材料或结构的贮存寿命及规律,没有对发动机贮存过程全系统可靠性计算方法的研究。
在研究推进剂老化和贮存规律的基础上,本文针对发动机常用非金属材料贮存的常用模型,从材料层次首次研究了各部组件在经历多种环境历程后的可靠性计算方法,并通过整机可靠性模型计算出发动机的可靠性,从而提出了适合发动机贮存可靠性计算的通用方法。
1 发动机整机可靠性模型的建立
根据相关标准,发动机的整机可靠性模型是发动机的I、II类故障模式作为可靠性单元的串联模型[9],即先根据FMEA的结果确定发动机所有的I、II类故障模式,然后将每个故障模式看作是一个可靠性单元,将发动机看作是这些可靠性单元的串联系统,发动机的可靠度R等于各个可靠性单元可靠度的乘积[10],即
(1)
式中Ai为某个故障模式;P(Ai)为故障发生的概率。
根据对许多型号发动机长期贮存后数据统计分析结果,从性能和结构两个方面看,发动机性能如平均压强、工作时间、比冲等指标的变化不显著,但有部分发动机的结构长期贮存后会发生变化。例如,药柱力学性能下降、界面粘接性能下降等。因此,贮存主要影响发动机的结构的可靠性。
在贮存期间发动机所有的I、II类故障模式本身不会发生变化,变化的只是其发生概率。因此,有
(2)
式中H为某环境;t为产品在H为环境下的经历时间;R(H,t)即H环境中贮存t时间的发动机可靠度。
一般情况下,发动机老化故障中Ai的故障判据为应力>强度,此为故障发生的应力强度模型,即有故障发生概率:
(3)
式中Q为强度;Y为应力;σQ和σY分别为强度和应力的标准差;Φ(.)为正态分布函数。
根据目前发动机贮存研究的成果,发动机在长期贮存后工作过程中其燃气温度和压强都不会发生明显的变化,可以认为燃气各参数分布规律与刚出厂时相同,因而来源于燃气的应力或强度不随着贮存时间变化,其概率分布与初始可靠性时的概率分布相同。
如果应力或强度来源于材料自身的性能,如粘接强度、伸长率等,这些性能将随着环境和贮存时间而发生变化。
不失一般性,可以认为强度Q来源于材料自身的性能,而其应力Y来源于发动机工作过程中的燃气,方差不随时间的变化而变化。因此,有
(4)
式中K(H,t)=Q/Y为安全系数;K0=K(H,0)=Q0/Y为初始安全系数;Q0为材料初始强度;ηQ=σY/Y为强度变异系数;ηY=σr/Y为应力变异系数。
2 影响材料贮存可靠性的环境定义
材料的实际贮存环境千差万别,为简化研究,本文提出一种新的研究思路:先指定一个标准环境,实际环境看作是标准环境+差异性,这样可以将标准环境的贮存数据作成手册,无需各单位重复进行研究,差异性则根据具体差异通过修正系数修正到实际环境数据。
材料标准环境包括标准贮存环境和标准测量环境两种,这里贮存环境指材料在测量其性能前的历史历程中的环境,而测量环境是指对材料进行性能测量时的环境条件。
材料的标准贮存环境在本文定义是指环境温度为20 ℃,相对湿度≤30%,一个标准大气压,无机械外力,无振动,无冲击,无辐射,无日晒,噪声≤80 dB,重力加速度为1g,无静电的环境条件。用字母HB表示该标准环境。
材料的标准测量环境与要求的测量项目有关,一般要求与标准贮存环境尽可能一致。例如,对非金属材料拉伸性能测量,标准测量环境定义为标准试件受到拉应力作用,拉伸速率为100 mm/min,其余要求同材料的标准贮存环境。
材料的实际贮存环境通常是标准贮存环境有部分参数改变而来。例如,温度环境有别于标准贮存环境、力学环境有别于标准贮存环境等,这些环境统称为非标准环境。
发动机实际贮存过程中所经历的非标准环境条件[10]有以下一些类型:
(1)第1类非标准环境:只有温度不满足标准环境要求。
如果发动机放置在密封容器如密封的发射筒中,且密封容器中的环境除温度外始终不变,则发动机除推进剂外所有材料均符合该非标准环境;如果发动机放置在与大气相连通的环境中,但发动机燃烧室处于密封状态,则燃烧室中除推进剂外所有材料符合该非标准环境;所有的小型火工品符合该非标准环境。这种环境条件只考虑温度的影响。
(2)第2类非标准环境:温度和应力不满足标准环境要求。
在发动机设计方案中,如果燃烧室是密封的,则药柱符合该类非标准环境。
药柱内部受力大小受到温度和应力的双重影响,但应力的大小与部位有关,还与温度有关。一般情况下药柱故障都发生在药柱表面和药柱与绝热层、人工脱粘层等的粘接面上,根据药柱结构完整性分析结果,这些部位药柱贮存中的主要受力情况如下:
1)药柱受到两向应力的作用。药柱局部只受到第一主应力和第二主应力的作用,这种情况主要发生在药柱表面。此时在弹性模型的计算中,第二主应力与第一主应力的比值是个常数,即与温度无关。
2)药柱受到两向应力和恒定剪应力的作用。当贴壁浇注的药柱处于竖起的状态时,药柱与绝热层的粘接界面处就符合该受力,此时剪应力为恒定值,第二主应力与第一主应力的比值是个常数。
3)药柱受到两向应力和恒定比例剪应力的作用。药柱与自由装填药柱包覆层粘接面、药柱与人工脱粘层粘接面处符合该应力,此时第二主应力与第一主应力的比值是个常数,剪应力与第一主应力的比值也是一个常数。
4)药柱受到复杂应力的作用。药柱在人工脱粘层的根部的受力为复杂应力,药柱为三向受力以及剪切应力均有的状态,但是在弹性模型中,各向受力的比例与温度无关。
根据上述情况分析,药柱内关键部位的受力程度都可以用Von Misses应力的大小来表征。因此,药柱表面及粘接面上Von Misses应力最大的部位就是最危险的部位。
(3)第3类非标准环境:振动不满足标准环境要求。
当两个部组件之间存在着相互摩擦时会遇到这类非标准环境,例如人工脱粘层、紧固件适用于这类非标准环境。
(4)第4类非标准环境:发动机表面环境不满足标准环境要求,包括湿度、气压、微生物、盐雾、粉尘、日晒、雨淋、结冰、冰雹、雪、空气污染、温度交变等。
这类非标准环境作用于发动机表面,针对这类环境需要在发动机表面(包括壳体外表面、喷管外表面、喷管扩张段内表面等部位)采用喷漆等防护措施,在设计阶段,需要调查发动机表面涉及的各种材料的应用情况,据此来分析各材料的环境适应性,如果各材料的环境适应性不能满足要求,则不能用于相应产品。
3 单元贮存可靠性计算方法
3.1 标准贮存环境下的材料贮存可靠性
材料在标准贮存环境下经历了t时间,材料的某个敏感参数会发生较大变化,该敏感参数是一个随时间变化的变量,即有
Q=Q(HB,t)
(5)
在QJ 2328A—2005《复合固体推进剂高温加速老化试验方法》中提供了三种标准的材料敏感参数变化曲线[11]:
标准强度曲线1:
Q(t)=Q0exp(-Zt)
(6)
标准强度曲线2:
Q(t)=Q0(1-Zt)
(7)
标准强度曲线3:
Q(t)=Q0(1-Zlnt)
(8)
也可以统一地表述为
Q(t)=Q0f(Z,t)
(9)
式中Z为老化参数;Q为材料的某个贮存敏感参数,如伸长率、抗拉强度等。
标准贮存环境下的老化参数设为ZHB。
上述模型虽然是复合固体推进剂的标准中提出的,但也适用于发动机常用其他非金属材料,特别是式(9)的适用范围很广泛。
为了确定Z参数,通常采用额定寿命τ进行测量,这里定义τ是指材料的性能下降到其初始值的70%时所需的时间,即满足Q(τ)=0.7Q0,可根据对应的曲线模型计算出Z参数。
在标准贮存环境下,可以根据实际统计数据确定材料的额定寿命τHB,也可以采用热加速老化试验的方法测定额定寿命τHB。τHB是材料的基本参数,研究产品的寿命首先需要测定该参数。可根据F(ZHB,τHB)进一步计算出ZHB。
对于给定的贮存期t,对应的单元贮存可靠性为
Ri(HB,t)=1-P(Ai|HB,t)
(10)
3.2 恒定非标准贮存环境下的材料贮存可靠性
在恒定的非标准环境下,其基本思路与标准环境下解决问题的思路一致,也是通过额定寿命τ来确定参数Z,并进而确定对应的贮存可靠性,只是确定额定寿命τ时,需要统计的是指定的非标准环境下的非标准额定寿命τH,并根据f(ZH,τH)=0.7进一步计算出ZH。
对于标准强度曲线1,有
(11)
对于标准强度曲线2,有
(12)
对于标准强度曲线3,有
(13)
定义环境因子:
(14)
则对于标准强度曲线1和2,有
(15)
对于标准强度曲线3,有
(16)
同标准贮存环境的情形,对于给定的贮存期t,对应的单元贮存可靠度为
(17)
3.3 多阶段贮存历程下的材料贮存可靠性
材料经历了m个贮存历程,设第j个贮存历程里环境为Hj,持续时间为Δtj,需要计算在此历程后的单元贮存可靠性。
在第j个贮存历程中,设开始时的材料强度为Qj-1,本历程结束后材料强度为Qj,其中Qj-1是已知的,而Qj需要求解,求解的一般方法如下:
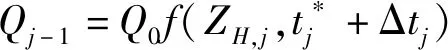
(18)
最终求出Qm,单元贮存可靠性为
(19)
特殊地,对于符合标准强度曲线1的强度模型,有
(20)
(21)
对于符合标准强度曲线2的强度模型,有
(22)
(23)

3.4 已知初始可靠性时的材料贮存可靠性计算方法
在很多场合,很难确定变异系数ηQ和ηY,却比较容易通过试验确定产品的初始可靠性:
(24)
此时,有
(25)
4 非标准环境下单元贮存可靠性计算方法
4.1 第1类非标准环境单元贮存可靠性计算方法
这类非标准环境只有温度与标准环境有差异,设温度的影响符合阿伦尼乌斯公式[12],即有
(26)
其中,E为材料的活化能;R=8.314 J/(mol·K)为气体常数;T为环境温度;T0=293.15 K为标准环境的温度。
此时的环境因子:
(27)
特殊地,对于符合标准强度曲线1的强度模型,有
(28)
对于符合标准强度曲线2的强度模型,有
(29)
4.2 第2类非标准环境单元贮存可靠性计算方法
此时温度对材料的强度有影响,同时应力也会对材料的强度有影响,导致材料某个敏感参数发生较大变化。一般情况下需要通过试验测量函数关系式τ(T,σ)=τHB/g(T,σ),环境因子C(T,σ)=g(T,σ),据此可计算出任意历程下单元贮存可靠性,其中T为温度,σ为应力,一般采用Von Misses应力。
由于在多数情况下温度和应力的影响是互相独立的,此时采用的环境因子为
(30)
此时,只要测定g(σ)即可。计算贮存可靠性可参考3.3节“多阶段贮存历程下的材料贮存可靠性”的计算方法。
4.3 第3类非标准环境单元贮存可靠性计算方法
这类非标准环境与其他非标准环境不同的是,紧固件涉及到至少两个部组件的对接,也就是至少涉及两种材料。因此,无法归结为某种材料的贮存可靠性问题。
目前常见的做法如下:对紧固件如果采取有铅封、涂胶等防松动措施则认为贮存可靠性为1,如果没有采用防松措施,以功率谱密度作为反映振动程度的变量时,并认为在恒定功率谱密度的振动环境作用下坚固件的松动服从指数分布,可以通过指定功率谱密度W0的振动环境下所进行的定数截尾试验或定时截尾试验来测定此时的MTBF(W0),则在任意功率谱密度W振动环境下的MTBF(W)为
(31)
其中,λ=2.5~4,如果没有确切数据,可选择λ=2.5。
对于振动环境历程(W1,Δt1),(W2,Δt2),…,(Wm,Δtm),期间紧固件不发生松动的可靠性为
(32)
4.4 第4类非标准环境单元贮存可靠性计算方法
这类材料由于处于发动机的外表面,比较容易观察到其缺陷,同时其故障模式的后果严重度不高,一般在设计阶段不考虑其贮存可靠性,而采用现场统计的方法进行持续改进,对已交付的产品采用维修的手段予以解决。
5 某发动机的贮存可靠性计算
基于本文建立的贮存可靠性的计算方法选取某发动机贮存老化试验结果进行分析。
示例:某固体火箭发动机所经历的历程为总装1 a,库房条件,温度(20±5)℃;库房贮存8.5 a,温度(22±2)℃;战备值班根据值班时间最长的发射车上温度统计结果见表1。

表1 值班时间和温度Table 1 Duty hours and temperatures
现在计算经历了上述历程后药柱的可靠性。
根据第3章和第4章中的公式,直接将已知的参数带入公式,并进行计算。
在研制期间,测得该发动机的推进剂的寿命敏感参数是抗拉强度σm,数据符合式(6),其方程为
(33)
式中σm(t)为推进剂抗拉强度,MPa;σm(0)为推进剂抗拉强度初始值,MPa;T为贮存时温度,K;t为贮存时间,d。
由此分析,该推进剂额定寿命(单位:d):
(34)
活化能E=4856.68×R=40.4 kJ/mol,其中气体常数R=8.314 J/(mol·K)。根据产品的活化能和气体常数,式(33)、式(34)可以进一步改写为
(35)
其中,T0=293.15 K。
根据应力/应变-寿命试验结果,测得在常温恒定拉应力σ下推进剂抗拉强度σm下降到70%时的时间τ(σ)满足方程
(36)
因此,将τ(σ)代入式(35),可得恒定拉应力σ以及温度联合作用下推进剂抗拉强度σm:
ln(σm(t))=ln(σm(0))+ln0.7×
=ln(σm(0))+ln0.7×
其中
根据线弹性模型计算本产品的药柱结构完整性,得到药柱最大Von Misses应力与温度的关系式:
σ=0.091-0.00107(T-283.15)
根据4.2节环境因子的公式,即
(37)
计算得到不同温度下药柱的环境因子见表2。
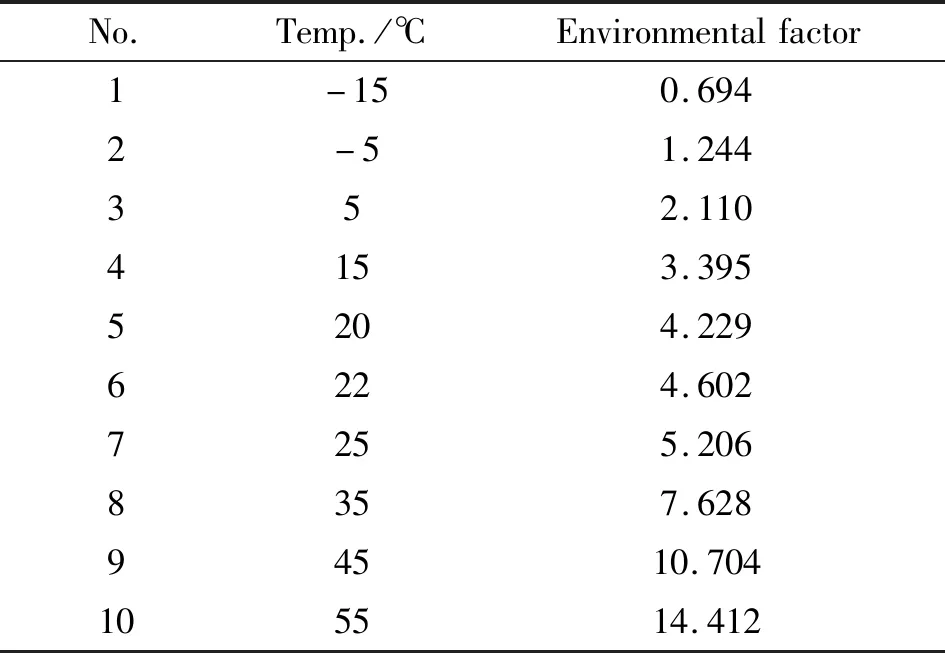
表2 药柱不同温度下的环境因子计算结果Table 2 Calculation results of environmental factors at different temperatures of grain
由式(20),根据给定的库房及值班环境历程,先计算等效标准环境条件推进剂的贮存时间(单位:d)为
t*=1×365.25×4.229+8.5×365.25×4.602+
(13×0.694+186×1.244+1503×2.110+
1887×3.395+3107×5.206+3437×7.628+833×
10.704+18×14.412)/24=77218.55
因此,推进剂强度为
σM(t*)=0.777218.55/45496.83σm(0)=0.546σm(0)
接下来计算密封圈的可靠度,根据对固体火箭发动机硅橡胶密封圈贮存寿命的研究得到密封圈老化反应速率K的Arrhenius 模型[13]:
K=381exp(-3083.3/T)
(38)
根据公式计算得到20℃下,K0=0.010306。
密封圈的寿命以压缩永久变形率为性能表征参数,压缩老化性能=1-压缩永久变形率。
压缩老化性能公式:
f(P)=exp(-Kt0.4)
(39)
通过公式可以看出,密封圈初始压缩老化性能即t=0时,f(P0)=1,即压缩永久变形率为0。
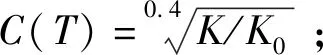

表3 密封圈不同温度下的环境因子计算结果Table 3 Calculation results of environmental factors at different temperatures of sealing ring
根据给定的环境历程,等效标准环境条件密封圈的贮存时间(单位:d)为
t*=1×365.25×1+8.5×365.25×1.028919+
(13×0.565298+186×0.675544+1503×
0.797016+1887×0.929599+3107×1.073102+
3437×1.227271+833×1.391794+18×
1.566316)/24=4052.36
因此,密封圈贮存后的老化性能:
f(P)=exp(-0.010306×4052.360.4)=0.751
设计定型时,密封圈安全系数为3,初始可靠度R=0.999999,则经历了给定的环境历程后该密封圈的可靠度为
除了药柱和密封圈,可以用同样的方法求出发动机其余材料和单元的可靠度,再根据发动机实际的串并联模型算出发动机的可靠度。
6 结论
本文从材料层次研究了发动机各部组件贮存可靠性规律,得到贮存可靠性与发动机环境历程的关系,为简化研究难度,定义了标准环境并给出分析,各材料标准环境下的贮存参数可以作为确定部组件寿命的基础数据,在此基础上通过修正系数来确定实际环境的贮存参数。本文将发动机的非标准环境分为四类,给出了不同环境修正系数的计算方法,并进一步给出了多种环境历程之后部组件贮存可靠性的计算方法,可以通过整机可靠性模型将部组件的贮存可靠性转化为发动机的可靠性,从而给出了从材料层次经历多种环境历程后发动机贮存可靠性的通用计算方法。

