循环加载下复合推进剂的非线性热粘弹性本构模型①
童 心,许进升,李 博
(1.中国船舶科学研究中心,无锡 214082;2.南京理工大学 机械工程学院,南京 210094)
0 引言
以固体火箭发动机为动力的空空导弹在完整的寿命期内一般要经历运输、贮存、挂飞、机动飞行和自主飞行等阶段,在长途运输以及挂机飞行过程中的振动频率高达几千赫兹,作为导弹动力装置的固体火箭发动机也随之产生高频振动,发动机内的复合推进剂药柱随着振动载荷的作用会发生疲劳热耗散,导致的温度骤升和热软化效应对发动机的安全性有着显著影响。
由于粘合剂大分子间的缠结、相互吸引以及化学作用,再加上粘合剂分子与填充颗粒间的物理和化学吸附,复合推进剂内部形成了多尺度、多相互作用的多网络结构,力学行为可用非线性粘弹性理论来进行描述。PARK等[1]建立了含损伤热粘弹性本构模型,利用折算时间将不同温度下的材料函数统一至参考温度下,随后HA等[2]将模型拓展为三维形式,HINTERHOELZL等[3]完整地提出了相关的数值算法,将其应用于有限元软件Abaqus,成功地模拟了端羟基聚丁二烯(HTPB)推进剂在单轴和多轴复杂应力条件下的力学响应。张永敬等[4]通过HTPB推进剂蠕变回复实验来拟合了Schapery非线性本构模型的参数,通过与线性粘弹性本构计算的结果和实验数据对比,证明了Schapery非线性本构模型能够很好反映复合推进剂的力学响应。
复合推进剂作为一种温度敏感的颗粒填充类聚合物,其力学表现受到变形中能量耗散的影响,能量耗散的宏观表现是变形过程中自身温度上升[5]。然而,目前大多数非线性粘弹性本构模型的研究仍集中于单纯力学状态的解释与预测,对变形过程中的能量耗散及其影响则关注较少。在高应变率、交变加载等动态条件下,热交换的特征时间比载荷作用时间大几个数量级,由机械功转化而来的热能带来较大的温升,因而材料因变形而生热的性质(自热效应)不容忽视,在这些情况下必须考虑力学耗散引起的热源。由于复合推进剂特殊的组成与结构,这种自热现象在高应变率冲击加载和高频率循环加载下尤为显著。在热力学框架下,材料的时效变形行为本质上是一种非平衡演化过程,在热力学理论框架下建立的本构模型与守恒定律相一致,具有严格的热力学背景和理论基础,不仅满足热力学基本定律,还能表征材料内部的不可逆能量耗散过程和材料的热力学状态、性质[6-8],对热力耦合状态有直观的描述[9]。RODAS等[10]提出了适用于丁苯橡胶有限变形的非线性粘弹性本构模型,以不可逆热力学内变量理论为基础,引入了Helmholtz自由能,并构建了内变量的演化方程,很好地模拟了丁苯橡胶低周疲劳的生热现象。KRAIRI等[11]将总应变分解为粘弹性应变、热应变和粘塑性应变,结合时温等效原理,在不可逆热力学框架下将MILED等[12]的粘弹-粘塑性等温本构模型拓展为非等温形式,发展了热粘弹-粘塑性本构模型,并在热塑性聚合物的有限元仿真中进行了完全耦合形式的热力分析。SHEN等[13]进行了类似工作,模型为热弹-粘塑性本构模型。目前,关于复合推进剂循环加载下的自热效应未见相关报道。
为了精确描述复合推进剂循环加载下的热力耦合特性,本文基于不可逆热力学理论建立了适用于复合推进剂的非线性热粘弹性本构模型,并通过实验验证了模型和数值算法的正确性,本构模型成功表征了复合推进剂在不同加载模式下的非线性力学行为和自热效应,为高能固体聚合物的热力学表征提供参考。
1 本构模型的构建
1.1 非线性热粘弹性本构模型
高分子聚合物材料的力学行为通常具有高度的时间和环境依赖性。Schapery基于不可逆热力学原理,通过引入应力或应变相关标量,使粘弹性模型非线性化,并满足热力学基本定律。因此,该模型也被称为热力学本构模型。在Schapery模型的基础上,提出以下非线性热粘弹性本构模型:
(1)
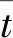
(2a)
(2b)
式中aT为时间-温度等效因子;am为时间-湿度等效因子;aa为时间-老化等效因子。
若湿度等环境因素保持恒定,可认为am=aa=1。本文认为复合推进剂属于各向同性的均质材料,满足连续介质力学的基本假设,因此有
Cve(t,σ)=2G(t,σ)Idev+3K(t,σ)Ivol
(3)
其中,Idev为四阶偏斜张量;Ivol为四阶体积张量;G(t,σ)和K(t,σ)分别为剪切模量和体积模量,具有Prony级数的形式:
(4)
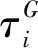
本构模型的关键是选择合适的非线性粘弹性应力函数g1(σ)和g2(σ),它们是构成模型的非线性元素。HAJ-ALI等[14]曾采用多项式形式的应力函数,该函数虽考虑了应力的影响,但函数的参数繁多,难以准确获取。此外,MULIANA等[15]也提出了具有指数形式的非线性函数,但他们所提出的本构模型未应用于循环加载实验。此外,这些模型中函数参数对最终结果的影响不明确。为了克服上述不足,提出具有指数函数形式的非线性应力函数:
(5)
其中,k1、m1、k2、m2和C2为待求参数;σ0为线性粘弹性极限应力,是区分线性粘弹性与非线性粘弹性应力的临界值;σvM为von Mises等效应力,其表达式为
(6)

(7)
综上可知,g1(σ)和g2(σ)是关于应力历史的函数,也是关于时间t的函数。
1.2 产热方程
材料的循环属于不可逆的热力学过程,伴随着能量的耗散,并导致材料自身温度场发生变化。为了描述材料的热力耦合特性,需要建立能量平衡方程。一般情形下,Clausius-Duhem不等式为
(8)
式中q为热流矢量;ψ为Helmholtz自由能;S为熵;T为温度;φ为能量耗散率;φmec为由于外部机械载荷引起的能量耗散率;φT为热耗散率。
结合热力学第一定律可得到:
(9)
因此,产热方程为

(10)
式中 ћ包括热弹性源与内耦合源;φmec为固有耗散转化为热能,即自热效应。
自热效应在高速冲击和高频循环载荷下具有重要的意义。若ћ和φmec均为0,式(10)变为非热力耦合的温度平衡方程,即温度场不受材料本构关系的影响。根据Fourier定律,热流矢量表示为
q=-κ·T
(11)
式中κ为导热张量,若导热是各向同性的,则κ=κl,κ为热导率。
在无外部热源的情况下,rext=0,式(3)变为

(12)
式(12)表明,在无外部热源作用时,材料在循环过程中的温度变化主要受热弹性响应、非弹性响应和热传递(热传导、与环境的热对流及热辐射)三方面的影响。与非弹性耗散源相比,热弹性效应对试件表面温度变化的影响很有限,仅仅引起温度的微小波动;对处于粘弹性变形的复合推进剂而言,内部结构改变不涉及相变,因而内耦合源也可以忽略[16]。
综上所述,在关于复合推进剂能量耗散的分析中,可认为ћ≈0。
1.3 能量耗散
线性热粘弹性本构模型能量耗散φtve的表达式为
φmec=φtve
(13)
其中,φ和m均为松弛函数,反映了温度因素的影响。若温度的变化幅度不大,材料力学特性受温度变化的影响较小,可假设φ和m均为0,则有
(14)
该式与等温条件下线性粘弹性本构模型推导的能量耗散表达式相似,因而:
(15)
式中si和σHj为应力的粘性部分。
LÉVESQUE等[17]已经证明,建立本构模型时在Schapery模型中引入不同的非线性函数依然满足热力学基本定律,且不对Clausius-Duhem不等式产生影响。因此,非线性粘弹性本构模型中的能量耗散采用了和线性模型一致的计算公式。
2 本构模型的二次开发
为模拟聚合物循环过程中的热力耦合,有限元仿真主要采用了下列两种方法:
(1)将材料受载后的自热视为内部热源,通过有限元软件子程序的拓展,先进行力学分析,然后将计算而来的内部热源应用到温度场的求解中[18-19]。RIAHI等[20]、SONG等[21]和LUO等[22]针对不同聚合物材料进行了相关研究。
(2)建立准确可靠的本构模型,通过热力学基本定律,可以从本构模型中获取能量耗散的表达式,从而在有限元分析中同时求解热学和力学问题[23]。依此方法,针对具体研究对象选取适当的自由能函数形式,引入适当的内变量来描述不可逆变形过程中的材料内部微结构的变化,即可获得材料的本构关系,然后就可以从能量平衡方程中推导出热力学变形过程中的温度控制方程[24]。
为了实现完全耦合形式的热力分析,本文选择第二种方法。
2.1 数值算法
应力表达式为σ(t)=s(t)+σH(t)l,其中:
(16)
其中,s∞(t)和σH∞(t)为弹性部分;si(t)和σHj(t)为粘性部分,它们的表达式如下:
(17)
根据gi(σ)的表达式,gi(σ)也是关于t的函数,为了简化,记gi(t)≡gi(σ(t))。给定时间增量[tn,tn+1],则tn+1时的应力偏量s∞(t)为
(18)
si(tn+1)为
(19)
为了获得应力更新方程,令
(20)
由于t=tn+1时应力是未知的,因而gi(tn+1)也是未知的。若时间增量步Δt很小,可以忽略非线性函数在这一时间区间内的变化,作出以下假设:g1(tn+1)≈g1(tn)、g2(tn+1)≈g2(tn)。应力偏量部分可简化为
(21)
其中
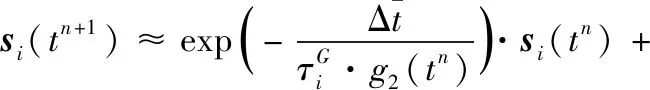
(22)
同样地,对于应力的球量部分,应力更新方程为
(23)
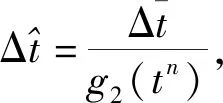
(24)
其中
(25)
综合可得
(26)
其中
(27)
Jacobian矩阵定义为
(28)
2.2 非线性模型子程序
Abaqus拥有用户材料子程序,可方便地对材料本构模型进行二次开发,在高聚物力学特性的数值模拟中得到了广泛的应用。本文选择UMATHT与UMAT联合使用来实现完全耦合的热力分析。在时间增量步中,UMAT通过状态变量“rpl”(rpl的值即为式(12)中的φmec)存储积分点处由于机械加载引起的能量耗散。UMATHT提供了热流矢量,定义了材料的热本构关系,根据产热方程求解热传递问题。图1是执行子程序的流程图。

图1 子程序UMAT和UMATHT流程图Fig.1 Flowchart of UMAT and UMATHT
由于复合推进剂是对温度敏感的材料,应力场和温度场相互影响,因而本文采取了完全耦合的热力分析方法。在完全的热力耦合分析中,耦合方程的矩阵表达式为
(29)
式中 Δu和Δθ分别为位移增量和温度增量;Kij为分矩阵;Ru和Rθ分别为力学和热学残余向量。
3 仿真结果与分析
模型参数的获取方法见文献[25]。利用HTPB推进剂单轴拉伸实验和应变控制的单轴循环实验对本构模型的仿真结果进行验证,试验材料、设备和试验流程的具体说明可参考文献[26],在此不再赘述。仿真时物理模型的几何形状与尺寸与真实哑铃型试件一致,边界条件与实验一致,试件的一端固定,另一端施加位移载荷,见图2,选择试件标距段中部作为分析区域。环境温度根据实验要求设定。试件与环境之间为自然对流换热,试件表面的热边界条件为

图2 Abaqus/CAE中试件边界条件示意图Fig.2 Schematic diagram of boundary conditions of the specimen in Abaqus/CAE
q=-h(Ts-T∞)n
(30)
式中h为试件与环境之间的对流换热系数;Ts为试件表面温度;T∞为环境温度;n为表面的法线方向。
3.1 单轴加载
联合使用子程序UMAT和UMATHT,以模拟复合推进剂由于机械载荷引起的自热效应,探讨其对复合推进剂力学响应的影响。在自热效应的有限元仿真中,UMATHT中的导热系数和比热容是常数,不随温度变化而变化。HTPB推进剂试件与空气之间的对流换热系数h设置为10 W/(m2·K)。
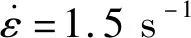

图3 单轴拉伸实验中的自热效应Fig.3 Self-heating effect in uniaxial tensile test
图4显示了自热效应对于单轴应力-应变关系的影响,未考虑自热效应的预测曲线是在等温条件下获取的。由于能量耗散导致了温升,HTPB推进剂受热而软化,因此预测的应力整体偏小。

图4 自热效应对单轴应力-应变关系的影响Fig.4 Effect of self-heating on uniaxial tensile stress-strain relations
为反映自热效应与应变率之间的关系,还进行了常温下其他应变率下的仿真,见图5。随着应变率的提高,外载荷做功越剧烈,能量耗散越来越多,自热效应也越来越显著。该发现揭示了高聚物材料变形中自热效应的应变率相关性,为了更精确地描述材料的力学性能,建立本构模型时需根据变形与加载速率等条件考虑材料自身温度的改变。对复合推进剂而言,在高应变率加载的大应变情形下,自热效应较显著[27]。

图5 不同应变率下的自热效应Fig.5 Self-heating effect under various strain rates
3.2 循环加载
为了明确自热效应对循环行为的影响,随后对受循环加载的HTPB推进剂试件进行了完全热力耦合形式的有限元仿真。图6是试件加载过程中典型的温度云图(加载条件为f=50 Hz,εa=0.03)。可见,试件的标距段的温度由于材料力学耗散而升高,轴向(与试件加载平行的方向)上存在温度梯度,这与实验观测一致。图6中还给出了中心区域截面的温度云图,截面核心温度与边缘温度相差极小,因而可认为试件内部实现了温度平衡,各空间点的温度趋向一致,温度场在这一截面是均匀分布的,这也进一步证明了此前实验分析中利用表面温度表征HTPB推进剂力学性能的合理性。

图6 循环加载中试件典型的温度云图Fig.6 Typical temperature contour of the specimen in cyclic loading
采用对称建模可以减少工作量,既不影响计算结果又可提升计算效率。由于需要同时使用两个子程序,考虑试件的对称性,在后续的仿真中选取试件的一半进行分析。从文献[28]可知,由于HTPB推进剂力学性质的温度相关性,自热效应引起的温升影响着HTPB推进剂动态应力-应变关系的预测。本文进行了多种加载条件下的自热效应模拟,得到了试件标距段表面温度随时间的变化,结果见图7。

(a)Strain amplitude 0.01~0.03
由图7可见,由于开始时试件和环境的温差较小,对流过程中热量损失也比较少,试件的产热速率大于试件和环境的热交换率,因而温度在一段时间逐渐上升;随着循环时间的增加,试件表面温度与环境温度通过热对流而达到平衡,表面温度保持相对稳定的状态。综上,仿真预测结果与实验中测得的温升较吻合,验证了本构模型和数值算法的正确性。
图8给出了不同仿真条件下循环应力-应变关系的对比图。可以发现,与不考虑自热效应相比,滞回圈的斜率降低,表明力学性能已受到自身温度升高的影响。在热力耦合分析中,考虑自热效应后,滞回圈的形状与实验结果更为吻合,非线性热粘弹性本构模型的预测精度得到提高,表明计及自热效应的热力耦合型本构模型能更准确地描述HTPB推进剂的循环力学行为。
为了定量评估模型的预测效果,计算了滞回圈斜率的误差,见图9。由图9可知,模型的预测与实验之间的误差均在10%以内,表明与文献[28]相比,本构模型的预测能力得到了提高,有力佐证了自热效应在本构模型应用中的重要性。

(a)f=10 Hz,εa=0.01 (b)f=1 Hz,εa=0.03 (c)f=10 Hz,εa=0.03

图9 滞回圈斜率的预测误差Fig.9 Prediction errors of the slope of the hysteresis loop
4 结论
(1)对于循环加载下的复合推进剂,自热效应较单轴加载状态更显著(最大温升为15 K),需要在本构模型中加以考虑。
(2)自热效应对复合推进剂的力学行为有着直接影响,与不考虑自热效应相比,循环加载下应力-应变滞回圈的斜率降低,其力学性能的劣化受到自热效应的直接影响。
(3)本构模型成功表征了复合推进剂在不同加载模式下的非线性力学行为和自热效应,模型预测的滞回圈斜率与实验之间的误差均在10%以内。该研究为高能固体聚合物的热力学表征提供了参考。

