基于离散元法苜蓿压扁调制过程仿真分析与试验
王 林,张克平,杨君乾
(甘肃农业大学机电工程学院,兰州 730070)
苜蓿被称为“牧草之王”,是养殖业重要饲草来源,其高效优质生产对调整农牧产业结构、牧草产品精深加工和生态环境优化具有重要影响。实现苜蓿田间收获机械化可提高生产水平及效率,降低人工成本[1-3]。苜蓿胶体物质较多且碳水化合物较少,不易青贮,刈割后需及时晾晒干燥,否则易发霉变质甚至腐烂。苜蓿茎秆和叶片干燥速度不同,田间晾晒过程中叶片先于茎秆达到安全水分,进一步干燥脱水减小茎叶连接力,轻微抖动或搬运造成落叶损失,导致蛋白质含量急剧减少。为实现苜蓿茎秆和叶片同步干燥,田间实际收割时常利用割草压扁机的调制机构对茎秆进行破节、裂皮、压扁、折弯等处理[4-5],以消除或降低茎秆角质层和纤维素在晾晒过程中对水分蒸发的阻碍作用[6-7]。因此,研究并优化调制机构作业性能可有效提升苜蓿草产品质量。
近年来,离散元法(DEM)得到广泛应用,诸多学者将其应用于农业机械设计领域[8-9]。在农作物参数标定方面:廖宜涛、侯杰等分别探究油菜及水稻茎秆离散元接触参数(碰撞恢复系数、静摩擦系数和滚动摩擦系数)[10-11]。马彦华等采用生物力学特性试验和仿真优化相结合方法标定苜蓿茎秆基本接触参数[12]。在农机具性能提升方面:王韦韦等利用离散元软件EDEM建立玉米茎秆模型,模拟茎秆还田后玉米播种器开沟过程,分析该过程中茎秆位移变化,改进开沟器结构[13]。万星宇等以油菜茎秆为研究对象,建立饲用油菜机械化收获切碎过程离散元模型,开展切碎过程离散元仿真研究,优化机械结构和工作参数[14]。郭茜等应用EDEM建立切割粉碎机中番茄茎秆仿真模型,研究茎秆切割时刀片结构参数对茎秆切削效率、切割性能的影响[15]。Bart 等通过EDEM 建立整株稻秆模型,模拟稻秆和谷粒之间摩擦特性,检验稻秆谷粒分离效率,为后期稻秆-土壤-机具之间相互作用研究提供数据支持[16]。Li等运用离散元基本原理建立小段秸秆、谷物、筛子和风机相互作用模型,探究三者耦合作用关系,模拟风机和筛子在清选过程中对谷物和秸秆的相互作用,检验设计机构有效性[17]。
上述研究确定部分农作物参数并提升相关农机具作业性能,研究对象多为油菜、水稻等茎秆,苜蓿茎秆相关研究大多针对其力学特性试验,对茎秆在压扁机中调制程度、受力情况等研究较少。因割草压扁机中茎秆调制过程较复杂,各试验因素对茎秆调制效率及性能等影响较大,本文基于离散元法建立苜蓿茎秆和调制机构模型,采用单因素和响应曲面法进行仿真试验研究,结合台架试验验证,确定试验因素及其交互作用对考核指标的影响规律和最优参数组合,以期为相关农机具设计和优化提供参考依据。
1 压扁调制机构的结构及其工作过程
压扁调制机构是割草压扁机重要组成,作业方式主要包括压扁辊式和连枷式[18],其中压扁辊式在苜蓿调制中应用更广泛,人字型橡胶压扁辊因兼具柔性压扁和钳入功能,是常用核心部件。
压扁调制机构主要由调制辊组合与调节装置组成,如图1所示[19]。
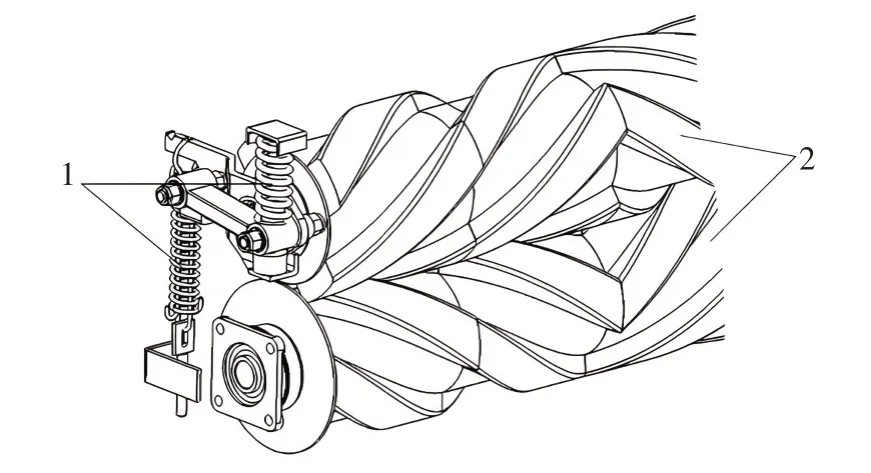
图1 割草压扁调制机构的结构Fig.1 Structure of mowing flattening modulation mechanism
机具工作前,根据田间苜蓿生长状况及饲草调制要求,通过调节装置调整上、下调制辊啮合间隙,机具作业时,切割后苜蓿植株通过导草滚筒输送至调制辊前端,在惯性力和人字形橡胶压扁辊钳入作用下被喂入上、下调制辊间隙,相向转动的调质辊完成对苜蓿植株的压实、精梳和压扁调制,调制后苜蓿草通过调制辊的送料功能被聚拢成一定幅宽的草条均匀铺放在田间。
2 仿真模型建立
2.1 仿真参数确定
采用生物力学特性试验结合仿真试验标定苜蓿茎秆黏结参数。试验样本选用兰州新区收获期紫花苜蓿,挑选无病虫害、无机械损伤的通直主茎秆,将其中部平均含水率为73.2%~74.5%、直径为3.48~3.65 mm、壁厚为0.73~0.78 mm茎秆截成长度为20 mm 无节试样[20]。利用超技质构仪(TA.XT plus,SMS 公司)进行力学特性试验,获得最大径向压力为113.6 N,抗压强度为1.17 MPa,最大载荷为55.2 N,剪切强度为6.92 MPa。
通过EDEM软件进行苜蓿茎秆压缩和剪切仿真模拟试验,根据破坏后的表现特征与实际试验结果对比,确定苜蓿茎秆离散元模型bond 键的黏结参数[21]。苜蓿茎秆力学特性,仿真模拟与试验对比结果如图2所示,仿真压缩试验显示的3个阶段和剪切后茎秆形态与实际试验中压扁及剪切破坏行为一致,此时黏结模型参数表现出的力学形态与在生物力学特性试验中茎秆的实际情况相近。通过对比实际与仿真试验结果,压缩和剪切试验值相对误差分别为7%~11%和8%~15%,证明所建苜蓿空心茎秆分布模型可靠,最终确定Bonding 黏结模型参数:法向刚度系数3.45×108N·m-3,切向刚度系数3.15×108N·m-3,临界法向应力2.32 MPa,临界法向应力7.16 MPa,黏结半径0.54 mm。

图2 苜蓿茎秆力学特性与仿真模拟试验对比Fig.2 Comparison of mechanical characteristics of alfalfa stem and simulation test
2.2 苜蓿茎秆离散元模型
如图3所示,空心茎秆颗粒建模采用圆球颗粒拼接方式,选用“虚实转换”模式建立苜蓿茎秆的三维实体模型(长100 mm、外径3.62 mm、壁厚0.76 mm),由1 533 个半径为0.36 mm 圆球模型拼接填充而成。

图3 空心茎秆模型Fig.3 Hollow stem model
2.3 压扁调制机构模型
为减少仿真试验计算量,利用SolidWorks 软件构建简化模型,将简化几何模型以.step 格式导入EDEM中并完成初始仿真设置。苜蓿茎秆利用颗粒工厂(Factory)的静态方式生成,在生成平面以速率100 个·s-1生成50 个大颗粒,再通过Particle Replacement 完成茎秆模型的替换,确保所有茎秆颗粒在0.1 s 内落在输送带,苜蓿茎秆颗粒及压扁调制机构仿真模型如图4所示。
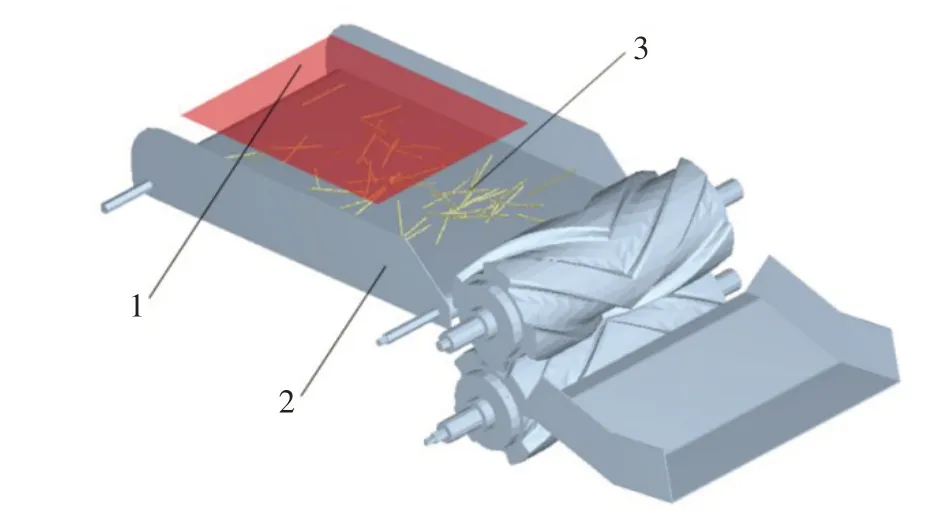
图4 茎秆压扁调制机构仿真模型Fig.4 Simulation model of stem flattening modulation mechanism
在压扁调制作业过程中,茎秆颗粒受压扁、摩擦等作用导致黏结键发生断裂,仿真过程及压力流线型显示如图5所示。图5a为苜蓿茎秆进入调制辊前,两辊之间的高速运动在入口处形成一定压力差,此时茎秆受压最小;图5b 为茎秆进入两辊间,茎秆受压增大;图5c 左半截茎秆处于压扁状态,可明显看出,受压部分压力更大,此时茎秆受压逐步增大;图5d 为茎秆离开两辊间,此时压扁完成将要输出,发现茎秆受压减小变形部分恢复,但受压程度仍大于进入两压扁辊前,此后随惯性作用输送至接料处,完成压扁过程。
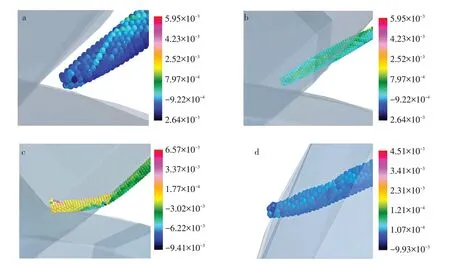
图5 茎秆模型调制过程及压力流线型显示Fig.5 Modulation process and pressure streamline display of stem model
3 压扁调制过程仿真试验与验证
3.1 试验指标
苜蓿茎秆压扁调制装置性能评价标准有压扁率、压扁损失率、粗蛋白含量及单位能耗等,本研究选用压扁率和压扁损失率为仿真试验评价指标。
3.1.1 压扁率
根据国家标准,将每次调制试验后苜蓿长度≥7 cm,且长度50% 以上被压扁的茎秆挑取称量,即为压扁苜蓿质量,其与收获苜蓿总质量之比为苜蓿压扁率,计算公式如下:
式中,Y1为苜蓿压扁率(%);mb为压扁苜蓿质量(g);mz为收获苜蓿总质量(g)。
3.1.2 压扁损失率
将每次调制试验后苜蓿长度<7 cm 茎秆称为碎草,即调制过程中碎草质量与收获苜蓿总质量之比为压扁损失率,计算公式如下:
式中,Y2为压扁损失率(%);mt为碎草质量(g);mz为收获苜蓿总质量(g)。
3.2 单因素试验
影响调制性能的主要因素包括喂入量、调制辊转速及调制辊间隙等[22-24]。为减少仿真试验次数,精准分析各工作参数交互作用,对上述各因素进行单因素仿真试验,探讨试验因素对苜蓿压扁率、压扁损失率的影响规律,确定取值范围。
3.2.1 喂入量
喂入量是影响调制效果重要因素之一,可模拟苜蓿田间长势。仿真试验设定调制辊间隙为3.5 mm,调制辊转速为650 r·min-1,当喂入量在1.0~4.0 kg·s-1区间递增时,获得苜蓿压扁率、压扁损失率变化曲线如图6所示。
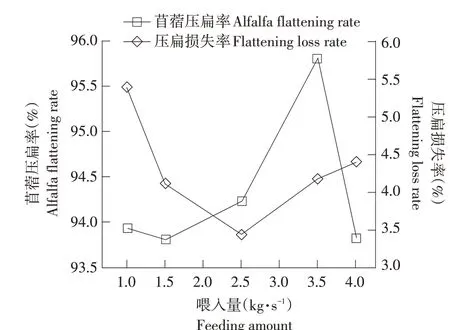
图6 喂入量对调制性能的影响Fig.6 Effects of feeding amount on modulation performance
由图6可知,随喂入量增加,参与调制的苜蓿茎秆逐渐增多,苜蓿压扁率呈先增后减趋势,压扁损失率呈先减后增趋势。喂入量为1.0 kg·s-1时,压扁率较低且损失率较高,调制效果较差,随喂入量增加,效果好转;喂入量为2.5 kg·s-1时,损失率最小,此后开始增长,压扁率处于上升阶段;喂入量为3.5 kg·s-1时,压扁率最大,此后开始下降,而损失率仍呈现增长趋势。随喂入量增加,参与调制的苜蓿茎秆数量逐渐增多,此时单根茎秆所受压扁力降低,造成碎草减少,故压扁率升高,压扁损失率降低;若喂入量持续增加,当茎秆群短时间内打击的力度超过某临界值时,造成茎秆断裂过多,压扁率降低而压扁损失率升高。因此,确定喂入量范围为1.5~3.5 kg·s-1。
3.2.2 调制辊转速
为保证牧草顺利通过调制辊,不出现堵塞和堆积的情况,研究调制辊转速对作业性能的影响规律。仿真试验设定喂入量为2.5 kg·s-1,调制辊间隙为3.5 mm,当调制辊转速在482~818 r·min-1区间递增时,仿真试验获得苜蓿压扁率、压扁损失率变化曲线如图7所示。
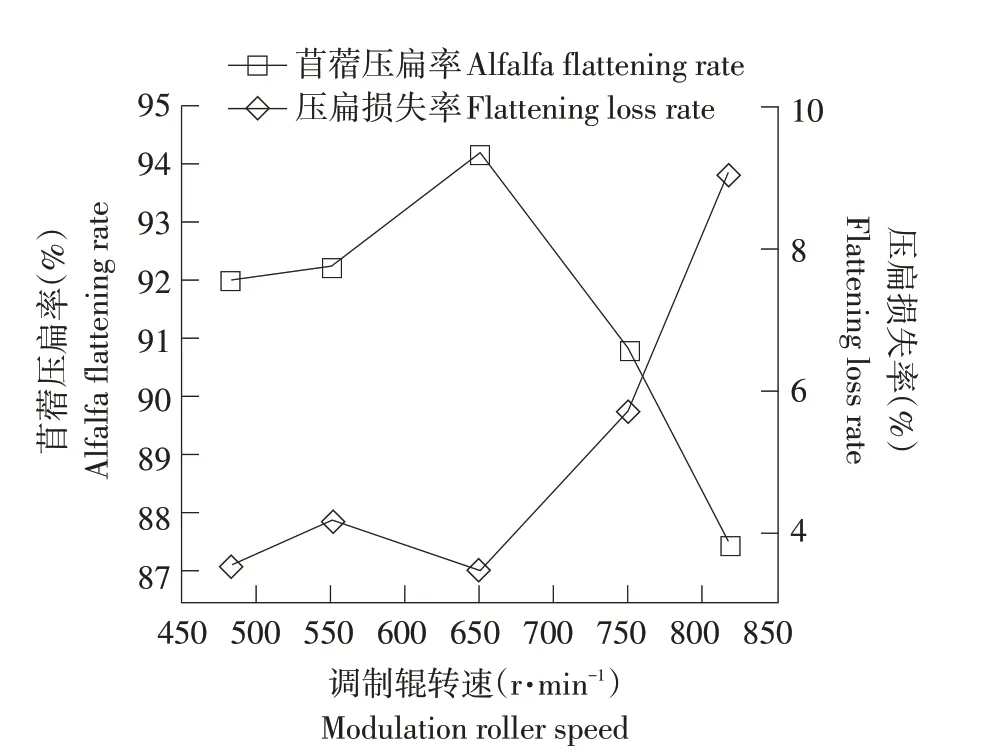
图7 调制辊转速对调制性能的影响Fig.7 Effects of modulation roller speed on modulation performance
由图7可知,随调制辊转速增加,苜蓿压扁率呈先增后减趋势,压扁损失率呈先增后减再增趋势,在调制辊转速为650 r·min-1时,调制效果最好,当调制辊转速由650 r·min-1继续增加时,压扁率开始下降,损失率逐渐上升。调制辊转速过低时,对茎秆群压扁力度较小,产生碎草较少,无法达到调制所需压扁效果,此时压扁率较低、压扁损失率较高;随调制辊转速增加,对茎秆群运动方向的影响逐渐加剧,导致压扁过度,碎草增多,故压扁率降低、压扁损失率增大。综合考虑,确定调制辊转速范围为550~750 r·min-1。
为进一步分析调质辊转速对茎秆压扁过程的影响,获取转速分别为550、650 和750 r·min-1时茎秆运行速度分布,如图8所示。
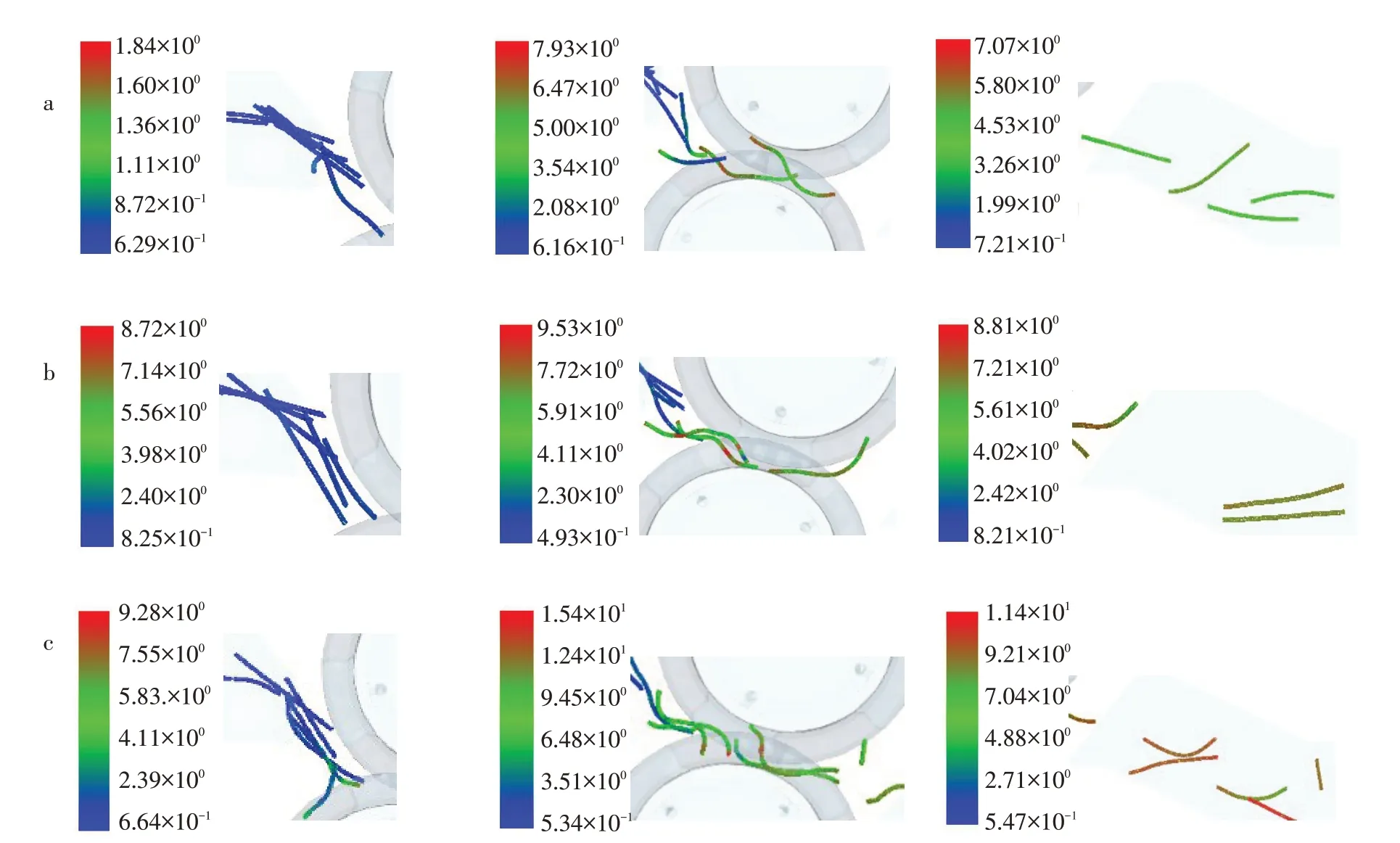
图8 不同调制辊转速时茎秆运行速度Fig.8 Stem running speed with different modulation roller gap
由图8可知,不同调制辊转速对应茎秆运行速度差别明显,当调制辊转速为550 r·min-1时,3 个阶段茎秆运行速度均为最低,随辊转速逐步增加,茎秆运行速度也增加;从调制过程分析,喂入前茎秆运行速度最低,在调制进行时茎秆速度达到最高,调制完成后茎秆速度降低但远大于喂入前运行速度,同时验证仿真结果真实性和可靠性。
3.2.3 调制辊间隙
调制辊间隙对茎秆压扁程度及调制性能均有较大影响。仿真试验设定喂入量为2.5 kg·s-1,调制辊转速为650 r·min-1,当调制辊间隙在2~5 mm区间递增时,仿真试验获得苜蓿压扁率、压扁损失率变化曲线如图9所示。
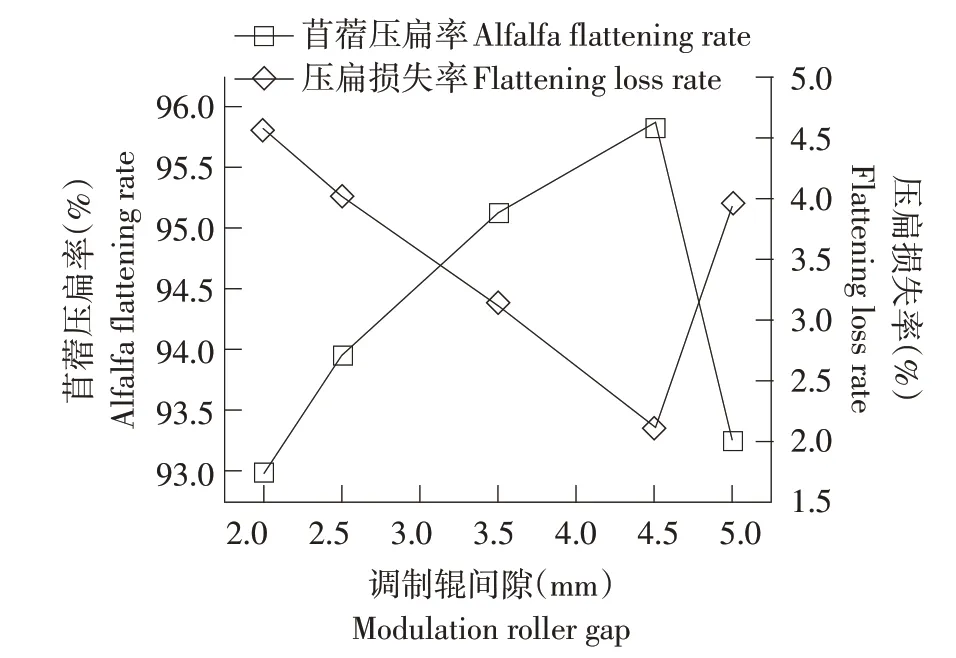
图9 调制辊间隙对调制性能的影响Fig.9 Effects of modulation roller gap on modulation performance
由图9可知,随调制辊间隙增加,苜蓿压扁率呈先增后减趋势,压扁损失率呈先减后增趋势;当调制辊间隙由2.0 mm 增至4.5 mm 时,压扁率和碎草率均明显改善。这是因为随调制辊间隙增大,辊齿对茎秆群打击面积和力度也相对增大;当调制辊间隙过小,为2.0 mm时,通过茎秆群较少,因茎秆直径小于此时的调制辊间隙,易造成压扁过度及产生过多碎草,导致压扁率较低、压扁损失率较高;当调制辊间隙增加至4.5 mm 时,其内部空间可容纳苜蓿茎秆数量逐步增多,两辊齿之间压扁力度也可达到预期调制效果,产生碎草较少,此时压扁率较高,压扁损失率较低。因此综合考虑调制辊间隙应取2.5~4.5 mm。
3.3 响应面仿真试验与分析
3.3.1 试验方案
综合单因素试验为研究不同试验因素对苜蓿压扁调制质量的影响程度及各因素交互作用,采用三因素三水平Box-Behnken试验设计方法进行响应面试验。
以喂入量X1、调制辊转速X2和调制辊间隙X3为自变量,苜蓿压扁率Y1和压扁损失率Y2为响应值,各试验因素编码见表1。根据设计方案在EDEM中进行仿真试验,试验方案及结果见表2。
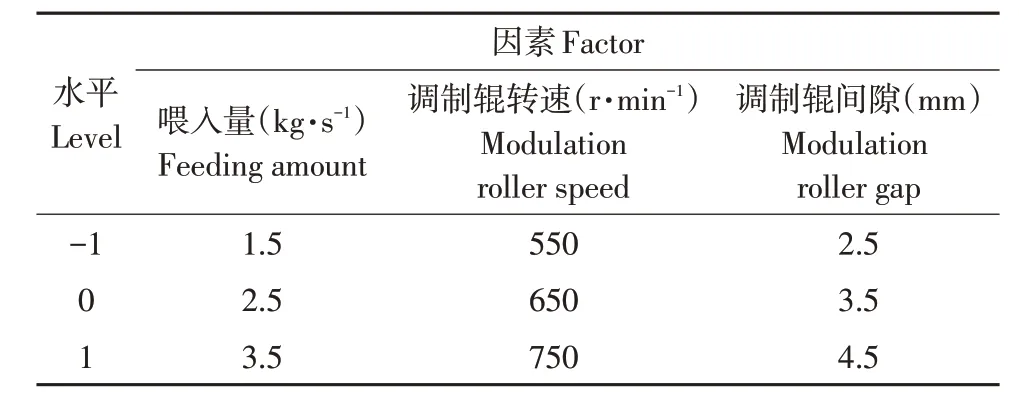
表1 试验因素编码Table 1 Coding of test factors
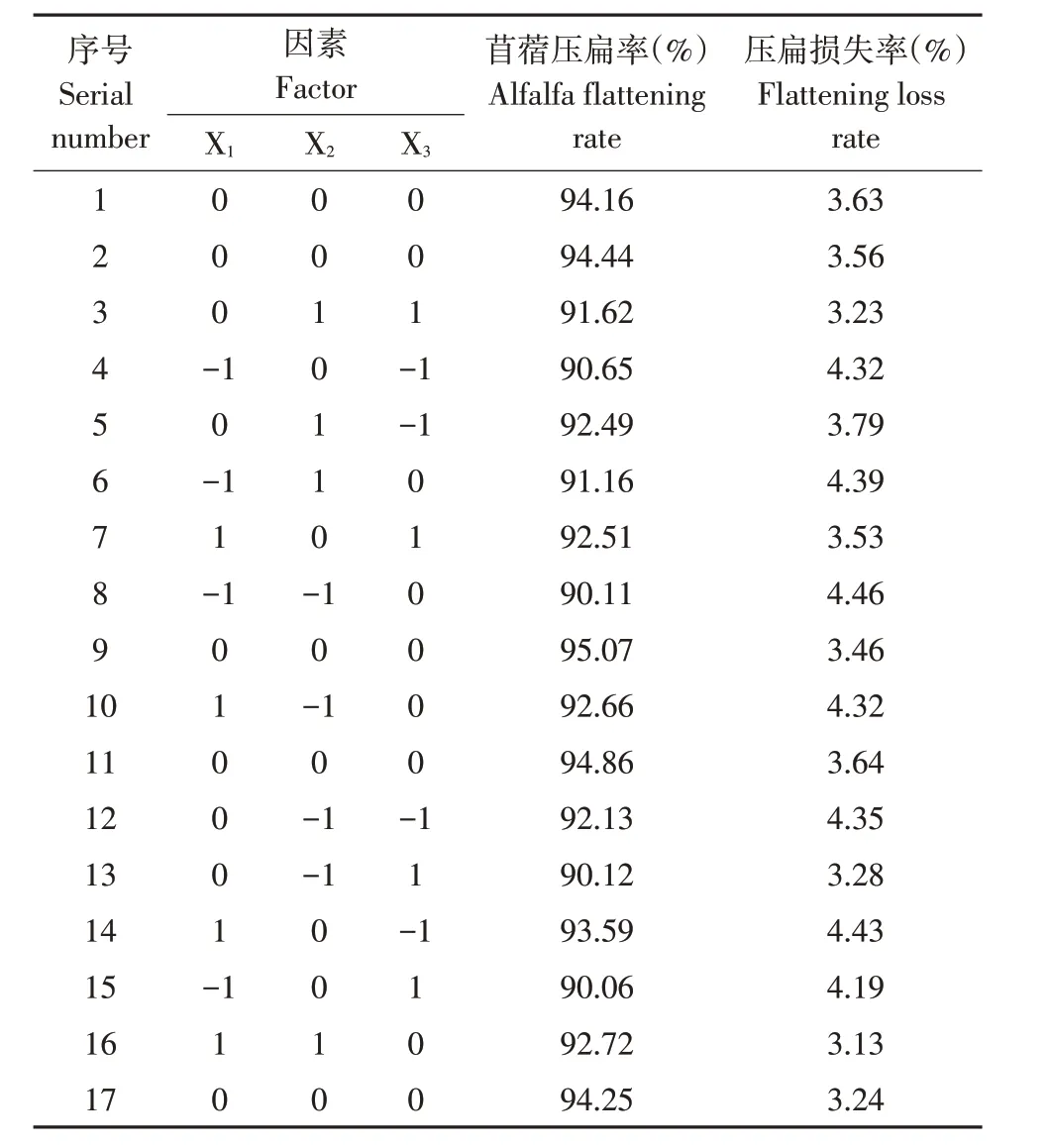
表2 试验方案及结果Table 2 Factors and codes of alfalfa conditioning test
3.3.2 回归模型建立与显著性检验
利用Design-Expert 11 软件对苜蓿压扁率Y1和压扁损失率Y2回归模型进行方差分析,如表3 所示,建立各项评价指标与试验因素之间二次回归方程模型如式3、4所示。
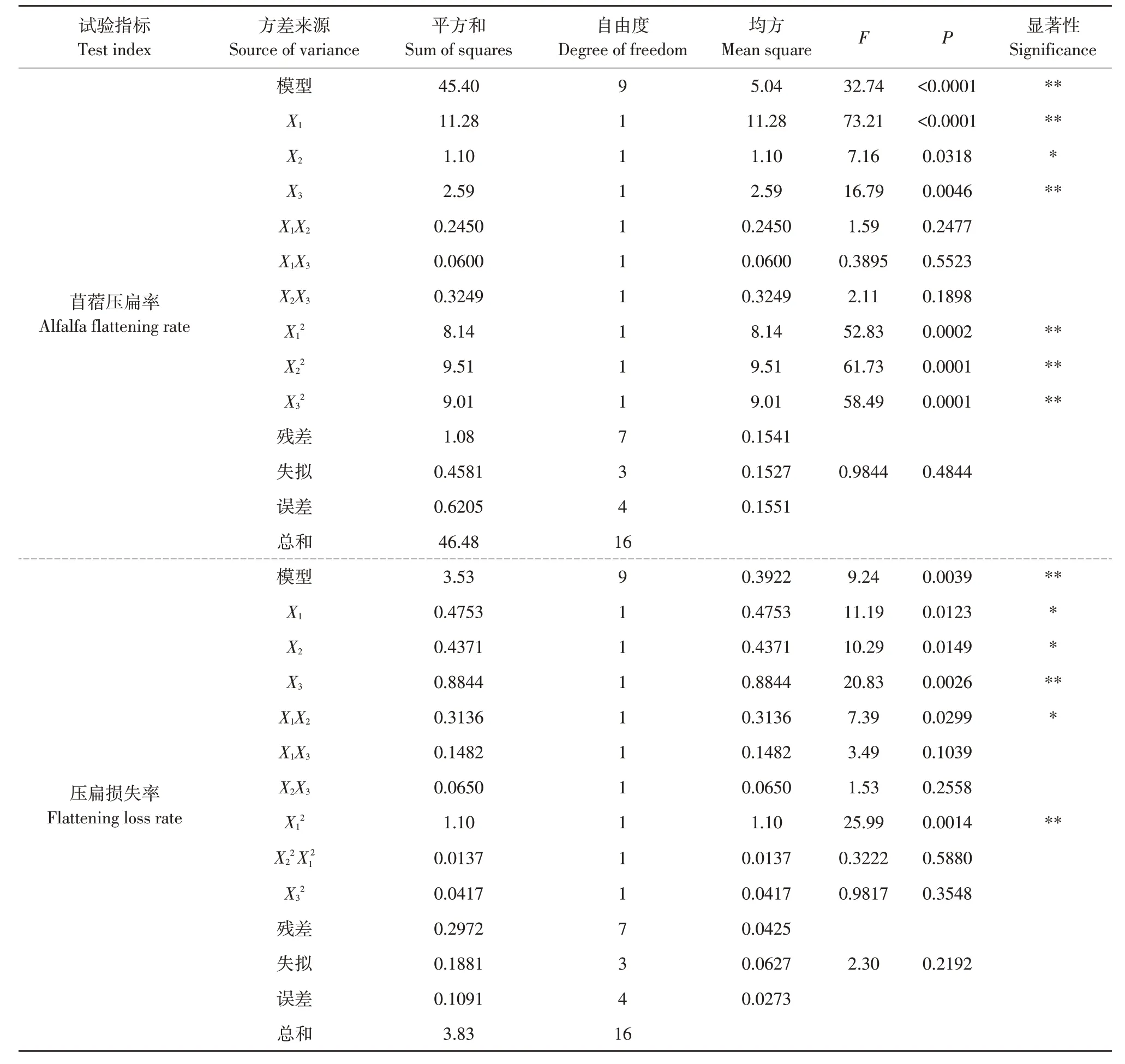
表3 回归方程方差分析Table 3 Variance analysis of regression equation
由表3可知,苜蓿压扁率Y1和压扁损失率Y2与试验因素的回归模型P<0.0001和P<0.0039(均小于0.01),表明模型极显著;失拟项P值分别为0.4844、0.2192(均大于0.05),表明无失拟因素存在,两个模型在试验参数范围内,拟合程度较高,可较好预测优化试验中各种试验结果;模型决定系数R2分别为0.9768、0.9223,表明该模型可较好解释不同因素作用下响应值,预测试验台工作参数。
此外,在苜蓿压扁率Y1回归模型中,因素X1、X3、X12、X22、X32对模型影响极显著,因素X2对模型影响显著;在压扁损失率Y2回归模型中,因素X3、X12对模型影响极显著,因素X1、X2、X1X2对模型影响显著;根据模型各因素回归系数大小,可得到各因素对苜蓿压扁率影响主次顺序为:X1、X3、X2,即喂入量、调制辊间隙、调制辊转速;对压扁损失率影响主次顺序为:X3、X1、X2,即调制辊间隙、喂入量、调制辊转速。
3.3.3 试验因素对性能指标的影响
根据表3 试验结果,分析喂入量、调制辊转速、调制辊间隙及其交互作用对各性能指标的影响,利用Design-Expert 11 软件进行响应面分析,根据建立的回归模型分别获得各因素之间交互作用响应曲面图。
3.3.3.1 苜蓿压扁率
各试验因素对苜蓿压扁率交互的影响如图10所示。
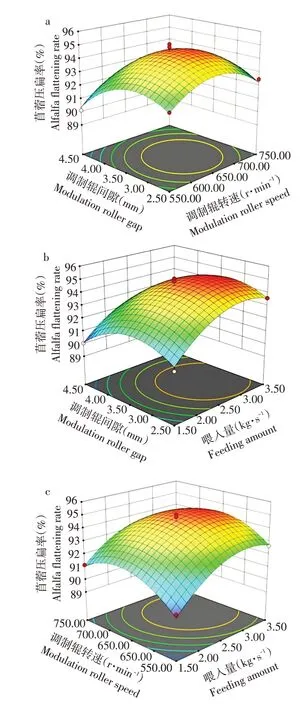
图10 各试验因素对苜蓿压扁率的交互影响Fig.10 Interaction effect of various experimental factors on alfalfa flattening rate
由图10a 可知,当喂入量固定在某一水平时,苜蓿压扁率随调制辊转速增加,先升后降;当调制辊转速固定在某一水平时,苜蓿压扁率随喂入量增加,先升后降;由响应曲面变化趋势可见喂入量对压扁率的影响高于辊转速,这是因为调制辊做功主要集中在苜蓿之间的相对位移和摩擦上,当喂入量增加时,茎秆贴合性增强,体积横量此时变大,被压实的茎秆相互贴紧堆砌产生塑性形变。
由图10b 可知,当调制辊间隙固定在某一水平时,苜蓿压扁率随调制辊转速增加,先升后降;当调制辊转速固定在某一水平时,苜蓿压扁率随调制辊间隙增加,先升后降;由响应曲面变化趋势可知调制辊间隙对苜蓿压扁率的影响显著高于调制辊转速,这是因苜蓿在未经调制时排列相对松散,苜蓿之间存在间隙,当调制辊间隙较大时,人字形调制辊压扁苜蓿具有随机性,此时苜蓿受压不均匀,无法保证每根苜蓿均被压扁。
由图10c可知,当调制辊间隙固定在某一水平时,苜蓿压扁率随喂入量增加而增加;当喂入量固定在某一水平时,苜蓿压扁率随调制辊间隙增加,先升后降,由响应面变化趋势可知,喂入量对苜蓿压扁率影响显著高于调制辊间隙。
3.3.3.2 压扁损失率
各试验因素对压扁损失率的交互影响如图11所示。
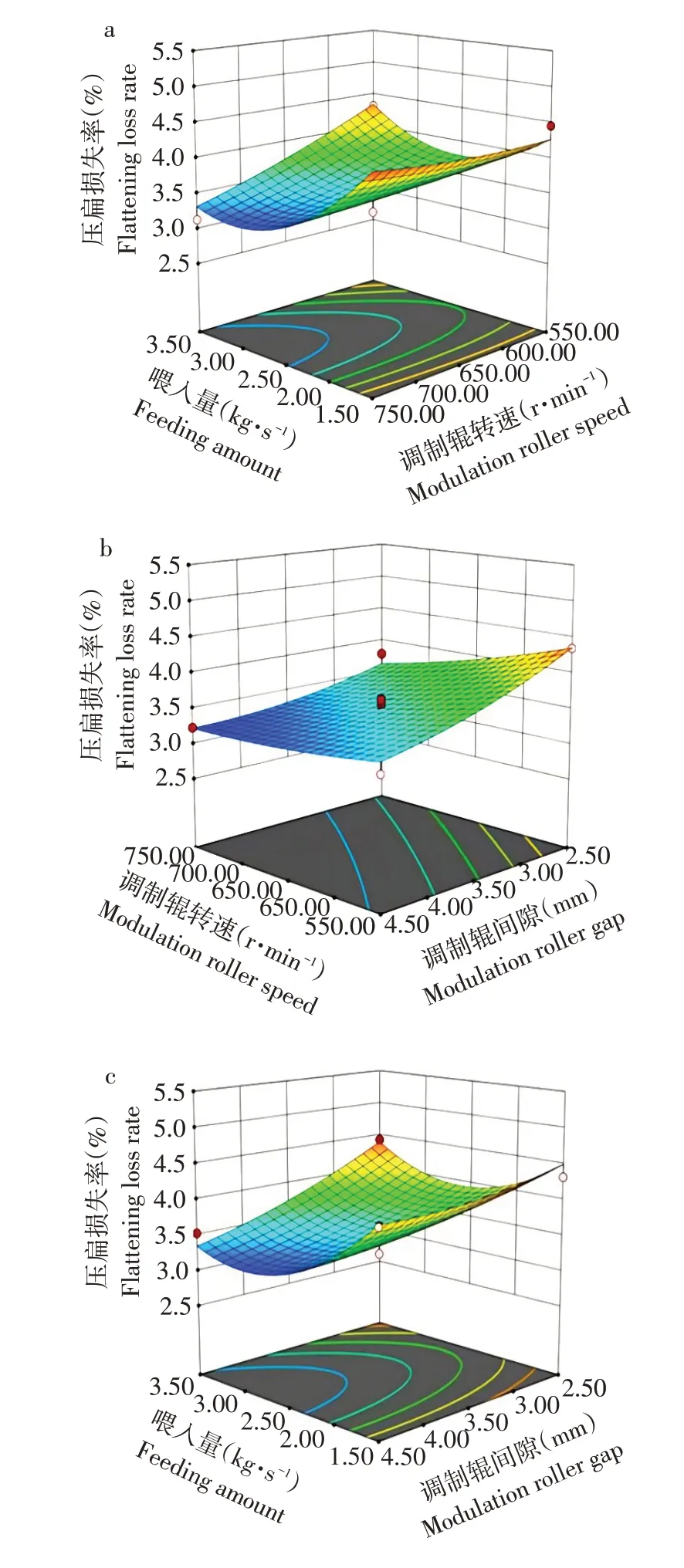
图11 各试验因素对压扁损失率的交互影响Fig.11 Interaction effect of various experimental factors on the flattening loss rate
由图11a 可知,当喂入量固定在某一水平时,压扁损失率随调制辊转速增加整体呈上升趋势;当调制辊转速固定在某一水平时,压扁损失率随喂入量增加先降后升,其响应曲面较陡,喂入量与调制辊转速交互作用对压扁损失率影响显著,与方差分析结果相同,由响应面变化趋势可知喂入量对压扁损失率影响明显高于调制辊转速。
由图11b可知,当调制辊转速固定在某一水平时,压扁损失率随调制辊间隙增加而降低;调制辊间隙固定在某一水平时,压扁损失率随调制辊转速增加先降后升,由响应面变化趋势可知调制辊间隙对压扁损失率影响高于调制辊转速。
由图11c 可知,当喂入量固定在某一水平时,压扁损失率随调制辊间隙增加而降低;当调制辊间隙固定在某一水平时,压扁损失率随调制辊间隙增加先降后升,由响应面变化趋势可知可调制辊间隙对压扁损失率的影响高于喂入量。
3.3.4 最优工作参数确定
根据上述试验结果分析,为进一步提升苜蓿压扁率,降低压扁损失率,需确定影响该性能最优参数组合。在各试验因素水平约束条件下,以最高苜蓿压扁率Y1和最低压扁损失率Y2作为优化指标,建立性能指标全因子二次回归方程,进行目标优化及最优工作参数确定。
应用Design-Expert 11 软件中优化求解器对回归方程进行该目标下优化求解,得到最优工作参数组合:喂入量2.89 kg·s-1、调制辊转速693.91 r·min-1、调制辊间隙3.72 mm。但因调制机构实际工作参数较难调整至理论求解的优化值,故选取一组接近于优化求解值的参数进行试验验证,参数值取:喂入量2.9 kg·s-1、调制辊转速694 r·min-1、调制辊间隙3.7 mm,其中,苜蓿压扁率重要度为+++++,压扁损失率重要度为+++++,代入模型中求解得苜蓿压扁率Y1为94.45%、压扁损失率Y2为3.27%。
3.4 台架试验验证
为验证所建立回归模型及仿真试验结果可靠性,设计制造苜蓿压扁调制试验台如图12a 所示,其中电动机固定安装在机架左侧的下横梁上与变频器相连,实现输出转速无级调节,为苜蓿压扁调制试验台的工作提供动力;通过输送带连接安装在机架和间距调节架上的两输送带托辊,实现苜蓿输送和喂料量调节功能;两调制辊通过轴承座分别安装在间距调节架和机架下梁上,实现苜蓿的压扁调制;出料板固定安装在右机架侧梁上,实现压扁后苜蓿输出。

图12 苜蓿调制试验台结构与台架验证Fig.12 Structure drawing of alfalfa mixing experimental bench and bench validation
利用苜蓿压扁调制试验台按照上述最优工作参数组合进行作业性能试验。试验选取的苜蓿为初花期,其中部平均含水率为68%~74%,直径为2.8~3.6 mm,试样高度为30~45 cm,所需仪器及工具为游标卡尺、米尺、分析天平(精度0.1 mg)。试验过程如图12b所示,试验共5次,依据评价指标公式计算,得到5次试验下苜蓿压扁率为93.21%,压扁损失率为3.35%。
如图12b所示,通过现场结果可直观看出,苜蓿压扁调制后可分为碎草与压扁状态。因验证试验采用的苜蓿试样直径与长度不一致,且计算机精度远高于人工试验,故试验结果与理论优化值之间存在一定差异,但两者相对误差均小于3%。
4 结 论
a.利用EDEM软件建立苜蓿茎秆和压扁调制机构离散元仿真模型,按照Box-Behnken试验设计原理,采用三因素三水平响应曲面方法完成离散元仿真试验,结果表明,影响苜蓿压扁率与压扁损失率的因素主次顺序由大到小分别为喂入量、调制辊间隙、调制辊转速和调制辊间隙、喂入量、调制辊转速。
b.建立苜蓿压扁率、压扁损失率与喂入量、调制辊转速、调制辊间隙二次多项式回归模型,以苜蓿压扁率最高和压扁损失率最低为目标,得出最优解为:喂入量2.9 kg·s-1、调制辊转速694 r·min-1、调制辊间隙3.7 mm,此时苜蓿压扁率为94.45%、压扁损失率为3.27%。台架试验验证表明,试验值与理论优化值之间相对误差小于3%,回归模型可靠,可为相关机具设计和优化提供数据参考和理论依据。

