广义线性模型的分位数回归变点检测 *
王丽梅
(广西师范大学 数学与统计学院,广西 桂林 541004)
0 引言
变点问题因其具有广泛应用性,比如在金融、经济、计算机等都有大量的应用,所以在统计学中一直是研究的热门课题。变点指的是在模型或者分布中,在某个未知的时刻,模型或者分布的某些特征发生改变,则把这个未知的时刻称为变点。
目前,对变点问题研究的文献有很多。如谭智平等人[1]利用非参数方法构建Kolmogorov 型统计量对分布变点的检测和估计进行研究;Guan[2]通过似然比方法研究半参数模型的变点问题;张军舰等人[3]通过构造截断经验欧氏似然比检验函数对均值单变点模型的变点位置进行估计;Bai[4]利用残差的经验分布函数对线性模型的结构变点进行研究;Harachaoui 和Levy-Leduce[5]首次将变点的估计问题转换为基于LASSO 方法的线性回归中的变量选择问题。自从Koenker 和Bassett[6]提出分位数回归的思想,就有许多学者将分位数回归与变点结合起来,如Qu[7]基于子样本的次梯度构造检验统计量和Wald 型统计量讨论了线性分位数回归模型的结构变点检测问题;Li[8]讨论了折线分位数回归模型的变点估计问题;张立文[9]研究了在数据存在删失的情况下线性分位数回归模型的变点检测问题;Zhou[10]的第二章是基于次梯度的思想构造检验统计量检测线性分位数回归模型的实时变点。但是,目前存在的变点研究文献中,对于广义线性模型的分位数回归变点研究还较少,如Xia[11]利用加权残差来构造检验统计量研究了广义线性模型的实时变点;但是由于在小样本情况下,此文章提出的方法犯第一轮错误效果不好,所以Zhou[10]的第三章利用Bootstrap 方法改进了Xia[11]中存在的问题。
本文在Qu[7]的基础上,利用子样本的次梯度构造检验统计量检测广义线性模型是否存在变点。第二节主要介绍模型及其检验统计量的构造,第三节为数值模拟,第四节证明相关引理和定理,第五节是本文的总结。
1 模型与主要结果
{(yi,xi),i= 1,…,n} 是一列来自总体(Y,X) 的独立同分布随机样本,yi是一维响应变量,xi是一个p×1维的协变量。考虑如下的广义线性模型:
假设yi的条件密度函数服从指数族分布,即
其中a(·),b(·),c(·)是已知函数,φ是离散参数,代表尺度;θ称为规范参数,代表位置。且yi的条件均值为
其中,βi是p维未知参数,g-1( ⋅ )是一个已知的合适的连接函数。则
εi是模型的随机误差,对于给定的分位数水平τ∈( 0,1 ),满足p(εi<0|xi)=τ。所以对于给定的xi,yi的条件τ分位数为:
这里Qy(τ|x)= inf {t:Fy(t|x)≥τ}是给定x的情况下y的条件分位数。
本文感兴趣的是对于给定的分位数τ,在连接函数g-1( ⋅ )不变的情况下检验参数β是否发生改变,也即考虑如下的检验:
其中,β0,τ为未知的真实参数,β1,τ≠β2,τ,n1为未知的变点,β1,τ,β2,τ分别是变点前后的未知参数。β0,τ的估计可以由下式得到
其中ρτ(u)=u(1 -I(u<0 )),I(u<0 )是示性函数。
基于文献[7]构造检验统计量的思想,本文利用子样本来计算次梯度。定义:
其中g′( ⋅ )是函数g( ⋅ )的一阶导数,0 ≤λ≤1,[x]为取整函数以及ψτ(u)=τ-I(u<0 )。
由于变点的位置未知,所以需要搜索所有可能的点。基于此,给出本文的检验统计量:
其中,|| ⋅||∞表示上确界函数,例如a=(a1,a2,…,ap),||a||∞= max (|a1|,|a2|,…,|ap|),
当在原假设下即变点不存在时,ψτ(u)=τ-I(u<0 )是一个均值为0 方差为τ(1 -τ)的二元独立随机变量序列,所以会收敛到一个均值为0 的高斯过程;而在备择假设下即存在一个变点时,因为与变点前后的真实参数有较大的差异,如果仍然使用来代替变点前后的真实参数就会使得估计的模型残差一致低于或者高于真实的分位数,从而使得统计量取得较大的值。
定义f( ⋅ |X)和F( ⋅ |X)分别是给定X条件下Y的条件密度函数和条件分布函数。为书写简便,记f( ⋅ |xi)和F( ⋅ |x i)分别为fi( ⋅ )和Fi( ⋅ )。为了得到检验统计量的渐进性质,本文给出了如下的假设:
假设1条件密度函数fi( ⋅ )在点处一致远离0 和∞。
假设2函数g( ⋅ )是单调连续且二阶可微的,g′( ⋅ )有界,g″( ⋅ )有界。
假设3,对任意的
假设4是一个p×p维非随机有限正定矩阵
其中假设1 是分位数回归中的一般假设,假设2 和假设3 保证了目标函数(1)有唯一解,且由假设3 可以得到
引理1在假设1~4 下,当原假设H0成立时,有
引理2在假设1~4 下,当原假设H0成立时,对任意的紧集D∈Rp,有
定理1在假设1~4 下,当原假设H0成立时,有其中,Bp(λ)是一个p维独立布朗桥。
2 数值模拟
本文在备择假设H1即模型存在变点时模拟检验统计量的功效,数据来自于下面的泊松回归模型:
xi~U( 0,1 ),d表示斜率参数改变的大小,d= 0 代表泊松回归模型不存在变点,d模拟时分别取1,2,3;分位数τ分别取0.25,0.5,0.75,分别对应低分位数、中分位数和高分位数;显著性水平α为0.05;样本量设为n=100 和300;变点位置分别设为n1=n/4,n/2,3n/4。在所有的模拟过程中模拟重复1000 次。模拟效果如表1所示。
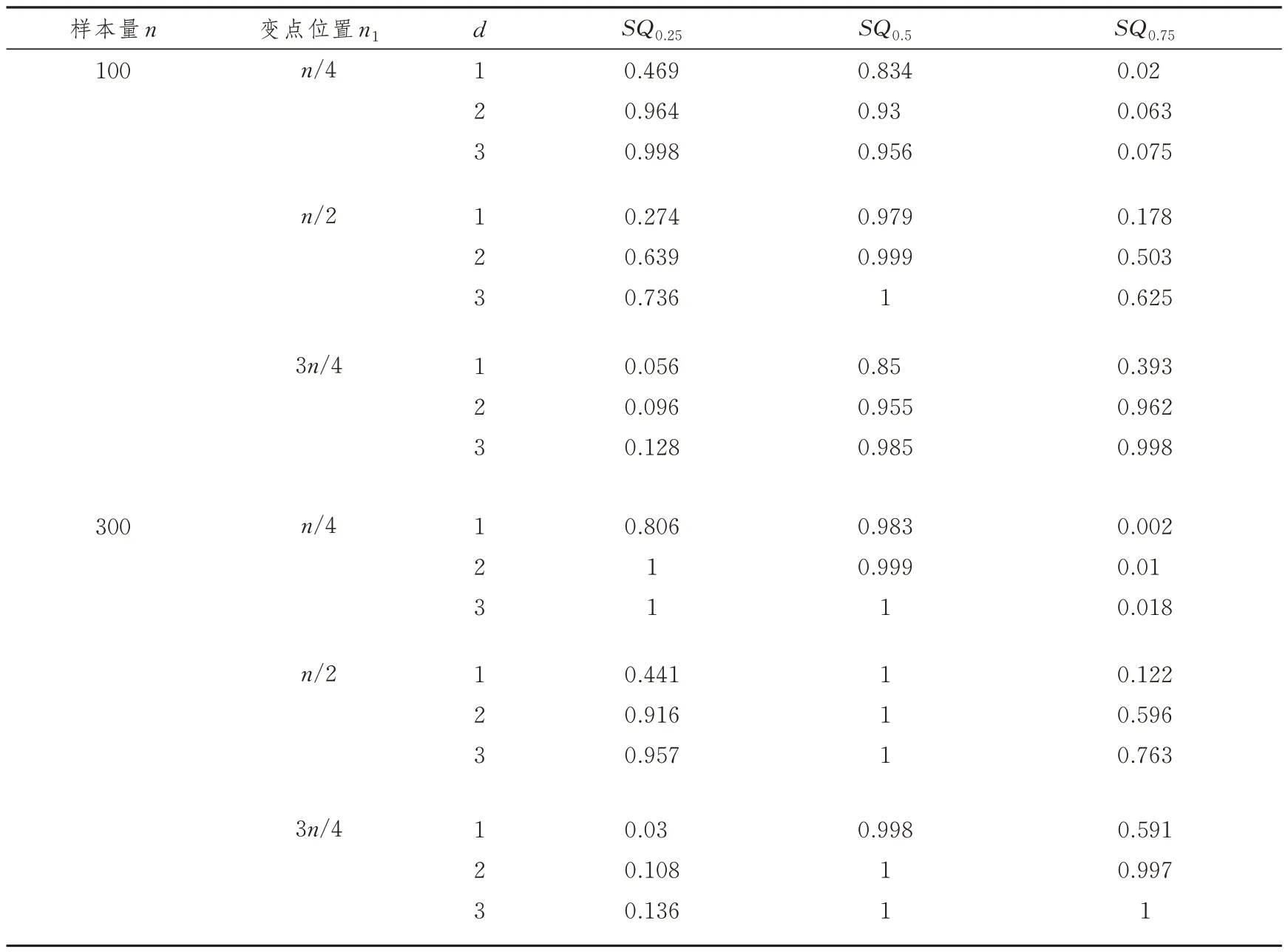
表1 有限样本在名义水平为0.05 的功效
对照n= 100 和300,可看出随着样本容量的增加,各分位数下的检验统计量功效都更加接近1;同样当斜率参数d变化幅度变大时,也逐渐趋于1,这表明检验效果也更好。对应低分位数SQ0.25来说,变点位置越靠前其检验效果越好;反之,对于高分位数SQ0.75来说,变点位置越靠后其检验效果越好。总体来看,检验统计量的检验功效良好。
3 理论证明
3.1 证明引理1
又因为Z0(ξ)是一个凸函数,所以存在唯一最小值为,故所以
3.2 证明引理2
不失一般性,假设xi的元素都是非负的,函数g( ⋅ ) 是单调递增函数是非负的,则是关于ξ的非降函数。由于D是紧集,所以对于任意的δ>0,D可以分割为n(δ) 个直径小于等于δ的有限个子集D1,…,Dn(δ)。对于任意的ξ∈Dh,h∈{ 1,…,n(δ) },存在Dh中的两点ξh,1和ξh,2使得由的单调性,有
同理可得
根据(10)式和(11)式得
对于(b)项,将在点处一阶泰勒展开,由假设1~3 得(b)=δOp(1 ),当δ充分小时
对于(a)项,只需证因为
是一个鞅差序列,所以利用Doob 不等式和Rosenthal 不等式,存在常数M1和M2,对任意的λ>1,根据假设1~3 有
所以(a)=op(1 ),根据(13)~(15)式引理2 证明完毕。
证明定理1:
由引理2 得
所以
其中,Wp( ⋅ )是一个p维独立维纳过程,所以定理1 证明完毕。
4 总结
本文结合分位数回归的思想,将文献[7]的线性模型扩展到使用范围更加广泛的广义线性模型,考虑在其连接函数不变的情况下参数是否发生改变,利用子样本的次梯度来构造检验统计量,并且找到了在原假设下检验统计量的渐进分布,并通过数值模拟证明了该检验的有效性。

