基于半定规划的多约束图划分问题

王晓瑜,刘红卫,王 婷,丁玉婉,游海龙

(1.西安电子科技大学 数学与统计学院,西安 710126; 2.西安电子科技大学 微电子学院,西安 710071)

超大规模集成电路(VLSI)设计[1]、电信[2]和并行运算[3]等问题在数学建模时通常被抽象为图的形式,图分割是其基本算法之一.但随着数据规模的不断增长,图划分问题变得更具有多面性和挑战性.该问题旨在将图G=(V,E)的顶点在一定容量或基数的约束下划分为几个组,使得所求最优解的割边总权重最小.由于该问题是NP-完备的,因此研究寻找近似解的方法有一定的意义.

图划分问题源于针对图的k划分问题设计的一个二次程序.随着新的图划分问题的不断发展,多种求解方法也应时而生,例如: Kernighan等[4]考虑将图划分为给定大小的子集,并设计了一种启发式方法进行求解; Christofides等[5]对图的二分问题提出了树搜索方法,有效地限制了子集中节点的数目; Labbé等[6]针对团划分问题,利用分支定界算法将图划分为有上下界的子集.

通过将图划分问题重新表述为一个非凸二次规划问题,人们提出了一些有效的近似算法.Goemans等[7]对非负加权图提出了基于半定松弛的舍入算法,该算法对k=2可实现0.878的近似界; Frieze等[8]针对图的多分问题扩展了文献[7]的舍入算法,并分析了所设计算法在不同划分块下的理论近似比.在近似算法的基础上,分支定界法也被设计用于求解图划分问题.Rendl等[9]利用基于半定松弛的分支定界算法Biq Mac求解了经典的最大割问题; Delling等[10]根据分支定界框架提出了求解最小图二分的精确组合算法,其下界是通过启发式方法得到的; Lu等[11]提出了一种新的分支定界算法,直接选择一个合适的向量生成k个子问题,设计了减少枚举过程中子问题冗余性的策略.

背包问题作为组合优化问题的基本问题之一,已在多学科领域得到广泛研究.本文主要关注具有背包约束的图划分(GPKC)问题,图中的每个顶点都被赋予一个权值,每个划分集合都需满足背包约束.Recalde等[12]将背包问题转化为整数规划问题,并设计了一种基于分支定界的精确算法来求解该问题.Nguyen[13]针对GPKC问题提出了一个严格的LP松弛方法,并利用启发式方法建立解的上界.由于基于半定规划在生成具有背包约束[14]和k-均分问题的二次问题紧下界方面性能较好,因此研究者们将半定规划松弛应用于GPKC问题中.Wiegele等[15]通过引入带有非负约束的紧的半定松弛,得到了多达500个顶点的GPKC问题的高质量下界,同时,所设计的启发式算法相比于文献[13]可得到一个更严格的上界,但该算法尚未考虑在给定划分块数的情形下是否能满足划分结果.

对于大规模划分的实际应用,也可考虑将启发式和元启发式方法用于寻找足够好的次优解.Arriz等[16]将模拟退火和禁忌搜索方法相结合求解图二分问题,其算法可花费较小的计算代价而得到高质量的解.Benlic等[17]基于多级划分和禁忌搜索提出了一种混合算法,把禁忌搜索作为多级框架的细化算法,用于解决图的平衡划分问题,其算法性能优于图划分软件Metis和Chaco.

基于此,本文考虑带有顶点权重约束的图的二划分问题,利用图的二划分方法递归地进行图的多分,并将所设计的算法与Wiegele等[15]提出的图的多分算法进行比较,验证该算法的有效性.

1 图的二划分

1.1 模型的建立

给定一个赋权无向图G=(V,E),其中V={1,2,…,n}为点集,n为图G中的顶点个数,E为边集,W为图G的邻接矩阵,ωij为对应边[i,j]∈E的权值,则∀i≠j,有ωij=ωji,且ωii=0.记bi为顶点i的非负权重,U为划分集合容量上限.GPKC问题要求将图的顶点V划分为两部分,即S和VS,使得在不同集合中的顶点满足切边总权重最小,且每组的顶点权重和不超过容量上限U,则目标函数可写为

(1)

令xi表示顶点i,若顶点i属于集合S,则xi取值为1,反之,xi取值为-1.于是未考虑顶点权重约束的图二划分问题可写为如下二次函数形式:

(2)

引入与W相关的Laplace矩阵L=diag(We)-W,其中e∈n是一个分量全为1的列向量,diag(We)是一个对角矩阵,其对角项为向量We中的元素.于是图二划分模型(2)等价于如下二次整数规划形式(IQP):

令B表示顶点的权重向量,则第i个顶点的权重为bi,U=(u1,u2)T表示划分集合的资源上限,ur(r∈{1,2})表示第r块划分集合的上限,则求解模型(GPKC)为

xTLx=tr(xTLx)=tr(LxxT)=tr(LX),

(3)

因此利用文献[18]中矩阵迹运算的性质,可将问题(GPKC)重写为

(4)

其中矩阵

(5)

是半正定的秩1矩阵,且对角线元素均为1.

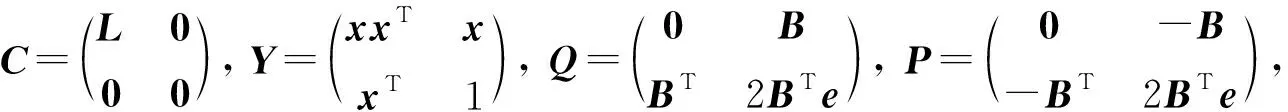
上述半定规划松弛模型(GPKC1)求解较复杂,但在不考虑顶点权重约束的情形下,原问题可行,半定规划及其对应的对偶模型是严格可行的,且易找到其严格可行点,因此本文考虑使用内点法求解去掉顶点权重约束的更松弛的半定规划,再对求得的解进行随机扰动,并在随机扰动过程中增加对解的可行性判定,以保证所得解满足顶点权重约束.

去掉顶点权重约束的半定规划松弛模型(SDP)为

其对应的对偶形式(DSDP)为

本文采用内点法[19]求解模型(SDP)和(DSDP),起始点Y∶=In×n,y∶=μe,Z∶=μI-C/4是可行的且在内部,其中μ是使得Z为正定矩阵的常数.

1.2 超平面舍入算法

计算最小化问题的上界通常利用启发式方法确定原问题的可行解.对于求得的模型(SDP)的最优解,主要利用Goemans等[7]对最大割问题提出的算法以及Frieze等[8]提出的改进的随机舍入算法,设计图二分的超平面舍入算法以得到问题(GPKC)的近似最优解,即图二分的初始划分.下面给出完整的图二分超平面舍入算法.

算法1图二分的超平面舍入算法.

输入: 模型(SDP)的最优解Y,目标矩阵C,顶点权重向量B,资源上限U,抽样次数p;

初始化:x=[ ],f=[ ];

步骤1) 对Y做Cholesky分解DTD=Y得到D;

步骤2) fort=1,2,…,p

步骤3) 取单位球面Sn上服从均匀分布的单位向量st;

步骤5) end

步骤6) 取min(f)对应的x赋值于y,并令err=max{(y+e)TB-2u1,0}+max{(e-y)TB-2u2,0};

步骤7) if ∃ err=0

步骤8) 输出对应的y;

步骤9) else

步骤11) 令err=max{(x+e)TB-2u1,0}+max{(e-x)TB-2u2,0};

步骤12) if ∃err1=0

步骤13) 若∃err=0,则输出min(f)和min(f1)对应的[x,y1];

步骤14) else

步骤15) 若∃err=0,输出min(f)对应的x; 反之,对x做一邻域调整得x1,计算相应的f和err值;

步骤16) 若∃err=0,输出min(f)对应的x1; 反之,输出调整后min(f)和min(err)值对应的[x1,y1];

步骤17) end

步骤18) end

输出: 目标值最优的划分.

算法1中步骤10)的邻域调整是指: 令P1={i|y(i)=1},P2={i|y(i)=-1},将P1中单点逐次移动到P2,再将P2中单点逐次移动到P1,得到相应的y1.

1.3 均衡因子

在对问题(2)中目标函数值进行极小化时,由于在实际问题中常将ωij视为非负数,因此当xi和xj均为1或均为-1,即顶点全划分在同一个集合时,可得最小目标值0,与本文划分思想不符.为避免上述情形发生,同时减少划分导致的资源浪费,本文考虑在目标函数中添加一个均衡因子,用于控制划分结果的均衡性.用顶点权重向量B除以顶点权重的最大值,得列向量β,进一步可得矩阵A=ββT,此时由模型(SDP)可得新的目标矩阵C=C+aA,其中a是均衡因子,本文令a=300.

1.4 二分图的启发式算法

二分图启发式算法可用于提高各种组合问题的解决方案质量[20].在利用超平面舍入算法得到初始划分后,本文用该方法进一步改进划分的质量,下面给出改进的二分图启发式算法.给定划分结果(P1,P2),在满足容量限制的条件下,寻找使目标函数值更小的划分结果.

算法2图划分问题的启发式算法.

输入: 划分组合(P1,P2),目标值f*,目标矩阵C,划分矩阵R,停止误差ε;

初始化:δ=0;

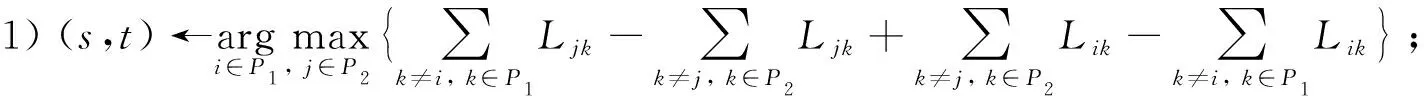
步骤3) whileΔcost>ε

步骤4)P1←P1-{s}+{t},P2←P2-{t}+{s};

步骤7) end

步骤8) fort=1∶length(Pi),其中i∈{1,2},j∈{1,2}i

步骤9)r←Pi(t),令Pi←Pi-{r},Pj←Pj+{r};

步骤10)H=CR,δ1=C(r,r)-H(r,i)+H(r,j);

步骤11) ifδ1<δ

步骤13) end

步骤14) end

2 图的多分问题

图的多分问题是将图的顶点集划分为多个集合,使得各划分集合在顶点权重不超过资源上限的情形下,连接不同子集的边的总权值最小化.由于所建模型有多个约束条件,而内点算法又因内存问题无法求解大规模实例,因此针对图的多分问题,本文利用改进的图二分算法设计递归二分的图多分算法.

在图二划分不可行的情形下,需额外增加资源满足图二分的可行性.为避免后续划分时因资源不足而导致划分结果不可行的情况,本文引进缩小资源的参数m,利用增加资源后新资源的m倍进行划分,令m=0.7.从而在保证二分可行的同时,避免出现资源不足的情况.下面给出增加资源的全过程.

算法3资源变更算法.

输入: 前两块资源二分的结果x*,资源上限U,剩余的资源块φ,缩小资源参数m;

步骤1) 判断x*的可行性,即顶点权重是否满足资源约束,将不可行的块记入ψ;

步骤2) whileψ非空

步骤3) whileφ非空&ψ非空

步骤4)uψ(1)=m[uψ(1)+uφ(1)],φ(1)=[ ],ψ(1)=[ ];

步骤5) end

步骤8) end

步骤9) 当资源增加使得二分可行时,将增加资源后的大块及其对应的顶点按相应的初始资源大小继续二分,直至得到最后的划分结果P;

输出: 划分结果P.

算法4递归二划分求解图多分问题.

步骤1) 建立模型(GPKC),利用内点法求解半定规划松弛模型(SDP),对模型(SDP)最优解Y用超平面舍入算法(算法1)得到图二分的初始划分;

步骤2) 若二分不可行,则转步骤3);

步骤3) 利用算法3对不可行的划分集合增加划分资源,直至二分可行,再将增加资源后的二划分集合继续进行二分,最后得到图的k划分结果;

步骤4) 利用图的启发式算法(算法2)对图的k划分中每两个划分集合的顶点进行调整,以得到使目标函数值更小的划分;

步骤5) 合并未充分利用资源的集合.

3 数值模拟

下面用MATLAB R2021b实现本文算法,数据来源于文献[15]中部分随机生成图数据以及文献[13]中生成的大规模数据,其中(GPKCrand20),(GPKCrand50),(GPKCrand80)分别表示邻接矩阵中非零边权值占比20%,50%,80%的图.将利用递归二划分算法求得的最小切边权值与文献[15]中对GPKC问题DNN松弛模型所设计的Vc+2opt算法求得的切边权值进行比较,并用gap表示两者切边权值之间的差距,其中gap=(递归二划分算法所得目标函数值-(Vc+2opt算法所得目标函数值))/(Vc+2opt算法所得目标函数值).为保证实验结果的合理性,本文对每个测试样例均进行10次实验,取实验最好结果及平均的CPU时间,结果列于表1.

表1 递归二划分算法与Vc+2opt算法的实验结果

表1给出了递归二划分算法和Vc+2opt算法对500和1 173个顶点的划分结果以及各算法所花费的CPU时间.由表1可见: 递归二划分算法随着容量上限的减少,划分所需时间逐渐增加; 由于本文提出的递归二划分算法是在考虑去掉顶点权重约束的情形下求解半定规划松弛模型,大幅度减小了求解模型的次数,且计算过程中迭代次数较少,从而在较短的时间内可得到递归二划分算法的较优解.此外,由两种算法所得函数值的差距gap可知: 当gap为正,即递归二划分算法所得目标函数值比Vc+2opt算法所得函数值大时,递归二划分算法可在较短时间内得到与Vc+2opt算法函数值差距最大为1.19%的较优目标函数值; 当gap为负时,表示递归二划分算法的函数值优于Vc+2opt算法所得目标函数值,且两者所得目标函数值差距最多为5.87%.

综上所述,本文针对带有顶点权重约束的图多分问题,设计了递归的二划分算法.首先,考虑用内点法求解不加顶点权重约束的半定规划松弛模型; 其次,通过随机扰动得到满足顶点权重约束的可行解; 最后,利用启发式算法,对可行解进行局部改进得到更紧的上界.同时加入均衡因子以避免半定规划目标值为0以及因划分不均衡导致的资源浪费,并设计了求解后的划分合并算法.实验结果表明,本文提出的递归二划分算法可高效地求解带约束的图多分问题,得到了较优的划分结果.