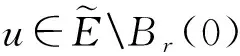具有变号位势Kirchhoff-Schrödinger-Poisson系统解的存在性
余 标,叶晓峰,杨 丹
(华东交通大学 理学院,南昌 330013)
1 引言与主要结果
考虑如下Kirchhoff-Schrödinger-Poisson系统:
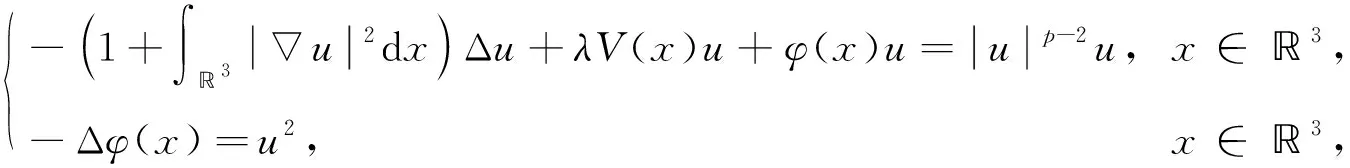
(1)
其中λ是一个正参数,p∈(4,6).系统(1)对应的能量泛函为
(u,φ)是系统(1)的解当且仅当其为Jλ(u,φ)临界点.
注意Poisson方程-Δφ(x)=u2在D1,2(3)中有唯一解利用文献[2-3]中的化简方法可知,要证明系统(1)存在弱解,只需证明能量泛函Iλ(u):H1(3)→存在临界点即可.Iλ(u)定义为
文献[4-10]研究了Schrödinger-Poisson系统各种解的存在性,但在变号位势情形下对该问题的研究较少.对于变号位势的问题,由于V在某些地方为负,因此能量泛函I将不再满足一般的环绕定理.文献[11]利用Morse理论得到了Schrödinger-Poisson系统非平凡解的存在性.本文在文献[12-13]的基础上,利用变分法给出系统(1)具有无穷多个不同的非平凡解.
对位势函数V做如下假设:
(H1)V∈C(3,),且V下有界;
(H2) 存在一个常数c>0,使得集合{x∈3:V(x)≤c}非空且meas{x∈3:V(x)≤c}<+∞,其中meas表示3中的Lebesgue测度.
本文的主要结果如下:
定理1假设(H1)和(H2)成立,且4 设H1(3)={u∈L2(3):u∈L2(3)}是一般的Sobolev空间,具有如下标准内积和范数: 定义本文的工作空间为 具有如下内积和范数: 其中V±(x)=max{±V(x),0},且V(x)=V+(x)-V-(x).由文献[12]可知,Eλ嵌入到Ls(3)是连续的,其中2≤s≤6.因此,存在一个常数as>0,使得 ‖u‖s≤as‖u‖λ, ∀u∈Eλ, 其中‖·‖s表示Ls(3)中的范数.根据文献[13],假设 Fλ={u∈Eλ: suppu⊂V-1([0,+∞))}, (2) 命题1[13]设(H1),(H2)和V-≠0成立,则对任何固定的j,有: 1) 当λ→+∞时,μj(λ)→0; 2)μj(λ)关于λ是一个不增的连续函数,其中 设 命题2[14]设E是一个无穷维的Banach空间,I∈C1(E,)是偶泛函,满足(PS)(Palais-Smale)条件及I(0)=0.如果E=V⊕X,其中V是有穷维的,且I满足如下条件: 1) 存在常数ρ,α>0,使得I|∂Bρ∩X≥α; 则I有一个无界的临界值序列. 为研究泛函Iλ,本文将利用涉及φu项的以下性质: 命题3[15]存在常数a1>0,使得对所有u∈H1(3)均有 引理1设(H1)和(H2)成立且4 证明: 由于在有穷维空间中所有的范数都等价,故存在常数Cp,C>0,使得 ‖u‖D1,2(3)≤C‖u‖λ, 由于p∈(4,6),故只需取r充分大,即知结论成立. 引理3设(H1)和(H2)成立且4 显然矛盾. 如果w≠0,则集合Ω={x∈3:w(x)≠0}有正的Lebesgue测度.对于x∈Ω,一方面,当n→+∞时有|un|→+∞; 另一方面,根据法图引理可知,当n→+∞时因此,根据命题3可知, 显然矛盾.因此{un}在Eλ中有界,不妨设‖un‖λ≤T,必要时取子列,则存在u∈Eλ和A∈,使得在Eλ中un弱收敛到根据可知 设vn∶=un-u.由(H1)和(H2)可知 因此, 令Λ>0充分大,则当λ>Λ时在Eλ中有un→u,结论成立.2 预备知识
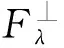



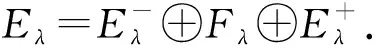
3 主要结果的证明