带p(t)-Laplace算子的分数阶Langevin方程参数型反周期边值问题解的存在性

倪晋波,陈 港,董蝴蝶

(安徽理工大学 数学与大数据学院,安徽 淮南 232001)

0 引 言

分数阶微分方程广泛应用于光学、热学系统、数学建模和力学等领域[1-3].Langevin在研究粒子布朗运动时,导出如下方程[4]

(1)

式(1)称为Langevin方程.在复杂介质环境下,方程(1)不能准确描述物体运动的动力学行为.基于分数阶微分算子的长程相关性和记忆性,Lutz[5]和Burov 等[6]提出了下列分数阶Langevin方程:

目前,关于分数阶Langevin方程(初)边值问题解的存在性研究已被广泛关注[7-13].例如,Ahmada等[9]利用Krasnoselskii不动点定理讨论了如下Langevin方程三点边值问题解的存在性:

(2)

(3)

(4)

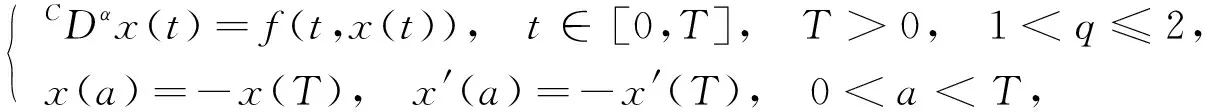
(5)

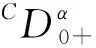
受上述研究结果的启发,本文讨论带p(t)-Laplace算子的分数阶Langevin方程参数型反周期边值问题:

(6)

1 预备知识

定义1[3]函数f: (0,+∞)→的α(α>0)阶Riemann-Liouville型分数阶积分定义为

其中等式右端在(0,+∞)上有定义.

定义2[3]函数f: (0,+∞)→的α(α>0)阶Caputo型分数阶导数定义为

其中n=[α]+1,假设等式右端在(0,+∞)上有定义.

定义3[15-16]对任意的(t,x)∈[0,1]×,φp(t)(x)=x是从到的同胚映射,且当t固定时,φp(t)(·)是严格单调递增的,其逆映射定义为

是将有界集映成有界集的连续映射.

引理1[3]令α>0,假设f∈ACn[0,1],则

(7)

其中ci∈,i=0,1,2…,n-1,n=[α]+1.

引理2(Schaefer不动点定理)[17]设X是Banach空间,算子T:X→X为全连续算子,若集合Ω={x∈X|x=μTx,μ∈(0,1)}有界,则算子T在X中至少存在一个不动点.

2 主要结果

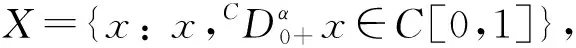
引理3分数阶Langevin方程

(8)

在边值条件

(9)

下,有如下形式的解:

其中

(10)

由边值条件(9),可得

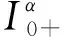
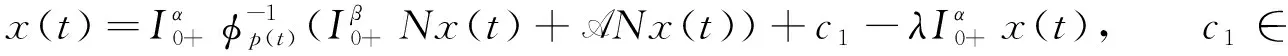
(11)

利用边值条件x(a)=-x(1),可得

将式(12)代入式(11)即证得结论.

基于引理3,定义算子T:C[0,1]→C[0,1]如下:

从而边值问题(6)解的存在性等价转化为证明算子T存在不动点.

定理1设f: [0,1]×2→连续,且满足条件: 存在非负函数ξ,φ,η∈C[0,1],使得

(13)

则当

(14)

时,边值问题(6)在X上至少有一个解,其中

l∶=max{(‖φ‖∞+‖η‖∞)1/(pm-1),(‖φ‖∞+‖η‖∞)1/(pM-1)}.

证明: 证明分两步完成.

于是有

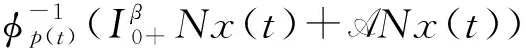
2) 证明算子T在X上存在不动点.定义集合S={x∈X|x=μTx,μ∈(0,1)}.根据Schaefer不动点定理,证明算子T在X上存在不动点只需证明S有界.对任意的x(t)∈S,由条件式(13)可得

从而有

由不等式(u+v)q≤2q(uq+vq)(u,v,q>0)和xr≤x+1(r∈[0,1],x≥0)可知,对任意的t∈[0,1],有

因此,

结合式(15),(16)可得

由条件式(14)和式(17)可推出存在一个常数G>0,使得‖x‖X≤G.由Schaefer不动点定理可知,T在S中至少存在一个不动点,即边值问题(6) 至少有一个解.

3 应用实例

例1考虑边值问题

(18)

由定理1可知边值问题(18)至少有一个解.