基于核心素养的高中数学深度学习探析

马艳波

（延边州教育学院，吉林 延吉 133000）

随着经济、科技的迅猛发展和社会生活的变化，教学改革也发生重大的变化。把提高学生综合素质、着力发展学生的核心素养作为育人目标。教育的目的是培养全面而又个性的社会主义建设者和接班人，更多地强调“人”的全方位的发展。育人目标的变化必然会使得学校、教师的教育方法发生变化，教师需要转变教育观念，改变教学方法，思考怎么教才能更好地达成育人目标。应运而生出现了深度教学和深度学习。而学生的深度学习一定建立在教师的深度教学和引导之下，深度教学一定建立在教师的深度学习、深入研究的基础之上。所以，教师要深刻理解并践行深度学习。

深度学习是理解性、融入性的学习。学习者能够批判性地将学习的新知识纳入已有的认知结构中，并能将众多的信息进行比对，遇到新问题、新情境能将知识进行迁移，作出决策和判断。这种学习是深刻的，长久的，新知识与原有的知识融合，成为学习者知识体系的一部分，变成学习者的能力和用来解决问题的工具。与深度学习相对的浅层学习则是表象的记忆性学习。对于众多的新的信息，学习者将他们作为孤立的，不相关的事实来记忆，不会归类，不会查找与已有知识间的联系。由于信息的孤立性，记忆起来就会感到多且杂，不能形成网，不成体系，不能运用自如，正是由于这种情况，造成学习的表面性，记忆的短时性，不能对知识和信息的理解保持长期性，所以我们要进行深度学习。

数学作为研究数量关系和空间形式的基础学科，它的抽象性，逻辑性对人的思维的培养、对思维灵活性的训练极其重要，具有不可替代的作用。正是数学学科的特殊性决定了数学的深度学习势在必行。数学的抽象经历两个阶段：一是基于现实的抽象，二是基于逻辑的抽象。基于现实的抽象有些有实际意义，有些并没有实际意义，例如数字1、2、3，它本身没有实际意义，但这些抽象出来的东西是存在的，它存在于人们的头脑中，并被人们普遍认识。正是由于这种抽象的存在，人们对现实世界的认识才能从感性上升到理性，才可以在这些符号、概念的基础上，进行第二阶段的抽象，将上一阶段的抽象进行逻辑化，将知识符号化、公理化、形式化，这个阶段是从理性到理性的思维过程。我们高中数学学习就是训练学生用学到的概念、定理、公理、数学语言（数学符号）来描述世界，学生需要记住并理解符号的意义，并用它们解决问题，这种学会并将之扩大延伸的学习，就是将知识内化为能力的学习，就是深度学习。

数学深度学习，不仅依赖数学知识，数学语言，还依赖数学的解题思想。教师要熟练掌握教学内容和教学方法，在教学的过程中逐步将这些知识、思想、方法教给学生，只有这样才能使知识得以延续，学生的思维得到发展，这也是数学教师应该具备的思维品质。高中数学教学内容很多，其核心内容突出函数、几何与代数、概率与统计、数学建模活动与数学探究活动这四条主线。这四条主线贯穿必修，选择性必修和选修的整个教程。教师要深入研究每条主线的知识结构，教学内容以及通性通法。

为此，数学深度学习必须在原有的认知结构的基础上依托教学内容、学科思想与方法，对问题进行深入思考和系统化整合。从内容层面讲，数学深度学习是以建构学科结构体系为目的的学习，以学科知识为核心，思想方法为依托，整合、提炼学科本质的学习；从思维层面讲，数学深度学习是以提升学习品质为目的的学习，由具体的思想方法与策略过渡到一般性思维与策略的学习；从过程层面讲，数学深度学习是培养数学核心素养的学习，始终关注学生身心健康成长过程的学习。下面以几个具体实例说明怎样在教学中进行深度学习。

一、多角度思考，注重知识间的横向联系，发展学生的数学思维

例1.正实数a,b满足a+b=2，求a2+b2的最小值。

这个看似简单的问题，它其实有多种求解方法，每一种求解方法都能很好地发展学生的数学思维，提升学生的数学核心素养。但由于思维的局限性，对于这道题，教师在教学过程中往往只采用代数方法进行证明，对于几何法和向量法用得很少，甚至有些教师根本就想不到用这些方法解决问题。为此，教师在教学过程中的引领地位是非常重要的，教师的思维高度、思考问题的广度决定了他所教学生思维的高度与广度。所以，教师不仅要全面理解教材、掌握教法，更要多学，多看，多想，对出现的问题一定要全方位，多角度考量，只有教师的思路开阔了，思维灵活了，才能将核心素养落到实处。

1.公式法

（1）基本不等式法

解析：因为基本不等式学生很熟悉，所以，对于本题，学生很容易想到用基本不等式去解。思考学过的内容，建立a2+b2与a2+b2的关系式。

（2）柯西不等式法

解析：柯西不等式是常用的求解最值的公式，其特点是左右两侧都为二次式。方法非常简单，只要学生掌握其形式特征，掌握等号成立的条件，类似填空一样，把所求的内容填上即可求得最值。

方法2：由(a2+b2)(1+1) ≥ (a+b)2可得。

2.函数法

解析：一般来说，最值问题大多是函数最值问题，很少有直接用公式可以求解的。所以，函数法是学生必须掌握的求解方法。函数只能有一个变量，从已知条件出发，思考将谁作为变量，将谁作为参数，问题转化成含有一个变量的函数，用函数方法来求最值。

解：由a+b=2，可得b=2-a＞ 0所以a2+b2=a2+(2-a)2=2a2-4a+4=2(a-1)2+2可得。

3.几何法

本题教师可以引导学生从横向、纵向进行深挖，从代数、几何、向量法三个方向探究，分别应用公式法、函数法、数形结合法、几何法、向量法求解，以此开阔学生的视野，发展学生的数学思维。通过讲解，使学生对所学的知识有了更深的认识，拉近了知识的横向联系，打开学生的解题的思维固式，活学活用，提高学生的学习兴趣，开阔解题思路，对学生的学习起到积极作用。当然，这对教师的知识储备和教学能力有较高的要求。

二、一题多解，纵向深挖学科知识，丰富学生的解题思路

例2.如图1，四棱锥P-ABCD，底面ABCD 是正方形，PD⊥底面ABCD，PD=，AD=1，E、F 分别是AB、PC 的中点，求证：EF//平面PAD。

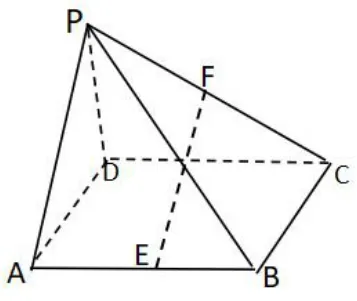
图1

这道证明线面平行的问题很简单，解题方法也有多种。学生更容易想到利用线线、线面、面面关系推理证明：一是利用线线平行证明线面平行；二是利用面面平行证明线面平行。这也是最常用的方法，是学生必须掌握的方法。而本题还可以用向量法和割补法，所以，教师应该深入挖掘题目所给的条件，从中找到可利用的信息。

1.由线线平行推证线面平行

解析：题中给出线段的中点，学生很容易想到利用三角形中位线的性质求解。本题的中位线的选取有两种：一是在图形内部，根据已知条件，作出三角形中位线；二是在图形外部作图，将边的一部分作为中位线，利用中位线的性质推理证明。

方法1：（图2）取PD 中点H，连接AH、FH易得四边形AEFH 为平行四边形。

（图2）

方法2：（图3）连接并延长CE，与DA 的延长线交于H，连接PH，只需证明A 为DH 中点即可；利用线线平行可得线面平行。

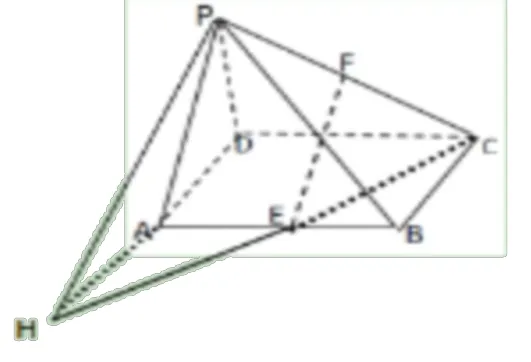
（图3）

2.由面面平行推证线面平行

解析：利用面面平行推得线面平行也是常用的方法。本题的关键是找到EF 所在的平面。根据题中所给的条件，利用中点，找中位线，学生容易找到以下两种平面，用两相交直线平行于一个平面，则两平面平行，进而通过面面平行证明线面平行。

方法3：（图4）取DC 中点H，利用中位线性质可得面EFH//面PAD，由面面平行，证得线面平行。

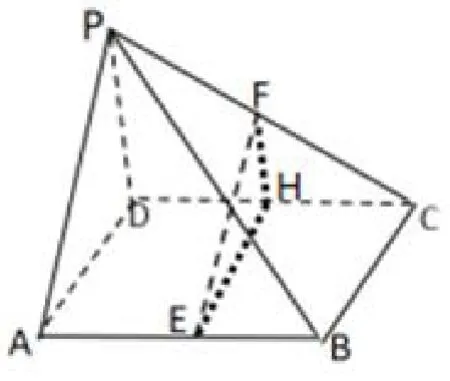
（图4）

方法4：（图5）取PB 中点H，利用中位线性质可得面EFH//面PAD，由面面平行，证得线面平行。

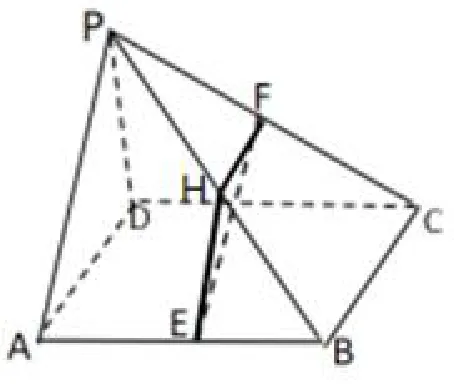
（图5）

3.空间向量法和割补法

解析：由于交于一点的三条直线两两垂直，所以，考虑用向量法求解；也可以将图形放到长方体中进行讨论。长方体作为特殊几何体，对于长方体内的线面，线线、面面或者成角问题，学生很熟悉。这样做会使问题的难度降低，学生更容易得到结果。

方法5：建立空间坐标系，只需证明EF 与面PAD 的法向量垂直即可。

方法6：将图形放到长方体中求解。

教师还可以将问题扩展开。

（3）若PD 不垂直于底面又怎么求解？

如此一来，随着问题的变化，学生对这道题的研究越来越深入，学生的思维得到训练，知识掌握得更加扎实，对此类问题的解法有更系统的了解，以后遇到这类问题就有了大致的解题思路了。如此经过长期的学习，学生的解题能力会得到大幅度的提升。

三、一题多变，培养学生的解题能力，发展数学学科素养

例3.已知函数f(x)=2x-x-1，则不等式f(x) ＞ 0的解集是（ ）

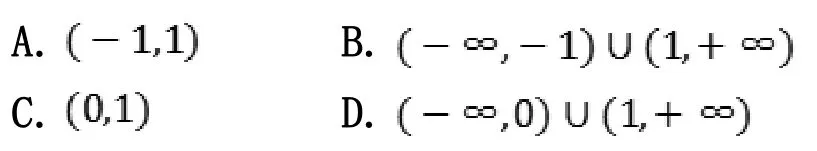
解析：此类题不可能直接求解，本题重点是让学生掌握一类问题的解法：数形结合法。数形结合法中，“数”与“形”都非常重要，它直接影响解题难度，“数”要简单，“形”要易得。所以，函数的选择很重要，一定是我们熟悉且图像容易画出来的函数，本题把它看成y=2x-1与y=-x；或者看成y=2x与y=-x+1的交点问题，通过图像很容易得到结论。

教师提出问题：“能不能看成y=2x+x与y=1”的交点问题？为什么？以此引发学生探讨，激发学生的探究欲望。

本题还可以进行变式，变式本着由浅入深的原则，让学生的思维螺旋式上升，以此来加深学生对知识的理解，提升学生的学科素养。

1.变成等式

变式1.讨论函数f(x)=的零点个数。

解析：在同一个坐标系内画出y=和y=k图像。本题变式后的难度在于指数函数的有界性，函数y=2x值域是(0,+∞)，所以，y=2x-1的值域是(-1,+∞)，故y=在x＜ 0部分图像在x=0和x=1之间，且在x=1下方。移动平行于x 轴的直线y=k，通过图像观察即可。

2.变换函数

变式2.若对任意的x，不等式e x-x-k＞ 0恒成立，求k 的取值范围。

解析：类比上题，题目看起来难度大了很多，将2x换成ex，y=-x+1 换成y=x+k，比原来的题多了一个参数。但解法是一样的，只需将题转化为e x＞x+k，在同一坐标系内画出y=ex和直线y=x,平移y=x，寻找y=ex与y=x+k 的切点。

3.变换角度

变式3.对于任意的x1、x2，求的最小值。

解析：这个问题难度更大，学生对此类问题如果没有经过训练，恐怕很难求解。一道题中出现两个变量，如果用代数法去解，那么，谁为变量，谁为参数？所以，它不是学生常见的代数问题，通过观察发现，它是根式形式，且根号下是平方形式，这类问题可以从两点间距离的角度求解。哪两个点？通过x1、x2的位置，找到两个函数y=ex和y=x。本题看成y=ex上的点(x1,)到直线y=x的点(x2,x2)距离的最小值。问题就转变为变式2了。可以通过平移直线，找到切点，用距离公式求解即可。

一题多变，一题多解是数学教学的重要手段，是实现深度学习，培养学生数学思维，落实数学核心素养的重要途径。要想在教学过程中能更好地变式，教师要自己站得高，从总体上把握教材，了解教法，并不断地学习、积累，探究，只有这样才能使学生的思维得到长足发展。

总之，教育的目的是实现“人的发展”，实现人类历史文化的传承。教师在教学过程中要深入探讨教学规律，研究学习规律，合理设计教学内容，多方位，多角度思考问题，最大化地为学生的发展提供帮助，调动学生的积极性、激发学生的学习兴趣，让学生学会运用学科知识去解决问题，去理解世界，学以致用。与此同时，让学生健康快乐地成长，获得健全的人格和强健的体魄，成为符合新时代要求的社会主义建设者和接班人。