多无人机辅助移动边缘计算中的轨迹优化

江 雪,赵 亮

(1.南京邮电大学 物联网学院,江苏 南京 210003;2.杭州昊舜视讯科技有限公司,浙江 杭州 311100)

0 引 言

随着信息相关技术的飞速发展,智能化的应用越来越普及,大量密集的计算任务使得移动终端的带电量和计算能力都无法满足人们日益增长的需求。移动边缘计算(mobile edge computing,MEC)[1-2]应运而生,它通过将计算任务卸载到边缘服务器,可以有效地提高终端设备电池的使用寿命,降低整个网络的时延。另外一方面,无人机[3](unmanned aerial vehicle,UAV)由于其灵活性高、机动性强、成本低、可靠性高、操作简单等优点,被广泛应用于边缘计算网络中。即使是在地理位置复杂的区域,无人机也可以实现高效快速的部署,较好地解决应急通信的需要。目前关于无人机应用于移动边缘计算的研究主要集中在以下三个方面:一是无人机作为空中数据中继[4-6],为远距离的用户提供可靠的无线连接。二是无人机作为飞行的无线接入点,用于物联网中用户设备的数据收集与分发[7]。三是无人机作为移动基站通信[8],可以为蜂窝网络提供有效补充。不论是无人机的哪种应用,无人机的飞行轨迹都会直接影响边缘计算网络的能耗、时延和计算效率等关键性能,因此,无人机的轨迹问题研究是近几年学术界和工业界研究的热点。

目前无人机辅助移动边缘计算网络中针对无人机飞行轨迹优化算法的研究大部分都集中在以能耗最小化为目标。文献[9]在满足用户服务需求的限制条件下,联合优化用户发送功率、计算卸载策略等设计基于能耗最小化的无人机轨迹优化算法。文献[10]在满足无人机飞行速度的限制条件下,通过最大最小化地面设备可收集能量,设计无人机的最优飞行轨迹。文献[11]考虑用户和无人机之间的上行和下行通信链路,在正交和非正交接入的两种模式下,以加权最小化无人机和设备的能耗为目标,联合设计计算资源分配策略和无人机最优轨迹。文献[12]通过强化学习和分簇的方法设计基于能耗最小化的无人机轨迹优化算法。文献[13]在满足用户服务需求的条件下,最大化能量效率,即最大化卸载总数据量比总能耗,联合优化无人机的飞行轨迹、用户的发送功率和计算卸载策略。文献[14]通过辛普森法和遗传算法求解基于能耗最小化的无人机轨迹优化算法。文献[15]通过加权方式最小化无人机能耗和地面设备能耗,优化资源分配策略和无人机飞行轨迹。文献[16]在满足设备服务质量要求和可用计算资源的条件下,联合优化任务卸载策略、资源分配策略以及无人机的飞行时间,提出基于无人机飞行能耗和计算能耗最小化的轨迹优化算法。上述大部分无人机辅助边缘计算网络的研究都是针对网络中只有一架无人机优化其轨迹路径提高网络整体性能,而实际的移动边缘计算网络中,情况复杂,许多情况下需要多架无人机协同[17-18]工作完成任务,提高工作效率和优化网络整体性能。基于此,该文主要以能耗最小化为目标,在满足无人机机械特性的条件下,同时考虑多架无人机之间需满足防碰撞的约束条件,协同优化多架无人机的飞行轨迹。

1 系统模型

考虑多架无人机辅助的移动边缘计算网络,网络中有K(k=1,2,…,K)架无人机为U(u=1,2,…,U)个地面设备提供服务,每个地面设备卸载部分任务给某架无人机,本地执行剩余任务。此外,每个地面设备只能卸载任务给某一架无人机,每架无人机可以接收多个地面设备的卸载任务,如图1所示。

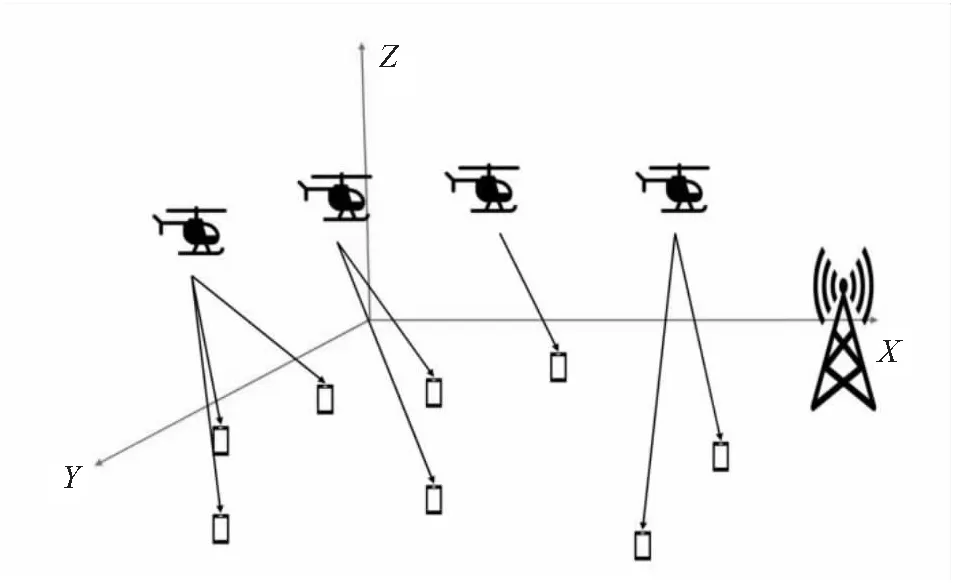
图1 多无人机辅助移动边缘计算网络模型

每架无人机已知所有在水平地面设备的笛卡尔位置坐标。其中,第u个设备的位置可以表示为:

Ou=[xu,yu]T,u=1,2,…,U

(1)

另外一方面,无人机在固定高度H的平面飞行,其飞行的时间周期为Tf秒,Tf秒被划分为T个等长时隙,其位置可以表示为:

ck(t)=[xk(t),yk(t),H]T,0≤t≤T

(2)

该文主要考虑视距(line of sight,LoS)信道和非视距(non-line-of-sight,NLoS)信道[17]。在时隙t,第k架UAV和第u个地面设备在LoS信道的连通概率可以表示为:

(3)

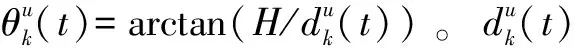
(4)

进一步可得,在时隙t,第k架无人机与第u个地面设备之间的路径损耗系数[17]为:

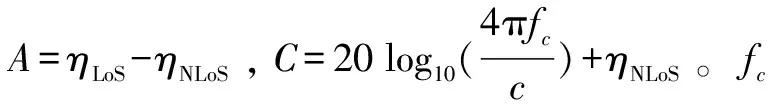
第k架无人机和第u个地面设备在时隙t的信道功率增益[17]可以表示为:

(6)

由于LoS链路的中断概率比NLoS链路高很多,在时隙t,第u个地面设备向第k架无人机卸载任务时的数据率可以表示为:

(7)

1.1 通信模型

(8)

(9)

1.2 无人机模型

该文假设每架无人机在每个时隙的速度为恒定值vk(t),无人机的速度受到最大速度Vmax的约束,需满足如下约束条件:

(10)

其中,δ=Tf/T表示每个时隙的长度。

为了确保所有无人机可以为地面设备提供稳定可靠的服务,假设每架无人机飞行一个时间周期Tf后都需要回到最初的位置充电,即需要满足:

ck(1)=ck(T)

(11)

另外一方面,多架无人机在同一水平面飞行执行任务,每架无人机之间还需要保持一个最小安全飞行距离dmin以避免发生碰撞,因此需满足:

‖ci(t)-cj(t)‖≥dmin,∀i,j=1,2,…,K;i≠j

(12)

无人机飞行需要消耗的能量主要与其重量和飞行距离有关。因此在每个时隙,无人机的飞行能耗[9]可以表示为:

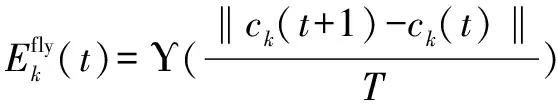
(13)

其中,Υ表示无人机的有效载荷。

2 优化问题建模

无人机辅助边缘计算网络中,无人机的能耗远大于地面设备的能耗,无人机的能耗[15]主要由以下几个部分组成:与地面设备之间通信的能耗、接收地面设备卸载任务的能耗、执行接收卸载任务的计算能耗和飞行能耗。其中,接收地面设备卸载任务的能耗和飞行能耗受到无人机飞行轨迹的影响最大,因此主要考虑接收卸载计算任务的能耗和飞行能耗。根据上述分析,可以建立如下优化问题:

(14)

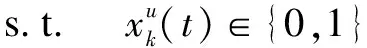
(a)

(b)

ck(1)=ck(T)

(c)

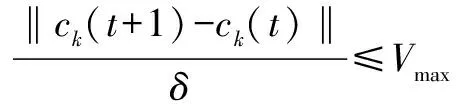
(d)

‖ci(t)-cj(t)‖≥dmin,∀i≠j

(e)

优化问题(14)中的式(a)和(b)对应地面设备和无人机之间的卸载决策参数值的约束条件。(c)、(d)和(e)对应无人机飞行轨迹的约束条件。

3 优化问题求解

可以看出,由于优化问题(14)为非线性的优化问题,同时其对应的约束条件非凸,所以该优化问题很难求解。基于文献[9]中的交替最小化算法,将优化问题(14)拆分为2个子优化问题:(1)给定k架无人机飞行轨迹的条件下求解卸载决策参数的问题;(2)给定卸载决策参数的条件下求解多无人机的最优飞行轨迹的问题。

3.1 卸载决策参数求解

(15)

(16)

优化问题(14)可以转化为如下等价形式:

(17)

另外一方面,约束条件(a)和(b)可以转化为:

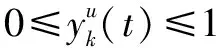
(18)

(19)

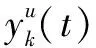
3.2 多无人机飞行轨迹求解

(20)

求解K架无人机的最优飞行轨迹,对应的约束条件为(c)、(d)和(e)。其中,约束条件(e)非凸,导致优化问题(20)无法求解,基于文献[20],采用连续凸优化 (successive convex optimization, SCA)的方法转化约束条件(e),因此对于任意给定的(ci(t))n和(cj(t))n的一阶泰勒展开式[20],有如下不等式成立:

‖ci(t)-cj(t)‖2≥-‖(ci(t))n-(cj(t))n‖2+

2((ci(t))n-(cj(t))n)T((ci(t))-(cj(t)))

(21)

其中,n为迭代步数。

根据上述分析,约束条件(e)可以转化为:

(dmin)2≤-‖(ci(t))n-(cj(t))n‖2+

2((ci(t))n-(cj(t))n)T((ci(t))-

(cj(t)))

(22)

即:

((ci(t))n-(cj(t))n)T((ci(t))-(cj(t)))≥

(dmin)2+‖(ci(t))n-(cj(t))n‖2

(23)

另外一方面,为了简化求解过程,由优化问题(20)可以看,第k架无人机在时隙t的坐标位置只与它前一个时隙t-1的位置有关,可以将优化问题(20)分解为T-1个子优化问题求解,逐步求解{c1(1)…ck(1)},{c1(2)…ck(2)},…,{c1(T-1)…ck(T-1)},对应需求解的子优化问题如下:

(24)

其中,t=1,2,…,T-1。

4 仿真结果及分析

在本节,通过MATLAB中的CVX来验算所提无人机轨迹优化算法的性能。考虑D×D的平面区域,K架无人机飞行在恒定的高度H=10 m,其中U个地面设备随机分布在区域内,并且所有无人机都已知所有地面设备的位置。实验中系统参数设置如表1所示。

表1 系统参数设置

续表1

实验主要考虑K=2和K=4两种情况分析UAV的飞行轨迹。当K=2时,2架UAV的起始位置分别为:(0,0)、(D,D)。当K=4时,4架UAV的起始位置分别为:(0,0)、(0,D)、(D,D)、(D,0)。

图2和图3分别展示了在网络中分别有2架和4架无人机时,不同数量地面设备条件下的无人机的飞行轨迹。由图可以看出,随着地面设备数量的增大,分布在区域中的范围变广,无人机的飞行距离也会相应变远,尽量地靠近设备,接收并完成卸载的任务。

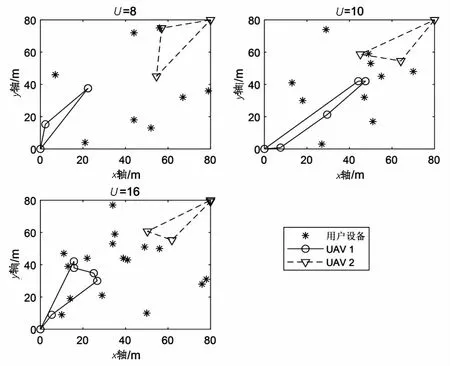
图2 K=2时,不同数量地面设备U={8,10,16} 对应的飞行轨迹

图3 K=4时,不同数量地面设备U={8,12,20} 对应的飞行轨迹

图4和图5分别展示了在网络中有2架和4架无人机时,不同无人机最大飞行速度约束下的无人机的飞行轨迹。由图可以看出,随着无人机最大飞行速度的上限值越来越大,无人机单步的可飞行距离越远,以便可以覆盖更广阔的区域。

图4 K=2时,不同无人机最大飞行速度V= {6,8,10}对应的飞行轨迹

图5 K=4时,不同无人机最大飞行速度V= {4,6,8}对应的飞行轨迹

图6和图7分别展示了在网络中有2架和4架无人机时,无人机在不同飞行时隙下的飞行轨迹。由图可以看出,随着无人机飞行时隙的增大,在总飞行周期时间固定的情况下,无人机的单步飞行距离在变短。

图6 K=2时,不同无人机飞行时隙T={5,8} 对应的飞行轨迹

图7 K=4时,不同无人机飞行时隙T={5,8} 对应的飞行轨迹

图8和图9分别展示了在网络中有2架和4架无人机时,不同能耗权重因子条件下无人机的飞行轨迹。由图可以看出,卸载能耗的加权因子越大,无人机越接近地面设备的位置。飞行能耗的权重因子越大,无人机的单步步长越小,这是由于UAV的飞行能耗主要和无人机飞行距离有关,而UAV的卸载能耗主要和无人机与设备之间的距离有关。

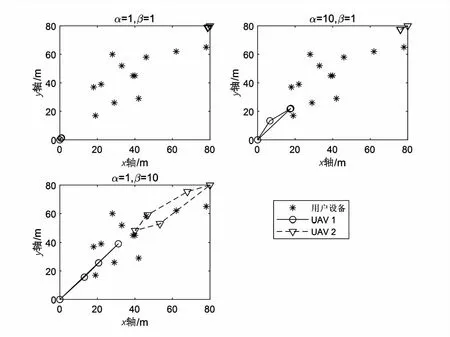
图8 K=2时,不同能耗权重因子对应的飞行轨迹

图9 K=4时,不同能耗权重因子对应的飞行轨迹

图10分别展示了在网络中有2架和4架无人机时,在不同能量权重因子的条件下无人机的飞行能耗和卸载能耗的关系。由图可以看出,随着无人机飞行能耗权重增加,无人机对应的飞行能耗有所增加。随着无人机卸载能耗的权重因子增加,无人机对应的卸载能耗有所增加。

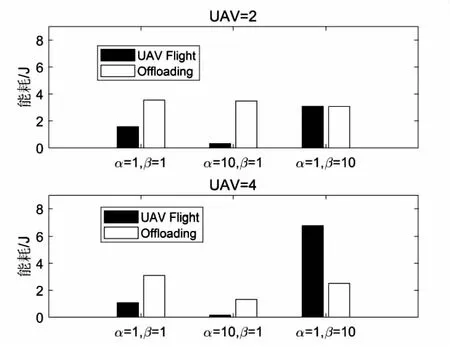
图10 不同权重因子对应的能耗关系

5 结束语

研究了多无人机辅助移动边缘计算系统,在满足无人机机械特性和多架无人机碰撞避免的条件下,以能耗最小化为目标,优化多无人机的飞行轨迹。为了解决非线性的优化问题和非凸的约束条件,引入辅助变量及转换优化问题为多个子优化问题求解。仿真结果验证了所提算法在得到多架无人机较优的飞行轨迹的同时,还明显改善了能耗。