基于正交化方法的页岩裂缝电特性仿真研究

郭 晨,雷阳艳*,凌博闻

(1.长安大学 信息工程学院,陕西 西安 710064;2.中国科学院 力学研究所,北京 100190)

0 引 言

在科学技术快速发展的背景下,计算机技术应用于各行各业,尤其在科研方面发挥极大的优势。近年来,随着人口数量及能源需求量的不断增长,急需开采出更多有价值的能源。页岩油气的巨大储量和成功案例,使其勘探开发技术成为研究的热点。然而实际的开采工作受环境、天气等各种因素限制,不能够实时快速获得实际储层数据。通过计算机仿真技术对实际情况进行理论建模,可以快速高效地解决实际工程中的复杂问题,也为实地勘探工作提供了理论依据[1]。

复杂的页岩裂缝网络在结构上具有随机性,其分布也存在多尺度特征[2-4],这为研究模型的建立带来一定挑战。2014年,Gale等人[5]通过对18种不同的岩样观察统计,得到了裂缝开度与特定开度裂缝在一定观测范围内出现的数量(即裂缝频数)之间的幂律关系。他们的研究结果表明,页岩中的裂缝网络普遍遵循这一幂律关系,不同页岩样本的区别体现在幂律参数上,这为建立符合页岩裂缝网络分布规律的模型提供了理论依据[6-7]。2018年,Han等人[8]通过计算机数值模拟和理论模型为模拟多孔岩石的介电特性提供了一种互补的方法。2019年,Han和Matthew等[9]进一步研究了定向裂缝在合成岩石中的等效介电特性,揭示了其在不同频率范围内发生的极化机制。2020年,刘婉萍等人[10]利用计算机仿真技术对页岩内部进行建模,得到了不同结构的页岩在其介电特性上呈现不同的规律,同时表明椭球内含物在不同方向呈现较强的各向异性。2021年,范珍珍等人[11]采用计算机模拟的方法提出使用二阶电学张量矩阵对裂缝模型的电各向异性进行分析。计算机模拟的运移和张量形式的电特性为研究裂缝网络非均一性提供了新的方法。

现有的预测储层电特性的理论模型大多基于均一介质假设,对非均一介质电特性的预测精度较低,因此很难应用于缝网密集储层的高精度反演。针对裂缝网络的特点,该文基于有限元仿真建模,使用了正交化方法,通过计算机平台设计了正交结构单元的相关参数,将裂缝网络在主方向的电特性映射到正交主裂缝和非均一性介质形成的简化正交结构上。通过该数值模拟实验设计的正交结构能够较好地还原原裂缝网络的电特性。

1 理论方法

1.1 裂缝宽度与尺寸分布关系理论

Gale等人[5]得到裂缝宽度b(毫米)与其对应的频数f之间的幂律关系:

f=Kbγ

(1)

在天然岩石裂缝构造中,裂缝的数量随着岩石裂缝宽度的增大而减小,故K值定量地描述了裂缝宽度与其对应数量的关系,Gale等人的工作中已经证实不同类型的岩石的K值不同。

1.2 各向异性介质的介电张量分析

电磁场媒质的本构方程可以表现为以下形式:

(2)

(3)

在计算介电常数的张量值过程中,对上式进行求逆,可得到:

(4)

1.3 传统理论模型与升尺度方法

1.3.1 Lorentz-Lorenz,Clausius-Mossotti (LLCM)

基于内含物分布的稀疏假设,Lorentz-Lorenz 和Clausius-Mossotti提出以下公式,用于计算两种成分的混合物的等效介电常数。

(5)

其中,ε1是内含物的介电常数,ε2是背景介质的介电常数,φ是孔隙度。

(6)

1.3.2 The Complex Refractive Index Method (CRIM)

复折射率法(CRIM)是假设混合物的复折射率是所有组分的复折射率的体积分数总和。根据这个原理,计算由水、岩石骨架组成的两相介质等效介电常数的CRIM公式如下:

(7)

其中,ε1是水的介电常数,ε2是岩石骨架的介电常数,φ是孔隙度。

1.3.3 升尺度方法

升尺度方法是一种将小尺度的实验观察数据或者参数转换为在大尺度下通过数值模拟得到新参数的方法。图1所示为页岩裂缝的升尺度过程,图1(b)是将图1(a)裂缝页岩模型网格剖分为4×4的网格模型,图1(c)将分割后的每一个小网格的裂缝模型升尺度为大尺度的方块网络模型。

图1 升尺度过程

1.4 数值模拟方法

目前常用于分析岩石物理特性的数值计算方法有有限差分方法[12](FDM)、有限元法[13](FEM)以及边界元法[14](BEM)等。由于页岩裂缝网络呈现较强的各向异性,结构复杂且不规则,对于网格剖分精度和速度有着较高要求,因此,该文选择了基于FEM方法的COMSOL Multiphysics®进行计算机建模与仿真分析[15]。COMSOL Multiphysics®多物理仿真软件是一种基于高级数值方法的软件,用于建模和模拟多物理场问题,具有强大的数据后处理能力。有限元法的实现需要三个阶段:前期处理阶段、计算求解阶段以及后期处理阶段。前期处理阶段是进行几何建模、材料的选择以及网格剖分;计算求解阶段是求解微分方程或微分方程组;后处理阶段是对所求的数据进行可视化以及误差分析,最后利用MATLAB软件进行数据处理。

2 正交化映射和正交结构设计

本实验首先通过电学特性(介电张量)将原复杂页岩模型映射到正交主裂缝上,保留了原有裂缝的连通性。如图2所示,在第一象限与第三象限添加了相同长径比的旋转椭球,来体现原有裂缝的各向异性。图2(a)、(b)、(c)为原裂缝网络的正交化过程,图2(a)、(d)、(e)为传统电特性升尺度模型。不同于电特性模型,在已知孔隙度的基础上,仅从理论公式上求解原裂缝模型的电特性,无法将裂缝网络的其他物性特征体现出来。该正交单元结构以电特性为依据,在保留连通性的基础上,也体现出了原裂缝的各向异性特征,同时简化了原复杂裂缝模型,大大提升了计算效率。

图2 裂缝网络的正交化与等效正交结构

图2(b)正交映射的两个垂直矩形的几何参数能够控制εxx和εyy两个介电参量值,使其与裂缝网络的介电参量值相等。图3(a)和(b)分别表示改变水平矩形的长度和宽度时,其两个介电参量的变化情况。从图中可以清晰地观察到:只有εxx介电参量值变化幅度较大,εyy变化幅度不明显。同理可以得到改变垂直矩形的长度和宽度可以控制εyy介电参量的变化,图4(a)和(b)分别表示改变垂直矩形框的长度和宽度时,其两个介电参量的变化情况。

图3 介电常数随水平矩形的几何参数的变化

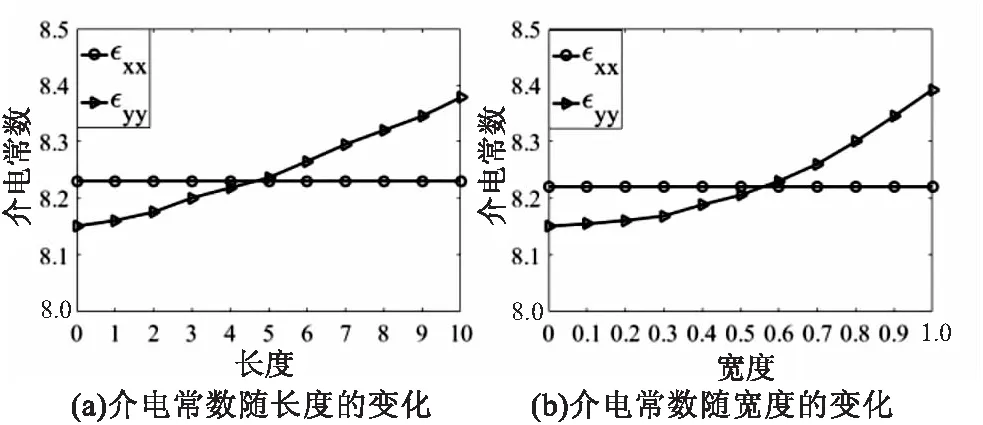
图4 介电常数随垂直矩形的几何参数的变化

由于椭球在不同电场方向上呈现不同的物理特性,因此为了保留原始自然裂缝的电各向异性特征,在正交结构中加入了具有较强各向异性的内含物(椭球)。图5(a)和(b)分别是随着第一象限和第三象限椭球旋转角度的变化,εxx和εyy介电参量的变化情况。通过改变图2(b)正交映射的不同几何参数使其与原复杂裂缝网络模型的介电参量值相等。由于介电常数表征一个介质的重要物理属性,不同的介质的介电常数值不同。可以根据第一象限和第三象限椭球的几何参量分别求出它们对应的介电常数矩阵,再将第一象限和第三象限的椭球等效为其介电常数矩阵对应的介质,这样便得到如图2(c)所示的正交结构单元。图5(a)和(b)分别是εxx和εyy两个介电参量的介电常数随椭球角度变化的情况。随着椭球旋转角度变化时,两个介电参量值都会有一个最大值和最小值。当第一象限和第三象限同时取最大值或最小值的介电参量矩阵时,代入图2(b)的正交映射中,便可以得到正交结构单元介电参量的取值范围。由于第二象限和第四象限的小圆球的半径比较小,对整体等效介电常数的影响很小可以忽略不计,因此可以将其等效为背景介质。

本工作基于正交化方法面向含裂缝页岩模型的电参数计算,将裂缝网络电特性映射到正交主裂缝和非均一性介质形成的正交结构上,如图2(a)、(b)、(c)所示。传统电特性模型(LLCM和CRIM经典理论公式)只能根据公式求解出其电参数值,然而无法精确地体现出页岩裂缝网络的裂缝形态以及连通性等物性特征,如图2(a)、(d)、(e)所示。该正交化方法在简化复杂缝网计算的同时,保留了裂缝网络原有的连通性。以裂缝网络的等效介电张量为依据,分别了定义了正交结构中主裂缝和基质的特性,并在此基础上在正交结构中加入各向异性内含物,体现原裂缝网络的各向异性特征,同时也能够获得正交结构等效介电特性的上下界,且上下边界能够包含原裂缝网络的电特性,为正交化方法的可行性提供了支撑,图5(a)、(b)为椭球旋转时可以得到介电常数的上下界范围。该方法也简化了原复杂裂缝模型,大大提升了计算效率。

图5 介电常数随椭球旋转角度的变化

3 计算机数值模拟实验

3.1 仿真模型建立及裂缝正交化

在实际勘探中,页岩网络裂缝分布错综复杂,受到沉积作用以及外力的挤压,形成了孔径与长度不一的天然裂缝。为了从电特性上系统地分析网络裂缝形态对模型电各向异性的影响规律,该文根据不同类型岩石幂律关系下的不同K值,通过COMSOL Multiphysics®计算机仿真软件模拟得到不同K值的裂缝网络模型。相关的实验硬件选取及实验设置:CPU处理器是Intel(R) Core(TM) i7-6700 CPU @ 3.40 GHz 3.41 GHz,64位操作系统;COMSOL Multiphysics®多物理场软件为COMSOL 5.6版本。在COMSOL Multiphysics®中创建二维几何结构,图6(a)、(b)、(c)分别表示K值为10、7、5的二维岩石模型,K值越大,裂缝数量越多。图6(d)为网格剖分图,通过网格剖分为小单元格可以有效地计算电参数。

图6 二维岩石裂缝模型

实验使用COMSOL Multiphysics®仿真软件建立K值为7的二维裂缝模型,研究静电场对复杂页岩裂缝模型的影响,如图6(b)所示。再设置每一相的材料属性,其中复杂裂缝内含物为水介质(介电常数设为80),背景介质为岩石(介电常数设为4)。外部基体是边长为70 mm的正方形,内部不同宽度的线条代表不同孔径大小的裂缝,图6(b)中不同宽度的线条分别代表2 mm、0.8 mm、0.4 mm、0.2 mm不同孔径大小的裂缝。由于页岩裂缝呈现各向异性特征,故电位移矢量和电场强矢量之间与介电张量相关联。当在一个方向上加载电压时,只能得到一个介电常数的分量值。为了求得介电常数的4个分量值,则分别从X方向和Y方向加载两次静电场(10 V电压),如图7所示。图7(a)和图7(b)分别为X和Y方向加载电压示意图,图7(c)和图7(d)分别为X和Y方向电场图。

图7 裂缝网络加载电压以及电场图

为了验证正交方法在升尺度中的应用,本实验先将网络裂缝网格剖分为4个区域并依次正交化,并放入图1所示的升尺度结构中,得到图8的正交化升尺度过程。如图8所示,图8(a)为K值为7的裂缝模型,图8(b)为分割四个区域的裂缝网络,图8(c)为升尺度正交结构。本实验将升尺度正交结构的电参数和原裂缝网络的结果进行比较,验证正交方法在升尺度过程中的可行性。

图8 正交模型在升尺度中的应用

3.2 传统升尺度模型

当给定页岩裂缝模型的同时也确定了它的K值和介电参量。为了更加精细表征每一块裂缝的物性特征,按图2(d)所示方法,将图6中K值为7的原复杂裂缝模型通过网格剖分为四个等面积的小尺度裂缝网络。先分别求出每个网格的孔隙度,再通过与传统电特性理论模型相结合求出每一块的介电参量值,将其代入图2(e)对应的四个块状区域里面,则完成了从小孔隙裂缝网络到大块状网络的升尺度过程。文中电特性理论模型采用了LLCM和CRIM传统模型。将图2(d)中求出的四个区域的孔隙度分别带入到公式(5)和公式(7)中求出四个区域的介电参量,接着将其结果带入图2(e)的升尺度模型,求其整体的介电参量值,这样便可以得到LLCM和CRIM传统升尺度模型的介电参量值,再与原始裂缝的介电参量值进行对比。

4 结果和分析

图9分别为正交结构的εxx和εyy介电参量的上下界取值范围,并与原裂缝的介电参量值进行比较。从图中可以得到原裂缝的εxx和εyy两个介电参量值均落在正交结构的上下界之间,这表明了正交结构能够较高地还原原裂缝的电特性;上下界包含原裂缝网络的电特性值,证明了该正交结构的可行性。

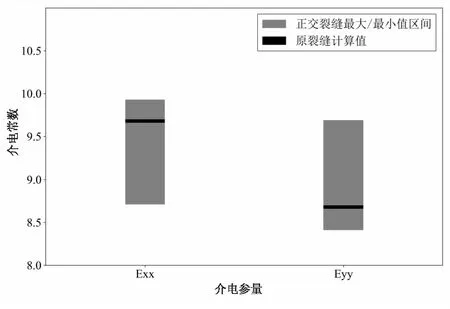
图9 正交结构单元不同介电参量值的取值范围

图10为原裂缝模型介电常数与正交升尺度模型和传统升尺度模型(LLCM和CRIM)的介电常数对比。从图10可以看出,正交升尺度模型的介电参量值与原裂缝模型的误差较小,相对误差值为1%。而传统电参数升尺度模型(LLCM和CRIM)与原裂缝模型误差较大,相对误差值分别为53%和61%。该结果表明,相对于传统电特性模型,复杂裂缝网络更加适用于升尺度过程。

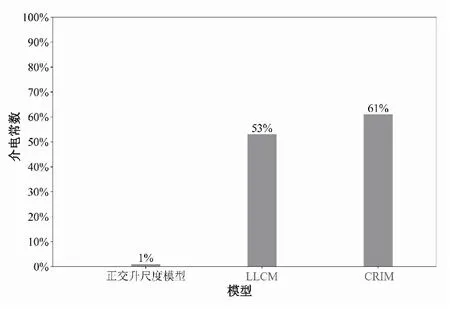
图10 不同模型与原裂缝模型的相对误差值

5 结束语

该文利用计算机仿真技术对特定K值下的复杂裂缝网络进行建模。实验使用了正交化方法,将原始裂缝网络在主方向的电特性映射到正交结构的主裂缝。为了保留原始裂缝的各向异性特征,在此正交结构的基础上加入了各向异性内含物椭球,可以获得正交结构等效电特性的上下界。结果表明正交结构的上下界能够包含原裂缝网络的电特性,为正交化方法的可行性提供了理论支撑。

同时为了验证该方法的可行性和适用性,分别将分割后的正交结构和传统电参数理论模型在升尺度方法中应用,并与原裂缝网络的电参数值进行比较,结果表明正交升尺度模型的电参数值与原裂缝网络值误差较小,而传统电参数模型的电参数误差值较大。本实验结果突出正交化方法在页岩储层升尺度和电特性模型构建中的潜力。