线导鱼雷动力电池管外激活发射初始弹道研究

丁 浩 ,孙乃葳 ,黄 波

(1.海军潜艇学院 导弹兵器系,山东 青岛,266199;2.中国船舶集团有限公司 第705 研究所,陕西 西安,710077)

0 引言

对于电动力鱼雷而言,采用管内激活发射方式时,动力电池注液激活后,一旦发生故障鱼雷未能及时出管,就会对发射艇产生严重的安全隐患[1]。而采用管外激活发射方式时,鱼雷出管后动力电池才激活启动,能够有效提高鱼雷的使用安全性,这种方式已被外军所采用[2]。管外激活发射方式下,鱼雷出管的初始阶段,其动力系统、控制系统等都未正常工作,弹道控制难度大,而鱼雷初始弹道对其后续弹道的稳定性有直接的影响。国内诸多学者都对鱼雷初始弹道展开了相关研究。刘凯等[3-4]研究了管制舵角和鱼雷衡重特性对鱼雷初始弹道的影响;李宗吉等[5]对发射参数不同时鱼雷初始弹道进行了建模和仿真分析,周杰等[6]对UUV 发射鱼雷初始弹道进行了研究;文钢[7]和张岳青[8]等分别对水雷、鱼雷的入水弹道进行了仿真分析。在管外激活弹道方面,主要开展了无线导方式下的弹道研究[1-2]。现代鱼雷为提高其目标搜索能力和水声对抗能力,大都装备了线导系统[9]。而管外激活发射方式下线导鱼雷初始弹道还未见有成熟的研究成果。因此,文中以管外激活发射线导电动力鱼雷为研究对象,建立线导鱼雷初始弹道模型并进行仿真,从而对不同发射条件对初始弹道的影响进行分析。

1 动力学模型

1.1 线导鱼雷管外激活初始弹道分析

线导鱼雷离艇后的初始弹道是指鱼雷发射离艇后,直至鱼雷弹道稳定(速度稳定、姿态可控)的初始非稳定段。该阶段的鱼雷弹道除了受到自身流体动力特性的影响外,还受到其尾部线导导线布放软管的拖拽。鱼雷离艇后的初始阶段由于航速波动较大,弹道控制难度较大(尤其是俯仰角),是水下弹道中最关键的阶段[10]。相比管内激活发射方式,管外激活发射方式主要在离艇后的初始弹道阶段存在较大差异,特别是鱼雷的纵向运动会受到较大影响,故重点研究鱼雷在垂直平面的初始弹道。

1.2 线导鱼雷管外激活出管过程动力学分析

鱼雷线导导线布放软管为金属软管,发射时被鱼雷快速拖拽出管并布放在水中。该金属软管属于柔性刚体,释放过程涵盖外力拖拽、自身伸张和流体动力等复杂因素,很难建立准确的动力学模型。对金属软管释放过程进行分析可知:整个释放过程很快,其自身的伸张性表现很弱;金属软管的刚度使其流体外形呈现径向小幅度的不规则变化,其径向的流体动力可以忽略;而金属软管的拖拽力对鱼雷初始弹道有直接影响,故对其进行重点分析[10]。

假设质量为 Δm的金属软管所受拉力为F,其在 Δt时间内速度由0 增至鱼雷速度v,由动量定理可得

式中,Δm=ρg·v·Δt,ρg为金属软管密度,由此可得

式中:M为金属软管的总质量;Lg为金属软管的总长度。

同时还有一部分拖曳力用来克服海水摩擦阻力,设为D,则有

式中:ρ为海水密度;Ωt为金属软管沾湿面积,Ωt=πdLt,d为金属软管的直径,Lt为拉出的金属软管长度;Cx为摩擦阻力系数,且

其中,Re为雷诺数。则鱼雷放线金属软管所受拖曳力为

当金属软管全部拉出后,便解脱同鱼雷的连接,此时金属软管所受拖曳力很小,可忽略。

1.3 线导鱼雷管外激活出管纵向运动模型

假设线导鱼雷放线金属软管对鱼雷的拉力为TL,其与金属软管所受拖曳力TR互为作用力与反作用力。将TL沿半速度坐标系分解为TLx和TLy,假设TLx与TL的夹角为η,鱼雷弹道倾角为 Θ,金属软管与水平面的夹角为 ϕ,如图1 所示。

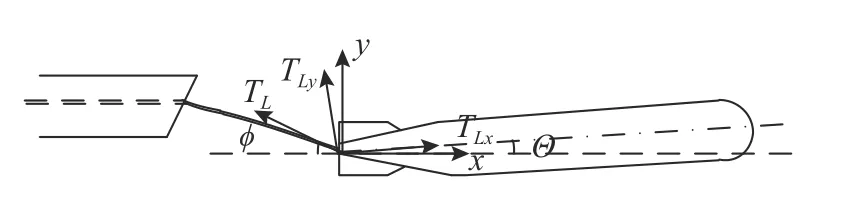
图1 线导鱼雷出管受力分析示意图Fig.1 Schematic diagram of forces analysis for wireguided torpedo out of tube

设鱼雷沿坐标轴的位移分别为x、y,由于金属软管随鱼雷出管,因此可认为其位移同鱼雷一致,则有

令η=Θ+ϕ,可得

线导鱼雷纵向运动简化方程组可写为

式中,Lw为鱼雷浮心与雷尾的距离,其他参量含义见文献[11]。

2 仿真与分析

2.1 仿真参数设定

以国外某型电动力鱼雷为研究对象,在鱼雷发射出管后,动力电池激活前,进行横舵管制,此段弹道为非控弹道。根据目前鱼雷电池技术的发展情况,假设鱼雷动力电池激活时间tA为10 s;金属软管的总长度Lg=50 m;鱼雷横舵管制舵角 δe不易过大或过小,否则极易导致鱼雷沉底或跳水[11],故取δe=0、1°、3°;鱼雷出管速度v0一般为8～22 m/s[1],故取v0=12、15、18 m/s;鱼雷流体动力参数取自参考文献[11];设鱼雷以水平姿态发射出管,横滚忽略不计,讨论以上各参数取不同值时,对鱼雷非控段垂直面初始弹道以及航行姿态的影响。

2.2 横舵管制舵角对垂直弹道的影响

设鱼雷出管速度v0=15 m/s,分别取鱼雷横舵管制舵角 δe=0、1°、3°,对线导鱼雷管外激活垂直面初始弹道进行仿真,结果如图2～图5 以及表1 所示。

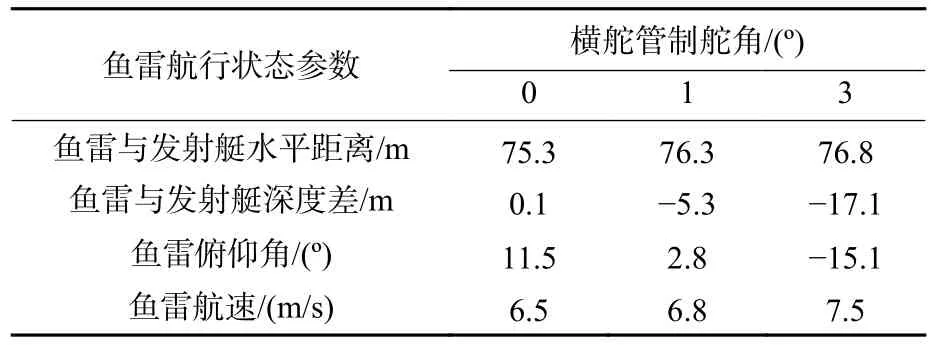
表1 δe 不同时的仿真结果(t=10 s)Table 1 Simulation results when δe changes (t=10 s)

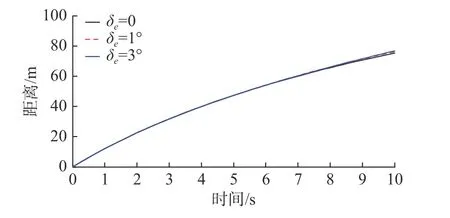
图2 δe 不同时鱼雷与发射艇的水平距离变化曲线Fig.2 Horizontal distances between torpedo and launch boat when δe changes

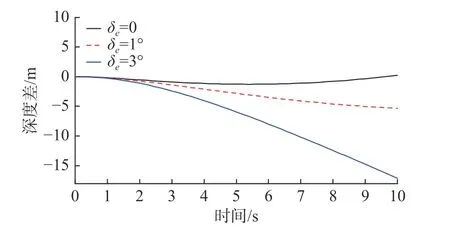
图3 δe不同时鱼雷与发射艇的深度差变化曲线Fig.3 Depth differences between torpedo and launch boat when δe changes

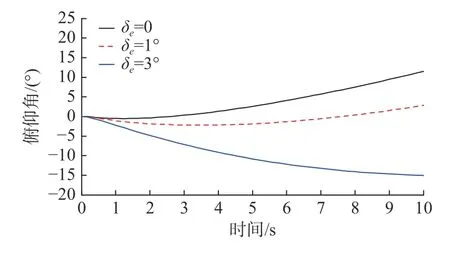
图4 δe不同时鱼雷俯仰角变化曲线Fig.4 Torpedo pitch angels when δe changes

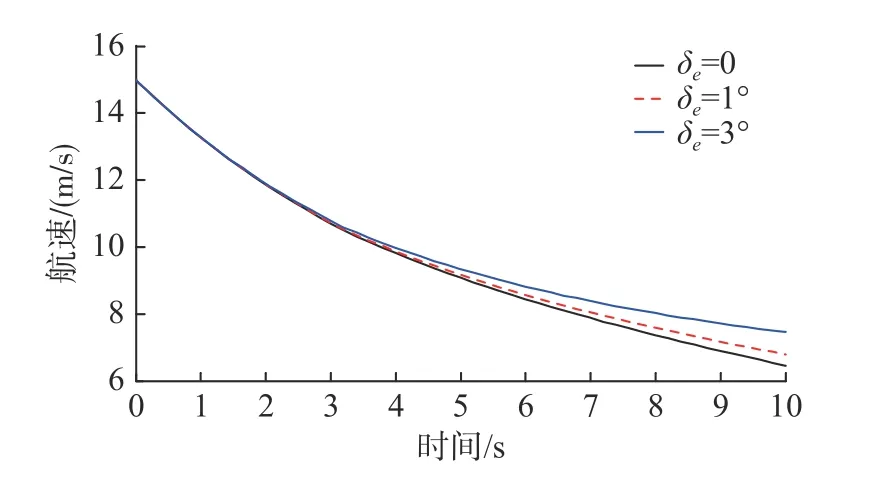
图5 δe不同时鱼雷航速变化曲线Fig.5 Topedo velocities when δe changes

由仿真结果分析可知,当鱼雷出管速度v0不变时,δe对鱼雷与发射艇的水平距离影响不大,水平距离变化曲线基本保持一致。鱼雷与发射艇的深度差随 δe的增大呈减小趋势,当 δe=0 时,深度差始终保持在0 附近;当 δe=3°时,深度差随时间下降最为明显,其中“-”号表示鱼雷位于发射艇下方。从鱼雷使用安全性的角度考虑,深度差不宜接近于0,以免出现雷艇相撞的事故;同时,深度差也不宜过小,以免出现鱼雷沉底现象。鱼雷俯仰角随 δe的增大同样呈减小趋势,当 δe=1°时,鱼雷俯仰角稳定在0 附近。从鱼雷航行姿态的控制角度考虑,鱼雷初始弹道俯仰角不宜过大或过小。鱼雷航速随时间的减小幅度随 δe增大而减小。当 δe=0 时,鱼雷航速的最大减小幅度为57.3%;当 δe=3°时,鱼雷航速的最大减小幅度为50.7%。

综合考虑鱼雷初始弹道安全性以及鱼雷姿态控制等因素,在此仿真条件下,取 δe=1°是比较理想的。

2.3 鱼雷出管速度对垂直弹道的影响

令 δe=1°,分别取v0=12、15 和18 m/s 进行仿真,其他仿真参数同前,仿真结果如图6～图9 及表2所示。

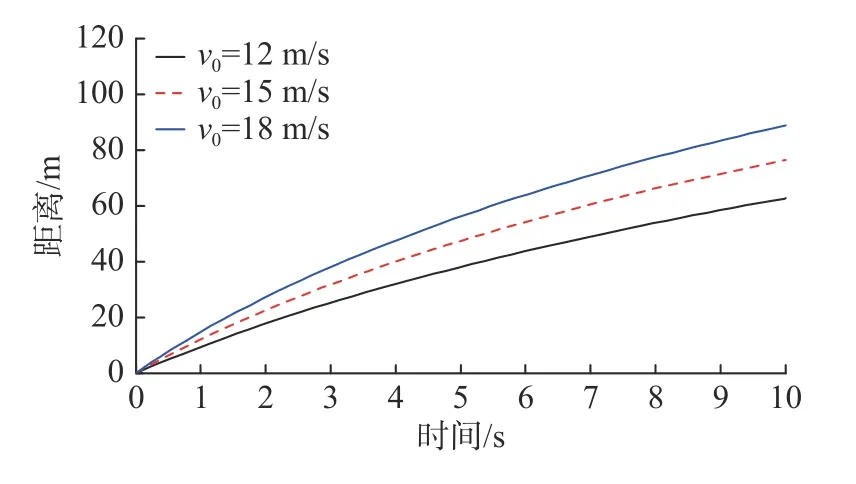
图6 v0取不同值时鱼雷与发射艇的水平距离变化曲线Fig.6 Horizontal distances between torpedo and launch boat when v0 changes

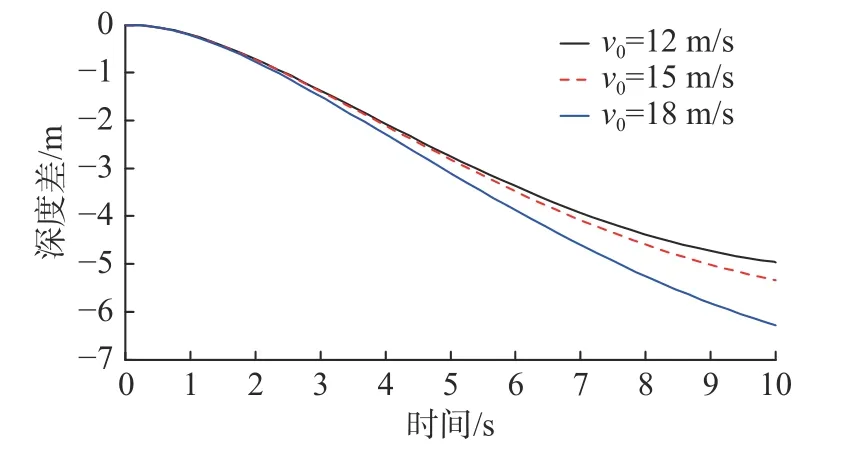
图7 v0不同时鱼雷与发射艇的深度差变化曲线Fig.7 Depth differences between torpedo and launch boat when v0 changes

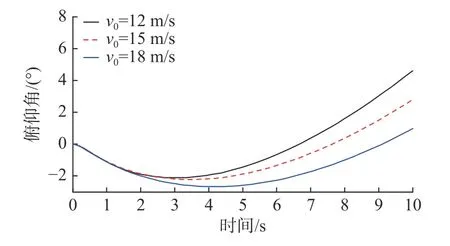
图8 v0不同时鱼雷俯仰角变化曲线Fig.8 Torpedo pitch angels when v0 changes

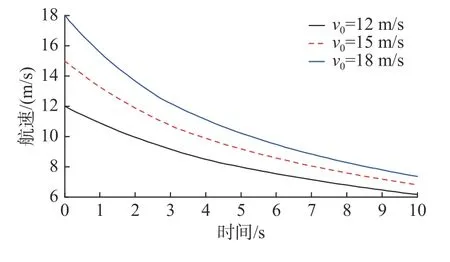
图9 v0不同时鱼雷航速变化曲线Fig.9 Topedo velocities when v0 changes

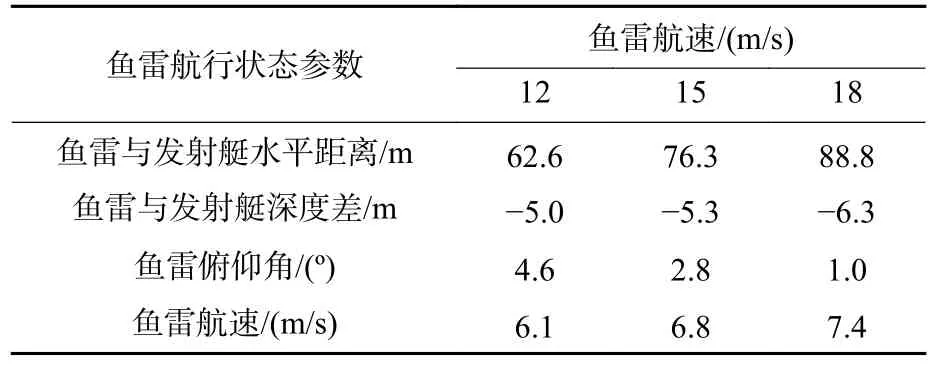
表2 v0不同时的仿真结果(t=10 s)Table 2 Simulation results when v0 changes (t=10 s)

由仿真结果分析可知,当 δe不变时,鱼雷与发射艇的水平距离随v0的增大而增大,且增大幅度较大。鱼雷与发射艇的深度差随v0的增大而减小,且减小幅度较小。鱼雷俯仰角随时间呈先减小后增大的趋势,拐点出现在金属软管全部拉出解脱同鱼雷的连接后,且俯仰角随v0的增大而减小。鱼雷航速随时间的减小幅度随v0的增大而增大,当v0=12 m/s 时,鱼雷航速的最大减小幅度为49.2%;当v0=18 m/s 时,鱼雷航速的最大减小幅度为59.4%。

可见,从鱼雷初始弹道安全性以及鱼雷出管的姿态控制考虑,增大鱼雷的出管速度是有利的。

3 结束语

在对线导鱼雷管外激活出管过程动力学进行分析的基础上,建立线导鱼雷出管纵向初始运动模型,并进行计算机仿真,分别针对不同横舵管制舵角和不同出管速度对鱼雷初始弹道以及航行姿态的影响进行了定量分析,结果表明:通过选取适当的 δe(δe=1°)以及增大v0,可使线导鱼雷获得安全的管外激活初始弹道以及良好的姿态控制,线导鱼雷管外激活发射方式是可行的。文中结论是在对鱼雷动力学方程进行简化的基础上研究得到的,在实际中还存在若干干扰因素,如由发射艇体引起的鱼雷流体动力干扰等,对此还需开展进一步研究工作。