航行器水面滑行喷水推进特性研究

刘富强 ,周霖仪 ,孙 元 ,闫 靠

(1.中国船舶集团有限公司 第705 研究所,陕西 西安,710077;2.中国船舶集团有限公司,上海,200011)

0 引言

以鱼雷为代表的水下航行器因其具有水下打击威力大、隐蔽性好等特点,已成为海军水下攻防的主战装备[1-3]。然而,随着科技的飞速发展,舰船的综合性能尤其是航速得到大幅提高,为了有效追踪和攻击目标,鱼雷的最大航速至少应达到目标航速的1.5 倍,这对水下航行器的航速指标提出了更高的要求,进而给动力推进系统带来了更加严峻的考验。

喷水推进系统应用于水下航行器时,可以避开螺旋桨推进系统在轴系布置、传动方式等方面遇到的一系列技术难题,具有结构简单的优点,尤其在高航速、浅水抗气蚀性能上具有明显优势[4-5]。因此,对喷水推进技术的研究已成为目前世界各国的研究热点。

喷水推进系统的研究最早可以追溯到300 多年前。1661 年,Toogood 与Hayes 获得了英国的专利,此后有关喷水推进装置的研究从未停止[6]。19世纪末,喷水推进被应用于船舶推进领域。1865年,英国建造了2 艘喷水推进的炮舰,其排水体积为1 180 m3[7]。1962 年,苏联首次在水翼艇上采用喷水推进装置,美国波音公司也在“小水枪”号试验艇上采用离心泵作为喷水推进泵[8]。1974 年,英国首先在其核潜艇“Sovereign”上使用喷水推进系统,美、法等国也先后在核潜艇上采用了喷水推进方式。美国海军最新型“海狼”级攻击核潜艇即采用喷水推进方式[9]。

喷水推进装置在水下航行器上的应用主要体现在高性能鱼雷上,如俄罗斯的某型喷水推进鱼雷航速高达70 kn[10]。近年来,国内外学者对于水面航行器喷水推进也做了大量的研究。荷兰科学家深入探索了喷水推进装置与船体之间的相互作用,制定了一套喷水推进船模自航试验预报推进性能的试验方法和规程,奠定了喷水推进的试验基础[11-12]。

随着计算机水平的不断进步,计算流体力学(computational fluid dynamics,CFD)的发展为喷水推进器的设计和研究提供了平台。Park 等[13-14]应用雷诺平均纳维-斯托克斯(Reynolds-averaged Navier-Stokes,RANS)方程对船舶用喷水推进装置进行了数值仿真,模拟了内流场中复杂的粘性流和翼梢涡流,通过仿真对喷水推进装置的推力和转矩性能做出预测,仿真结果与试验结果一致。苑龙飞等[15]采用CFD 方法对喷水推进系统在浅水高速工况下的适应性问题进行了仿真,得出单级喷水推进系统适应性较差,气蚀严重,双级对转水泵推进系统可提高高速水下航行器的浅水抗空泡性能的结论。刘成勇[16]提出了适用于浅水高速的喷水推进系统设计方法,采用数值方法开展喷水推进系统研究。

综合国内外已有研究发现,对大尺度航行器喷水推进研究较多,其内流道浸没深度大;而针对小尺度航行器近水面喷水推进系统流道内流场特性和流体动力特性研究较少。小尺度航行器近水面喷水推进内流道浸没较浅,涉及多相流动、湍流以及内流道配置等一系列问题,试验研究较为复杂,亦不经济。因此,文中提出一种数值仿真的方法研究航行器近水面喷水推进的流场特性和流体动力特性。该方法基于STAR-CCM+数值仿真软件,选用SST(shear stress transport)k-ω湍流模型,采用多重参考系(multiple reference frame,MRF)模型和理想水泵模型构建航行器水面滑行喷水推进数值仿真模型,对航行器在近水面不同模拟水泵压力和浸没深度下的水面滑行工况进行仿真,研究其水面滑行过程中的流场特性和流体动力特性。

1 数值仿真模型建立

1.1 数值方法

航行器水面滑行问题属于气液两相问题,在湍流的非直接数值仿真中,应用最广泛的是时均性质的RANS 方程,控制方程包括连续性方程、动量方程和相体积方程[17-18],分别为

式中:αq为流体微元中第q相体积分数;v为流体微元的速度矢量;ρq为第q相密度;和分别为第q相和第p相之间的质量传递速率;n为总相数;ρm、µm分别为流体微元各相平均密度和动力黏度。

湍流模型采用SSTk-ω模型[19],其基于Baselinek-ω湍流模型,考虑了湍流剪切力的输运问题。采用MRF 模型[18,20]将航行器运动规律以平移速度的方式赋予参考系,把相对速度代入控制方程进行计算。采用理想水泵模型模拟文中研究轴流水泵喷水推进。针对水面航行问题,采用流体体积(volume of fluid,VOF)方法模拟气液两相界面问题,可以更深入地观察自由液面的变化,以获得更好的流场特性和流体动力特性[21]。

1.2 SST k-ω 湍流模型

湍流是自然界中最为常见的一种流动现象,在工程技术领域,大多数流动都是湍流流动,其属于极为复杂的非稳态、有旋不规则运动,具有随机脉动性和各向不均匀性,对于流场的压力、速度等分布具有明显的影响。湍流仿真的方法主要有直接数值仿真(direct numerical simulation,DNS)、RANS和大涡仿真(large eddy simulation,LES)等,文中采用工程常用的RANS 湍流模型求解航行器水面航行的流场。

在对航行器水面航行数值仿真中,可以采用的RANS 湍流模型包括k-ε湍流模型和k-ω湍流模型,两者在工程实践中都得到了广泛应用。常用的k-ω湍流模型有3 种,即Standardk-ω湍流模型、BSL(Baseline)k-ω湍流模型和SSTk-ω湍流模型。根据湍流模型的使用要求和相关文献的研究结论,文中在模拟航行器水面航行时选用SSTk-ω湍流模型。SST 湍流模型基于BSLk-ω湍流模型,考虑了湍流剪切力的输运问题,在流场计算中具有较好的精度和可行度。

Menter[19]认为BSL 模型的缺陷主要是由于对涡粘性的预测不当引起的,可通过给涡粘性设置限制器的方法来解决,并由此提出SSTk-ω湍流模型。基于BSL 湍流模型,SST 湍流模型作如下改进

式中量的解释参见文献[19]。

1.3 MRF 运动参考系

MRF 模型是Issa 等[20]于1994 年提出的一种针对多区域计算较为简单的定常计算模型。定义坐标系ox′y′z′固连于绕流物体,并且相对于惯性坐标系oxeyeze,坐标系ox′y′z′的原点位置矢量为r0,平移速度为vt,角速度为 ω。对于计算域内的任一流体微元,假设其相对于坐标系ox′y′z′原点位置为r,

则该点在惯性坐标系oxeyeze中的绝对速度为

式中,vr为流体微元在运动参考系ox′y′z′的相对速度。

采用运动参考系方法,将绕流物体的运动规律以平移速度或旋转速度的方式赋予参考系,然后把相对速度代入控制方程进行计算。相对速度形式的动量守恒方程需要添加额外的体积力,主要用于描述旋转和加速等非惯性运动,包括科氏加速度、向心加速度等。运动参考系中流体质点受到的体积力有

式中:α和a分别为运动参考系相对于惯性参考系的旋转加速度和平移加速度;等号右边各求和项依次为科氏加速度、向心加速度、角加速度、平移加速度和重力加速度。

1.4 VOF 波

STAR-CCM+软件提供VOF 波建模,VOF 波模型用于模拟轻流体和重流体间交界面上的表面重力波。STAR-CCM+提供VOF 波模型包括平波、1 阶波、5 阶波、椭圆余弦波、叠加波和不规则波等。文中所研究的航行器静水面航行问题,采用平波模型构建气液交界面,通过设置平波水面上的点和水面方向模拟航行器水面航行工况。图1为文中研究航行器水面喷水推进初始流场液面示意图,蓝色区域表示空气域,红色区域表示水域。

图1 航行器静水面液面示意图Fig.1 Schematic diagram of static water level of a vehicle

1.5 理想水泵模型

采用轴流水泵喷水推进的双模航行器在水面滑行时不仅其主体表面受到流体阻力,喷水推进内流道也受到较大的阻力,尤其是轴流泵高速运转时。因此,文中对航行器轴流水泵喷水推进特性进行分析,探究航行器水面滑行内流道的流场特性和流体动力特性。研究中为了便于计算,不针对轴流泵的具体设计作细致研究,采用CFD 理想水泵模型模拟轴流泵增压过程[19]。

在数值计算过程中,喷水推进系统产生的推力由CFD 模拟理想水泵模型的压差 ΔP提供,当航行器水面航行处于匀速直线运动时,喷水推进系统产生的推力Tt的水平分量与航行阻力Fd平衡,即

式中:α1为航行器水面滑行的攻角;A1为轴流泵安装处环形流道面积。

2 可行性验证

Timothy 等[22]利用水池进行拖曳试验,对不同直径回转体的滑水问题进行了一系列的试验研究。基于航行器水面航行的数值仿真模型和文献[22]中直径88.9 mm、长度1 422 mm 的回转体,对回转体以12.19 m/s 速度、6°攻角进行一定浸没深度滑水工况数值仿真。

图2 展示了回转体在沾湿长度为4 倍直径滑水状态下的试验照片和数值仿真计算结果。仿真结果可知,在滑水过程中,运动体尾部飞溅产生大量的水花,与试验照片吻合性较好。在数值计算过程中,对回转体滑水的升阻力进行监测,该工况下数值计算升力为19.37 N,阻力为10.21 N。

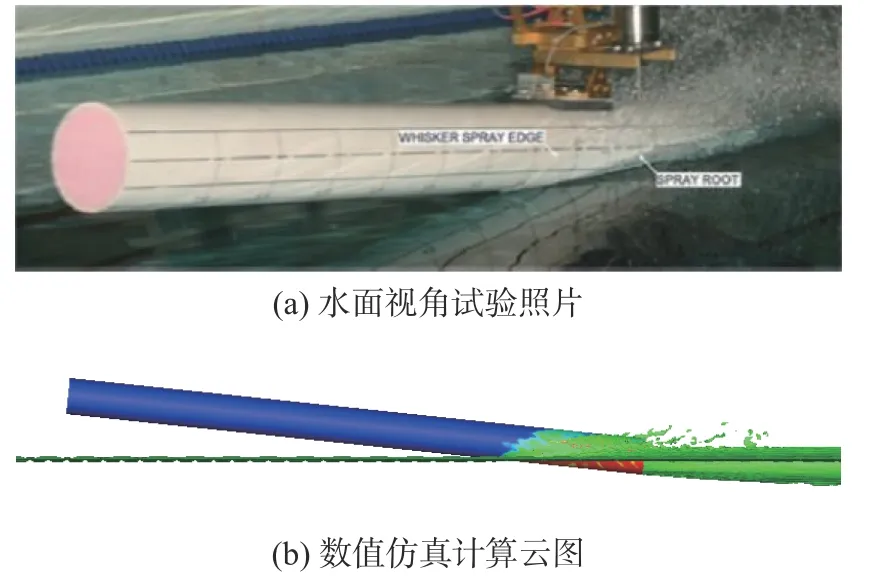
图2 滑水试验照片与数值仿真对比Fig.2 Comparison of experiment photo and numerical simulation

对升阻力特性进行无量纲化表示,升力系数为0.032 9,阻力系数为0.017 3。对比文献中得到的升力系数0.033 8,阻力系数0.017,升力系数误差为-2.5%,阻力系数误差为2.28%,均小于5%,满足工程误差。

式中:Fl和Fd分别表示航行器航行过程中受到的升力和阻力;ρ表示运动环境介质的密度,文中取水的密度998 kg/m3;v和D分别为航行器的运动速度和直径。

基于前文提出的航行器水面航行数值计算方法,对经典文献中回转体水面滑行进行相同工况的数值仿真,数值仿真流场吻合性较好,流体动力计算结果与试验值相比误差不超过5%,在工程误差范围内。因此,文中提出的航行器水面航行数值计算方法可行,可用于后文对航行器轴流水泵喷水推进流场特性和流体动力特性研究。

3 数值仿真计算

文中所研究航行器水面滑行阶段动力推进方式采用电动力喷水推进。电动力航行器的优势在于航行器所需能源仅需携带蓄电池,结构简单。航行器采用喷水推进可以避免螺旋桨推进易产生空化从而导致推进效率低的问题。

水下喷水推进航行器一般采用周向进水模式，其能够避免流道内非均匀流的出现,模型示意图如图3 所示。文中提出一种新型的双模航行器,其由航行器主体和前水翼2 部分组成,可以实现水面自由滑行和水下航行,双模航行器水面滑行效果图如图4 所示。

图3 周向进水水下航行器模型示意图Fig.3 Schematic diagram of circumferential inlet undersea vehicle model

图4 双模航行器水面滑行效果图Fig.4 Rendering of a dual-mode vehicle planing

文中所研究的双模航行器在水面滑行阶段若采用周向进水,轴流泵在吸水的同时会夹杂大部分空气进入到内流道,夹杂空气的存在将严重影响轴流泵的工作效率,因此文中研究的双模航行器喷水推进内流道配置采用单侧进水设计,航行器在水面滑行过程中,通过下端进水可有效避免流道内夹杂空气现象的发生。航行器尾部结构及电动力喷水推进内流道模型如图5 所示。

图5 航行器尾部结构以及电动力喷水推进模型Fig.5 Tail structure of a vehicle and electro-dynamic water-jet propulsion model

航行器喷水推进系统工作过程中电机高速转动,通过联轴器带动转轴将动力传递至轴流泵动叶。轴流泵在高速转动过程中,进水口吸水通过轴流泵增压后将水向后高速喷出,从而使航行器获得推力。

在计算机软件仿真过程中,一般借助网格进行求解。文中采用切割体网格和棱柱层网格对流域网格进行划分,采用表面重构对网格与结构体衔接处进行优化。同时针对航行器内流道及水面区域采用体积控制法进行局部体加密。

在网格模型和计算域保持不变的条件下,采用体形状内不同网格加密尺度对航行器内流道进行局部加密,得到网格单元总数目分别为360 万、450 万、570 万和684 万4 种计算域网格结果。通过对水面恰好淹没航行器尾端特定工况进行数值仿真结果对比,验证网格数量无关性,此时航行器速度、攻角和 ΔP分别为7.5 m/s、10°和60 kPa。

表1 为不同网格数量下航行器特定工况水面滑行阻力特性,360 万网格数量模型阻力明显高于其他网格数量计算值;450 万、570 万和684 万网格数量模型阻力计算值几乎相同。考虑网格数量较大时,增加计算机运行负荷,计算耗时增长。因此选用570 万网格数量模型用于后续航行器水面喷水特性数值仿真计算。图6 为570 万网格数量模型航行器网格示意图,航行器内流道网格平均尺寸为4 mm,网格质量较好。

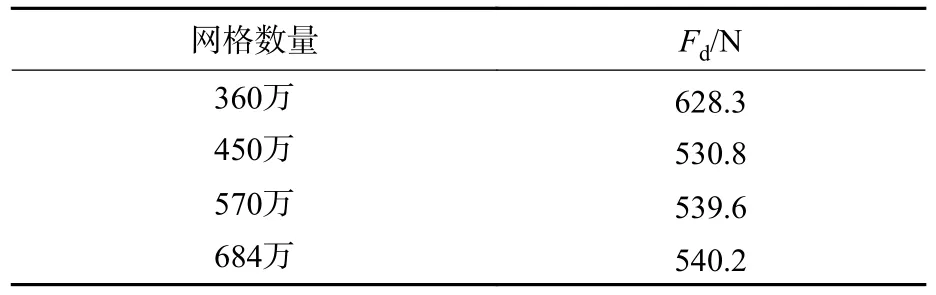
表1 不同网格数量特定工况水面滑行阻力特性Table 1 Drag characteristics of planing at a specific condition under different mesh quantity

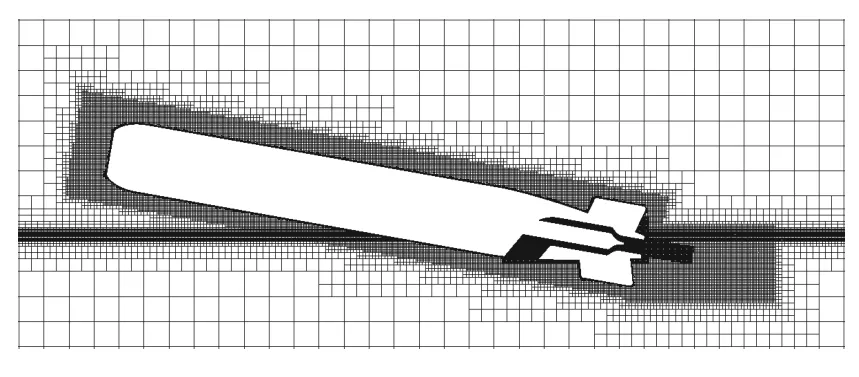
图6 航行器网格局部Fig.6 Local mesh of a vehicle

3.1 不同ΔP 下航行器水面滑行仿真分析

在对双模航行器主体喷水推进系统内外流场仿真时,根据包含内流道的航行器主体总阻力,不断调整模拟水泵模型的压力值,最终使得航行器主体的阻力与喷水推进系统产生的推力平衡,使航行器主体在水平方向处于受力平衡状态。对航行器主体在不同 ΔP作用下的水面滑行过程进行数值仿真,研究内流道的流场特性以及航行器主体的流体动力特性,航行器主体水面滑行速度为7.5 m/s,攻角为10°,液面高度恰好淹没航行器尾部,文中所研究航行器内流道轴流水泵安装处环形流道面积A1=0.009 076 m2。

表2 为航行器主体在水面滑行时不同ΔP作用下模拟推力值和总阻力值。观察发现,随着ΔP的增大,航行器主体阻力值明显增大。当ΔP=60 kPa 时,水泵推力的水平分量Ttx=536.3 N,该工况下航行器主体的总阻力Fd=539.6 N,两者差值为总阻力的0.61%,小于1%。此时可认为轴流水泵推力与航行器主体的总阻力平衡。

表2 不同ΔP 下航行器水面滑行理想水泵推力与总阻力Table 2 Ideal pump thrust and total drag for vehicle planing under different ΔP

在不同ΔP下水面滑行工况的数值仿真中,对航行器的外流场及内流道流场进行了对比。图7为航行器主体不同 ΔP时水面滑行的密度云图,其中红色为水介质,蓝色为空气介质。观察发现,当ΔP=0,即水泵不工作时,几乎没有水进入内流道。表3 为航行器稳态航行时,对其喷水特性及流体动力特性的监测值,其中:M为内流道喷水出口的流量;vout为出口的平均喷水速度;Fl为航行器主体的总升力;Fd_out和Fl_out为航行器外壳体的阻力和升力;Fd_in和Fl_in为航行器内流道的阻力和升力。

表3 不同 ΔP下航行器喷水特性及流体动力特性Table 3 Water-jet characteristics and hydrodynamic characteristics of a vehicle under different ΔP

当 ΔP=0 时,航行器内流道出口流量仅为0.347 kg/s,明显小于其他压力工况出口流量,出口平均速度为1.59 m/s;观察其阻力分布情况发现,内流道阻力为-0.57 N,近似为零,航行器主体的阻力全部体现为外壳体阻力,流道内几乎没有液体流动。此时航行器内流道升力为负,属于压差升力,这主要是由于初始状态下内流道内部充满水,而在稳态航行时流道内的水未完全排出导致,该结果与图7(a)水面滑行密度云图所呈现的几乎没有水进入内流道的现象相吻合。

对比图7 发现,当 ΔP存在时,水从进水口被吸入内流道,并完全充满内流道,无空气夹杂,进水效果良好,在流道出口向后高速喷出形成推力。图8和图9 分别为不同ΔP下航行器主体水面滑行的压力云图和速度云图。从图8 可知,在水泵前后有明显的压力变化,流场最高压力点位于泵后的高压区;从图9 可以发现,内流道出口有明显的高速射流出现。

图8 不同ΔP 下航行器水面滑行压力云图Fig.8 Pressure contours of vehicle planing under different ΔP

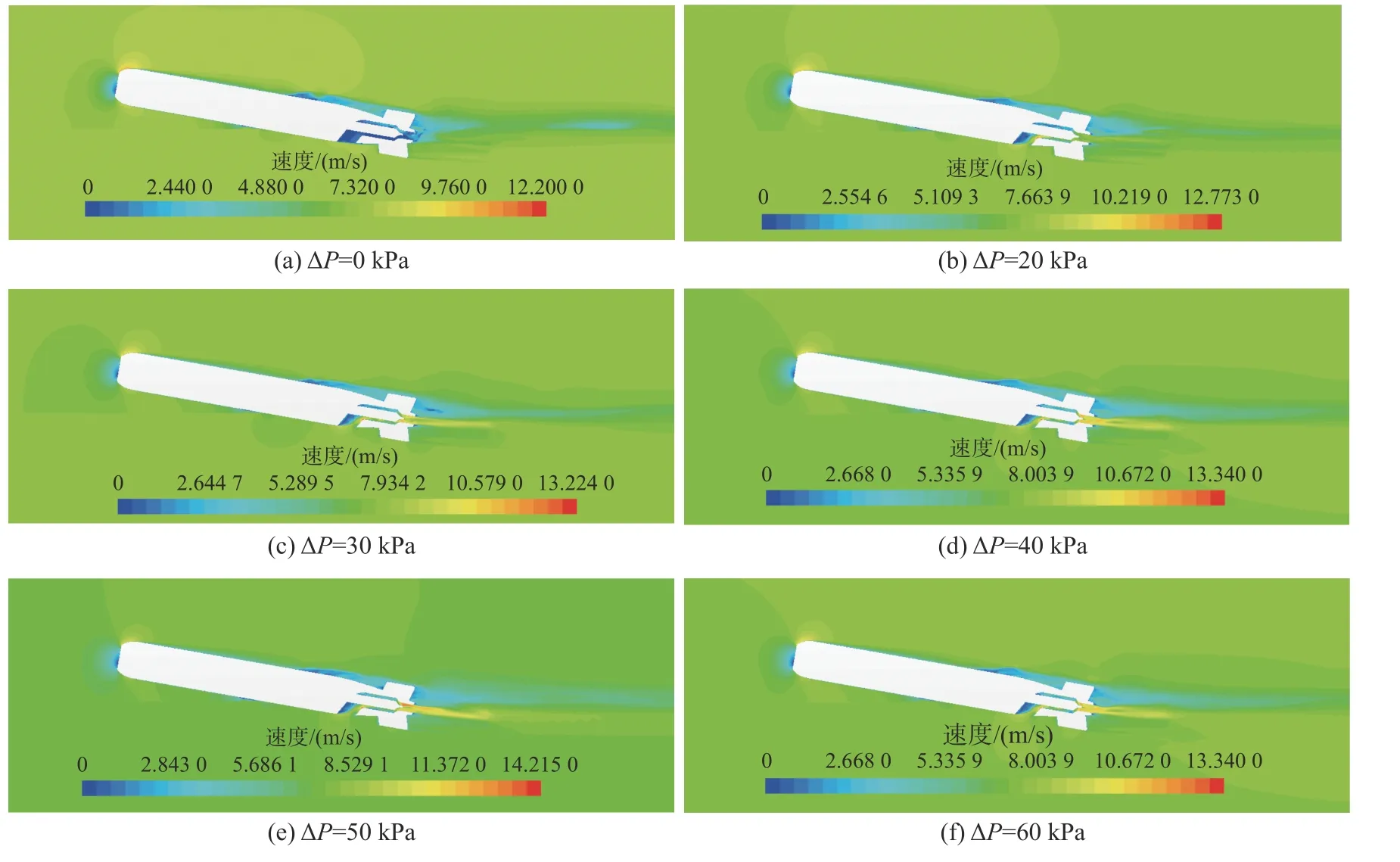
图9 不同ΔP 下航行器水面滑行速度云图Fig.9 Vehicle contours of vehicle planing under different ΔP

表3 中,随着 ΔP的增大,航行器内流道出口的质量流量和平均喷水速度逐渐提高。对航行器主体在不同工况下的流体动力特性进行监测,包括航行器外壳体和内流道的升阻力特性。观察发现,不同ΔP下航行器主体水面滑行过程中外壳体的阻力值约为140～150 N,升力值约为410 N,升阻力特性均无明显变化,不会对航行器壳体外流场产生较大影响。随着压力值的增大,内流道阻力明显上升,这一方面与流道内部水流速度增加,流道内摩擦阻力明显增大有关;另一方面则是由于流道收缩段前为高压区,对内流道有较大的压差作用力,主要体现为水平方向的阻力。

观察内流道升力特性发现,内流道升力为负,且随着压力值的增大,内流道升力的绝对值略微增大。内流道升力为负值的主要原因是,航行器主体水面带攻角滑行时,内流道收缩段后端高压区对内流道的压力作用斜向下,竖直方向表现为向下的升力。内流道升力绝对值略微增大,不同于阻力值变化明显的主要原因在于,航行器小攻角水面滑行内流道高压区作用力斜向下,主要体现为水平阻力,对于竖直方向的升力项贡献较小。因此,在航行器主体水面滑行流体动力特性分布中,阻力值随着内流道水泵压力变化明显,升力值变化不明显。

3.2 不同浸没深度下航行器水面滑行仿真分析

文中设计的双模航行器推进方式为喷水推进,要求航行器在水面滑行的过程中液面必须高于进水口才能满足进水需求,否则将可能影响轴流泵的工作效率。由于航行器在水面滑行过程中会受到波浪等扰动的影响,进水口附近液面高度也会发生变化,因此需对航行器主体在不同浸没深度水面滑行工况进行数值仿真,探究浸没深度对航行器内流道进水的影响。

通过3.1 节数值仿真发现,当 ΔP=60 kPa 时,水泵提供推力的水平分量为536.3 N,此时航行器主体总阻力为539.6 N,推力水平分量与阻力相平衡。但在研究中未考虑前水翼的阻力,在双模航行器水面滑行过程中该部分阻力仍需动力推进系统提供。文中双模航行器配置前水翼在70 mm 水下运动工况下计算得到的前水翼阻力为155 N,因此当 ΔP=60 kPa 时,轴流水泵推力将不再满足总阻力需求,需要提高水泵性能。表4 为 ΔP=60～100 kPa时航行器主体的推力水平分量和阻力特性,其中Fd_b为航行器主体阻力,Fd_t为航行器总体阻力。当 ΔP=90 kPa 时,Fd_t=805.5 N,此时Ttx=804.4 N,两者差值为总阻力值的0.14%。可认为当 ΔP=90 kPa时,航行器动力推进系统性能与航行器总体性能相匹配。

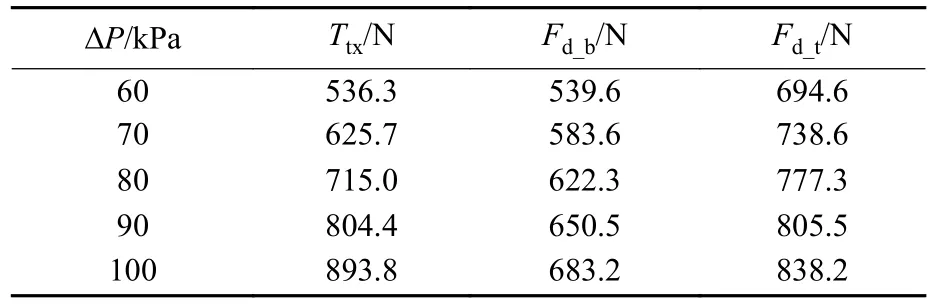
表4 不同ΔP 下航行器水平推力和阻力特性Table 4 Horizontal thrust and drag characteristics of the vehicle under different ΔP

采用单一变量法研究浸没深度h(为液面距离航行器内流道进水口的高度)对航行器主体以及内流道流场特性和流体动力特性的影响。设水面滑行速度7.5 m/s,攻角10°,ΔP=90 kPa,分别取h=2、20、40、60、80、100、120 mm。图10 为航行器主体在h=2 mm 时水面滑行的初始状态密度云图,此时水面恰好淹没进水口,初始状态下流道内充满水。

图10 h=2 mm 时航行器主体初始状态密度云图Fig.10 Density contour of main body of the vehicle at initial state with h=2 mm

比较稳定航行流场发现,当h=2 mm 时,航行器内流道进水效果较差。图11为h=2 mm 时,航行器主体水面滑行稳态密度云图和速度云图。从图11(a)可以发现,流道内夹杂大量空气,极大影响水泵效率;从图11(b)可以发现,流道内最高速度达到114.26 m/s,并且在高速区域主要表现为流道内空气的高速扰动。

图11 h=2 mm 时航行器稳态密度和速度云图Fig.11 Steady-state density and velocity contours of vehicle inlet at h=2 mm

图12 表征了航行器主体在不同浸没深度下流场的密度云图。观察发现,当h=20～120 mm 时,在轴流水泵作用下,水能够完全充满内流道,无空气夹杂,进水效果良好。图13 为航行器主体在不同浸没深度水面滑行的速度云图,当h＞20 mm 时,不同浸没深度工况航行器流道出口均有高速流体喷出,流域最大速度几乎相同,均为16.0～16.7 m/s。

图12 不同浸没深度航行器水面滑行密度云图Fig.12 Density contours of vehicle planing at different immersion depths

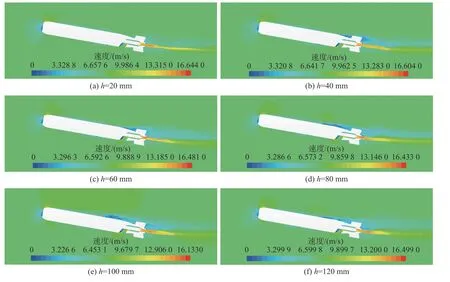
图13 不同浸没深度航行器水面滑行速度云图Fig.13 Velocity contours of vehicle planing at different immersion depths

对航行器主体不同浸没深度水面滑行过程中的流体动力特性进行监测,结果见表5。当h=2 mm时,流道出口流量33.3 kg/s,出口平均速度58.2 m/s,出口流量明显小于其他浸没深度下水面滑行出口流量,而出口平均速度是其他浸没深度航行器主体水面滑行出口平均速度的4 倍以上。这主要是由于h=2 mm 时,内流道出口高速出流时夹杂大量空气所致,与图11 所示的流场特性相吻合。

表5 航行器不同浸没深度水面滑行流体动力特性Table 5 Hydrodynamic characteristics of vehicle planing at different immersion depths

对比h＞20 mm 时航行器水面滑行阻力特性发现,随着航行器浸没深度的提高,航行器主体沾水面积增大,航行器壳体的阻力显著提高,而内流道阻力几乎不变,稳定在510 N 左右。观察其不同浸没深度升力特性,航行器内流道升力为负值,这主要与航行器带攻角航行喷水方向斜向下有关,且内流道升力稳定在-100 N 左右,主要体现为压差升力;航行器外壳体阻力随着浸没深度的增加逐渐提高,主要表现为沾水面积的增大,航行器外壳体摩擦阻力增大。

当h＞20 mm 时,航行器内流道流场特性和流体动力特性几乎不变,不再受浸没深度影响。

4 结论

文中基于STAR-CCM+数值仿真软件,采用MRF 运动参考系和模拟理想水泵模型构建航行器水面航行喷水推进数值仿真模型。对航行器在不同模拟水泵压力和不同浸没深度水面航行工况进行数值仿真,探究内流道的流场特性和流体动力特性,主要得到以下结论。

1)理想水泵模型能够很好地模拟轴流水泵吸水作用,水从进水口被吸入内流道,并完全充满内流道,无空气夹杂,进水效果良好,在流道出口向后高速喷出形成推力。

2)对比不同模拟水泵压力航行器内流道的流体动力特性发现,随着压力值的增大,内流道阻力明显上升。这一方面与流道内部水流速度增加导致摩擦阻力增大有关;另一方面与流道收缩段前高压区对内流道有较大的压差作用有关。内流道升力体现为负升力,随着压力值的增大,内流道升力几乎不发生变化。

3)对航行器主体在不同浸没深度水面滑行的数值仿真中发现,当航行器进水口浸没深度大于20 mm 时,航行器内流道进水效果不再受浸没深度的影响,进水效果良好。

文中采用简化内流道定常研究来探索航行器水面航行喷水推进特性,后续将针对航行器水面动态航行过程进行更深层次的研究,具体研究方向包括航行器的跨介质水面航行、多自由度运动特性等。