基于压力传感器阵列的AUV 姿态反演估计

王重阳 ,于化鹏 *,李子圆 ,2,赵德鑫

(1.军事科学院 国防科技创新研究院,北京,100071;2.哈尔滨工程大学 水下机器人技术重点实验室,黑龙江 哈尔滨,150001)

0 引言

自主水下航行器(autonomous undersea vehicle,AUV)可以在很少甚至没有人工干预下完成水下任务,自主导航是其完成各种任务的核心[1]。其加载的惯性导航系统(inertial navigation system,INS)根据加速度计和陀螺仪获得加速度和角速度数据,进而解算得到AUV 位置、速度和姿态等信息,不受外界干扰,具有高度自主性[2]。INS 误差随时间累积,导航精度会快速下降。为抑制误差累积,常采用多普勒计程仪(Doppler velocity log,DVL)作为辅助传感器,与INS 形成组合导航系统,以此提升导航精度[3]。然而,INS/DVL组合导航存在价格昂贵、占用空间大且功耗高等问题,不适用于小型化、低成本AUV,因此小型化、低成本自主导航技术成为研究热点。

仿生学研究表明,鱼类利用侧线系统可以感知体表压力,通过探测压力变化可以获取导航信息[4-6]。受此启发,研究人员提出许多利用压力传感器获取AUV 姿态和速度信息的方法:Vitale 等[7]在水下遥控航行器(remotely operated vehicle,ROV)上安装了多个压力传感器,利用伯努利原理进行公式推导,得到利用压强数据获取ROV 姿态和速度信息的方法,并指出压力传感器安装距离大于4 m时,能得到较好的姿态信息;Meurer 等[8-9]提出在AUV 姿态变化时采用压强数据估计速度的方法,并开展外场试验验证了所提速度估计方法的有效性。Baruch 等[10]利用最小二乘法得到利用压强数据估计姿态的方法及其克拉美罗界(Cramer-Rao lower bound,CRLB),并通过仿真试验分析压力传感器安装布局和AUV 尺寸对姿态估计的影响,从而得到压力传感器最优布局方案。上述研究主要采用仿真方法进行试验验证,同时开展了外场试验,但仅提出了速度估计方法。文中通过构建多层感知机(muti-layer perception,MLP)机器学习模型,提出一种基于压力传感器阵列的AUV 姿态反演估计模型,并通过外场试验验证了模型的有效性。

1 基于压力传感器阵列的姿态反演估计模型

AUV 表面压强是静态流体压强与动态流体压强之和。静态流体压强由设备所在深度决定,其计算公式为[10]

式中:ps为静态流体压强;p0为水面大气压;ρ、g和h分别为水的密度、重力加速度和设备深度。伯努利原理指出,在理想流体中动态流体压强与流体速度呈二次关系,即[8]

式中:pd为动态压强;v为流体速度;C为常数。

以装有4 个压力传感器阵列的AUV 为例,如图1 所示。

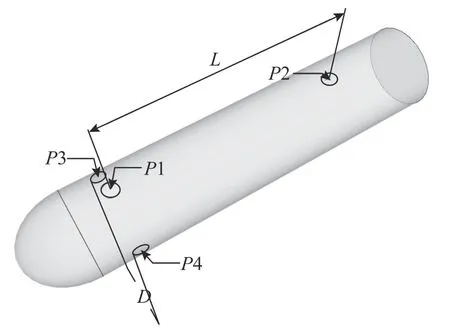
图1 AUV 示意图Fig.1 Diagram of AUV

此时,将AUV 近似为圆柱体,压力传感器编号分别为P1、P2、P3 和P4。P1 和P2 之间距离为L,P3 和P4 之间距离为D。p1、p2、p3和p4分别是P1、P2、P3 和P4 测量的压强数据。

考虑AUV 发生如图2 所示的姿态变化,即横滚角为0°,俯仰角从0°变为θ,根据三角函数公式可知

图2 俯仰角变化示意图Fig.2 Diagram of pitch angle change

考虑AUV 发生如图3 所示的姿态变化,即俯仰角为0°,横滚角从0°变为 ϕ,同理可知

图3 横滚角变化示意图Fig.3 Diagram of roll angle change

可见,式(3)和式(4)是在理想情况下得到的,然而实际运动工况中,受海洋湍流、运动噪声和测量误差等因素影响,直接利用上述公式计算得到的姿态参数难以实际使用,需要探索研究新的模型构建方法,利用压强与姿态间的基本函数关系建立具有鲁棒性的计算模型。

1.1 模型选取依据

人工神经网络是一种常见的建模数据间关系的方法[11]。其中,MLP 作为一种前馈神经网络,是人们对生物神经系统进行模拟、简化后得到的模型。由于其结构简单,对噪声鲁棒,因此在建模非线性数据时广泛应用[12]。为了模拟鱼类侧线系统对压强数据的处理方式,并且考虑到压强与姿态间存在非线性关系,因此采用MLP 建模压强与姿态间的函数关系。

1.2 模型结构

MLP 包括输入层、隐藏层和输出层三部分,图4为MLP 模型示意图。

图4 MLP 模型示意图Fig.4 Diagram of MLP model

输入层处理压力传感器阵列测量的压强数据;隐藏层使用双曲正切函数作为激活函数,实现对非线性函数的拟合[13];输出层为姿态信息,包括俯仰角和横滚角。使用均方误差(mean square error,MSE)作为损失函数RMSE,其计算公式为

式中:N为试验数据样本数量,每条试验数据包含某一时刻压力传感器阵列测量的压强数据和测姿设备测量的姿态数据;ypre和yreal分别为模型输出的预测值和AUV 姿态参考真值,这里将测姿设备测量记录的姿态视为AUV 姿态参考真值。在损失函数的基础上,利用梯度下降法完成模型参数更新[14]。

1.3 模型训练方法

复杂的水下环境会影响压力传感器测量结果,因此在数据输入MLP 模型前,需要对压力传感器测量数据进行降噪处理。采用卡尔曼滤波方法对数据进行降噪[15-16]。首先给出离散形式的状态模型和观测模型,即

式中:xk为系统第k步时的状态;yk为第k步时的观测数据;qk-1为第k-1步时的过程噪声,且qk-1～N(0,Qk-1);rk为第k步时的观测噪声,且rk～N(0,Rk);Ak-1为状态转移矩阵;Hk为观测矩阵,初始状态x0～N(m0,P0)。计算公式为

将m0设为y0,即初始状态均值是观测数据的首个值,并设P0为0.001 kPa2,即可利用式(13)～(17)和观测数据估计出状态信息。图5 中画出滤波前后的压强数据变化情况,可以看出,卡尔曼滤波算法成功去除了原始数据中的噪声。

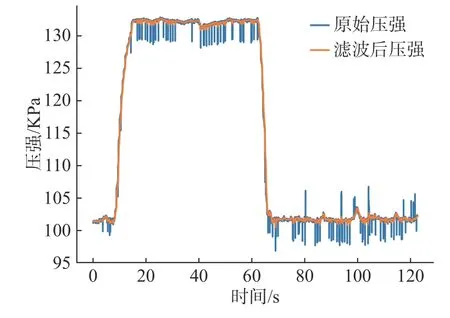
图5 滤波后压强对比图Fig.5 Pressure contrast diagram after filtering

其次,降噪后需对数据进行标准化处理。标准化公式为

式中:xj(i)为第j个压力传感器测量的第i条压强数据;E为均值;var为方差;M为压力传感器阵列的压力传感器个数。标准化操作可以消除数据数量级对模型的干扰,并加速模型收敛速度。

最后,MLP 模型中需要设置3 个超参数,分别是学习率(learning rate,LR)、迭代次数(Epoch)和批处理大小(Batch-size)。设定方法见2.2 节。

具体训练MLP 模型的方法如图6 所示,基本步骤如下:

图6 模型训练流程图Fig.6 Flowchart of model training

1)对试验数据进行预处理,包括数据降噪和标准化操作。

2)将试验数据随机划分为训练集、验证集两部分,占比分别为80%和20%。

3)将训练集、验证集的压强数据输入到MLP模型中,并利用姿态参考真值和模型输出的预测值分别计算训练集、验证集模型损失。

4)判断模型是否出现过拟合问题,如果验证集模型损失随训练次数增加而变大,说明发生过拟合,提前结束训练。

5)在训练集模型损失的基础上计算梯度。

6)按照设置的学习率,利用梯度下降法更新模型参数。

7)返回步骤3),直到训练次数达到设置的迭代次数。

2 外场试验与模型参数确定

2.1 外场试验

为验证模型的有效性,在陕西省咸阳市内的醴泉湖开展了外场试验,使用的测试载体是“天河二号”AUV,如图7 所示。“天河二号”AUV 是一款小型化、低成本AUV,其规格参数见表1。AUV上安装测姿设备、压力传感器阵列和全球定位系统(global positioning system,GPS)等传感器。压力传感器阵列包含16 个压力传感器,安装布局如图8 所示。

图7 “天河二号”AUVFig.7 Tianhe II AUV

表1 “天河二号”AUV 规格参数Table 1 Parameters of Tianhe II AUV

图8 压力传感器安装布局Fig.8 The layout of pressure sensors

测姿设备型号为HMR3500,误差为0.2°,采样率为10 Hz。压力传感器型号为MPM281VC,测量范围0～350 kPa,误差为0.7 kPa,采样率为1 000 Hz。由于姿态数据和压强数据采样率不同,需要进行数据对齐。具体方法是:先使用平均值池化操作(average-pooling)处理压强数据,将其采样率降低为10 Hz,再按照时间戳与姿态数据对齐。

为收集AUV 不同运动状态下的传感器数据,需要控制其完成多组试验任务,主要从轨迹、深度和速度3 个要素调整试验方案。轨迹包括直线形、割草机形和圆形,详见图9。深度包括2 m 和4 m,即控制AUV 分别在水下2 m 和4 m 完成3 种轨迹的航行。在不同轨迹、不同深度条件下,开展AUV 匀速航行试验。对直线形轨迹,设计加速和减速航行2 种试验方案。受AUV 控制能力所限,在开展直线形轨迹变速航行试验时,采取先匀速航行,再加速或减速航行,再匀速航行。试验详情见表2。

图9 AUV 航行轨迹示意图Fig.9 Diagram of AUV's track

表2 试验设置Table 2 Experimental setting

2.2 模型参数确定

使用表2 中第1～14 组试验数据训练MLP 模型 (按照1.3 节给出的数据划分方法将数据划分为训练集和验证集),使用第15～20 组试验数据作为测试集检验模型有效性。由于试验中压力传感器阵列包含16 个压力传感器,故将MLP 模型的输入层节点个数设为16。隐藏层节点个数通过对比试验确定,分别将隐藏层节点数设为8、16、32 和64,利用训练集数据训练模型,分别计算模型在训练集和验证集上的模型损失,结果见表3。从表3 中可以看出,隐藏层节点数越多,在训练集上可得到越好的预测结果,但节点64 的验证集模型损失大于节点32,且节点32、64 的验证集模型损失与训练集模型损失相差较大,判断节点数大于32 时可能存在过拟合现象。综合考虑模型复杂度、模型损失和过拟合现象,将隐藏层节点设为16。

表3 不同隐藏层节点数时模型损失Table 3 Loss of model with different hidden nodes

批处理大小设为N,即每次训练模型使用全部训练集数据。LR 分别设为0.000 1、0.000 2、0.000 5、0.001、0.002、0.005、0.01、0.02、0.05、0.1、0.2 和0.5,迭代次数设为1 000 000,每迭代500 次输出一次模型损失,图10 给出不同学习率时,随着迭代次数的增加,训练集模型损失的变化情况(学习率设为0.5 时出现梯度爆炸现象,模型无法收敛,因此图中未画出)。从图10 可以看出,当迭代次数大于200 000 时,利用不同学习率训练的模型在训练集上有着相近的收敛趋势,但学习率设为0.000 1、0.000 2、0.000 5、0.2 时,训练集模型损失较大。

图10 训练集模型损失示意图Fig.10 Diagram of loss of model on training set

为进一步对比LR 和Epoch,分别计算LR 为0.000 1、0.000 2、0.000 5、0.001、0.002、0.005、0.01、0.02、0.05、0.1、0.2,迭代次数为200 000、400 000、600 000、800 000 和1 000 000 时模型在验证集上的模型损失,计算结果见表4。可以看出,随着迭代次数的增加,模型损失越来越小,此外,随着LR 的增加,模型损失先变小后变大。分析其原因为,LR 过小时,模型参数更新缓慢,导致模型不收敛;LR 过大时,模型参数更新量过大引起梯度爆炸,导致模型不收敛。为得到最优模型,将LR设为0.01,迭代次数设为1 000 000。

表4 不同LR 和迭代次数时验证集模型损失Table 4 Loss of model on validation set with different LR and Epoch

3 结果及分析

图11～16 分别是使用第15～20 组试验数据得到的模型预测值和姿态参考真值,其中,蓝线为姿态参考真值,即测姿设备测量的姿态数据,黄线为模型输出的预测值,即利用压强数据预测的姿态。

图11 试验15 模型预测结果Fig.11 Model prediction result of experiment 15

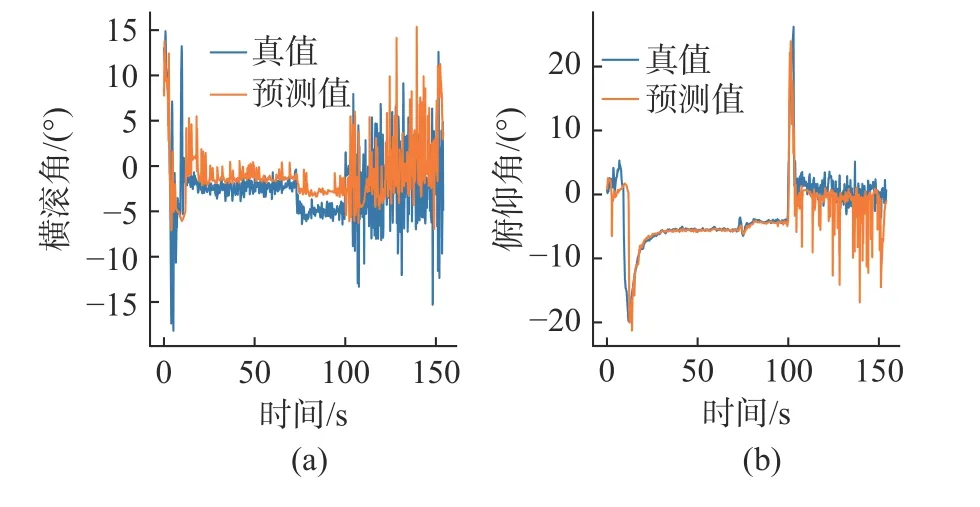
图12 试验16 模型预测结果Fig.12 Model prediction result of experiment 16

图13 试验17 模型预测结果Fig.13 Model prediction result of experiment 17

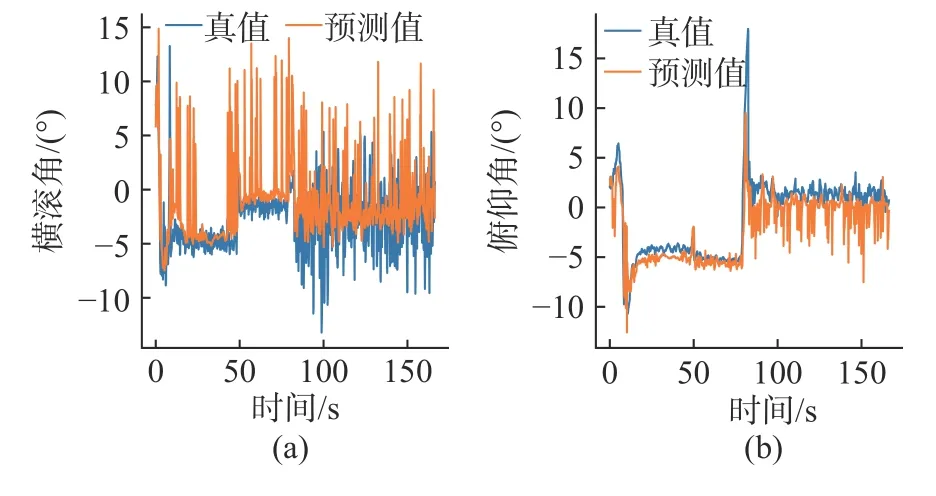
图14 试验18 模型预测结果Fig.14 Model prediction result of experiment 18

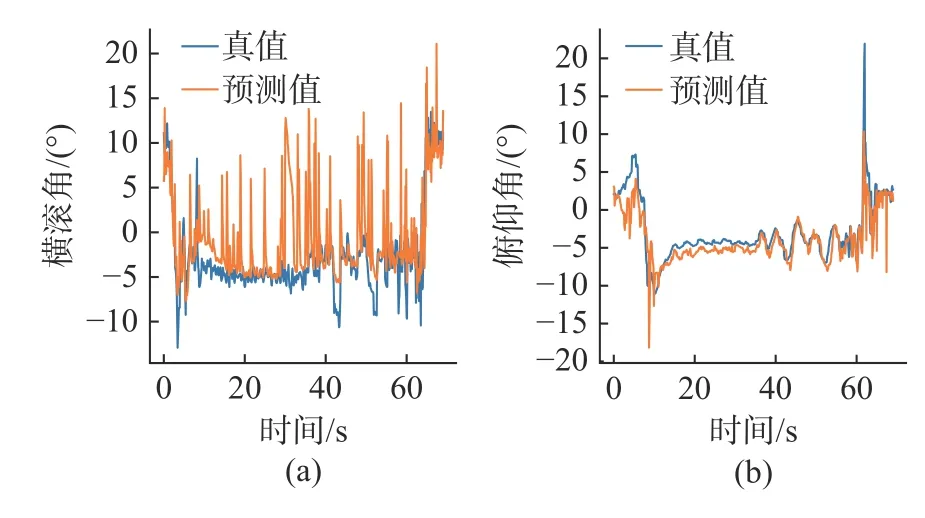
图15 试验19 模型预测结果Fig.15 Model prediction result of experiment 19

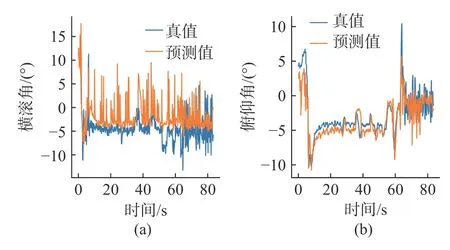
图16 试验20 模型预测结果Fig.16 Model prediction result of experiment 20

由图11～16 可知,俯仰角的预测精度优于横滚角,对此分析如下:从式(3)和式(4)可以看出,当压强数据出现干扰时,姿态误差受压力传感器之间的距离影响,由于试验所用AUV 的L＞D,所以俯仰角误差理论上小于横滚角误差,这在实际测试数据上也得到证实。此外,由图11 可以看出,当时间小于10 s 或大于90 s 时的预测误差明显大于当时间大于10 s 且小于90 s 时的预测误差(从图10～14 也可得出相同结果,但时间节点不同),对此分析如下:时间小于10 s 时,AUV 执行下潜操作,产生剧烈水流波动,干扰压力传感器测量数据,因此模型误差较大;时间大于90 s 时,AUV 执行上浮操作,同样产生剧烈水流波动,并且在AUV 上浮至水面后,一部分压力传感器未处于水下,导致压力传感器测量数据存在较大误差,因此模型误差较大;时间大于10 s 且小于90 s 时,AUV 在水下定深航行,水流相对平稳,因此误差较小。

为提高模型预测精度,当AUV 潜深大于一定数值时再利用模型输出预测值。使用均方根误差(root mean square error,RMSE)表示模型预测误差,对利用式(5)计算的结果再开根号即可得到RMSE。将AUV 深度阈值设为0.5 m,表5 给出了潜深阈值设定前后利用试验15～20 计算的横滚角和俯仰角RMSE,由表可知,设定后的模型预测精度得到提高。然而,从试验18～20 可以看出,设定后横滚角精度提升较小,甚至降低,对此分析如下:从图14～16 可以看出,试验18～20中AUV 水下定深航行时依然存在较大横滚角误差,因此设定后模型预测精度并未提升,推测误差来源为传感器测量误差,由于试验地点为景区,开展试验18～20 时有游客在试验水域附近划船,并且AUV 的下潜深度为2 m,易受游船产生的水流波动影响,因此压力传感器测量数据出现较大误差。

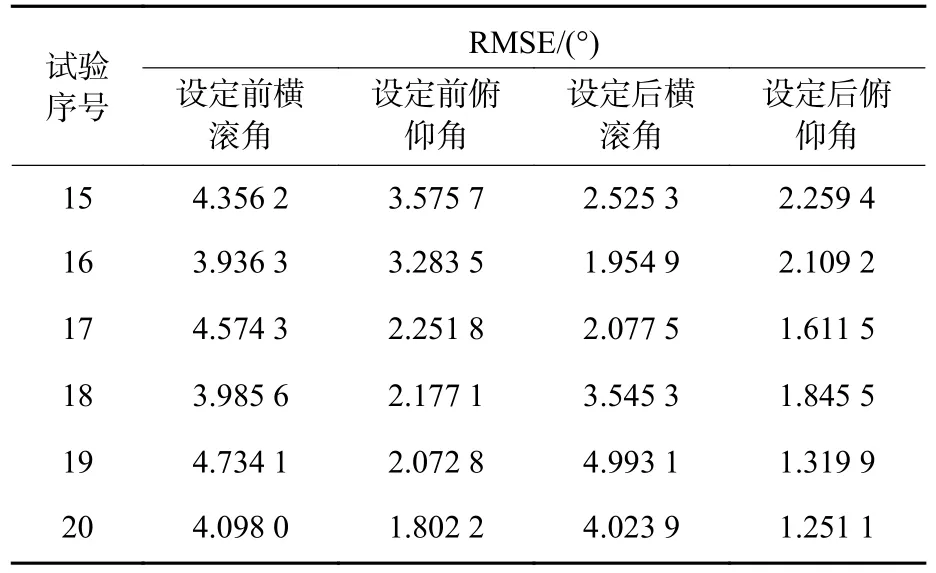
表5 不同条件下的RMSETable 5 RMSE with different conditions

将训练集的全部数据输入模型,当AUV 潜深大于0.5 m 时利用模型输出姿态预测值,并计算横滚角和俯仰角RMSE,得到模型的横滚角误差为2.990 8°、俯仰角误差2.069 9°。

4 结论

受仿生学研究启发,提出一种基于压力传感器阵列的姿态反演估计模型,并开展外场试验进行验证,得出以下结论:

1)模型的俯仰角预测精度优于横滚角,预测精度受压力传感器之间安装距离影响,安装距离越大,预测精度越高。

2)当AUV 浮于水面或离水面较近时,模型预测精度较低,实际应用中需设置潜深阈值,当AUV潜深大于阈值时再启用模型。

提出的基于压力传感器阵列的姿态反演估计模型适用于小型化、低成本AUV。实际应用中,首先在AUV 上安装高精度测姿设备和压力传感器阵列,并开展外场试验收集试验数据,然后利用数据训练模型,模型训练完毕后,将高精度测姿设备替换为低成本测姿设备,之后利用模型输出姿态预测值,为自主导航系统提供姿态矫正信息。由于利用压强数据和姿态反演估计模型得到的姿态信息不存在累积误差,因此该方法在自主导航系统中具有较高应用潜力,下一步工作将继续研究提高模型预测精度的方法。