柔性胸鳍推进仿蝠鲼机器鱼CPG 运动控制

南凯刚,姜 晟,张进华,成海炎

(西安交通大学 现代设计及转子轴承系统教育部重点实验室,陕西 西安,710049)

0 引言

自主水下航行器是海洋科技中的重要组成部分,在军、民领域均有广泛应用,涵盖情报收集、水下及水上侦查监视、作战打击和后勤支援等诸多领域,具有重要的军事价值,已成为世界各国海军装备的重要研究方向。海洋中的鱼类生物经过长期的自然进化,为了获得快速躲避天敌、捕食等能力,进化出了各具特色的水中推进模式,展现出优秀的游动性能[1],具有推进效率高、机动性强、噪音低和环保性好的特点,成为自主水下航行器的理想仿生对象。因此,仿生机器鱼的研究成为智能水下机器人的一个前沿方向和研究热点,为研制新型的自主水下航行器提供了一种新途径。

根据不同的推进机理,Breder 等[2]于1926 年将鱼类推进模式分为身体/尾鳍推进模式与中央/对鳍推进模式2 类。随后学者们针对这2 类推进方式的游动机理展开了研究,为仿生机器鱼的研制提供了重要的理论基础[3]。利用身体/尾鳍推进模式的鱼类通常具有狭窄且灵活的身体,主要借助鱼类尾鳍和鱼身后半段摆动产生推进力[4],而中央/对鳍推进模式主要靠鱼类背鳍、胸鳍和腹鳍等多种柔性鳍产生推进力。相比之下,采用中央/对鳍推进模式的仿生水下航行器[5]虽然游动速度不快,但其宽大的胸鳍外侧在游动时展现出明显的柔性大变形和相位延时[6-7]。这些形状特征和运动特点使得中央/对鳍推进模式的鱼类具有高效而平稳的巡游能力,采用中央/对鳍推进模式的仿生水下航行器更适合于对侦查环境机动性要求较高的场合[8]。

在经历了近半个世纪的摸索与研究之后,采用胸鳍拍动推进方式的仿生机器鱼研究工作取得了长足发展。近年来,研究者和工程师模仿蝠鲼完成了多种不同的仿蝠鲼机器鱼设计。Zhou 等[9]研究了蝠鲼的胸鳍拍动和水中滑行规律,研制并改进了仿蝠鲼机器鱼Roman-Ⅱ,原型样机的最大游动速度为0.85 BL/s(体长/秒)。李吉等[10]仿照蝠鲼的胸鳍拍动规律研制出仿蝠鲼机器鱼BH-RAY3,该样机采用双侧刚性胸鳍前缘的拍动和柔性胸鳍的被动变形进行运动,最大游动速度为1.10 BL/s。Gao 等[11]结合蝠鲼胸鳍的骨骼结构和运动特征,设计出具有一对柔性硅胶胸鳍的仿蝠鲼机器鱼,最大航速为1.4 BL/s。Chew 等[12]分析了蝠鲼的运动机理并设计了仿蝠鲼胸鳍推进的机器鱼MantaDroid,经测试该原型样机游动速度最高可达1.78 BL/s。总结近年来国内外仿蝠鲼机器鱼研究现状,其研究焦点逐渐从刚性鳍驱动转换到了柔性鳍驱动,逐步实现了从机器鱼本体外形相似转化到胸鳍运动变形规律相似,基本能完成直线游动等简单运动,但其机动性能仍与真实的鱼类相差甚远,严重限制了它们在实践中的应用。

仿生机器鱼的游动过程伴随着鱼体多个自由度的协调运动控制以及不同运动模式间的相互切换。机器鱼在水下的工作环境复杂难测,为保证机器鱼在水下可以准确、高效地完成任务[13],在实际的运动控制中,需要设计实时稳定的控制策略以保证仿生机器鱼驱动器的多自由度协调控制。基于中枢模式发生器(central pattern generators,CPG)的底层控制方法能有效地模拟生物低级神经中枢自发产生的节律运动[14],在协调多自由度运动方面具备优良特性。近年来,CPG 已经越来越多地应用于仿生机器人的运动控制上。现有研究中,根据CPG 产生的控制信号原理的不同,可将CPG模型划分为基于神经元的模型与基于非线性振荡器的模型2 类。其中基于非线性振荡器的模型,例如Ijspeert 相位振荡器和Hopf 谐波振荡器等具有控制参数较少、模型结构简单、运算量较小以及易于实现的优点,仅需少量控制参数就能实现机器人复杂节律运动的控制,在协调机器人多自由度运动方面具有一定的优越性。在确保能够输出稳定的周期性振荡信号的前提下,形式简单、参数较少、计算量小、便于分析、易于实现的CPG 模型是更好的选择。

Shi 等[15]提出了一种基于CPG 的运动控制模型,实现了机器鱼的不同运动模态切换。汪明等[16]针对胸鳍推进型仿生鱼的游动特点,提出了一种幅度与频率均可独立控制的非线性神经元振荡器模型,并在此基础上完成了仿生机器鱼的直线巡游、倒游和转弯等模式的运动控制以及上述运动模式间的相互切换。Zhou 等[17]采用同样类型的CPG 控制方法,实现了对多电机并联的波动胸鳍的运动控制。虽然上述CPG 控制方法具有诸多优良特征,但是目前仍有一些问题尚待解决。大多数CPG 模型表达式具有非线性与高维数的特点,控制参数与输出特征并非一一对应,这给系统的参数调整以及后期与闭环控制算法的结合造成了一定的困难。

尽管现有的拍动式仿生机器鱼能实现包括直线游动与定深巡游在内的简单运动功能,但其在游动稳定性与机动性上仍存在一定的不足。因此,文中采用蝠鲼为仿生对象,利用仿生学设计思想,以蝠鲼柔性胸鳍的形态学特征及解剖学特点为切入点,建立基于辐骨关节的柔性胸鳍运动学方程,用以描述柔性胸鳍拍动时复杂的空间曲面变形规律。然后基于上述对仿生对象胸鳍的形态学和解剖学的研究,提出了仿生柔性胸鳍设计,并根据机器鱼的功能仿生需求,完成了机器鱼的结构设计。同时针对上述CPG 控制方法存在的问题,在原有Ijspeert模型[18]的基础上,提出了一种线性的相位振荡器模型,用以控制仿蝠鲼机器鱼的运动,实现仿生机器鱼直线巡游、左右转弯及浮潜等运动模式。通过一系列游动性能测试验证,文中设计的仿蝠鲼机器鱼具有较好的机动性能,其最大游动速度为1.9 BL/s,同国内外同类型仿蝠鲼机器鱼相比,展现出较好的优越性。

1 仿蝠鲼机器鱼设计方案

1.1 蝠鲼运动特征分析

蝠鲼作为采用拍动推进模式鱼类的典型代表,拥有扁平宽大的三角形中央对鳍,鱼体呈现良好的流体动力外形。图1 展示了蝠鲼转向、下潜及直线巡游时的图像序列[19]。当蝠鲼直线巡游时,其身体躯干部分基本维持刚性不动,运动部分主要集中于两侧的胸鳍部分。转向时伴随着两侧胸鳍的异步拍动,产生转向所需的力矩,从而实现游动方向的调整。在整个拍动过程中,胸鳍以身体中性面为基准上下同步拍动,由鱼体中性面向上拍动的幅度约为向下拍动幅度的2 倍。蝠鲼在不同的运动步态下,其胸鳍表面均呈现出较复杂的曲面变形,蝠鲼胸鳍运动规律可近似等效为沿翼展与体长2 个方向振幅递减的正弦波,且沿弦长方向正弦波的波数一般小于0.4 个。

图1 蝠鲼在不同运动姿态下的形态特征Fig.1 Morphological characteristics of different moving postures for manta ray

蝠鲼优异的运动表现很大程度上取决于胸鳍灵活多变的柔性变形。蝠鲼依靠胸鳍柔性变形产生的矢量合力,能实现多自由度的灵活运动。根据蝠鲼运动形态特征,蝠鲼游动时胸鳍中辐骨并不是同时被激活,而是由前往后以一定的相位差依次激活,以实现鳍面上类似于正弦波的推进波传递,利用其胸鳍的被动自由度与运动姿态的协调控制来提高其机动性。在设计机器鱼时借鉴蝠鲼胸鳍的外形特征,同时也要便于实现和控制,以提升机器鱼本体的水下稳定性和机动性。

1.2 设计方案

根据仿生学设计方法,基于蝠鲼的生物学特点,结合功能仿生需求,提出了一种通过中央对鳍与尾鳍相互“耦合”协调驱动实现水中多自由度矢量推进的仿蝠鲼机器鱼设计方案,如图2 所示。

图2 仿蝠鲼机器鱼整体设计方案Fig.2 Overall design scheme of the bionic manta ray robotic fish

如图2(a)所示,机器鱼在尺寸上与幼年蝠鲼接近,长度为385 cm,翼展为500 cm;胸鳍弦向长度与展向长度分别为200 mm 和220 mm,展弦比为2.2。其硬件系统组成如图2(b)所示,系统主要由运动控制板、舵机组、数据通信模块、姿态感知模块以及供电模块等部分组成。整体结构采用模块化的设计理念,具有较高的功能适应性。仿蝠鲼机器鱼整体结构可分为4 个部分:头部舱段、中部电子舱、仿生尾鳍和1 对仿生胸鳍。机器鱼头部舱段整体呈三角锥状以降低游动时的流体阻力。头部舱段侧面的槽口用来固定2 个为仿生胸鳍提供动力的驱动舵机。具有真实蝠鲼躯干所呈现出的流线型和侧扁型特征的机器鱼中部电子舱作为驱动系统和电子设备的承载平台,能有效隔绝外部环境干扰,保证工作的稳定性。尾鳍的作用类似于飞机的水平尾翼,能通过垂直旋转调节机器鱼俯仰姿态。

柔性仿生胸鳍的结构示意图如图2(c)所示,其结构包括柔性鳍面与柔性鳍条。将胸鳍的前缘鳍条作为驱动源,带动整个柔性胸鳍周期性的摆动,鳍面与鳍条连接,模拟仿生对象的柔性辐骨与肌肉结构,充分利用鳍条与鳍面的被动自由度,以实现仿生胸鳍的高机动性推进。3 根鳍条沿体长方向横置排列,其中驱动鳍条与体长方向夹角为80°。仿生胸鳍的驱动鳍条采用非均匀刚度分布设计,厚度由根部过渡至端部逐渐递减,保证了拍动时仿生胸鳍端部位置的大幅被动变形。整个柔性仿生胸鳍通过位于前缘的驱动鳍条往复摆动,被动地驱动整个胸鳍。3 根鳍条均采用柔性较好的高韧性尼龙(PA12)材料通过激光烧结技术制造,鳍面材料选取柔性硅橡胶制作。单侧胸鳍由一个与驱动鳍条相连接的高性能防水舵机驱动。仿生胸鳍与舱体部分通过柔性铰链连接,易于拆卸与安装。安装好的仿蝠鲼机器鱼样机如图2(d)所示,总质量约为720 g。

2 仿蝠鲼机器鱼CPG 运动控制

自然界中,蝠鲼通过如图3 所示的形式协调两侧胸鳍的周期性摆动,频繁地切换运动步态,实现低速游动时的高机动性。因此在实际的运动控制中,需要设计实时稳定的运动控制策略,以保证仿生机器鱼驱动器的多自由度协调控制。CPG控制方法通常由数个中枢神经单元组成,能利用神经单元之间的相互抑制或激活,形成稳定的节律信号。此外,在完成不同运动模式间的切换时,基于CPG 仿生控制系统能通过系统中的神经元之间的耦合作用,自发地产生平稳的相位关系,做到仿生机器鱼本体不同游动模式之间的平稳过渡。

图3 蝠鲼游动时胸鳍的协同配合Fig.3 Synergy of pectoral fins during manta ray swimming

2.1 CPG 控制算法设计

考虑到CPG 能产生节律性运动的特点,结合机器鱼仿生胸鳍的游动特点,使用简化后的相位振荡器作为CPG 拓扑网络的基本组成单元,其模型动态特性的数学表达式为

式中:ai、bi和xi为方程中的状态变量,分别为第i个振荡器当前的幅度、偏移量与相位;i=1,2,3 分别为与仿蝠鲼机器鱼左侧舵机、右侧舵机和尾部舵机相对应的相位振荡器;Ai与Bi分别为第i个振荡器的期望幅度与期望偏移量;αi与βi分别为幅值与偏移量的收敛系数,决定了方程中状态量ai和bi收敛至期望值的速度;fi为振荡器产生节律信号的频率;µij为第i个振荡器与第j个振荡器之间的耦合系数,决定了对应振荡器之间的耦合强弱;φij为第i个振荡器与第j个振荡器之间的锁θi存相位差;θi为第i个相位振荡器最终输出的舵机角度。

仿蝠鲼机器鱼的驱动结构主要由左右仿生胸鳍和1 个尾鳍所组成,针对机器鱼3 个驱动器的3 个自由度,设计了如图4 所示的3 个相位振荡器组成的CPG 拓扑网络。

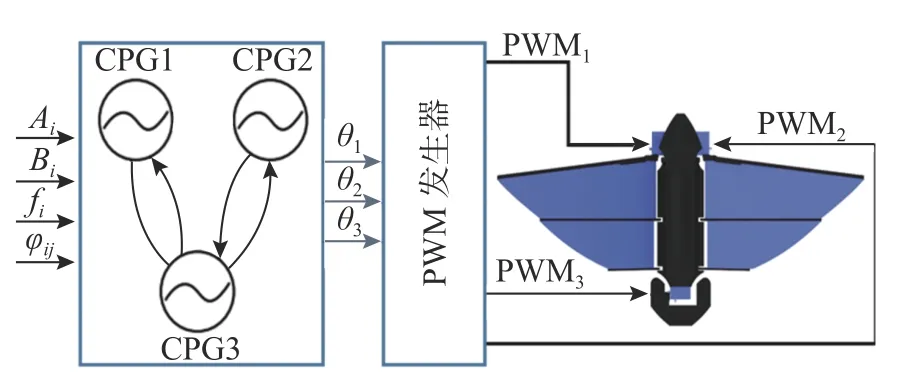
图4 机器鱼CPG 控制结构示意图Fig.4 Schematic diagram of CPG control structure for robotic fish

图中:3 个相位振荡器仅与其相邻振荡器相耦合,降低了模型中耦合参数的数量,减轻了模型的计算难度;fi、Ai、Bi与φij为影响模型输出信号的4 个输入控制信号;θ1、θ2与θ3作为CPG 网络拓扑结构的输出量,经脉宽调制(pulse width modulation,PWM)发生器映射后转化为对应的PWM 信号,控制舵机摆动至指定角度,从而实现对相关机器鱼柔性胸鳍或尾鳍的驱动频率、拍动幅度、偏移量和相位差的控制。通过调节输入控制参数及收敛因子的大小,方程能够产生不同幅值和相位的耦合驱动控制信号,控制仿生机器鱼完成不同运动模式的平稳切换。为便于计算,离散的CPG 方程为

在应用CPG 控制方法时,首先确定fi、Ai、Bi和φij这4 个输入控制参数,设置耦合系数µij以及收敛因子αi与βi的数值,以及一次方程中状态变量ai、bi和xi的初始迭代数值。完成初值设置后,间隔固定时间(20 ms)对CPG 离散方程进行迭代求解。

2.2 CPG 拓扑网络控制参数影响规律

采用控制变量法,观察控制参数对CPG 拓扑网络输出信号的影响。在仿真过程中,令相位振荡器之间耦合系数µij=1;幅值收敛因子αi=1;偏移量收敛因子βi=1;状态变量ai、bi和xi的初始迭代数值均设置为0。

1)频率控制参数对输出信号的影响

当t=4 s 时,输入频率控制参数从1 Hz 突变至2 Hz,CPG 拓扑网络输出信号的变化情况如图5所示,其中参数φij、Ai和Bi(i=1,2,3)的取值分别为2 rad、60°和0。由图5 可知,在频率控制参数fi由1 Hz 增加至2 Hz 后,CPG 控制信号周期减小频率增大,因此通过对频率控制参数的调节可以实现对CPG 输出信号中频率的控制。此外,通过突变前后CPG 输出信号发现,信号的幅值与相位没有发生明显突变。因此,CPG 拓扑网络在响应频率控制参数的变化时,输出信号的平滑性良好。

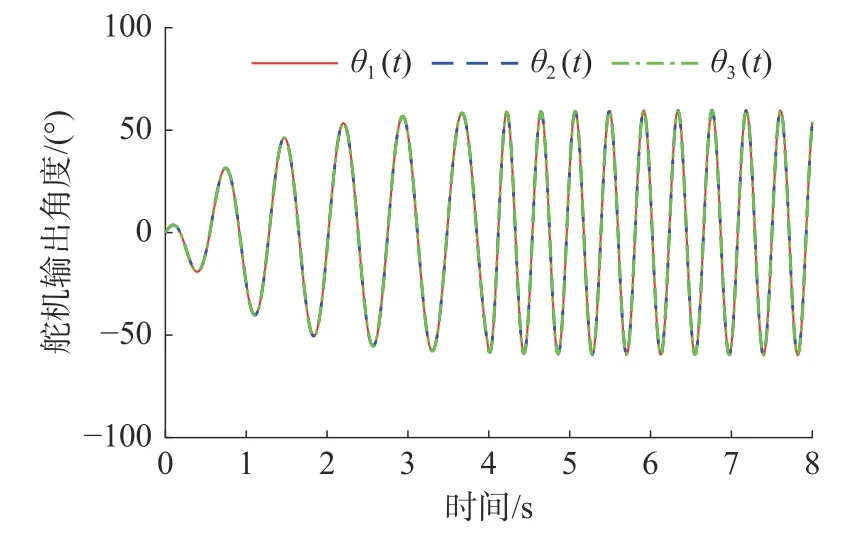
图5 频率控制参数fi 突变对CPG 输出信号的影响Fig.5 Influence of frequency control parameter fi mutation on CPG output signals

2)相位差控制参数对输出信号的影响

在相位差控制参数φij发生突变时(t=4 s),CPG的输出信号如图6 所示。由图6 可知,当相位差控制参数φij为0 时,相位振荡器CPG1～CPG3 输出的信号始终保持同步,而当φij从0 增加至2 rad时,CPG 拓扑网络输出的信号间开始出现相位差,因此调节参数φij可以实现对CPG 输出信号间相位差的调节。

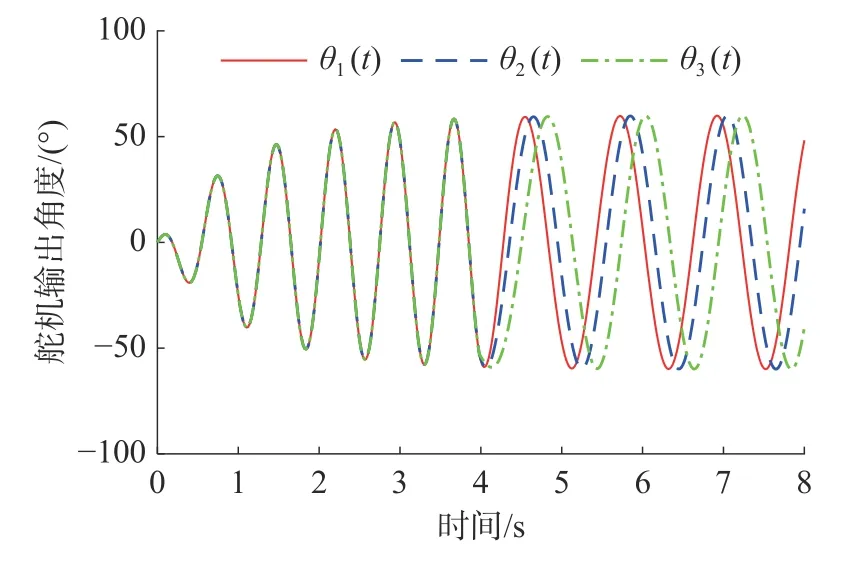
图6 相位差φij 对CPG 输出信号的影响Fig.6 Influence of phase difference φij on CPG output signals

3)幅值控制参数对输出信号的影响

在幅值控制参数Ai发生突变时(t=4 s),CPG 的输出信号如图7 所示,其中参数fi=1 Hz、φij=0、Bi=0。由图可知,CPG 拓扑网络输出信号的幅值随控制参数的突变而平缓增大到指定值,因此,CPG 拓扑网络在响应参数Ai的变化时,输出节律信号的平滑性良好。

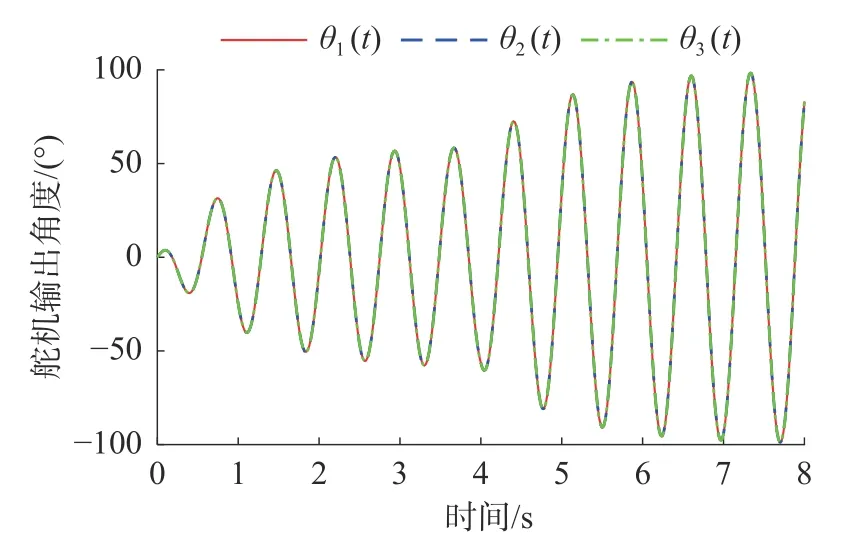
图7 幅值控制参数Ai 对CPG 输出信号的影响Fig.7 Influence of amplitude control parameter Ai on CPG output signals

4)偏移量控制参数对输出信号的影响

当偏移量控制参数Bi分别为20°和－20°时,CPG 拓扑网络结构输出信号如图8 所示,其中参数fi=1 Hz、φij=0、Ai=60°。由图8(a)可知控制参数Bi为正时,CPG 控制信号的平衡状态整体向上移动;由图8(b)可知Bi为负时,CPG 控制信号的平衡状态整体向下移动。因此,调节控制参数Bi的大小可以控制CPG 输出信号的偏移量大小。

图8 偏移量控制参数Bi 对CPG 输出信号的影响Fig.8 The influence of deviation control parameter Bi on CPG output signals

5)收敛因子对输出信号的影响

为了实现机器鱼运动模式的平稳和快速转换,可以通过调节收敛因子αi与βi使CPG 拓扑网络中的状态量收敛至期望值,进而减小输出信号的过渡时间。文中增加了收敛系数的对比仿真结果,如图9 所示。

图9 展示了当拍动幅值从60°过渡到80°时,不同收敛因子对应的CPG 输出信号。当收敛因子αi与βi都设置为0.5 时,CPG 拓扑网络结构输出信号如图9(a)所示,约过4 s 才收敛到期望的幅值;当设置收敛因子αi与βi都为5,CPG 拓扑网络结构输出信号如图9(b)所示,可知CPG 拓扑网络的输出信号在1 s 内便调整到了期望幅值,验证了通过调整收敛系数可以减小CPG 拓扑网络输出量的过渡时间的有效性,通过调节收敛因子可以调整运动模式转换的过渡时间,以适应机器鱼不同游动模式下的机动性要求。

3 仿蝠鲼机器鱼游动性能测试

自然环境中蝠鲼主要的游动模式包括直线定常巡游、转弯机动以及上浮下潜游动等。根据机器鱼各游动模式下的运动特征,通过对控制参数的调整进而调节机器鱼各舵机的工作频率和幅值以满足游动条件。文中针对仿生机器鱼在上述运动模式下CPG 拓扑网络输出的控制信号特征,对仿蝠鲼机器鱼进行游动性能测试,验证设计方案和CPG 拓扑网络运动控制策略的有效性。在测试中,令相位振荡器之间耦合系数µij=1;幅值收敛因子αi=1;偏移量收敛因子βi=1;状态变量ai、bi和xi的初始迭代数值均设置为0。

3.1 直线巡游模式

胸鳍拍动时除产生推进力与侧向力外,同时还将产生较大的升力[20]。由于产生的升力并不经过仿生机器鱼的质心,将会形成垂直于x-y平面的升力矩。当机器鱼实现直线定常巡游时,需要使重心所构成的力矩之和为零,处于如图10 所示的力矩平衡状态,才能完成直线定常巡游运动模式。

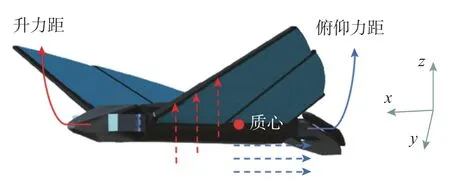
图10 机器鱼直线巡游时x-y 平面内所受力矩示意图Fig.10 The schematic diagram of the torque in the x-y plane during the straight line cruise of the robotic fish

因此,在直线巡游模式下,机器鱼需通过左右胸鳍的同步运动实现直线游动,并且通过尾鳍进行俯仰力矩的平衡调节,所以机器鱼左右胸鳍所对应CPG 相位振荡器的控制参数需保持一致,并且通过调整尾鳍CPG 相位振荡器的幅值控制参数使其保持平衡,实现机器鱼的直线巡游。当机器鱼处于直线巡游时,CPG 拓扑网络中各参数取值见表1。

表1 直线巡游模式下CPG 拓扑网络参数取值Table 1 Parameter value of CPG topological network in linear cruise mode

通过分析图11(a)各CPG 单元的输出信号θ1、θ2与θ3特征可知,在完成直线巡游运动模式时,机器鱼胸鳍与尾鳍均以相同频率同步摆动,以保持力矩平衡状态。尾鳍摆动幅值k可根据位姿传感器和深度传感器反馈的深度信息进行调节。通过图11(b)所示的直线巡游测试图像序列分析机器鱼的游动轨迹可知,机器鱼基本上可以稳定地沿直线游动,其平均游动速度为0.73 m/s,约为1.9 BL/s。如表2 所示,文中机器鱼的游动速度同国内外几款同类型仿蝠鲼机器鱼相比,展现出了较好的优越性。因此机器鱼在CPG 拓扑网络下,能较好地完成直线巡游任务。

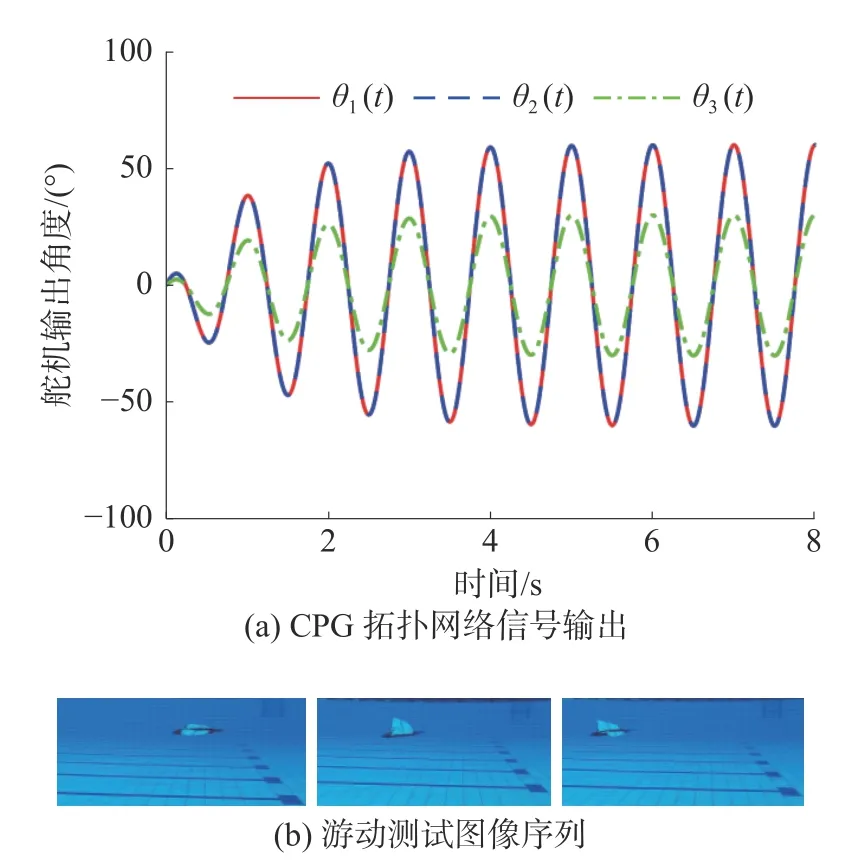
图11 机器鱼直线巡游模式下CPG 拓扑网络信号输出及其游动测试序列Fig.11 The signal output of CPG topological network and its swimming test sequence under the linear cruise mode of the robotic fish

表2 同类型仿蝠鲼机器鱼对比Table 2 Comparison of same type biomic manta ray robotic fish

受限于传感器等实验条件,暂未能展示机器鱼直线巡游过程中z轴方向的位移变化。但在实验观察中发现机器鱼存在z轴方向位移波动,这种现象是由机器鱼在游动中受自身及环境的实时干扰,而固定的CPG 控制参数不能实现实时的机器鱼俯仰力矩的平衡调节而导致。因此,在未来的研究工作中,也将考虑增加姿态传感器并设计基于俯仰角的闭环CPG 控制以实现仿蝠鲼机器鱼更平稳的直线巡游。

3.2 转向模式

机器鱼在水中采用转向模式实现转弯机动动作时,需通过左右胸鳍的差速摆动产生偏航力矩,从而改变机器鱼的游动方向,因此可调节机器鱼左右胸鳍对应的CPG 相位振荡器的频率控制参数使左右胸鳍实现差速拍动。即,仅需通过调整参数fi的大小,使CPG1 与CPG2 输出异步节律信号。当机器鱼处于转向模式时,CPG 拓扑网络中各控制参数取值见表3。CPG 拓扑网络信号输出仿真结果如图12(a)所示。机器鱼左侧胸鳍与右侧胸鳍的拍动频率之间存在差值,机器鱼依靠左右两侧胸鳍拍动产生的合力矩,调整偏航角度。其转向测试图像序列如图12(b)所示。

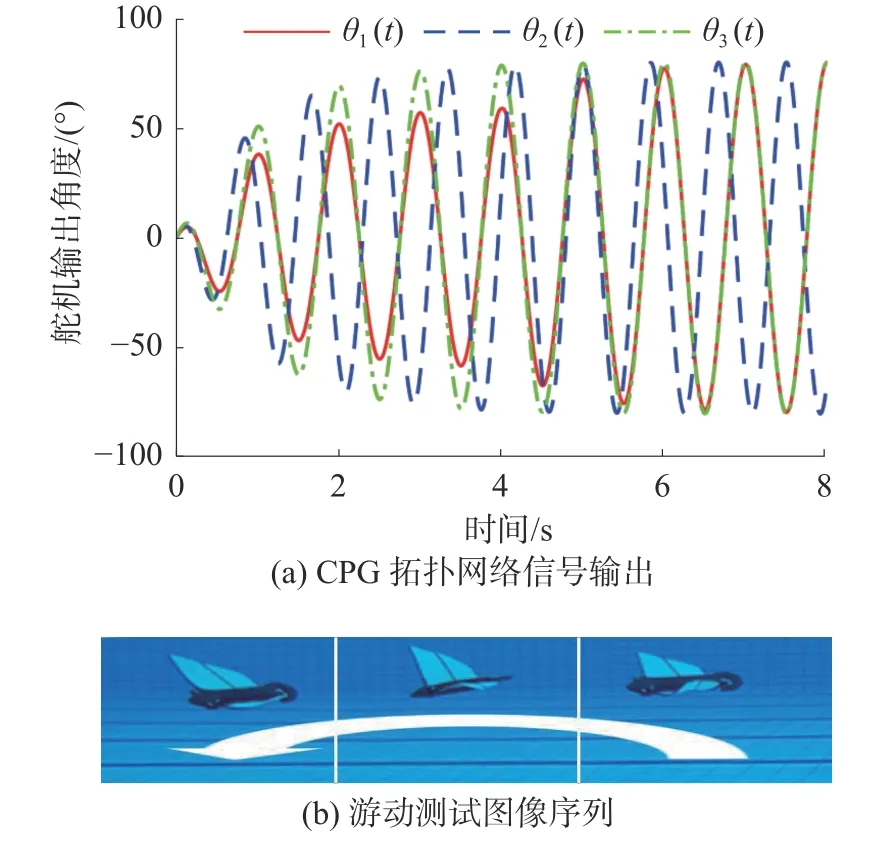
图12 机器鱼转向游动模式下CPG 拓扑网络信号输出及其游动测试序列Fig.12 The signal output of CPG topological network and its swimming test sequence under the steering mode of the robotic fish

表3 转向模式下CPG 拓扑网络参数取值Table 3 Parameter value of CPG topological network in steering mode

3.3 原地旋转模式

当机器鱼执行原地旋转游动步态时,左侧胸鳍与机器鱼本体中性面保持平行;右侧胸鳍则以较高频率拍动,机器鱼依靠右侧胸鳍产生的偏航力矩调整偏航角度,灵活机动地实现原地旋转动作。将表4 中参数输入CPG 离散方程后,得到的CPG 拓扑网络信号输出仿真结果如图13(a)所示,其原地旋转测试图像序列如图13(b)所示。

表4 原地旋转模式下CPG 拓扑网络参数取值Table 4 Parameter value of CPG topological network in local rotation mode

图13 机器鱼原地旋转模式下CPG 拓扑网络信号输出及其游动测试序列Fig.13 The signal output of CPG topological network and its swimming test sequence under the local rotation mode of the robotic fish

3.4 浮潜游动模式

机器鱼在水中完成上浮或下潜时,需使尾舵中性面的位置向上或向下偏移一定角度,通过尾舵产生的俯仰力矩控制俯仰角,实现机器鱼的浮潜运动,因此可调节尾鳍CPG 相位振荡器的偏移量控制参数进而控制机器鱼游动时的俯仰姿态角,从而实现机器鱼的上浮或下潜游动模式。CPG 中fi、φij和Ai3 个输入控制参数均保持不变,仅需通过调整参数Bi的大小,使尾舵中性面的位置向上或向下偏移一定角度,通过尾舵产生的俯仰力矩控制俯仰角,实现机器鱼的浮潜运动。

根据表5 中机器鱼浮潜游动模式下CPG 拓扑网络参数取值,得到如图14 的CPG 拓扑网络信号输出仿真结果。图14(a)和(b)分别为当机器鱼执行上浮和下潜的输出仿真结果及其游动步态测试序列。机器鱼在通过两侧胸鳍的同步拍动为机器鱼提供游动所需推进力的同时,调整尾舵摆动时中性面的位置,以控制机器鱼游动时的俯仰姿态角,从而实现机器鱼的上浮或下潜游动模式。

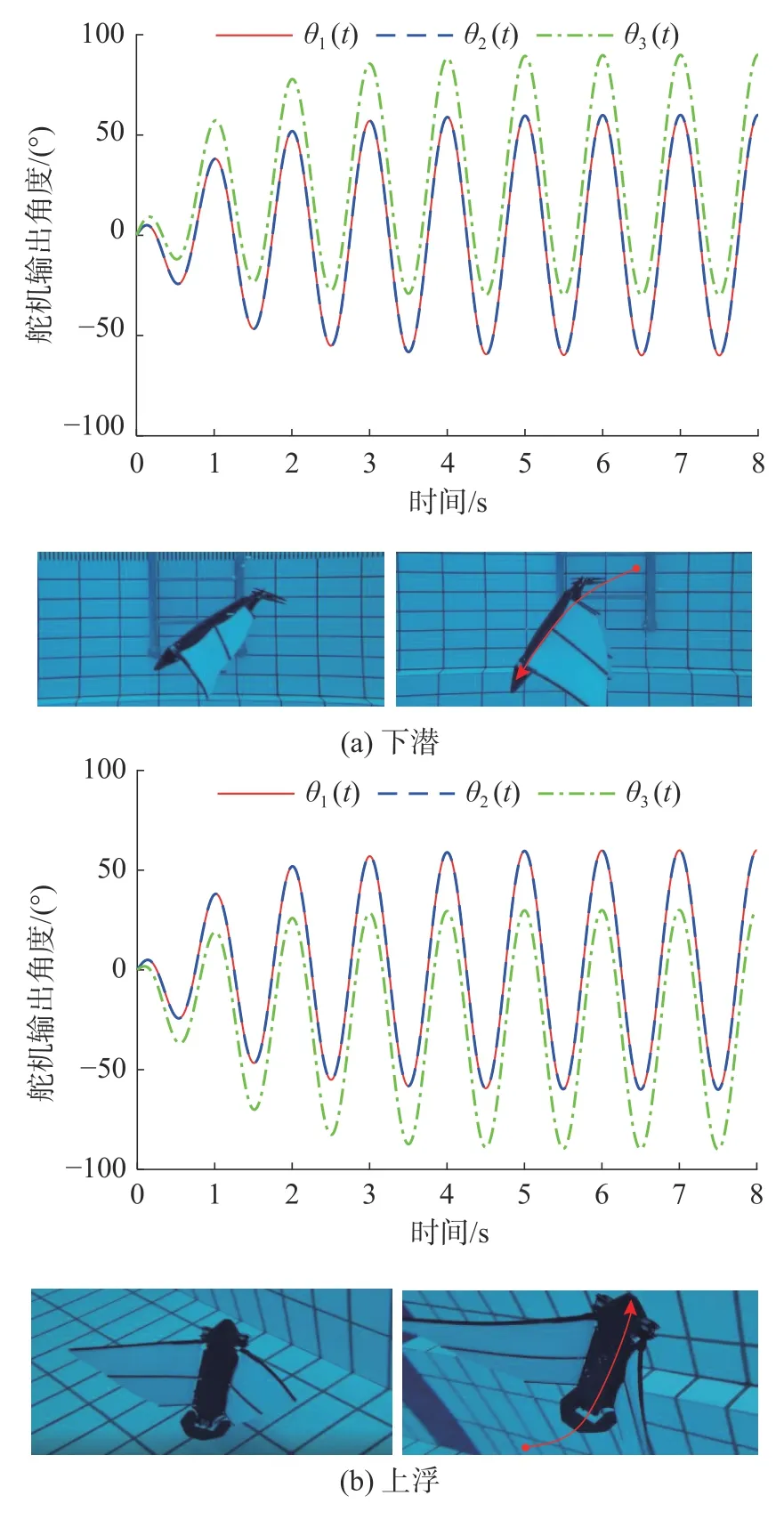
图14 机器鱼浮潜游动模式下CPG 拓扑网络信号输出及其游动测试序列Fig.14 The signal output of CPG topological network and its swimming test sequence under the floating and diving modes of the robotic fish

表5 浮潜游动模式下CPG 拓扑网络参数取值Table 5 Parameter value of CPG topological network in floating and diving motion mode

3.5 机动性能测试

为进一步验证仿蝠鲼机器鱼能否满足复杂动作机动性和功能仿生需求,模仿真实蝠鲼的优异运动本领,对仿蝠鲼机器鱼的机动性进行了如图15 所示的测试。

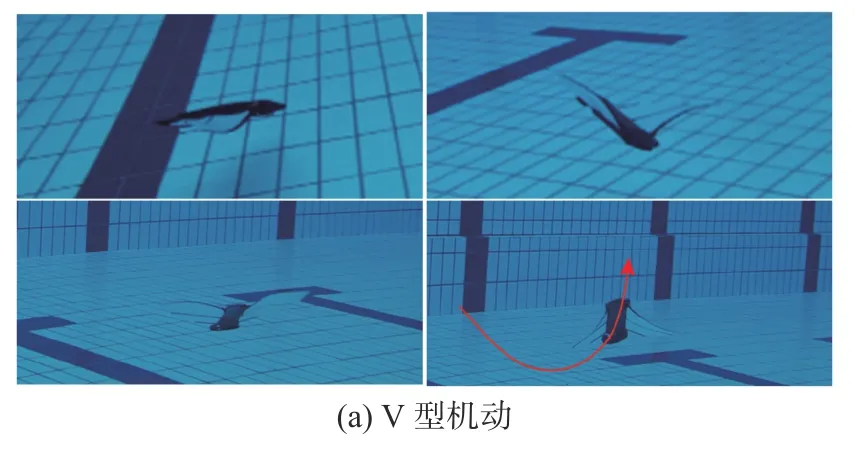
图15 机器鱼机动性能测试Fig.15 Mobility test of robotic fish

图15(a)中展示了仿蝠鲼机器鱼进行侧V 型机动时的运动图像序列。在游动过程中,胸鳍最大拍幅始终保持80°,左侧胸鳍拍动频率为0.7 Hz,右侧胸鳍拍动频率为0.5 Hz。通过对机器鱼左右胸鳍的差速控制,提升一侧胸鳍所产生的升力与推进力,为机器鱼本体提供横滚与偏航力矩。另一方面,通过调整尾舵的升降幅度,为机器鱼本体提供俯仰力矩。V 型机动模拟了真实蝠鲼捕捉猎物时的运动状态,在执行特定目标水域环境探测以及样本收集任务中具有潜在应用价值。图15(b)中展示了机器鱼完成横滚盘旋机动时的运动图像序列,整个过程可依次分为3 个阶段:加速爬升、横滚和盘旋。首先,机器鱼通过同步拍动两侧胸鳍,加速爬升至一定深度,随后加快左侧胸鳍拍动速度使其本体向右弦倾斜,最后协调两侧胸鳍同步慢速拍动以实现平稳的盘旋动作。在本次实验中机器鱼水中盘旋半径约为0.5 m,展现出了较好的机动性。横滚盘旋机动模拟了真实蝠鲼搜寻猎物时的运动状态,可用于执行对特定目标的持续监侦查任务。图15(c)中展示了仿蝠鲼机器鱼进行下潜翻滚时的运动序列,从运动序列中可观察到,机器鱼在推进力与尾舵提供的俯仰力矩共同作用下,沿逆时针方向进行翻滚下潜。试验结果表明机器鱼在尾舵与胸鳍的配合下可以在水中实现大角度的翻滚。通过机器鱼的机动性能测试可知,文中设计的仿蝠鲼机器鱼设计方案和CPG 拓扑网络运动控制策略可稳定实现仿蝠鲼机器鱼多种敏捷的水下运动,在执行水下搜救、探测等任务中具有较大应用前景。

4 结束语

采用拍动推进模式的鱼类中具有优异的机动性和稳定性,因此模仿拍动推进的水下推进器设计成为研究的热点。文中以蝠鲼为仿生对象,围绕拍动推进机器鱼的结构设计、运动控制策略和游动性能测试3 个方面展开,首先完成了仿蝠鲼机器鱼的整体设计和样机制作,接着构建了CPG 拓扑网络,最后经游动测试验证,该CPG 控制器能有效产生仿蝠鲼机器鱼直线巡游、机动转弯以及上浮下潜时所需的驱动信号。经游动测试后发现,仿蝠鲼机器鱼样机在游动过程中能保持较好的动态稳定性和机动性,可完成多种复杂的水下运动,且其最高游动速度可达1.9 BL/s,同国内外同类型仿蝠鲼机器鱼相比展现出较好的优越性。在未来的研究工作中,将考虑增加所设计仿生机器鱼的传感功能,并对文中所设计控制方法的响应特性和性能进行实验验证。