机器鳕鱼胸鳍/尾鳍协同推进直线游动动力学建模与实验研究
李宗刚,徐卫强,王文博,杜亚江
(兰州交通大学 机电工程学院,兰州 730070)
机器鳕鱼胸鳍/尾鳍协同推进直线游动动力学建模与实验研究
李宗刚,徐卫强,王文博,杜亚江
(兰州交通大学 机电工程学院,兰州 730070)
设计了一种二自由度胸鳍/尾鳍协同推进的仿生机器鳕鱼,其胸鳍推进机构不仅能够单独实现前后拍翼运动、摇翼运动以及两者的复合运动,而且还可与尾鳍实现协同推进,进而分别建立了胸鳍单独推进、胸鳍/尾鳍协同推进时的水动力学模型。数值仿真及实验结果均表明,胸鳍复合运动与尾鳍协同推进时,仿生机器鱼游速最快,可达0.30 m/s,胸鳍摇翼运动推进时游速最低,仅为0.05 m/s,其他推进方式的游速介于二者之间,但均能够实现稳定的游动。与现有结果相比,所设计仿生机器鱼直线游动模态多样,稳定游速可选范围较宽,机动性较好。
仿生鳕鱼;二自由度胸鳍;尾鳍;协同推进;水动力学分析
0 引 言
近年来,针对身体/尾鳍(Body/Caudal Fin,BCF)以及中央鳍/对鳍(Median/Paried Fin,MPF)推进仿生机器鱼的研究取得了大量成果[1-4]。其中,在BCF仿生机器鱼研究中,人们相继提出了细长体、二维波动板、三维波动板等游动动力学模型[5-6],并在变阻抗驱动和涡流控制等方面取得了新的进展[7]。科研人员据此开发出了多款BCF模式推进的仿生机器鱼[4-12],同时针对游动效率、水动力学特性等进行了大量实验研究[14-16]。在MPF仿生机器鱼研究中,Blake等人[17]研究了其游动机理,提出了胸鳍摆动过程中的受力分析方法,Dickinson等人[18]关于昆虫空气动力学的研究结果也为鱼类胸鳍动力学行为分析提供了借鉴。Lauder等人[19-20]进一步研究了胸鳍形状、柔性等对MPF鱼类游动的影响,发展了Blake课题组的分析方法。以此为基础,人们相继开发了多款多鳍拍动式、胸鳍扑翼滑翔式和长鳍波动式仿生MPF机器鱼[1-2,21-34]。
多鳍拍动式仿生机器鱼多以两鳍推进或四鳍推进为主,具有良好的机动性和原地悬停能力,可实现沉浮、加速、转弯、翻滚等功能。其中两鳍推进机器鱼中,日本Kato教授[28-29]设计了一款两鳍推进仿生黑鲈鱼,其单侧胸鳍具有摇翼和前后拍翼两个自由度,在低速下具有良好的机动性和运动稳定性,其游速可达到0.05 m/s。北京大学研制了一款单自由度两鳍自主仿生机器鱼,可实现直线游动、转弯、沉浮等运动[9]。瑞士洛桑联邦理工学院研制的机器鱼BoxyBot,具有一对单自由度胸鳍和一个尾鳍,实现了直线游动、转弯、沉浮等运动[30]。华盛顿大学也设计了推进机构和功能与BoxyBot相似的一款仿生箱鲀[31]。这两款机器鱼类似于北京大学[9]所设计的自主仿生箱鲀,均是通过两侧胸鳍的摇翼运动、拍翼运动、或两者复合运动实现其基本游动模态。此外,美国特拉华大学Deng课题组研制了一种具有二自由度胸鳍和尾鳍的仿生机器鱼,并通过实验研究获得了最优尾鳍形状,与Kato教授的工作相比,其二自由度胸鳍是通过划水模式实现推进,通过数值仿真研究了不同鱼体外形对箱鲀鱼稳定性的影响,所研制机器鱼平均速度为0.041 1 m/s,转弯半径接近于0,但未对2自由度胸鳍的动力学行为进行分析[32-33]。兰州交通大学研制了一种“划水模式”推进的仿生箱鲀[34]。中科院自动化研究所设计的一款仿生白斑狗鱼,能够通过胸鳍的上下拍翼运动和摇翼运动,以及柔性身体的摆动实现推进[35]。
由上可知,目前以胸鳍/尾鳍协同推进的仿生机器鱼研究较少。为提高游动性能,有必要设计兼具BCF模式鱼类快速高效特点及MPF鱼类高机动性的仿生推进机构。为此,本文拟设计一种具有前后拍翼运动和摇翼运动胸鳍、尾鳍摆动以及以上三者运动复合的协同推进机构,并对其协同推进直线游动机理进行分析。
1 仿生机构设计
研究表明,鱼类的胸鳍运动形式包括(a)前后拍翼运动;(b)旋转式运动,即摇翼运动;(c)上下拍翼运动,如图1所示。
图中,以(a)和(b)复合运动推进称为阻力模式,以(b)和(c)复合运动推进称为升力模式。Webb通过实验研究发现,阻力模式在低速游动时效率较高,升力模式在高速游动时效率较高[36]。

图1 胸鳍三种基本运动示意图Fig.1 Three basic motion of pectoral fin
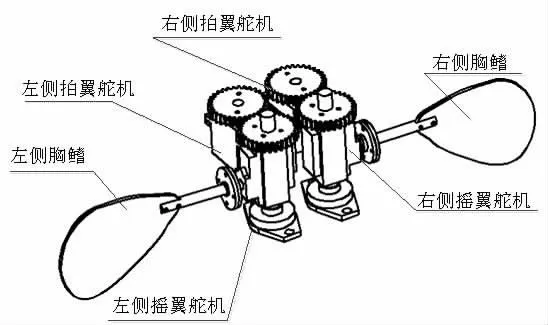
图2 仿生机器鱼胸鳍推进机构原理图Fig.2 Schematic diagram of pectoral fin in propulsion mechanism
本文以鳕鱼为仿生对象,设计了一种以阻力模式推进且沿鱼体轴线左右对称布置的二自由度胸鳍机构,如图2所示。其中,单侧胸鳍的前后拍翼运动由拍翼舵机转动通过齿轮副的传递实现;摇翼运动由摇翼舵机的转动直接输出。由于摇翼舵机的舵机支架固定在拍翼运动的传动链上,从而实现了摇翼运动与拍翼运动的分离。当同侧摇翼舵机与拍翼舵机同时输出时,即可实现阻力模式的推进。
所设计仿生鳕鱼的三关节柔性身体机构借鉴了北京大学的“游龙”机器鱼,柔性身体的蒙皮采用橡胶[8],鱼体前部壳体根据科鱼类的流线型设计,鱼体相关技术参数见表1。其中,样机外壳由PLA材料经3D打印加工而成,胸鳍由若干柔性碳棒作为鳍条,热缩蒙皮作为鳍面组成,所设计机器鱼样机如图3所示。

表1 仿生鳕鱼相关技术参数Tab.1 Related technical parameters of bionic cod

图3 仿生鳕鱼整体设计与实体图Fig.3 Overall design and entity diagram of bionic cod
2 仿生推进机构运动学建模
所设计仿生鳕鱼可通过以下几种方式进行游动。一是通过两侧胸鳍前后拍翼运动与摇翼运动的复合运动,以阻力模式进行推进;二是可通过两侧胸鳍的摇翼运动,以升力模式产生推进;三是通过柔性身体与尾鳍的摆动实现推进;最后,可通过胸鳍/尾鳍的协同运动实现推进。本节首先确定二自由度胸鳍以及尾鳍的运动规律,进而对其进行水动力学分析。
2.1 胸鳍复合模式和摇翼模式推进机构运动学建模
由本小节建立仿生机器鱼以第1种和第2种方式推进的运动学模型。研究表明,当机器鱼以阻力模式推进时,胸鳍通过鳍面与水面相垂直的后摆运动以及鳍面与水面相平行的回摆运动实现推进,因其类似于划水动作,故又称为“划水模式”,如图4所示。
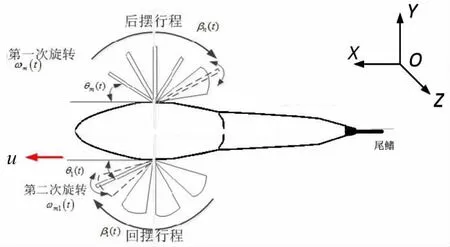
图4 胸鳍推进的后摆和回摆示意图Fig.4 Diagram of pectoral fin propulsion integrating back and forth swing
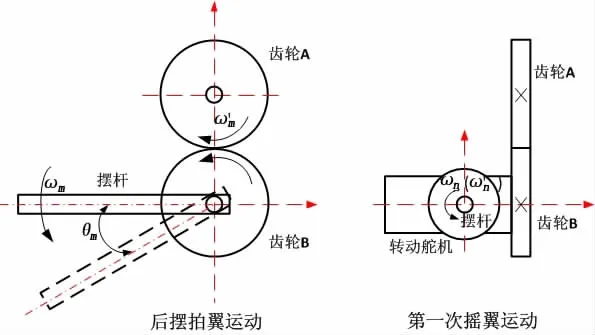
图5 机构运动示意图Fig.5 Schematic diagram of mechanism movement
以左侧胸鳍为例,其摇翼运动与拍翼运动如图5所示,其中θm为胸鳍后摆拍翼角,ωm为胸鳍后摆拍翼角速度,ωn为胸鳍第一次旋转摇翼角速度,ωm′为拍翼电机角速度,ωn′为摇翼电机角速度。易知,ωm=ωm′,ωn=ωn′。
为了实现仿生机器鱼稳定、高效的推进,胸鳍摆动应类似于正弦运动,以此为依据确定胸鳍摆动规律。由图4可知,所设计机器鱼的胸鳍运动可细分为四个阶段,如图6所示。其中,{X,Y,Z}为全局坐标系;{x,y,z}为随体坐标系,其中x轴指向鱼尾,y轴指向鱼体右侧,z轴指向机器鱼顶部。
如图6所示,θm为胸鳍后摆角,βn为第一次旋转角,θ1为胸鳍回摆角,β1为第二次旋转角。设在推进过程中,胸鳍后摆和回摆时间相同,记为Tb;两次旋转时间也相同,记为Tr,取胸鳍摆动规律为
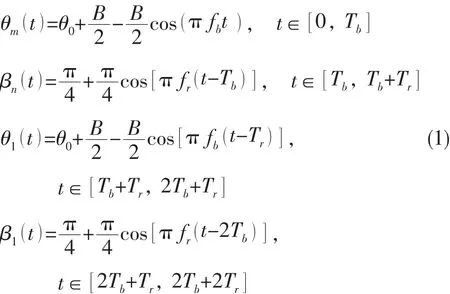
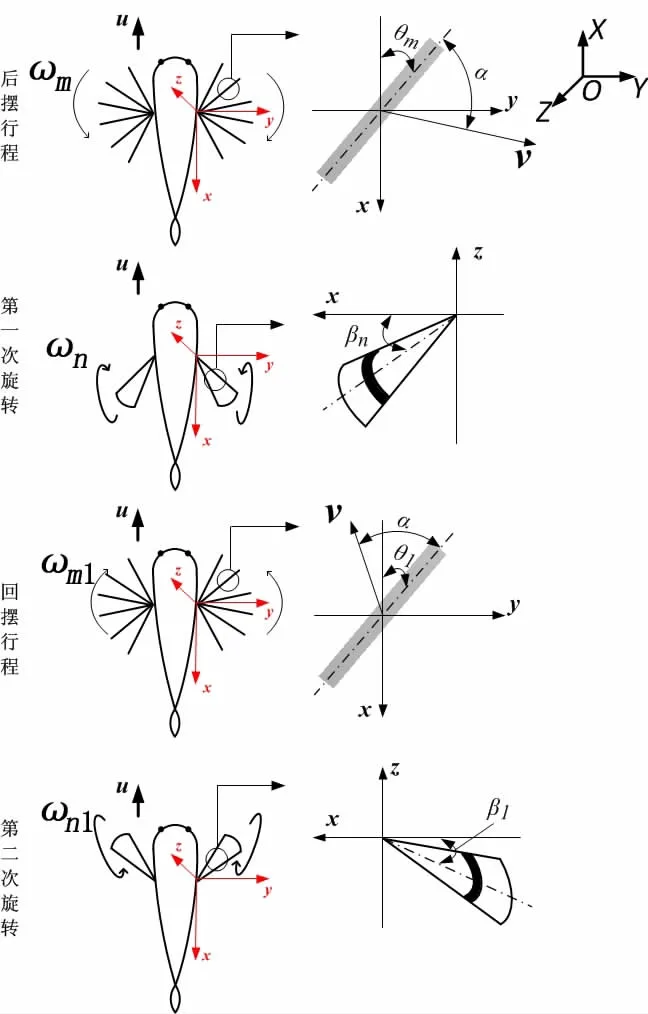
图6 仿生机器鱼胸鳍运动示意图Fig.6 Schematic diagram of pectoral fin movement
式中:θ0为回摆初始角位移,B为胸鳍回摆幅度,。对(1)式关于时间t求导,可得:

(1)式及(2)式给出了机器鱼在胸鳍前后拍翼运动及摇翼运动共同作用下推进的运动学方程。如前所述,通过两侧胸鳍的单自由度摇翼运动,仿生机器鱼也可实现推进。在此情形下,取胸鳍摇翼运动的规律为

式中:θy0为初始角,By为摇翼摆幅,fy为摇翼频率,φ为相位差,则摇翼运动的角速度为

2.2 尾鳍推进机构运动学建模
所设计仿生鳕鱼的三关节柔性身体/尾鳍也具有单独推进能力,亦可与胸鳍运动相配合,实现快速启动以及高速机动。受文献[5-6,8]启发,取鱼体轴线上刚性头部与柔性身体连接点为原点,取指向鱼尾方向为轴,指向鱼体右侧方向为,建立坐标系,如图7所示。令所设计机器鱼柔性身体/尾鳍按照Lighthill曲线摆动,其运动方程为
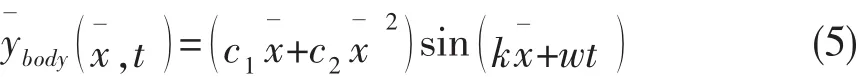
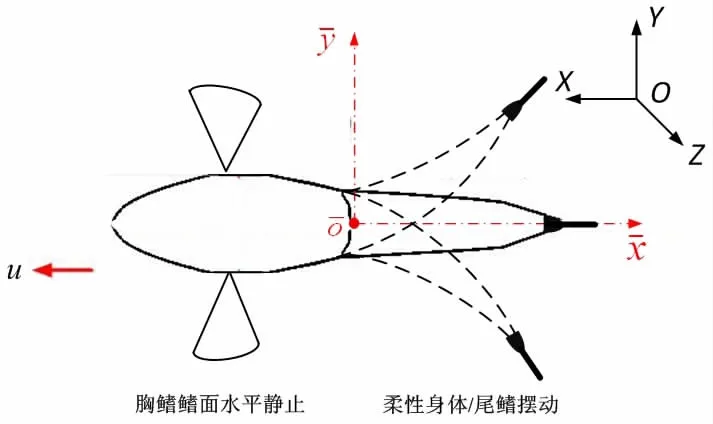
图7 仿生机器鱼尾鳍摆动示意图Fig.7 Schematic diagram of caudal fin movement
3 仿生机器鱼直线游动的动力学建模
3.1 双侧胸鳍拍翼/摇翼复合推进
由前可知,仿生机器鱼采用双侧胸鳍拍翼/摇翼复合推进时,后摆行程提供推进力,而回摆行程则产生阻力。由于胸鳍摆动时鳍面上不同位置具有不同的线速度,故采用“微元积分”方法对胸鳍在两个行程中的受力情况进行分析,即将扇形胸鳍沿展向分割为若干切片微元,对微元切片进行受力分析,最后通过沿展向积分获得整个胸鳍的受力。
以左侧胸鳍为例,首先分析后摆行程中的受力情况。任取鳍面上一微元P,其受力情况如图8所示。
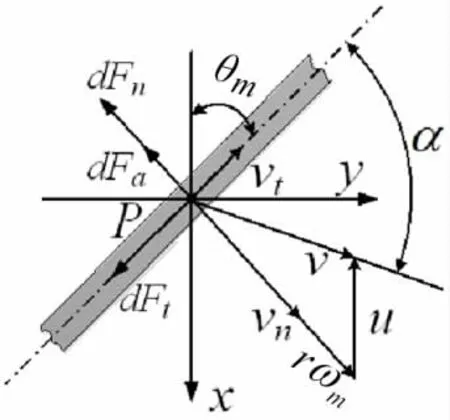
图8 机器鱼后摆行程中胸鳍微元P的受力分析Fig.8 Mechanical analysis of the element P of the pectoral fin in back swing
图中u为机器鱼沿x方向的游动速度,r为胸鳍的展向半径,α为相对来流速度v与胸鳍展向之间的夹角,称为水动力学攻角。易知,P处的法向速度vn和切向速度vt分别为

则周围流体作用于P上的法向升力dFn和切向阻力dFt分别为[17-18]

其中:ρ为流体密度,dA为微元P的面积,Cn为法向升力系数,Ct为切向阻力系数。设μ为流体粘性系数,δ为扇形胸鳍展开角,R为胸鳍外径,则有

由图8可知,微元P在x轴方向所受流体作用dFx为

则在后摆行程中,单侧胸鳍摆动产生的推进力为

当胸鳍后摆到极限位置时,胸鳍绕输出轴做摇翼运动,其旋转方向与后摆方向相一致,从而产生一定的推进力,其大小与胸鳍相对来流速度以及有效推力面积相关,受力情况如图9所示。其中,o-xyz为随体坐标系,O-XYZ为全局坐标系,u为机器鱼游速,Vx′为在x轴方向胸鳍相对流体速度。
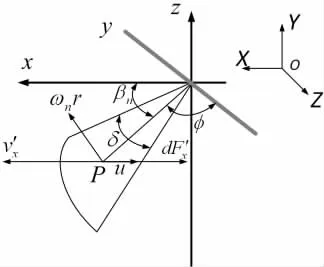
图9 机器鱼胸鳍第一次旋转受力分析Fig.9 Force analysis of the first rotation of the pectoral fin
设φ为胸鳍鳍面与y轴的夹角,则胸鳍微元P在x方向的有效推力面积dAd为

其中:φ=θm-π/2。胸鳍微元P相对流体在x轴方向的运动速度为

则流体在x方向作用于胸鳍微元P的推力dFx′为

其中:Cd是和雷诺数成反比的阻力系数,其大小为
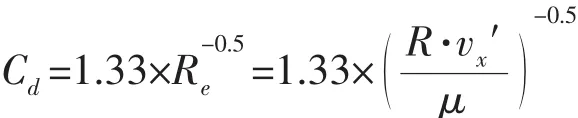
对(13)式沿鳍面展长进行积分,可得第一次旋转时单胸鳍沿x轴方向产生的推进力为

当胸鳍鳍面与水面相平行时,胸鳍开始做回摆运动。由于胸鳍与水平面保持平行,所以胸鳍受到的阻力可忽略不计,鱼体主要受到形体阻力D的作用,其大小与身体形状、表面粗糙度以及周围流场的流动状态有关,通过将机器鱼近似为长、宽、高分别为L,W,H的长方体,可得形体阻力D为[17]

为阻力系数。


则流体在x方向作用于胸鳍微元P的推力dFx″为
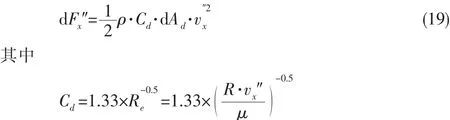
则单侧胸鳍在第二次摇翼运动中沿x轴方向所产生的阻力大小为

此外,机器鱼还受到流体附加质量力的作用,这是由于两侧胸鳍的非匀速摆动使得胸鳍微元切片夹带部分流体而产生的。由于在回摆行程中,胸鳍鳍面与水面平行,鱼体所夹带的附加流体质量较小,由其产生的流体附加质量力可以忽略不计。因此,仅考虑后摆行程所产生的流体附加质量力。设在此过程中胸鳍微元P处所夹带的流体附加质量为dma,则有

式中:c=δ·r为切片弦长,l=dr为切片展向长度。由文献[17-18]可知,由dma所产生的流体附加质量力dFa为

由图8可知,dFa在x轴方向的分量dFxa为

由于机器鱼在直线游动中,两侧胸鳍按相同规律做同步运动,因此在y轴方向合力为零,则由(10)、(14)、(15)、(20)式和(24)式可得其在x轴方向的动力学方程为
此外,农牧民群众对于小型农田水利工程的养护管理重视程度不足,不能做到很好的维护,出现问题之后无人问及,导致农田水利工程损伤范围越来越大,严重的导致农田水利工程废弃不能利用,对灌溉技术的推广应用产生影响。

3.2 双侧胸鳍摇翼运动推进
除采用胸鳍摇翼/前后拍翼复合运动实现推进外,所设计仿生鳕鱼还可以通过两侧胸鳍的单自由度摇翼运动,以升力模式实现推进。在此情形下,机器鱼主要受到流体沿鱼体中轴线方向对鳍面推进力Fxy,鳍面在摇翼运动过程中所夹带流体的附加质量力Fay,以及形体阻力Dy(Dy=D)的作用,胸鳍微元P处的受力情况与图8所示类似,不同之处为后摆角θm由摇翼角θy所代替。则由前述分析易知,单侧胸鳍微元P处所受法向升力dFn和切向力dFt分别为

由于两侧胸鳍所产生的切向力为一对平衡力,因此微元P处沿x轴所受推进力为

同理可得微元P所受流体附加质量力为:

其在机器鱼x轴方向的分力为

将(27)式及(29)式沿胸鳍展向积分可得单侧胸鳍的推力Fxy、附加质量力Fay分别为

则由(30)式和(15)式可得双侧胸鳍摇翼运动推进时机器鱼在x轴方向的动力学方程为

3.3 柔性身体/尾鳍推进
所设计仿生鳕鱼还可通过三关节柔性身体以及尾鳍的摆动,以BCF模式进行推进。受文献[5-8,41]启发,鱼体尾部关节按照(5)式所示Lighthill方程摆动,所产生的平推推力为

其中:bt是鱼体尾端半展长,at是振幅,ω为摆动频率,u为机器鱼游速,k为鱼体波数,有k=2π/λ,其中λ为鱼体波长,c为相速度,且有c=ω/k。设Tx=1/ω为摆动周期,则由(32)式可得

以上分析表明,所设计仿生鳕鱼能以多种形式实现直线游动,其动力学方程式(25)、(31),以及(33)式可以统一表示为
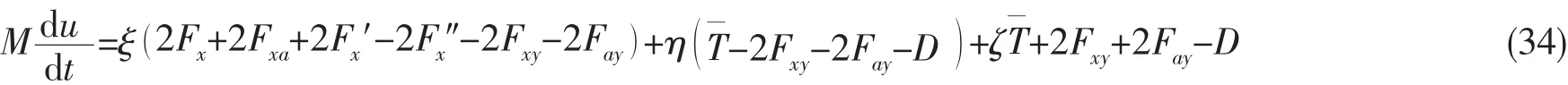
其中:ξ,η,ζ∈{0,1 },易知,当ξ=η=ζ=0时,机器鱼在胸鳍摇翼模式下游动;当ξ=1,η=ζ=0时,机器鱼在胸鳍复合模式下游动;当η=1,ξ=ζ=0时,机器鱼在尾鳍推进模式下游动;当η=0,ξ=ζ=1时,机器鱼在胸鳍复合与尾鳍协同推进模式下游动;当ζ=1,η=ξ=0时,机器鱼在胸鳍摇翼与尾鳍协同推进模式下游动。
4 仿生机器鱼直线游动特性分析
本章以(34)式为基础,对所设计仿生鳕鱼的直线游动特性进行数值分析,为实体实验提供依据。
当ξ=1,η=ζ=0时,机器鱼在胸鳍复合模式下游动,其运动参数初值由表2给出,仿真结果如图11-12所示。由图11可知,在第2个周期,游速达到稳态,最高峰值为0.23 m/s,平均游速为0.17 m/s。由图12可知,在胸鳍摆幅小于50°时,机器鱼游速与摆幅成正比,在50°以后,机器鱼游速达到稳态;胸鳍周期与游速成反比,并在胸鳍摆动周期为0.5 s时,游速达到最大值为0.27 m/s。
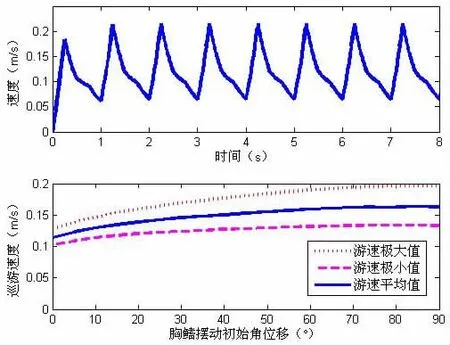
图11 胸鳍初始角对胸鳍复合推进时游速的影响Fig.11 Effect of initial angle of pectoral fins on composite propulsion
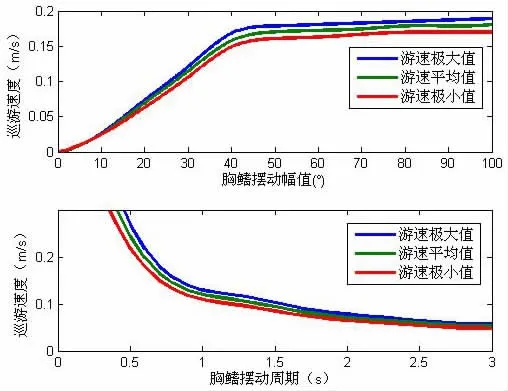
图12 胸鳍摆幅和周期对胸鳍复合推进游速的影响Fig.12 Effect of swing amplitude and cycle of pectoral fins on composite propulsion

表2 胸鳍复合模式运动参数初值Tab.2 Initial value of motion parameters in pectoral fins composite motion
当ξ=η=ζ=0时,机器鱼在胸鳍摇翼模式下游动,其运动参数初值由表3给出,仿真结果如图13-14所示。由图13可知,在第2个周期,游速达到稳态,最高峰值为0.068 m/s,平均游速为0.038 m/s。由图14可知,在胸鳍摆幅小于75°时,机器鱼游速与摆幅成正比,在75°以后,机器鱼游速达到稳态;胸鳍摆动周期Ty与游速成反比,当Ty=2 s时,游速趋于稳定,其值为0.035 m/s。

表3 胸鳍摇翼推进模式运动参数初值Tab.3 Initial value of motion parameters in pectoral fins’swaying motion
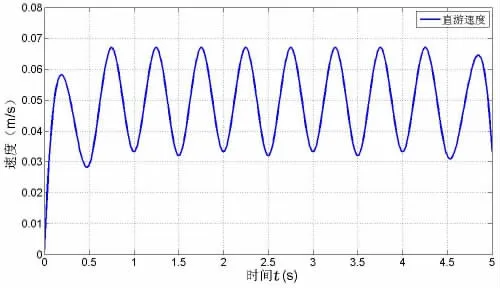
图13 胸鳍摇翼推进时的直线游动速度Fig.13 Straight swimming speed in pectoral fins’swaying motion
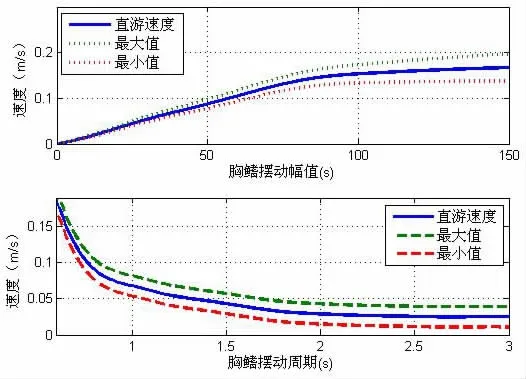
图14 胸鳍摆动周期和摆幅对摇翼推进游速的影响Fig.14 Effect of swing amplitude and cycle in pectoral fins’swaying motion
当η=1,ξ=ζ=0时,机器鱼在尾鳍推进模式下游动,其运动参数初值由表4给出,仿真结果如图15-16所示。由图15可知,其游速在第3个运动周期达到均值,最高峰值为0.25 m/s,平均游速约为0.22 m/s,且游速与摆动频率成正比。由图16可知,机器鱼的游速与尾鳍摆动频率成正比,即机器鱼直线游速随尾鳍摆动频率的增加而增大。

图15 尾鳍推进时的直线游动速度Fig.15 Straight swimming speed in only caudal fin movement
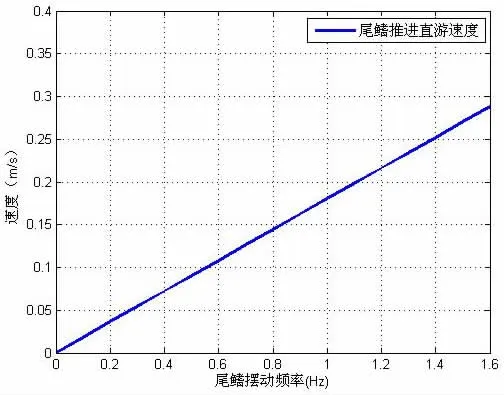
图16 尾鳍摆动频率对游速的影响Fig.16 Effect of swing frequency in only caudal fin movement
当η=0,ξ=ζ=1时,机器鱼在双侧胸鳍与尾鳍协同推进模式下游动,其中胸鳍采用复合运动模式,其运动参数初值由表2和表4给出。由图17可知,复合推进下的速度波动较单独双胸鳍推进时的速度波动小,速度值增大,其中均值达0.25 m/s,最高峰值为0.30 m/s。

表4 尾鳍推进模式运动参数初值Tab.4 Initial value of motion parameters in only caudal fin movement
当ζ=1,η=ξ=0时,机器鱼在双侧胸鳍与尾鳍协同推进模式下游动,其中胸鳍采用摇翼运动模式,其运动参数初值由表3和表4给出。由图18可知,其游动速度均值为0.20 m/s,峰值为0.23 m/s。对比图15和图18可知,胸鳍采用摇翼模式时的胸尾鳍协同推进运动的平均游速和峰值游速均小于尾鳍单独推进时的平均游速和峰值游速,出现该结果的可能原因是由于在胸尾鳍协同推进过程中,胸鳍产生的推进行波与尾鳍产生的波相互耦合作用,对整个鱼体前进起到阻碍的作用。

图17 双胸鳍复合与尾鳍协同推进直线游速与时间的关系Fig.17 Relations between straight swimming speed and times in the propulsion of pectoral fins composition with caudal fin
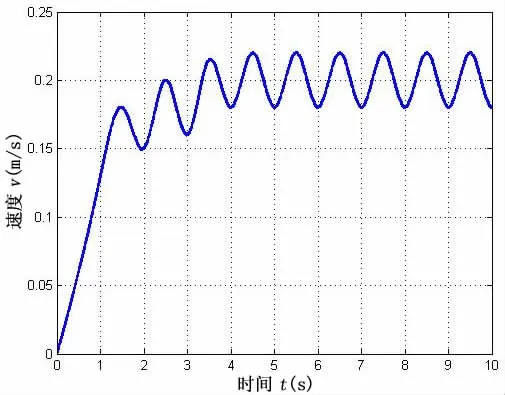
图18 双胸鳍摇翼与尾鳍协同推进直线游速与时间的关系Fig.18 Relations between straight swimming speed and times in the propulsion of pectoral fins’swaying with caudal fin
5 实 验
本章通过实体实验对理论分析结果进行验证,实验环境由室内鱼池环境更换为人工湖平静水面,最大限度减少壁面回波及自然风等对实验结果的干扰,具体实验环境如图19所示。实验中机器鱼运动学参数初值分别由表2、表3和表4给出,胸鳍和尾鳍分别按照按(1)、(3)式和(5)式给定的运动规律摆动,机器鱼的运动姿态利用高清摄像机以及湖底标记尺进行采集,最后通过图像处理得到位姿数据。

图19 机器鱼实验环境Fig.19 Experimental environment of the bionic cod
图20-21所示为双侧胸鳍复合推进模式下的直游实验结果,由图21可知,机器鱼直游速度约为0.15 m/s,与图11所示仿真结果基本一致;图22-23所示为双侧胸鳍摇翼模式推进下的直游实验结果,由图23可知其直游速度约为0.05 m/s,与图13仿真结果基本一致;图24-25为尾鳍推进模式下的直线游动实验结果,由图25可知其游动速度为0.18 m/s,与图15的仿真结果基本一致。
由上述实验结果可知,胸鳍复合推进模式的直线游速明显高于胸鳍摇翼模式,虽然这两种推进模式下的游动速度均小于尾鳍单独推进时的直线游速,但是其游动姿态比后者更稳定,适合于仿生机器鱼低速游动的情形。

图20 双侧胸鳍复合推进模式下直游实验Fig.20 Straight swimming experiments of pectoral fins composite propulsion
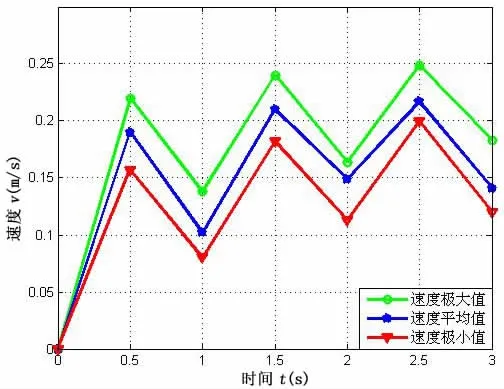
图21 双胸鳍复合直线游速Fig.21 Straight swimming speed of pectoral fins composite propulsion

图22 双侧胸鳍摇翼模式下直游实验Fig.22 Straight swimming experiments of pectoral fins’swaying motion
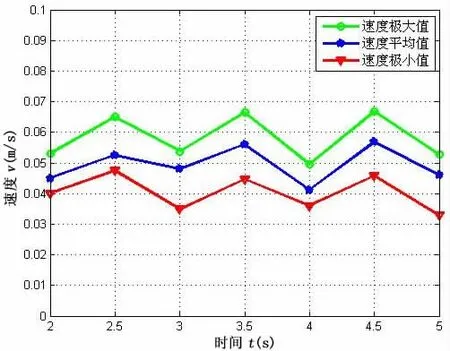
图23 双侧胸鳍摇翼直线游速Fig.23 Straight swimming speed of pectoral fins’swaying motion

图24 三关节尾鳍模式下直游实验Fig.24 Straight swimming experiments of caudal fin propulsion
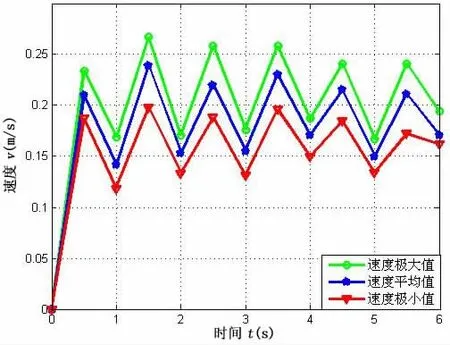
图25 三关节尾鳍直线游速Fig.25 Straight swimming speed of caudal fin propulsion

图26 双侧胸鳍复合与三关节尾鳍协同推进模式下直游实验Fig.26 Straight swimming experiments of integrating pectoral fins composition with caudal fin
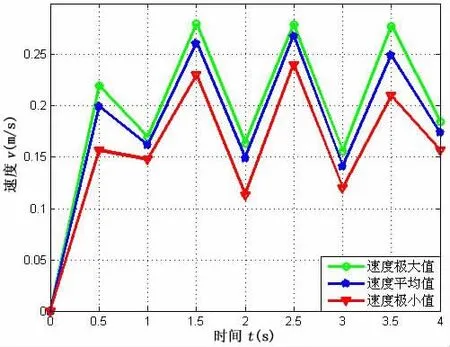
图27 双侧胸鳍复合与尾鳍协同推进直线游速Fig.27 Straight swimming speed of integrating pectoral fins composition with caudal fin

图28 双侧胸鳍摇翼与三关节尾鳍协同推进模式直游实验Fig.28 Straight swimming experiments of integrating pectoral fins’swaying with caudal fin
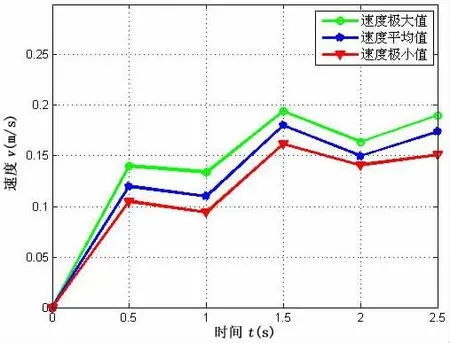
图29 双侧胸鳍摇翼与尾鳍协同推进直线游速Fig.29 Straight swimming speed of integrating pectoral fins’swaying with caudal fin
图26-27为所设计仿生鳕鱼在双侧胸鳍复合运动与柔性身体摆动协同推进时的直游实验结果。由图27可知,其游速约为0.22 m/s,这与图17的仿真结果相一致;图28-29为双胸鳍摇翼运动与尾鳍协同推进时的直游实验结果,由图29可知其游速约为0.16 m/s,与图18的仿真结果基本一致。
双侧胸鳍复合/尾鳍协同推进实验结果表明,其直线游速高于单独柔性身体/尾鳍推进时的游速,表明通过胸鳍协同推进可获得更高的游速,且能够明显提高机器鱼游动的稳定性和机动性。
双侧胸鳍摇翼/尾鳍协同推进实验结果表明,其直线游速略低于单独柔性身体/尾鳍推进时的游速,且图25和图29的对比结果与图18和图15的仿真对比结果相同,说明胸尾鳍协同推进直游过程中,胸尾鳍的耦合叠加作用对鱼体游速起正向推进或反向阻碍作用。
6 结 论
本文以鳕鱼为仿生对象,设计了一种二自由度胸鳍/尾鳍协同推进的仿生机器鱼,分别分析了胸鳍摇翼运动、拍翼运动、尾鳍摆动单独推进、以及三者复合推进时的直线游动性能。研究结果表明,仿生机器鱼在胸鳍/尾鳍系统协同推进时游速可达0.30 m/s,高于尾鳍单独推进时的游速;在胸鳍摇翼运动推进模式下,在最低游速为0.05 m/s条件下,仿生机器鱼也能实现稳定的游动。由此可见,所设计仿生鳕鱼的直线游动模态多样,且稳定游动的游速选择范围较宽,从而为直线游动模态的划分和确定提供了较大的灵活度。同时,该仿生机器鱼在游动过程中,可通过胸鳍与水面相垂直的方式实现停车,因此具有较高的机动性;且可通过胸鳍单独推进实现倒游,从而具有更好的环境适应能力。在后续工作中,将从两个方向深入。一方面是运用CPG控制模型和CFD模流分析,对胸尾鳍叠加作用做进一步精确控制和机理研究,另一方面将从研究机器鱼倒游、翻滚、以及胸鳍/尾鳍协同推进转弯等行为的游动机理和控制方法方面展开。
[1]蔡月日,毕树生.胸鳍摆动推进模式仿生鱼研究进展[J].机械工程学报,2011,47(19):30-37. Cai Yueri,Bi Shusheng.Research advances of bionic fish propelled by oscillating paired pectoral foils[J].Journal of Mechanical Engineering,2011,47(19):30-37.
[2]王田苗,杨兴帮,梁建宏.中央鳍/对鳍推进模式仿生自主水下机器人发展现状综述[J].机器人,2013,35(3):352-384. Wang Tianmiao,Yang Xingbang,Liang Jianhong.A survey on bionic autonomous underwater vehicles propelled by median and/or paired fin mode[J].Robot,2013,35(3):352-384.
[3]杨清海,喻俊志,谭 民,王 硕.两栖仿生机器人研究综述[J].机器人,2007,29(6):601-608. Yang Haiqing,Yu Junzhi,Tan Min,Wang Shuo.Amphibious biomimetic robots:A review[J].Robot,2007,29(6):601-608.
[4]魏清平,王 硕,谭 民,王 宇.仿生机器鱼研究的进展与分析[J].系统科学与数学,2012,32(10):1274-1286. Wei Qingping,Wang Shuo,Tan Min,Wang Yu.Research development and analysis of biomimetic robotic fish[J].Journal of Systems Science and Mathematical Sciences,2012,32(10):1274-1286.
[5]Lighthill J.Mathematical biofluid dynamics[J].Society for Industrial Applied Mathematics Philadelphia Pa,1975,386(4): 1-3.
[6]童秉纲,庄礼贤,程健宇.鱼类波状摆动推进的流体力学研究[J].力学与实践,1991(3):17-26. Tong Binggang,et al.Hydrodynamics study on the wave propulsion of fish[J].Mechanics in Engineering,1991(3):17-26.
[7]崔 祚,姜洪洲,何景峰,等.BCF仿生鱼游动机理的研究进展及关键技术分析[J].机械工程学报,2015(16):177-184. Cui Zuo,Jiang Hongzhou,He Jingfeng,et al.Research development and key techniques of bcf robotic fish in locomotion mechanism[J].Journal of Mechanical Engineering,2015(16):177-184.
[8]Shao J,Wang L,Yu J.Development of an artificial fish-like robot and its application in cooperative transportation[J]. Control Engineering Practice,2008,16(5):569-584.
[9]Hu Y H,Zhao W,Xie G M,et al.Development and target following of vision-based autonomous robotic fish[J].Robotica, 2009,27:1075-1089.
[10]Wang W,Xie G.CPG-based locomotion controller design for a boxfish-like robot[J].International Journal of Advanced Robotic Systems,2014,11(87):147-169.
[11]Yan Q,Han Z,Zhang S W,et al.Parametric research of experiments on a carangiform robotic fish[J].Journal of Bionic Engineering,2008,5(2):95-101.
[12]韩 珍,颜 钦,张世武,等.基于序列图像处理法的机器鱼转向机动性能研究[J].机器人,2010,32(5):586-591. Han Zhen,Yan Qin,Zhang Shiwu,et al.Study on turning maneuverability of robot fish with sequential image processing [J].Robot,2010,32(5):586-591.
[13]Wen L,Wang T M,Wu G H,et al.Quantitative thrust efficiency of a self-propulsive robotic fish:experimental method and hydrodynamic investigation[J].IEEE/ASME Transactions on Mechatronics,2013,18(3):1027-1038.
[14]夏 丹,陈维山,伍志军,等.科模式机器鱼自主游动的水动力特性研究[J].机械工程学报,2013,49(21):54-61. Xia Dan,Chen Weishan,Wu Zhijun,et al.Research on hydrodynamics of carangiform mode robotic fish swimming under self-propulsion[J].Journal of Mechanical Engineering,2013,49(21):54-61.
[15]陈维山,夏 丹,刘军考,等.尾鳍运动行为对仿鱼机器人稳态游动性能的影响[J].机械工程学报,2011,3:1-7. Chen Weishan,Xia Dan,Liu Junkao,et al.Effect of kinematic behavior of caudal fin on fishlike robot propulsion during steady swimming[J].Journal of Mechanical Engineering,2011,3:1-7.
[16]夏 丹,陈维山,刘军考,等.仿生机器鱼自主游动中的流体结构耦合新方法[J].机械工程学报,2014,50(7):15-22. Xia Dan,Chen Weishan,Liu Junkao,et al.New method of fluid-structure coupling in self-propelled swimming[J].Journal of Mechanical Engineering,2014,50(7):15-22.
[17]Blake R W.The mechanics of labriform locomotion:An analysis of the recovery stroke and the overall fin beat cycle propulsive efficiency in the angelfish[J].Journal of Experimental Biology,1979,82(1):337-342.
[18]Dickinson M H,Lehmann F O,Sane S P.Wing rotation and the aerodynamic basis of insect flight.[J].Science,1999,284 (5422):1954-60.
[19]Borazjani I,Blevins E L,Lauder G V.Hydrodynamics of swimming in stingrays:numerical simulations and the role of the leading-edge vortex[J].Journal of Fluid Mechanics,2016,788(Pt 13):407-443.
[20]Tangorra J,Davidson S,Hunter N,et al.The development of a biologically inspired propulsor for unmanned underwater vehicles[J].IEEE Journal of Oceanic Engineering,2007,32(3):533-550.
[21]Zhou C,Low K H.Design and locomotion control of a biomimetic underwater vehicle with fin propulsion[J].IEEE/ASME Transactions on Mechatronics,2012,17(1):25-35.
[22]Low K H.Modelling and parametric study of modular undulating fin rays for fish robots[J].Mechanism&Machine Theory,2009,44(3):615-632.
[23]Low K H,Zhong C Z Y.Gait planning for steady swimming control of biomimetic fish robots[J].Advanced Robotics, 2009,23(7-8):805-829.
[24]Zhou H,Hu T,Low K H,et al.Bio-inspired flow sensing and prediction for fish-like undulating locomotion:A CFD-aided approach[J].Journal of Bionic Engineering,2015,12(3):406-417.
[25]Ma H W,Cai Y R,Wang Y L,Bi S S,Zhao G.Abiomimetic cownose ray robot fish with oscillating and chordwise twisting flexible pectoral fins[J].International Journal of Industrial Robot,2015,42(3):214-221.
[26]章永华,何建慧,贾来兵.仿生蓝点魟胸鳍在两种波动模式下推进力的比较[J].机械工程学报,2012,48(18):166-176. Zhang Yonghua,He Jianhui,Jia Laibing.Comparative analysis of thrust generation of biomimetic bluespotted[J].Journal of Mechanical Engineering,2012,48(18):166-176.
[27]牛传猛,毕树生,蔡月日,等.胸鳍摆动推进仿生鱼的设计及水动力实验[J].机器人,2014(5):535-543. Niu Chuanmeng,Bi Shusheng,Cai Yuesheng,et al.Design and hydrodynamic experiments on bionic robotic fish with oscillating pectoral fins[J].Robot,2014,36(5):535-543.
[28]Kato N,Furushima M.Pectoral fin model for maneuver of underwater vehicles[C].Proceedings of the 1996 Symposium on Autonomous Underwater Vehicle Technology,1996.AUV’96,1996:49-56.
[29]Kato N.Median and paired fin controllers for biomimetic marine vehicles[J].Journal of Applied Mechanics Review,2005, 58:238-252.
[30]Crespi A,Lachat D,Pasquier A,et al.Controlling swimming and crawling in a fish robot using a central pattern generator [J].Autonomous Robots,2008,25(1-2):3-13.
[31]Morgansen K A,Triplett B I,Klein D J.Geometric methods for modeling and control of free-swimming fin-actuated underwater vehicles[J].IEEE Transactions on Robotics,2007,23(6):1184-1199.
[32]Kodati P,Hinkle J,Winn A,et al.Microautonomous Robotic Ostraciiform(MARCO):Hydrodynamics,design,and fabrication[J].IEEE Transactions on Robotics,2008,24(1):105-117.
[33]Barbera G,Pi L,Deng X.Attitude control for a pectoral fin actuated bio-inspired robotic fish[C].IEEE International Conference on Robotics&Automation,2011:526-531.
[34]李宗刚,毛著元,高 溥,等.一种2自由度胸鳍推进机构设计与动力学分析[J].机器人,2016(1):82-90. Li Z G,Mao Z Y,Gao P,et al.Design and dynamic analysis of pectoral-fin propelled mechanism with two degrees of freedom[J].Robot,2016,38(1):82-90.
[35]Zhengxing W U,Junzhi Y U,Zongshuai S U,et al.Towards an Esox lucius inspired multimodal robotic fish[J].Science China Information Sciences,2015,58(5):1-13.
[36]Webb P W.Kinematics of pectoral fin propulsion in Cymatogaster aggregata[J].J Exp.Biol,1973,59(3):697-710.
[37]Triantafyllou M S,Triantafyllou G S,Yue D K P.Hydrodynamics of fishlike swimming[J].Annu.rev.fluid Mech,2000,32 (1):33-53.
[38]Drucker E G,Lauder G V.Locomotor function of the dorsal finin teleost fishes:experimental analysis of wake forces in sun-fish[J].Journal of Experimental Biology,2001,204(204):2943-58.
[39]Triantafyllou M S,Triantafyllou G S.An efficient swimming machine[J].Scientific American,1995,272(3):64-70.
[40]Lighthill M J.Aquatic animal propulsion of high hydromechanical efficiency.J Fluid Mech 44:265-301[J].Journal of Fluid Mechanics,1970,44(2):265-301.
[41]童秉纲,庄礼贤.描述鱼类波状游动的流体力学模型及其应用[J].自然杂志,1998(1):1-7. Tong B G,Zhuang L X,Graduate school.hydrodynamic model for fish’s undulatory motion and its applications[J].Nature Magazine,1998(1):1-7.
[42]Yu J,Liu L,Wang L.Dynamic modeling and experimental validation of biomimetic robotic fish[C].American Control Conference,2006.IEEE,2006.
Dynamic modeling and experimental research on the linear swimming of a biomimetic cod fish driven by pectoral fin with two degrees of freedom and flexible body
LI Zong-gang,XU Wei-qiang,WANG Wen-bo,DU Ya-jiang
(School of Mechatronic Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)
Designing a novel biomimetic robotic Codfish in which namely driven by 2-DOF(degree of freedom)pectoral-fins and caudal fin,the pectoral fins can achieve flapping,swaying,the composite motion of them and collaborating locomotion with caudal fin,separately.And then,the straight swimming hydrodynamics model is established when fish is driven by bilateral pectoral fins,or by pectoral fins and caudal fin together.The numerical simulation and experimental results,show that the maximum velocity of straight swimming achieves at 0.30 m/s by pectoral fins and flexible body together,and the minimum velocity is 0.5 m/s by pectoral fins’swaying,other’s velocity of propulsion methods lie between the two cases,but are able to achieve a stable swimming.Compared with the existing results,the designed robotic fish have more abundant modes,wide speed range with better stability and better mobility.
bionic cod;pectoral-fins with two degrees of freedom;caudal fin; promote synergy;hydrodynamic analysis
TP24
:Adoi:10.3969/j.issn.1007-7294.2017.05.001
1007-7294(2017)05-0513-15
2017-02-16
国家自然科学基金资助项目(61663020,61064008);教育部科学技术研究重点项目(211185);甘肃省自然科学基金(1208RJZA166)
李宗刚(1975-),男,博士,教授,E-mail:lizongg@126.com.;徐卫强(1988-),男,硕士研究生;王文博(1986-),男,硕士研究生;杜亚江(1963-),男,教授。

